第6课时 复数的几何意义2
图片预览





文档简介
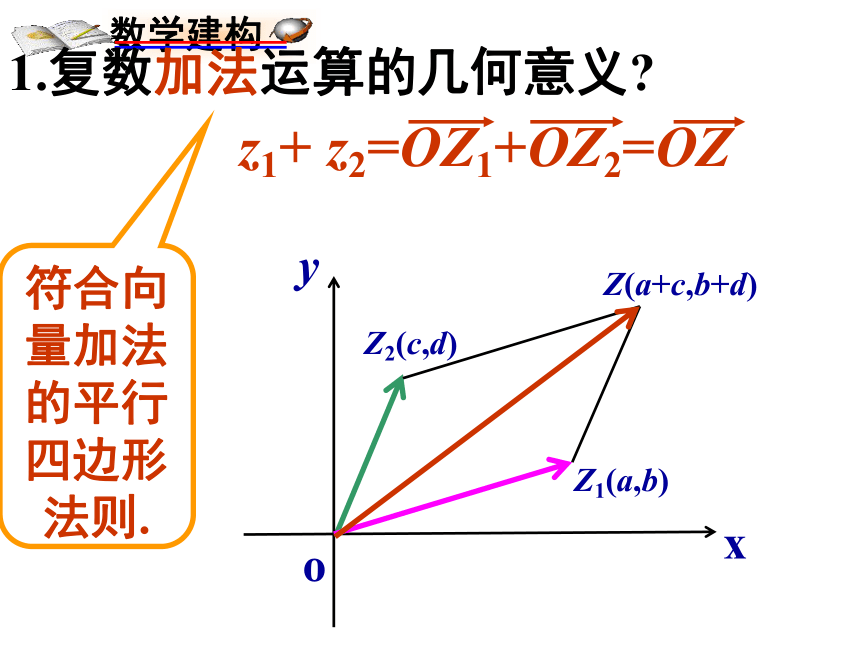
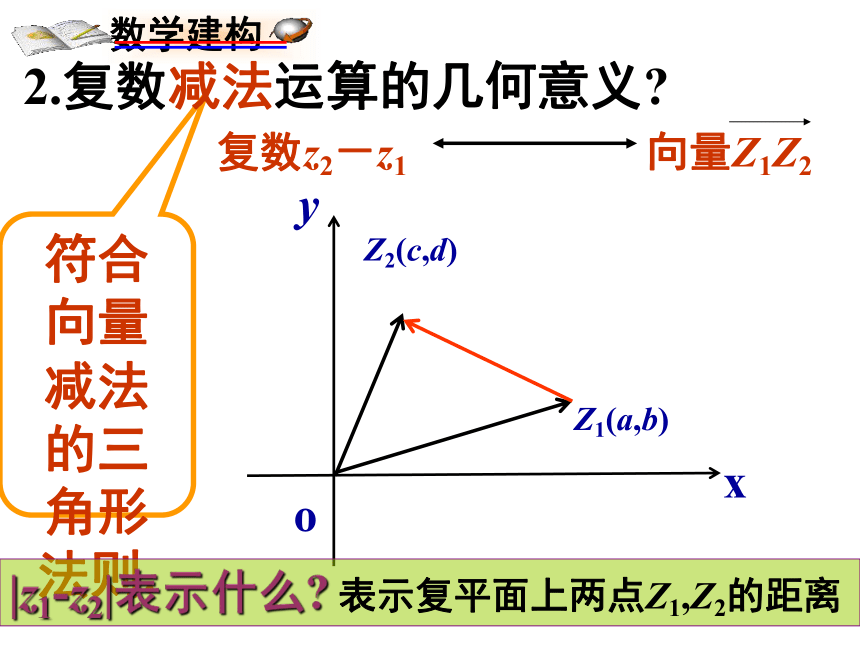
课件15张PPT。第84课时 复数的几何意义(2) 已知复数m=2-3i,若复数z满足等式|z-m|=1,则z所对应的点的集合是什么图形?xoyZ1(a,b)Z2(c,d)Z(a+c,b+d)z1+ z2=OZ1+OZ2=OZ符合向量加法的平行四边形法则.1.复数加法运算的几何意义?xoyZ1(a,b)Z2(c,d)符合向量减法的三角形法则.2.复数减法运算的几何意义?|z1-z2|表示什么?表示复平面上两点Z1,Z2的距离 已知复数z对应点A,说明下列各式所表示的几何意义.
(1)|z-(1+2i)|
(2)|z+(1+2i)|
(3)|z-1|
(4)|z+2i|例1.若复数z满足|z-3i|-|z+3i|=4,求 复数z在复平面内对应的点所对应的曲线. 变题1.若复数z满足|z-1|2-|z+i|2=4,求复数z在复平面内对应的点所对应的曲线. 变题2.若复平面上A,B两点分别对应 1和i,复数z在线段AB上移动,求z2对应点轨迹. 设复数z=x+yi,(x,y?R),在下列条
件下,求动点Z(x,y)的轨迹.
(1)|z-2|=1
(2)|z-i|+|z+i|=4
(3)|z-2|=|z+4|例2.若|z+1-i|=1,求|z|最大值和最小值. 例3.已知z1,z2?C,|z1|=|z2|=1,|z1+z2|= 求|z1-z2|. 例4.已知正方形ABCD的三个顶点坐标分别是A(1,2),B(-2,1),C(-1,-2),求D点的坐标. 练习:复数z1,z2分别对应复平面内的点M1,M2,且|z2+z1|= |z2-z1|,线段M1M2的中点M对应的复数为4+3i,求|z1|2+|z2|2.同学们.再见!xO设z=x+yi(x,y∈R)满足|z|=2(z?C)的复数z对应的点在复平面上将构成怎样的图形?22–2–2图形: 以原点为圆心,2为半径的圆上y5xy设z=x+yi(x,y∈R)满足2<|z|<3(z?C)的复数z对应的点在复平面上将构成怎样的图形?33–3–32–2–2图形:以原点为圆心,半径2至3的圆环内.O2
(1)|z-(1+2i)|
(2)|z+(1+2i)|
(3)|z-1|
(4)|z+2i|例1.若复数z满足|z-3i|-|z+3i|=4,求 复数z在复平面内对应的点所对应的曲线. 变题1.若复数z满足|z-1|2-|z+i|2=4,求复数z在复平面内对应的点所对应的曲线. 变题2.若复平面上A,B两点分别对应 1和i,复数z在线段AB上移动,求z2对应点轨迹. 设复数z=x+yi,(x,y?R),在下列条
件下,求动点Z(x,y)的轨迹.
(1)|z-2|=1
(2)|z-i|+|z+i|=4
(3)|z-2|=|z+4|例2.若|z+1-i|=1,求|z|最大值和最小值. 例3.已知z1,z2?C,|z1|=|z2|=1,|z1+z2|= 求|z1-z2|. 例4.已知正方形ABCD的三个顶点坐标分别是A(1,2),B(-2,1),C(-1,-2),求D点的坐标. 练习:复数z1,z2分别对应复平面内的点M1,M2,且|z2+z1|= |z2-z1|,线段M1M2的中点M对应的复数为4+3i,求|z1|2+|z2|2.同学们.再见!xO设z=x+yi(x,y∈R)满足|z|=2(z?C)的复数z对应的点在复平面上将构成怎样的图形?22–2–2图形: 以原点为圆心,2为半径的圆上y5xy设z=x+yi(x,y∈R)满足2<|z|<3(z?C)的复数z对应的点在复平面上将构成怎样的图形?33–3–32–2–2图形:以原点为圆心,半径2至3的圆环内.O2
