第1课时 合情推理
图片预览









文档简介
课件34张PPT。 创造过程是一个艰苦曲折的过程.数学家创造性的工作是论证推理,即证明.但这个证明是通过合情推理、通过猜想而发现的.——G.波利亚合情推理第86课时 合情推理 有一小贩在卖一篮杨梅,一顾客先尝了一个,觉得甜,又尝了一个,也是甜的,再尝了一个,还是甜的,所以他得出了一个结论:这一篮杨梅都是甜的! 这位顾客做了一个探索活动,这个活动是一个不断地提出猜想
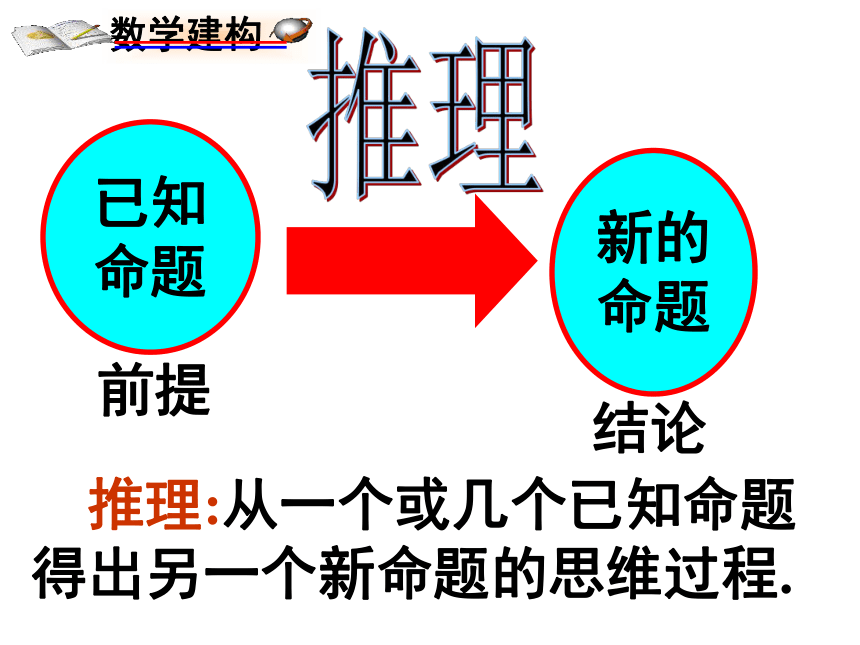
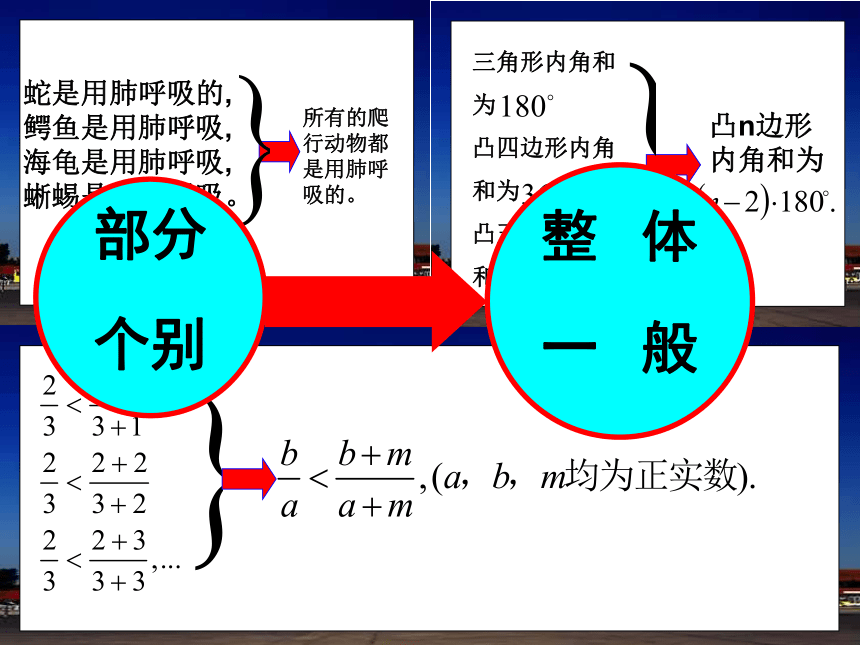
—验证猜想—再提出猜想—再验证猜想的过程。案例1:蛇是用肺呼吸的,鳄鱼是用肺呼吸的,海龟是用肺呼吸的,蜥蜴是用肺呼吸的.蛇、鳄鱼、海龟、蜥蜴都是爬行动物.由此猜想:案例2:三角形的内角和是1800,凸四边形的内角和是3600,凸五边形的内角和是5400,…由此猜想:所有的爬行动物都是用肺呼吸的.凸n边形的内角和是(n-2)×1800案例3:由此猜想:推理 推理:从一个或几个已知命题得出另一个新命题的思维过程.蛇是用肺呼吸的,鳄鱼是用肺呼吸,海龟是用肺呼吸,蜥蜴是用肺呼吸。所有的爬行动物都是用肺呼吸的。三角形内角和
为
凸四边形内角
和为
凸五边形内角
和为
凸n边形内角和为部分
个别整 体
一 般 从 中推演出
的推理,通
常称为归纳推理.个别事实一般性的结论观察下列等式
3+7=10,
3+17=20,
13+17=30,归纳出一个规律:
偶数=奇质数+奇质数
通过更多特例的检验,从6开始,没有出现反例.大胆猜想: 任何一个不小于6的偶数都等于两个奇质数的和.哥德巴赫猜想
10=3+7,
20=3+17,
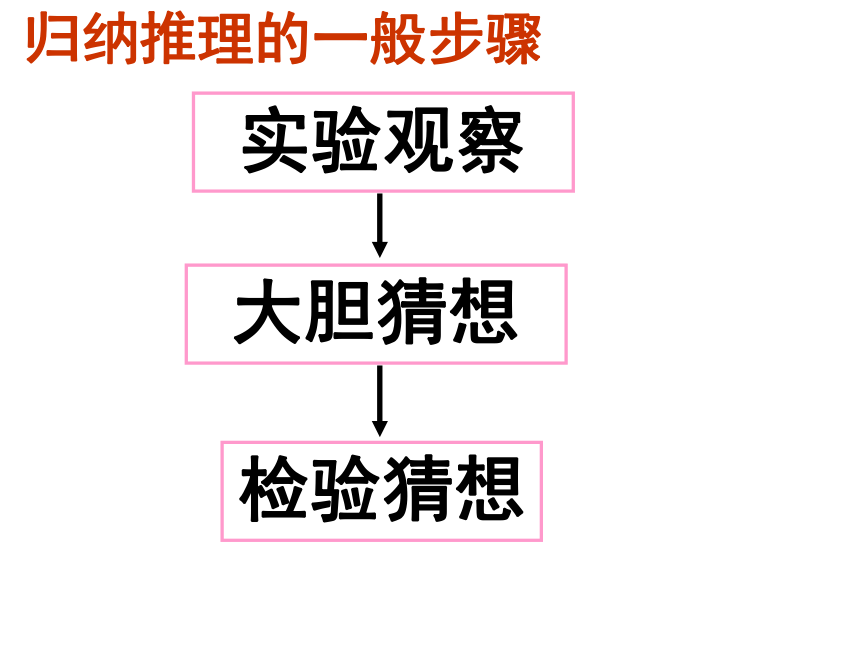
30=13+17.陈氏定理实验观察大胆猜想检验猜想归纳推理的一般步骤归纳推理的几个特点:1.归纳推理的前提是几个已知的特殊现象,归纳得出的结论是尚属未知的一般现象,该结论超越了前提所包容的范围.2.归纳推理得到的结论具有猜测的性质,结论是否真实,还需经过逻辑证明和实践检验.它不能作为数学证明的工具.3.归纳推理是一种具有创造性的推理.通过归纳推理得到的猜想,可以作为进一步研究的起点,帮助人们发现问题和提出问题.例1.已知数列{an}的每一项都是正数,且a1=1, ,试归纳出这个数列的一个通项公式.解.当n=1时,a1=1;当n=2时,a2=
当n=3时,a3= ;当n=4时,a4= .
……由此我们可以猜想出{an}的一个通项公式为 .1. 观察下列等式,并从中归纳出一般的结论:(1)1. 观察下列等式,并从中归纳出一般的结论:1-4+9-16+……+(-1)n+1×n2=(-1)n+1(1+2+3+……+n).例2.下面推理是归纳推理吗?所得结论正确吗?
(1)f(x)=(x-1)(x-2)…(x-100)+2,因为f(1)=2,f(2)=2,…f(100)=2,所以归纳猜想得f(n)=2(n?N*).
(2)在数列{an}中,a1=1,
由于求出 所以归纳得出2. 用归纳法写出下列数列的一个通项公式:例3.(1)已知数列{an}的通项公式:
f(n)=(1-a1)(1-a2)… (1-an),试通过计算f(1),f(2),f(3)的值,推测出f(n)的值.
(2)应用归纳推理猜测:凸四边形有2条对角线,凸五边形有5条对角线,比凸四边形多3条;凸六边形有9条对角线,比凸五边形多4条;……猜想:凸n边形的对角线条数比凸n-1边形多n-2条对角线.由此,凸n边形对角线条数为2+3+4+5+…+(n-2).凸n边形有多少条对角线?3. 凸n边形有多少条对角线?4.在同一平面内,两条直线相交,有一个交点; 三条直线相交,最多有几个交点? 四条直线相交,最多有几个交点?…… 六条直线相交,最多有几个交点?……n条直线相交,最多有几个交点?同学们.再见!例2:数一数图中的凸多面体的面数F、顶点数V和棱数E,然后用归纳法推理得出它们之间的关系.46455659846455659866861281261046455659866861281261077916910151015F+V-E=2猜想欧拉公式例3:如图有三根针和套在一根针上的若干金属片. 按下列规则,把金属片从一根针上全部移到另一根针上. 1.每次只能移动1个金属片; 2.较大的金属片不能放在较小的金属片上面.试推测;把n个金属片从1号针移到3号针,最少需要移动多少次?123当n=1时,a1=1当n=2时,a2=3解;设an表示移动n块金属片时的移动次数.当n=3时,a3=7当n=4时,a4=15猜想 an=2n -1123 歌德巴赫猜想:
“任何一个不小于6的偶数都等于两个奇质数之和”即:偶数=奇质数+奇质数 每幅地图可以用四种颜色着色,使得有共同边界的相邻区域着上不同色四色猜想 1852年,英国人弗南西斯·格思里为地图着色时,发现了四色猜想. 1976年,美国数学家阿佩尔与哈肯在两台计算机上,用了1200个小时,完成了四色猜想的证明.牛顿发现万有引力
门捷列夫发现元素周期律应用归纳推理可以
发现新事实,获得新结论!归纳推理是科学发现的重要途径!歌德巴赫猜想
四色定理猜想:费马猜想实验观察大胆猜想检验猜想归纳推理的一般步骤
—验证猜想—再提出猜想—再验证猜想的过程。案例1:蛇是用肺呼吸的,鳄鱼是用肺呼吸的,海龟是用肺呼吸的,蜥蜴是用肺呼吸的.蛇、鳄鱼、海龟、蜥蜴都是爬行动物.由此猜想:案例2:三角形的内角和是1800,凸四边形的内角和是3600,凸五边形的内角和是5400,…由此猜想:所有的爬行动物都是用肺呼吸的.凸n边形的内角和是(n-2)×1800案例3:由此猜想:推理 推理:从一个或几个已知命题得出另一个新命题的思维过程.蛇是用肺呼吸的,鳄鱼是用肺呼吸,海龟是用肺呼吸,蜥蜴是用肺呼吸。所有的爬行动物都是用肺呼吸的。三角形内角和
为
凸四边形内角
和为
凸五边形内角
和为
凸n边形内角和为部分
个别整 体
一 般 从 中推演出
的推理,通
常称为归纳推理.个别事实一般性的结论观察下列等式
3+7=10,
3+17=20,
13+17=30,归纳出一个规律:
偶数=奇质数+奇质数
通过更多特例的检验,从6开始,没有出现反例.大胆猜想: 任何一个不小于6的偶数都等于两个奇质数的和.哥德巴赫猜想
10=3+7,
20=3+17,
30=13+17.陈氏定理实验观察大胆猜想检验猜想归纳推理的一般步骤归纳推理的几个特点:1.归纳推理的前提是几个已知的特殊现象,归纳得出的结论是尚属未知的一般现象,该结论超越了前提所包容的范围.2.归纳推理得到的结论具有猜测的性质,结论是否真实,还需经过逻辑证明和实践检验.它不能作为数学证明的工具.3.归纳推理是一种具有创造性的推理.通过归纳推理得到的猜想,可以作为进一步研究的起点,帮助人们发现问题和提出问题.例1.已知数列{an}的每一项都是正数,且a1=1, ,试归纳出这个数列的一个通项公式.解.当n=1时,a1=1;当n=2时,a2=
当n=3时,a3= ;当n=4时,a4= .
……由此我们可以猜想出{an}的一个通项公式为 .1. 观察下列等式,并从中归纳出一般的结论:(1)1. 观察下列等式,并从中归纳出一般的结论:1-4+9-16+……+(-1)n+1×n2=(-1)n+1(1+2+3+……+n).例2.下面推理是归纳推理吗?所得结论正确吗?
(1)f(x)=(x-1)(x-2)…(x-100)+2,因为f(1)=2,f(2)=2,…f(100)=2,所以归纳猜想得f(n)=2(n?N*).
(2)在数列{an}中,a1=1,
由于求出 所以归纳得出2. 用归纳法写出下列数列的一个通项公式:例3.(1)已知数列{an}的通项公式:
f(n)=(1-a1)(1-a2)… (1-an),试通过计算f(1),f(2),f(3)的值,推测出f(n)的值.
(2)应用归纳推理猜测:凸四边形有2条对角线,凸五边形有5条对角线,比凸四边形多3条;凸六边形有9条对角线,比凸五边形多4条;……猜想:凸n边形的对角线条数比凸n-1边形多n-2条对角线.由此,凸n边形对角线条数为2+3+4+5+…+(n-2).凸n边形有多少条对角线?3. 凸n边形有多少条对角线?4.在同一平面内,两条直线相交,有一个交点; 三条直线相交,最多有几个交点? 四条直线相交,最多有几个交点?…… 六条直线相交,最多有几个交点?……n条直线相交,最多有几个交点?同学们.再见!例2:数一数图中的凸多面体的面数F、顶点数V和棱数E,然后用归纳法推理得出它们之间的关系.46455659846455659866861281261046455659866861281261077916910151015F+V-E=2猜想欧拉公式例3:如图有三根针和套在一根针上的若干金属片. 按下列规则,把金属片从一根针上全部移到另一根针上. 1.每次只能移动1个金属片; 2.较大的金属片不能放在较小的金属片上面.试推测;把n个金属片从1号针移到3号针,最少需要移动多少次?123当n=1时,a1=1当n=2时,a2=3解;设an表示移动n块金属片时的移动次数.当n=3时,a3=7当n=4时,a4=15猜想 an=2n -1123 歌德巴赫猜想:
“任何一个不小于6的偶数都等于两个奇质数之和”即:偶数=奇质数+奇质数 每幅地图可以用四种颜色着色,使得有共同边界的相邻区域着上不同色四色猜想 1852年,英国人弗南西斯·格思里为地图着色时,发现了四色猜想. 1976年,美国数学家阿佩尔与哈肯在两台计算机上,用了1200个小时,完成了四色猜想的证明.牛顿发现万有引力
门捷列夫发现元素周期律应用归纳推理可以
发现新事实,获得新结论!归纳推理是科学发现的重要途径!歌德巴赫猜想
四色定理猜想:费马猜想实验观察大胆猜想检验猜想归纳推理的一般步骤
