第5课时 直接证明1
图片预览








文档简介
课件27张PPT。合情推理与演绎推理的区别:①归纳推理是由特殊到一般的推理;
②类比推理是由特殊到特殊的推理;
③演绎推理是由一般到特殊的推理.
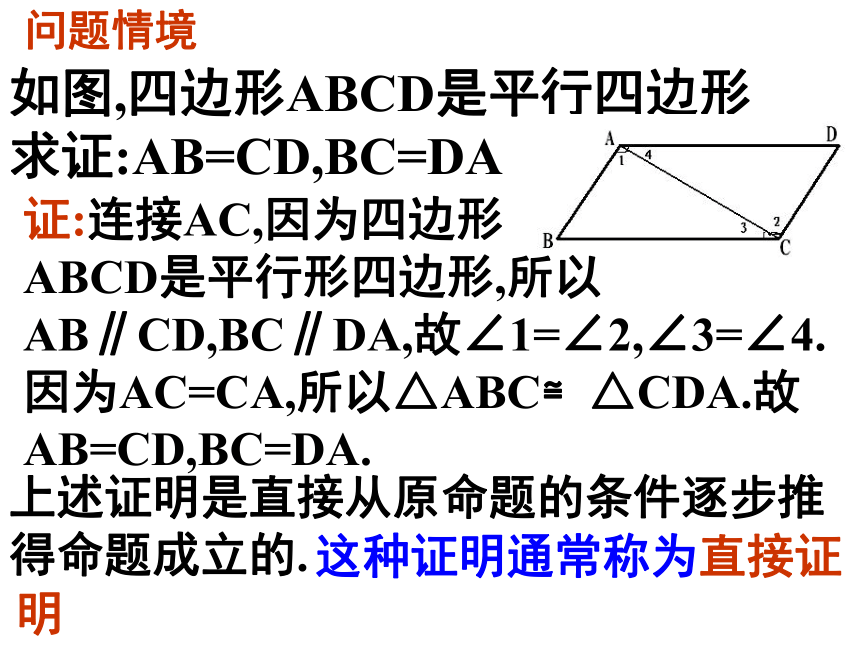
从推理的结论来看,合情推理的结论不一定正确,有待证明;演绎推理得到的结论一定正确.第90课时 直接证明(1)问题情境如图,四边形ABCD是平行四边形
求证:AB=CD,BC=DA证:连接AC,因为四边形
ABCD是平行形四边形,所以AB∥CD,BC∥DA,故∠1=∠2,∠3=∠4.因为AC=CA,所以△ABC≌△CDA.故AB=CD,BC=DA. 这种证明通常称为直接证明上述证明是直接从原命题的条件逐步推得命题成立的.直接证明1 概念:直接从原命题的条件逐步推得命题成立2 直接证明的一般形式:直接证明证法1 对于正数a,b,有直接证明证法2 要证只要证只要证只要证 因为最后一个不等式成立,故结论成立.直接证明(数学理论)上述两种证法有什么异同?都是直接证明 证法1 从已知条件出发,以已知的定义,公理,定理为依据,逐步下推,直到推出要证明的结论为止 综合法相同不同 证法2 从问题的结论出发,追溯导致结论成立的条件,逐步上溯,直到使结论成立的条件和已知条件吻合为止 分析法直接证明综合法和分析法的推证过程如下:综合法已知条件结论分析法结论 已知条件 例1.已知a,b,c是不全等的正数,求证:a(b2+c2)+b(c2+a2)+c(a2+b2)>abc直接证明(例题)直接证明证:(综合法) 因为因为所以又因为所以所以所以直接证明证: (分析法)要证明CE=DF,只需证明
为此只需证明为了证明 只需 为了证明 只需证明 也只需 因为 是对顶角,所以它们相等,从而 成立,因此命题成立. 分析法 解题方向比较明确,
利于寻找解题思路;
综合法 条理清晰,易于表述。通常以分析法寻求
思路,再用综合法有条理地
表述解题过程例3.在△ABC中,三个内角A,B,C对应的边分别为a,b,c,且A,B,C成等差数列,a,b,c成等比数列,求证: △ABC为等边三角形.例4.设x,y?R且x2-2xy+2y2=2,求证:|x+y|<10.直接证明(练习)直接证明(练习)直接证明(练习)证要证只需证明只需证明只需证明所以原命题成立.直接证明(回顾小结)分析法 解题方向比较明确,
利于寻找解题思路;
综合法 条理清晰,易于表述。通常以分析法寻求
思路,再用综合法有条理地
表述解题过程分析法
综合法概念再见!例1.已知数列{an}的每一项都是正数,且a1=1, ,试归纳出这个数列的一个通项公式.1. 观察下列等式,并从中归纳出一般的结论:(1)2. 用归纳法写出下列数列的一个通项公式:例3.(1)已知数列{an}的通项公式:
f(n)=(1-a1)(1-a2)… (1-an),试通过计算f(1),f(2),f(3)的值,推测出f(n)的值.
(2)应用归纳推理猜测:凸四边形有2条对角线,凸五边形有5条对角线,比凸四边形多3条;凸六边形有9条对角线,比凸五边形多4条;……猜想:凸n边形的对角线条数比凸n-1边形多n-2条对角线.由此,凸n边形对角线条数为2+3+4+5+…+(n-2).凸n边形有多少条对角线?3. 凸n边形有多少条对角线?4.在同一平面内,两条直线相交,有一个交点; 三条直线相交,最多有几个交点? 四条直线相交,最多有几个交点?…… 六条直线相交,最多有几个交点?……n条直线相交,最多有几个交点?同学们.再见!
②类比推理是由特殊到特殊的推理;
③演绎推理是由一般到特殊的推理.
从推理的结论来看,合情推理的结论不一定正确,有待证明;演绎推理得到的结论一定正确.第90课时 直接证明(1)问题情境如图,四边形ABCD是平行四边形
求证:AB=CD,BC=DA证:连接AC,因为四边形
ABCD是平行形四边形,所以AB∥CD,BC∥DA,故∠1=∠2,∠3=∠4.因为AC=CA,所以△ABC≌△CDA.故AB=CD,BC=DA. 这种证明通常称为直接证明上述证明是直接从原命题的条件逐步推得命题成立的.直接证明1 概念:直接从原命题的条件逐步推得命题成立2 直接证明的一般形式:直接证明证法1 对于正数a,b,有直接证明证法2 要证只要证只要证只要证 因为最后一个不等式成立,故结论成立.直接证明(数学理论)上述两种证法有什么异同?都是直接证明 证法1 从已知条件出发,以已知的定义,公理,定理为依据,逐步下推,直到推出要证明的结论为止 综合法相同不同 证法2 从问题的结论出发,追溯导致结论成立的条件,逐步上溯,直到使结论成立的条件和已知条件吻合为止 分析法直接证明综合法和分析法的推证过程如下:综合法已知条件结论分析法结论 已知条件 例1.已知a,b,c是不全等的正数,求证:a(b2+c2)+b(c2+a2)+c(a2+b2)>abc直接证明(例题)直接证明证:(综合法) 因为因为所以又因为所以所以所以直接证明证: (分析法)要证明CE=DF,只需证明
为此只需证明为了证明 只需 为了证明 只需证明 也只需 因为 是对顶角,所以它们相等,从而 成立,因此命题成立. 分析法 解题方向比较明确,
利于寻找解题思路;
综合法 条理清晰,易于表述。通常以分析法寻求
思路,再用综合法有条理地
表述解题过程例3.在△ABC中,三个内角A,B,C对应的边分别为a,b,c,且A,B,C成等差数列,a,b,c成等比数列,求证: △ABC为等边三角形.例4.设x,y?R且x2-2xy+2y2=2,求证:|x+y|<10.直接证明(练习)直接证明(练习)直接证明(练习)证要证只需证明只需证明只需证明所以原命题成立.直接证明(回顾小结)分析法 解题方向比较明确,
利于寻找解题思路;
综合法 条理清晰,易于表述。通常以分析法寻求
思路,再用综合法有条理地
表述解题过程分析法
综合法概念再见!例1.已知数列{an}的每一项都是正数,且a1=1, ,试归纳出这个数列的一个通项公式.1. 观察下列等式,并从中归纳出一般的结论:(1)2. 用归纳法写出下列数列的一个通项公式:例3.(1)已知数列{an}的通项公式:
f(n)=(1-a1)(1-a2)… (1-an),试通过计算f(1),f(2),f(3)的值,推测出f(n)的值.
(2)应用归纳推理猜测:凸四边形有2条对角线,凸五边形有5条对角线,比凸四边形多3条;凸六边形有9条对角线,比凸五边形多4条;……猜想:凸n边形的对角线条数比凸n-1边形多n-2条对角线.由此,凸n边形对角线条数为2+3+4+5+…+(n-2).凸n边形有多少条对角线?3. 凸n边形有多少条对角线?4.在同一平面内,两条直线相交,有一个交点; 三条直线相交,最多有几个交点? 四条直线相交,最多有几个交点?…… 六条直线相交,最多有几个交点?……n条直线相交,最多有几个交点?同学们.再见!
