圆的有关性质
图片预览



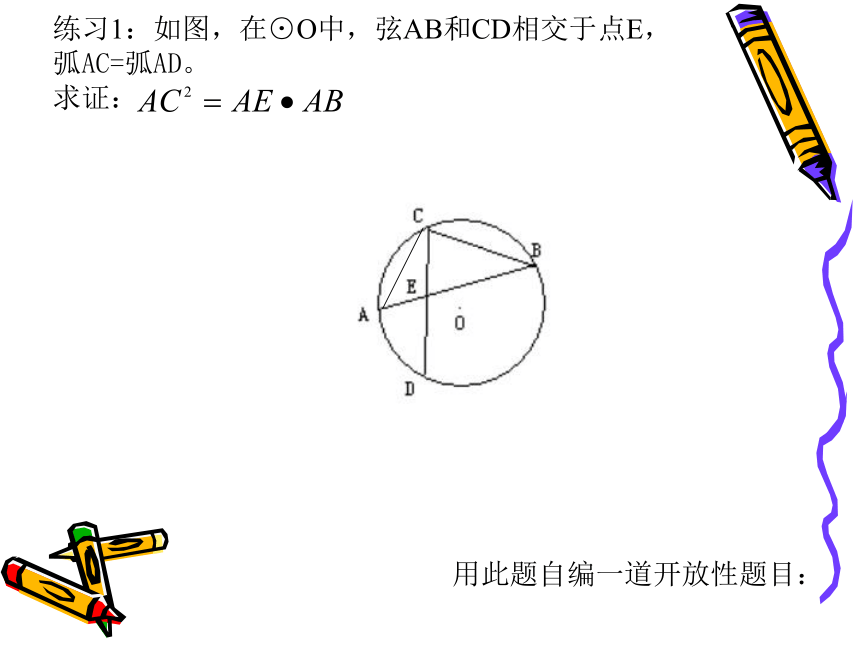
文档简介
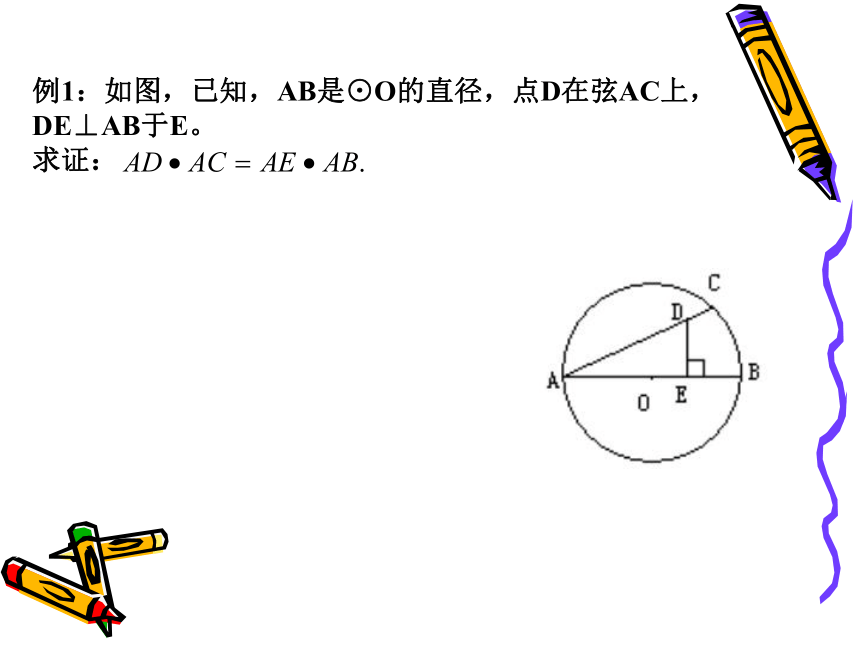
课件14张PPT。圆的有关性质的证明例1:如图,已知,AB是⊙O的直径,点D在弦AC上,
DE⊥AB于E。
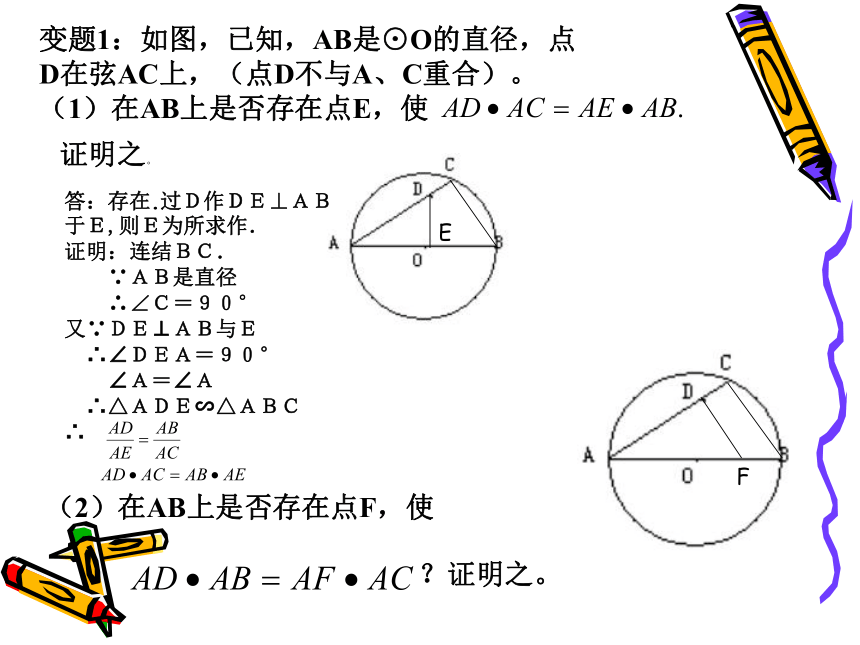
求证:变题1:如图,已知,AB是⊙O的直径,点D在弦AC上,(点D不与A、C重合)。
(1)在AB上是否存在点E,使证明之。
(2)在AB上是否存在点F,使?证明之。
EF答:存在.过D作DE⊥AB
于E,则E为所求作.
证明:连结BC.
∵AB是直径
∴∠C=90°
又∵DE⊥AB与E
∴∠DEA=90°
∠A=∠A
∴△ADE∽△ABC
∴
例2:已知: ⊙O内切于四边形ABCD,AB=AD,连接AC ,BD,如图.由这些条件,你能推出哪些结论?(要求:图中不得再标注任何字母,不得再添加辅助线.)
①AB+DC=AD+BC
②AD+BC=AB+CD
③BC=DC
④BD⊥AC
⑤∠BAC=∠DAC
⑥∠BCA=∠DCA
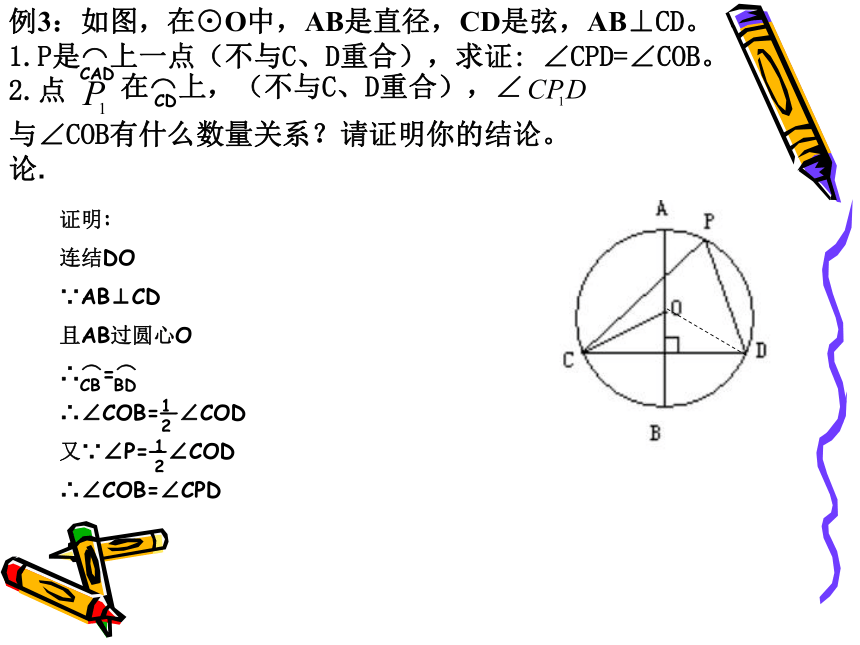
⑦∠ABC=∠ADC例3:如图,在⊙O中,AB是直径,CD是弦,AB⊥CD。
P是⌒上一点(不与C、D重合),求证: ∠CPD=∠COB。
点在⌒上,(不与C、D重合),∠与∠COB有什么数量关系?请证明你的结论。
论.CADCD证明:
连结DO
∵AB⊥CD
且AB过圆心O
∴⌒=⌒
∴∠COB=—∠COD
又∵∠P=—∠COD
∴∠COB=∠CPDCBBD1212例4:如图,BC是⊙O的直径,AD⊥BC,垂足为D,⌒=⌒,BF和AD交于点E。
试判断下列结论是否正确:(1) (2)(3) (4)2、上述(2)(3)(4)中,如果有正确的,请选择一个予以证明。
ABAF练习1:如图,在⊙O中,弦AB和CD相交于点E,
弧AC=弧AD。
求证:用此题自编一道开放性题目:已知,AE是ΔABC的外接圆的直径,AD⊥BC于点D。
求证:变题:已知,ΔABC内接于⊙O,点E在圆上,弧BE问能否在BC上找一点D,使若能,请说明确定点D的一种方法并证明;若不能,试说明理由。
>弧CE3如图, PA、PB分别切⊙O于点A、B,C是圆上异
于点A、B的任意一点,试探求∠C与∠P关系。
4练习:如图,AB为⊙O的直径,CD、CB为⊙O的切线,D、B为切点,OC交⊙O于点E,连结AE并延长交BC于F,连结AD、BD。以下结论:(1)AD∥OC;(2)点E为ΔCDB的内心;(3)FC=FE(4)其中正确的是 。
证明其中的一个正确
结论。
小结:如何解答存在性的问题:
(1)作判断
(2)把符合条件的图形(点或线)作出.
(3)证明
圆的两个重要性质的运用.
几个特征图形
图形的分解组合圆的两个重要性质的运用.CCC几个特征图形图形的分解与组合
DE⊥AB于E。
求证:变题1:如图,已知,AB是⊙O的直径,点D在弦AC上,(点D不与A、C重合)。
(1)在AB上是否存在点E,使证明之。
(2)在AB上是否存在点F,使?证明之。
EF答:存在.过D作DE⊥AB
于E,则E为所求作.
证明:连结BC.
∵AB是直径
∴∠C=90°
又∵DE⊥AB与E
∴∠DEA=90°
∠A=∠A
∴△ADE∽△ABC
∴
例2:已知: ⊙O内切于四边形ABCD,AB=AD,连接AC ,BD,如图.由这些条件,你能推出哪些结论?(要求:图中不得再标注任何字母,不得再添加辅助线.)
①AB+DC=AD+BC
②AD+BC=AB+CD
③BC=DC
④BD⊥AC
⑤∠BAC=∠DAC
⑥∠BCA=∠DCA
⑦∠ABC=∠ADC例3:如图,在⊙O中,AB是直径,CD是弦,AB⊥CD。
P是⌒上一点(不与C、D重合),求证: ∠CPD=∠COB。
点在⌒上,(不与C、D重合),∠与∠COB有什么数量关系?请证明你的结论。
论.CADCD证明:
连结DO
∵AB⊥CD
且AB过圆心O
∴⌒=⌒
∴∠COB=—∠COD
又∵∠P=—∠COD
∴∠COB=∠CPDCBBD1212例4:如图,BC是⊙O的直径,AD⊥BC,垂足为D,⌒=⌒,BF和AD交于点E。
试判断下列结论是否正确:(1) (2)(3) (4)2、上述(2)(3)(4)中,如果有正确的,请选择一个予以证明。
ABAF练习1:如图,在⊙O中,弦AB和CD相交于点E,
弧AC=弧AD。
求证:用此题自编一道开放性题目:已知,AE是ΔABC的外接圆的直径,AD⊥BC于点D。
求证:变题:已知,ΔABC内接于⊙O,点E在圆上,弧BE问能否在BC上找一点D,使若能,请说明确定点D的一种方法并证明;若不能,试说明理由。
>弧CE3如图, PA、PB分别切⊙O于点A、B,C是圆上异
于点A、B的任意一点,试探求∠C与∠P关系。
4练习:如图,AB为⊙O的直径,CD、CB为⊙O的切线,D、B为切点,OC交⊙O于点E,连结AE并延长交BC于F,连结AD、BD。以下结论:(1)AD∥OC;(2)点E为ΔCDB的内心;(3)FC=FE(4)其中正确的是 。
证明其中的一个正确
结论。
小结:如何解答存在性的问题:
(1)作判断
(2)把符合条件的图形(点或线)作出.
(3)证明
圆的两个重要性质的运用.
几个特征图形
图形的分解组合圆的两个重要性质的运用.CCC几个特征图形图形的分解与组合
