2023年广东省中考数学考前热身(一)(含解析)
文档属性
| 名称 | 2023年广东省中考数学考前热身(一)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 319.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-12 14:36:21 | ||
图片预览


文档简介
2023年广东中考数学考前热身(一)
一.选择题(共10小题,每小题3分,共30分)
1.在2,0,﹣1,﹣2这四个数中,最小的数是( )
A.﹣2 B.﹣1 C.0 D.1
2.计算﹣a2(a2)3÷(﹣a)4÷a的结果是( )
A.﹣a2 B.﹣a3 C.a4 D.﹣a4
3.如图所示的几何体是由一个圆柱体和一个长方体组成的,则这个几何体的俯视图是( )
A. B.
C. D.
4.“五一”假日期间,某省银联网络交易总金额接近2640000000元.其中2640000000用科学记数法表示为( )
A.26.4×109 B.2.64×109 C.2.64×108 D.0.264×109
5.已知点A(﹣1,﹣3)关于x轴的对称点A′在反比例函数y的图象上,则实数k的值为( )
A.﹣3 B. C. D.3
6.在某时段有50辆车通过一个雷达测速点,工作人员将测得的车速绘制成如图所示的条形统计图,则这50辆车的车速的中位数(单位:km/h)为( )
A.35 B.37.5 C.40 D.45
7.如图,△ABC中,DE∥BC,,AE=2cm,则AC的长是( )
A.2cm B.4cm
C.6cm D.8cm
8.若6﹣x>x,则下列不等式一定成立的是( )
A.x≥2 B.x<3 C.x≥4 D.x≤3
9.据国家统计局数据,2018年全年国内生产总值为90.3万亿,比2017年增长6.6%.假设国内生产总值的年增长率保持不变,则国内生产总值首次突破100万亿的年份是( )
A.2019年 B.2020年 C.2021年 D.2022年
10.如图,正方形ABCD中,AB=4,E是BC的中点,点P是对角线AC上一动点,则PE+PB的最小值为( )
A.3 B.4
C.5 D.2
二.填空题(共5小题,每小题3分,共15分)
11.分解因式:m2n﹣9n= .
12.命题“如果a+b=0,那么a,b互为相反数”的逆命题为 .
13.如图,点A,B,C是⊙O上的三点,∠B=75°,则∠AOC的大小为 度.
14.关于x的一元二次方程x2x+1=0有两个相等的实数根,则m的取值为 .
15.观察如图所示的一系列图形,它们是按一定规律排列的,依照此规律,第2021个图形中共有 个〇,第n个图形中共有 个〇.
三.解答题(一)(共3小题,每小题8分,共24分)
16.(1)解方程组:.
(2)解方程:(x﹣1)2=4.
17.(1)计算:()2﹣|2|+2cos45°﹣(3﹣π)0;
(2)先化简,再求值:,其中x1.
18.如图,已知点E,C在线段BF上,BE=CF,AB=DE,∠B=∠DEF.求证:AC∥DF.
四.解答题(二)(共3小题,每小题9分,共27分)
19.西安地铁的开通运行给市民的出行方式带来了一些变化,乐乐和小敏在五一放假期间以问卷的方式对西安市民对地铁的满意度进行调查,如图是西安地铁四号线图(部分),乐乐和小敏分别从飞天路(用A表示)、东长安街(用B表示)、神州大道(用C表示)三站中,随机选取一站作为调查的站点.
(1)在这三站中,乐乐选取的站点为飞天路的概率为 ;
(2)请你用画树状图或列表的方法,求乐乐和小敏所选取问卷调查的站点相邻的概率.
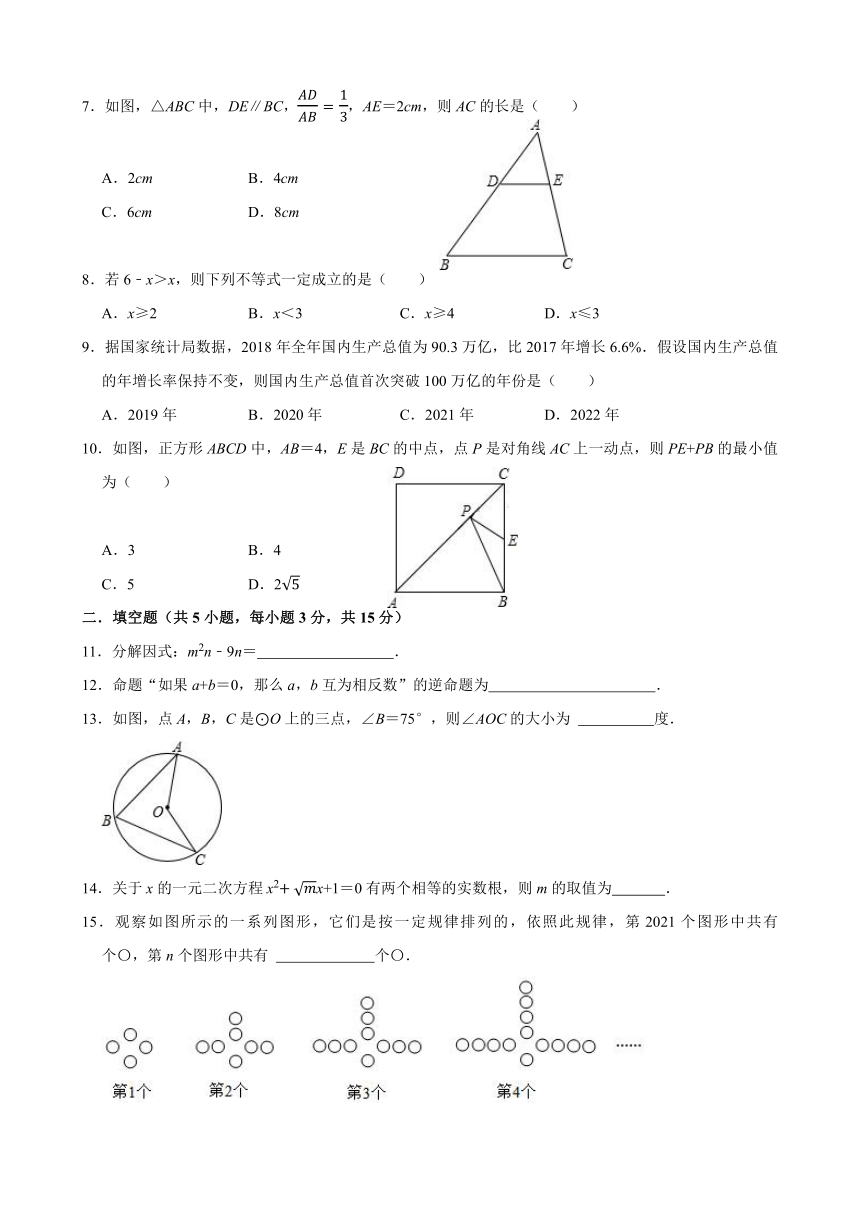
20.台灯是生活中常见物品,图①是一个台灯的实物图,图②是其侧面示意图.台灯的双轴灯臂,AB=9cm,AC=37cm,通过调节灯臂AC的倾斜角度∠CAC'可以改变台灯的照明位置,已知AB垂直于底座,∠CAC'=23°,求灯臂顶端C到底座的距离CE的长度(结果精确到1cm).(参考数据:sin23°=0.39,cos23°=0.92,tan23°=0.42)
21.某学校为了给学生提供更舒适的学习环境,决定购进A,B两种空调.已知购买1台A种空调和3台B种空调共需9300元;购买3台A种空调和2台B种空调共需13200元.
(1)求A,B两种空调的单价;
(2)若该校准备购买A,B两种空调共50台,且A种空调数量不小于B种空调数量的2倍,请你设计出最省钱的购买方案,并说明理由.
五.解答题(三)(共3小题,每小题12分,共24分)
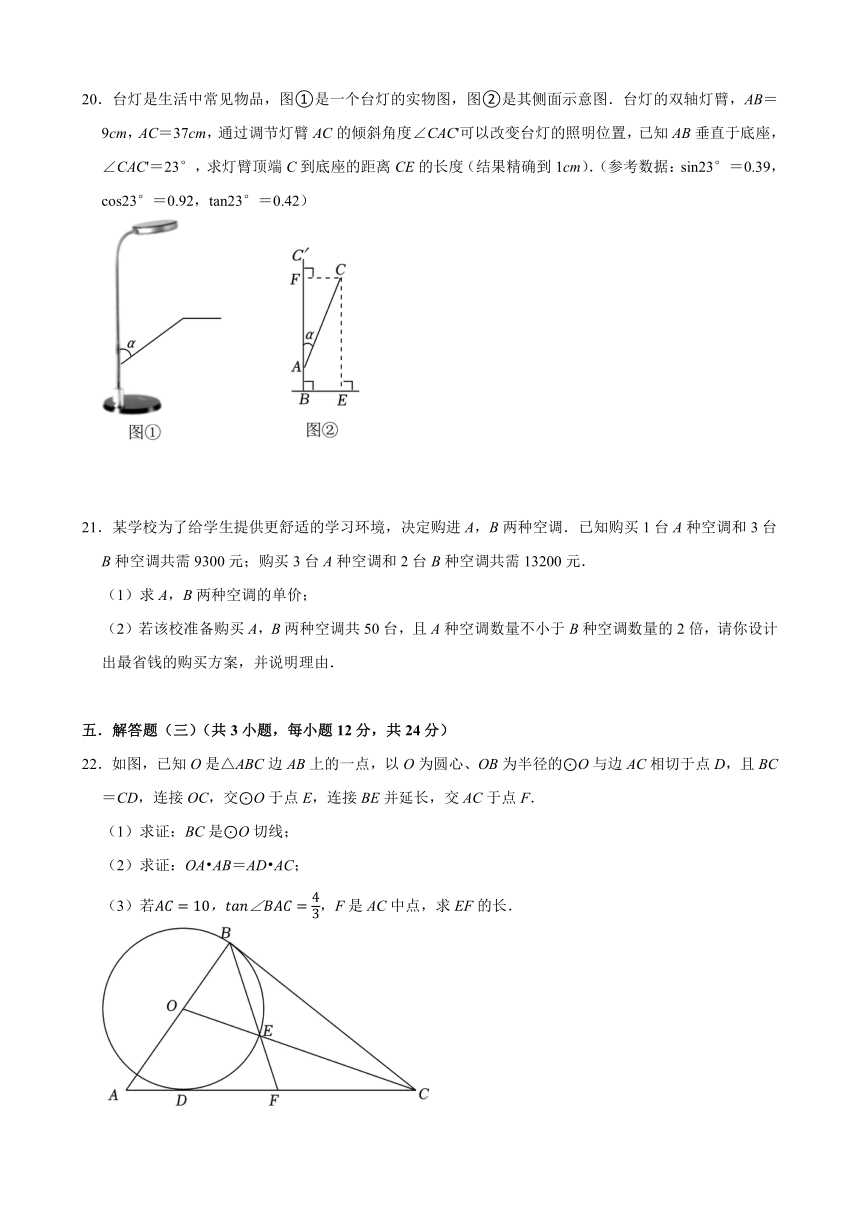
22.如图,已知O是△ABC边AB上的一点,以O为圆心、OB为半径的⊙O与边AC相切于点D,且BC=CD,连接OC,交⊙O于点E,连接BE并延长,交AC于点F.
(1)求证:BC是⊙O切线;
(2)求证:OA AB=AD AC;
(3)若,F是AC中点,求EF的长.
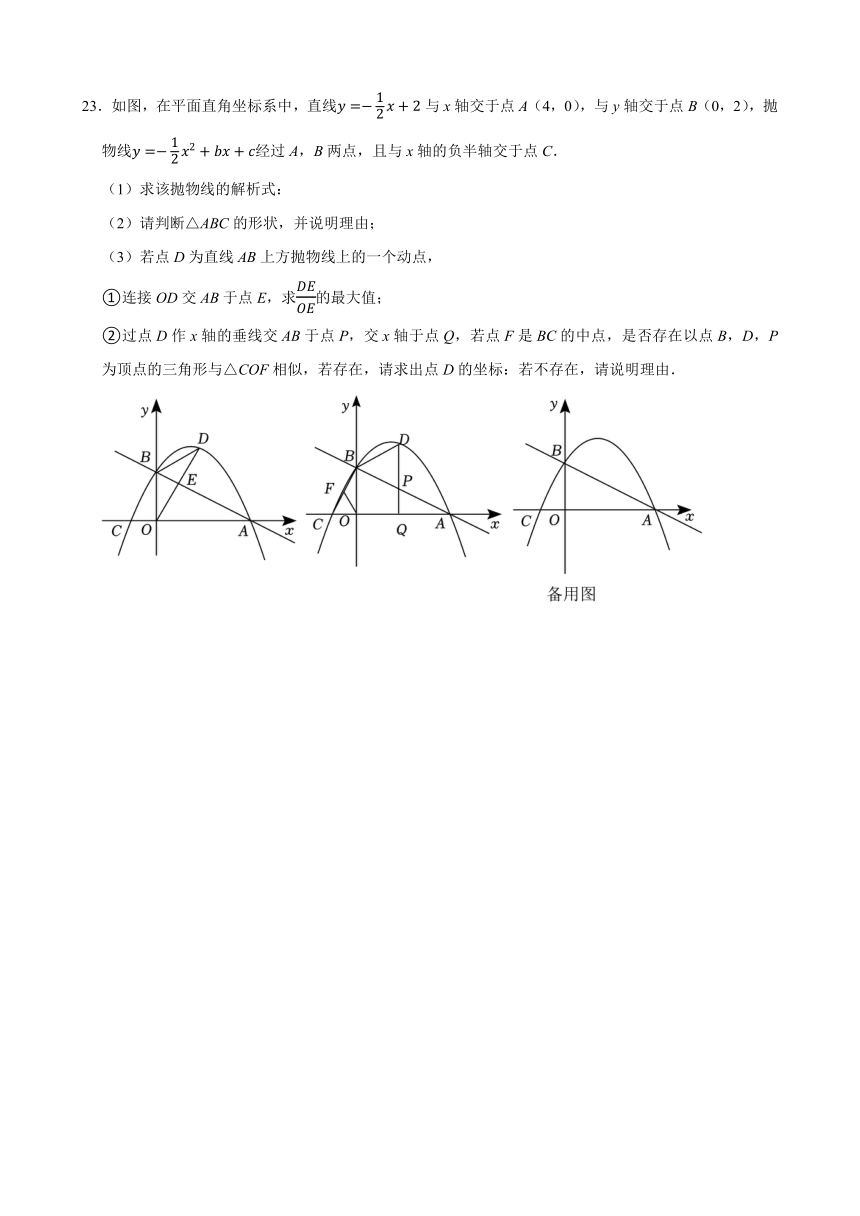
23.如图,在平面直角坐标系中,直线与x轴交于点A(4,0),与y轴交于点B(0,2),抛物线经过A,B两点,且与x轴的负半轴交于点C.
(1)求该抛物线的解析式:
(2)请判断△ABC的形状,并说明理由;
(3)若点D为直线AB上方抛物线上的一个动点,
①连接OD交AB于点E,求的最大值;
②过点D作x轴的垂线交AB于点P,交x轴于点Q,若点F是BC的中点,是否存在以点B,D,P为顶点的三角形与△COF相似,若存在,请求出点D的坐标:若不存在,请说明理由.
2023年广东中考数学考前热身(一)
参考答案与试题解析
一.选择题(共10小题)
1.【解答】解:根据有理数比较大小的方法,可得
﹣2<﹣1<0<2,
故在2,0,﹣1,﹣2这四个数中,最小的数是﹣2.
故选:A.
2.【解答】解:原式=﹣a2 a6÷a4÷a=﹣a8÷a4÷a=﹣a3.
故选:B.
3.【解答】解:从上面看外边是一个矩形,里面是一个圆,
故选:C.
4.【解答】解:2640000000=2.64×109.
故选:B.
5.【解答】解:点A(﹣1,﹣3)关于x轴的对称点A'的坐标为(﹣1,3),
把A′(﹣1,3)代入y得k=﹣1×3=﹣3.
故选:A.
6.【解答】解:∵50辆车的车速的中位数是位于第25位和第26位两个数的平均数,
由条形图知,车第25位和第26位两个数是40和40,
∴这50辆车的车速的中位数为40km/h;
故选:C.
7.【解答】解:∵DE∥BC,
∴,
∵,AE=2cm,
∴,
∴AC=6(cm),
故选:C.
8.【解答】解:解不等式6﹣x>x,
移项,合并同类项,得﹣2x>﹣6,
不等式两边都除以﹣2,得:x<3,
故选:B.
9.【解答】解:2019年全年国内生产总值为:90.3×(1+6.6%)=96.2598(万亿),
2020年全年国内生产总值为:96.2598×(1+6.6%)≈102.6(万亿),
∴国内生产总值首次突破100万亿的年份是2020年,
故选:B.
10.【解答】解:连接DE,交AC于点P,连接BD.
∵点B与点D关于AC对称,
∴DE的长即为PE+PB的最小值,
∵AB=4,E是BC的中点,
∴CE=2,
在Rt△CDE中,
DE2.
故选:D.
二.填空题(共5小题)
11.【解答】解:m2n﹣9n
=n(m2﹣9)
=n(m+3)(m﹣3),
故答案为:n(m+3)(m﹣3).
12.【解答】解:命题“如果a+b=0,那么a,b互为相反数”的逆命题为:
如果a,b互为相反数,那么a+b=0;
故答案为:如果a,b互为相反数,那么a+b=0.
13.【解答】解:∵,
∴∠AOC=2∠B=150°,
故答案为150.
14.【解答】解:
由题意,Δ=b2﹣4ac=()2﹣4=0
得m=4
故答案为4
15.【解答】解:观察图形的变化可知:
第1个图形中共有3×1+1=4个〇;
第2个图形中共有3×2+1=7个〇;
第3个图形中共有3×3+1=10个〇;
…
所以第n个图形中共有(3n+1)个〇;
所以第2021个图形中共有〇的个数为:3×2021+1=6064.
故答案为:6064,(3n+1).
三.解答题(共8小题)
16.【解答】解:(1)
①×3,得6x﹣3y=12,③
②+③得10x=10,
∴x=1,
把x=1代入①得2﹣y=4,
∴y=﹣2,
∴方程组的解为:.
(2)∵(x﹣1)2=4,
∴x﹣1=±2,
∴x﹣1=2或x﹣1=﹣2,
∴x=3或﹣1.
17.【解答】解:(1)原式221
21
2;
(2)原式[]
,
当x1时,原式.
18.【解答】证明:∵BE=CF,
∴BE+EC=CF+EC,
即BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS),
∴∠ACB=∠DFE,
∴AC∥DF.
19.【解答】解:(1)在这三站中,乐乐选取的站点为飞天路的概率为,
故答案为:;
(2)列表如下:
A B C
A (A,A) (B,A) (C,A)
B (A,B) (B,B) (C,B)
C (A,C) (B,C) (C,C)
由表知,共有9种等可能结果,其中乐乐和小敏所选取问卷调查的站点相邻的有4种结果,
所以乐乐和小敏所选取问卷调查的站点相邻的概率为.
20.【解答】解:过点C作CE⊥BE于点E,过点C作CF⊥AB于点F,
∵AB垂直于底座,
∴四边形FBEC是矩形,
∴CE=FB,
在 Rt△ACF 中,
∵AC=37,∠CAF=23°,
,
∴AF=AC cos∠CAF=37×cos23°=≈37×0.92=34.04(cm),
∴CE=BF=AB+AF=9+37.04≈46(cm).
答:灯臂顶端C到底座的距离CE的长度约为46cm.
21.【解答】解:(1)设A种空调的单价是x元,B种空调的单价是y元,
依题意得:,
解得:.
答:A种空调的单价是3000元,B种空调的单价是2100元.
(2)设购进A型空调m台,则购进B型空调(50﹣m)台,购买所需费用为w元.
依题意得:w=3000m+2100(50﹣m),
化简整理得:w=900m+105000,
由题意得:m≥2(50﹣m),
解得:m≥33,
∵900>0,
∴w随m的增大而增大,
∴当m=33时,w有最小值,此时最小值为900×33+105000=134700(元).
答:最省钱的购买方案是:购进A型空调33台,购进B型空调17台.
22.【解答】(1)证明:如图,连接OD,
∵AC与圆O相切于点D,
∴OD⊥AC,即∠ODC=90°,
∵BC=CD,BC=DC,CO=CO,
∴△OBC≌△ODC(SSS),
∴∠OBC=∠ODC=90°,即OB⊥CB,
∴BC是圆O的切线;
(2)证明:∵OD⊥AC,
∴∠ADO=90°.
∵∠OBC=90°,
∴∠ADO=∠ABC.
又∵∠BAC=∠DAO,
∴△AOD∽△ACB,
∴,
∴AO AB=AC AD;
(3)解:∵∠OBC=90°,
∴,
设AB=3x,则BC=4x.
∵AB2+BC2=AC2,
∴(3x)2+(4x)2=102,
解得:x=2(舍去负值),
∴AB=6,BC=8.
∵OD⊥AC,
∴,
设OD=4y,
则OB=4y,AD=3y,
∴,
∴AB=OA+OB=9y=6,
解得:,
∴,即⊙O半径为.
∵F是AC中点,
∴,
∴∠ABF=∠BAF.
∵OB=OE,
∴∠OBE=∠OEB,
∴∠ABF=∠BAF=∠OBE=∠OEB,
∴△OBE∽△FBA,
∴,即,
解得:,
∴.
23.【解答】解:(1)∵抛物线经过A(4,0),B(0,2),
∴,
解得:,
∴;
(2)△ABC是直角三角形,理由如下:
令y=0得,,
解得:x1=4,x2=﹣1,
∴C(﹣1,0),
∴OC=1,
∵A(4,0),B(0,2),
∴OA=4,OB=2,
∴AC=OC+OA=5,
在Rt△BOC中,BC,
在Rt△AOB中,AB,
∵BC2=5,AB2=20,AC2=25,
∴BC2+AB2=AC2,
∴△ABC是直角三角形;
(3)①如图,过点D作DF⊥AC于点F,交AB于点G,
∵BO⊥AC,DF⊥AC,
∴BO∥DF,
∴△DEG∽△OEB,
∴,
∵OB=2,
∴当DG取的最大值时,取得最大值,
设D,则G,
∴DG=yD﹣yG,
∵,
∴当a=2时,DG取的最大值2,
此时,即的最大值为1;
②在Rt△BOC中,点F是BC的中点,
∴OF=BF=CF,
∴△COF为等腰三角形,
由(1)可知,∠ABC=90°,
∴∠CBO+∠ABO=90°,
∵∠CBO+∠OCF=90°,
∴∠ABO=∠OCF,
∵DQ⊥x轴,BO⊥x轴,
∴DQ∥BO,
∴∠BPD=∠ABO=∠OCF,
要使以点B,D,P为顶点的三角形与△COF相似,
则△BPD为等腰三角形,且∠BPD为底角,
∴BD=DP或BP=BD,
当BD=DP时,即∠BPD=∠DBP,
设D,则P,
∴DP,
BD,
由BD=DP可得BD2=DP2,
∴,
解得:m1=m2=0(舍去),m3,
∴D;
当BP=BD时,即∠BPD=∠BDP,
如图,过点B作BM⊥DP于点M,
则yB=yM=2,且M为DP的中点,
设D,则P,
∴yM2,
解得:m1=0(舍去),m2=2,
∴D(2,3).
综上,点D的坐标为或(2,3).
一.选择题(共10小题,每小题3分,共30分)
1.在2,0,﹣1,﹣2这四个数中,最小的数是( )
A.﹣2 B.﹣1 C.0 D.1
2.计算﹣a2(a2)3÷(﹣a)4÷a的结果是( )
A.﹣a2 B.﹣a3 C.a4 D.﹣a4
3.如图所示的几何体是由一个圆柱体和一个长方体组成的,则这个几何体的俯视图是( )
A. B.
C. D.
4.“五一”假日期间,某省银联网络交易总金额接近2640000000元.其中2640000000用科学记数法表示为( )
A.26.4×109 B.2.64×109 C.2.64×108 D.0.264×109
5.已知点A(﹣1,﹣3)关于x轴的对称点A′在反比例函数y的图象上,则实数k的值为( )
A.﹣3 B. C. D.3
6.在某时段有50辆车通过一个雷达测速点,工作人员将测得的车速绘制成如图所示的条形统计图,则这50辆车的车速的中位数(单位:km/h)为( )
A.35 B.37.5 C.40 D.45
7.如图,△ABC中,DE∥BC,,AE=2cm,则AC的长是( )
A.2cm B.4cm
C.6cm D.8cm
8.若6﹣x>x,则下列不等式一定成立的是( )
A.x≥2 B.x<3 C.x≥4 D.x≤3
9.据国家统计局数据,2018年全年国内生产总值为90.3万亿,比2017年增长6.6%.假设国内生产总值的年增长率保持不变,则国内生产总值首次突破100万亿的年份是( )
A.2019年 B.2020年 C.2021年 D.2022年
10.如图,正方形ABCD中,AB=4,E是BC的中点,点P是对角线AC上一动点,则PE+PB的最小值为( )
A.3 B.4
C.5 D.2
二.填空题(共5小题,每小题3分,共15分)
11.分解因式:m2n﹣9n= .
12.命题“如果a+b=0,那么a,b互为相反数”的逆命题为 .
13.如图,点A,B,C是⊙O上的三点,∠B=75°,则∠AOC的大小为 度.
14.关于x的一元二次方程x2x+1=0有两个相等的实数根,则m的取值为 .
15.观察如图所示的一系列图形,它们是按一定规律排列的,依照此规律,第2021个图形中共有 个〇,第n个图形中共有 个〇.
三.解答题(一)(共3小题,每小题8分,共24分)
16.(1)解方程组:.
(2)解方程:(x﹣1)2=4.
17.(1)计算:()2﹣|2|+2cos45°﹣(3﹣π)0;
(2)先化简,再求值:,其中x1.
18.如图,已知点E,C在线段BF上,BE=CF,AB=DE,∠B=∠DEF.求证:AC∥DF.
四.解答题(二)(共3小题,每小题9分,共27分)
19.西安地铁的开通运行给市民的出行方式带来了一些变化,乐乐和小敏在五一放假期间以问卷的方式对西安市民对地铁的满意度进行调查,如图是西安地铁四号线图(部分),乐乐和小敏分别从飞天路(用A表示)、东长安街(用B表示)、神州大道(用C表示)三站中,随机选取一站作为调查的站点.
(1)在这三站中,乐乐选取的站点为飞天路的概率为 ;
(2)请你用画树状图或列表的方法,求乐乐和小敏所选取问卷调查的站点相邻的概率.
20.台灯是生活中常见物品,图①是一个台灯的实物图,图②是其侧面示意图.台灯的双轴灯臂,AB=9cm,AC=37cm,通过调节灯臂AC的倾斜角度∠CAC'可以改变台灯的照明位置,已知AB垂直于底座,∠CAC'=23°,求灯臂顶端C到底座的距离CE的长度(结果精确到1cm).(参考数据:sin23°=0.39,cos23°=0.92,tan23°=0.42)
21.某学校为了给学生提供更舒适的学习环境,决定购进A,B两种空调.已知购买1台A种空调和3台B种空调共需9300元;购买3台A种空调和2台B种空调共需13200元.
(1)求A,B两种空调的单价;
(2)若该校准备购买A,B两种空调共50台,且A种空调数量不小于B种空调数量的2倍,请你设计出最省钱的购买方案,并说明理由.
五.解答题(三)(共3小题,每小题12分,共24分)
22.如图,已知O是△ABC边AB上的一点,以O为圆心、OB为半径的⊙O与边AC相切于点D,且BC=CD,连接OC,交⊙O于点E,连接BE并延长,交AC于点F.
(1)求证:BC是⊙O切线;
(2)求证:OA AB=AD AC;
(3)若,F是AC中点,求EF的长.
23.如图,在平面直角坐标系中,直线与x轴交于点A(4,0),与y轴交于点B(0,2),抛物线经过A,B两点,且与x轴的负半轴交于点C.
(1)求该抛物线的解析式:
(2)请判断△ABC的形状,并说明理由;
(3)若点D为直线AB上方抛物线上的一个动点,
①连接OD交AB于点E,求的最大值;
②过点D作x轴的垂线交AB于点P,交x轴于点Q,若点F是BC的中点,是否存在以点B,D,P为顶点的三角形与△COF相似,若存在,请求出点D的坐标:若不存在,请说明理由.
2023年广东中考数学考前热身(一)
参考答案与试题解析
一.选择题(共10小题)
1.【解答】解:根据有理数比较大小的方法,可得
﹣2<﹣1<0<2,
故在2,0,﹣1,﹣2这四个数中,最小的数是﹣2.
故选:A.
2.【解答】解:原式=﹣a2 a6÷a4÷a=﹣a8÷a4÷a=﹣a3.
故选:B.
3.【解答】解:从上面看外边是一个矩形,里面是一个圆,
故选:C.
4.【解答】解:2640000000=2.64×109.
故选:B.
5.【解答】解:点A(﹣1,﹣3)关于x轴的对称点A'的坐标为(﹣1,3),
把A′(﹣1,3)代入y得k=﹣1×3=﹣3.
故选:A.
6.【解答】解:∵50辆车的车速的中位数是位于第25位和第26位两个数的平均数,
由条形图知,车第25位和第26位两个数是40和40,
∴这50辆车的车速的中位数为40km/h;
故选:C.
7.【解答】解:∵DE∥BC,
∴,
∵,AE=2cm,
∴,
∴AC=6(cm),
故选:C.
8.【解答】解:解不等式6﹣x>x,
移项,合并同类项,得﹣2x>﹣6,
不等式两边都除以﹣2,得:x<3,
故选:B.
9.【解答】解:2019年全年国内生产总值为:90.3×(1+6.6%)=96.2598(万亿),
2020年全年国内生产总值为:96.2598×(1+6.6%)≈102.6(万亿),
∴国内生产总值首次突破100万亿的年份是2020年,
故选:B.
10.【解答】解:连接DE,交AC于点P,连接BD.
∵点B与点D关于AC对称,
∴DE的长即为PE+PB的最小值,
∵AB=4,E是BC的中点,
∴CE=2,
在Rt△CDE中,
DE2.
故选:D.
二.填空题(共5小题)
11.【解答】解:m2n﹣9n
=n(m2﹣9)
=n(m+3)(m﹣3),
故答案为:n(m+3)(m﹣3).
12.【解答】解:命题“如果a+b=0,那么a,b互为相反数”的逆命题为:
如果a,b互为相反数,那么a+b=0;
故答案为:如果a,b互为相反数,那么a+b=0.
13.【解答】解:∵,
∴∠AOC=2∠B=150°,
故答案为150.
14.【解答】解:
由题意,Δ=b2﹣4ac=()2﹣4=0
得m=4
故答案为4
15.【解答】解:观察图形的变化可知:
第1个图形中共有3×1+1=4个〇;
第2个图形中共有3×2+1=7个〇;
第3个图形中共有3×3+1=10个〇;
…
所以第n个图形中共有(3n+1)个〇;
所以第2021个图形中共有〇的个数为:3×2021+1=6064.
故答案为:6064,(3n+1).
三.解答题(共8小题)
16.【解答】解:(1)
①×3,得6x﹣3y=12,③
②+③得10x=10,
∴x=1,
把x=1代入①得2﹣y=4,
∴y=﹣2,
∴方程组的解为:.
(2)∵(x﹣1)2=4,
∴x﹣1=±2,
∴x﹣1=2或x﹣1=﹣2,
∴x=3或﹣1.
17.【解答】解:(1)原式221
21
2;
(2)原式[]
,
当x1时,原式.
18.【解答】证明:∵BE=CF,
∴BE+EC=CF+EC,
即BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS),
∴∠ACB=∠DFE,
∴AC∥DF.
19.【解答】解:(1)在这三站中,乐乐选取的站点为飞天路的概率为,
故答案为:;
(2)列表如下:
A B C
A (A,A) (B,A) (C,A)
B (A,B) (B,B) (C,B)
C (A,C) (B,C) (C,C)
由表知,共有9种等可能结果,其中乐乐和小敏所选取问卷调查的站点相邻的有4种结果,
所以乐乐和小敏所选取问卷调查的站点相邻的概率为.
20.【解答】解:过点C作CE⊥BE于点E,过点C作CF⊥AB于点F,
∵AB垂直于底座,
∴四边形FBEC是矩形,
∴CE=FB,
在 Rt△ACF 中,
∵AC=37,∠CAF=23°,
,
∴AF=AC cos∠CAF=37×cos23°=≈37×0.92=34.04(cm),
∴CE=BF=AB+AF=9+37.04≈46(cm).
答:灯臂顶端C到底座的距离CE的长度约为46cm.
21.【解答】解:(1)设A种空调的单价是x元,B种空调的单价是y元,
依题意得:,
解得:.
答:A种空调的单价是3000元,B种空调的单价是2100元.
(2)设购进A型空调m台,则购进B型空调(50﹣m)台,购买所需费用为w元.
依题意得:w=3000m+2100(50﹣m),
化简整理得:w=900m+105000,
由题意得:m≥2(50﹣m),
解得:m≥33,
∵900>0,
∴w随m的增大而增大,
∴当m=33时,w有最小值,此时最小值为900×33+105000=134700(元).
答:最省钱的购买方案是:购进A型空调33台,购进B型空调17台.
22.【解答】(1)证明:如图,连接OD,
∵AC与圆O相切于点D,
∴OD⊥AC,即∠ODC=90°,
∵BC=CD,BC=DC,CO=CO,
∴△OBC≌△ODC(SSS),
∴∠OBC=∠ODC=90°,即OB⊥CB,
∴BC是圆O的切线;
(2)证明:∵OD⊥AC,
∴∠ADO=90°.
∵∠OBC=90°,
∴∠ADO=∠ABC.
又∵∠BAC=∠DAO,
∴△AOD∽△ACB,
∴,
∴AO AB=AC AD;
(3)解:∵∠OBC=90°,
∴,
设AB=3x,则BC=4x.
∵AB2+BC2=AC2,
∴(3x)2+(4x)2=102,
解得:x=2(舍去负值),
∴AB=6,BC=8.
∵OD⊥AC,
∴,
设OD=4y,
则OB=4y,AD=3y,
∴,
∴AB=OA+OB=9y=6,
解得:,
∴,即⊙O半径为.
∵F是AC中点,
∴,
∴∠ABF=∠BAF.
∵OB=OE,
∴∠OBE=∠OEB,
∴∠ABF=∠BAF=∠OBE=∠OEB,
∴△OBE∽△FBA,
∴,即,
解得:,
∴.
23.【解答】解:(1)∵抛物线经过A(4,0),B(0,2),
∴,
解得:,
∴;
(2)△ABC是直角三角形,理由如下:
令y=0得,,
解得:x1=4,x2=﹣1,
∴C(﹣1,0),
∴OC=1,
∵A(4,0),B(0,2),
∴OA=4,OB=2,
∴AC=OC+OA=5,
在Rt△BOC中,BC,
在Rt△AOB中,AB,
∵BC2=5,AB2=20,AC2=25,
∴BC2+AB2=AC2,
∴△ABC是直角三角形;
(3)①如图,过点D作DF⊥AC于点F,交AB于点G,
∵BO⊥AC,DF⊥AC,
∴BO∥DF,
∴△DEG∽△OEB,
∴,
∵OB=2,
∴当DG取的最大值时,取得最大值,
设D,则G,
∴DG=yD﹣yG,
∵,
∴当a=2时,DG取的最大值2,
此时,即的最大值为1;
②在Rt△BOC中,点F是BC的中点,
∴OF=BF=CF,
∴△COF为等腰三角形,
由(1)可知,∠ABC=90°,
∴∠CBO+∠ABO=90°,
∵∠CBO+∠OCF=90°,
∴∠ABO=∠OCF,
∵DQ⊥x轴,BO⊥x轴,
∴DQ∥BO,
∴∠BPD=∠ABO=∠OCF,
要使以点B,D,P为顶点的三角形与△COF相似,
则△BPD为等腰三角形,且∠BPD为底角,
∴BD=DP或BP=BD,
当BD=DP时,即∠BPD=∠DBP,
设D,则P,
∴DP,
BD,
由BD=DP可得BD2=DP2,
∴,
解得:m1=m2=0(舍去),m3,
∴D;
当BP=BD时,即∠BPD=∠BDP,
如图,过点B作BM⊥DP于点M,
则yB=yM=2,且M为DP的中点,
设D,则P,
∴yM2,
解得:m1=0(舍去),m2=2,
∴D(2,3).
综上,点D的坐标为或(2,3).
同课章节目录
