正方形性质[下学期]
图片预览



文档简介
课件15张PPT。正方形汉川市实验中学八年级数学组制作:飞沙落日观察与实验一:1.回顾一下,矩形与菱形是怎样由平行四边形变化得到的?
2.怎么把矩形、菱形、平行四边形变成正方形呢?几何画板演示怎样给正方形下定义呢平行四边形矩形菱形正方形有一个角是直角有一个角是直角一组邻边相等一组邻边相等有一个角是直角
且有一组邻边相等正方形的定义: 有一组邻边相等并且有一个角是直角
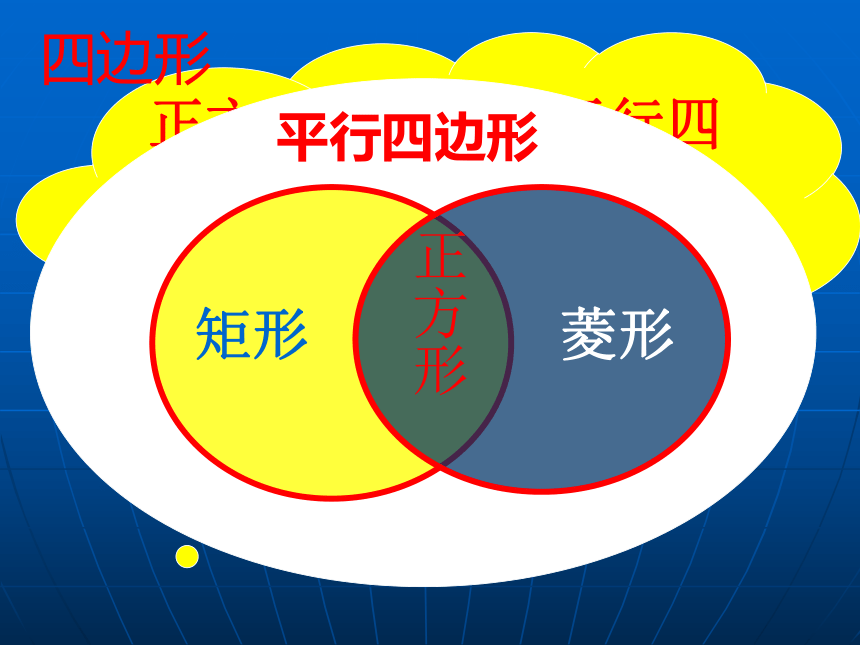
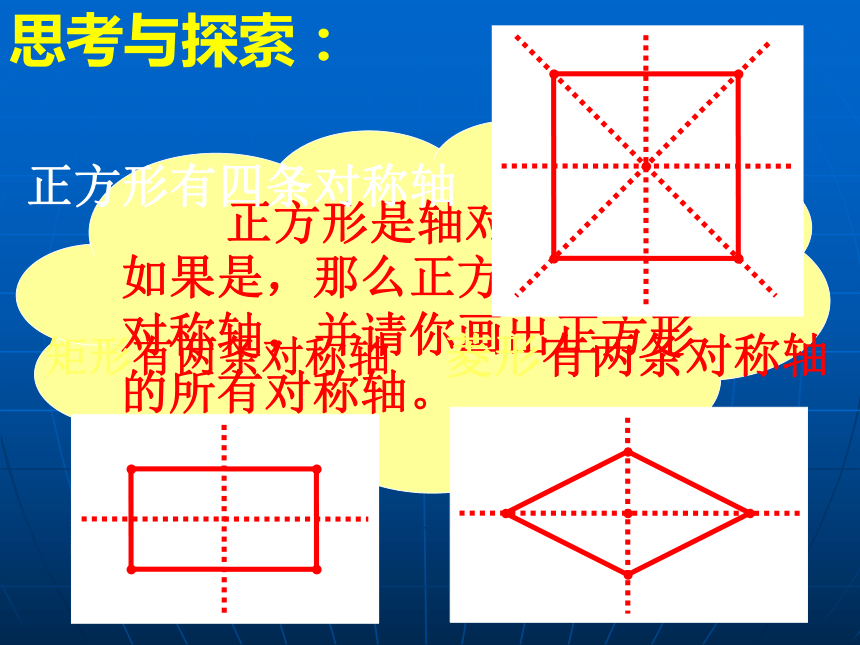
的平行四边形叫做正方形 正方形既是有一组邻边相等的矩形,又是有一个角是直角的菱形正方形是特殊的平行四边形、矩形、菱形,那么正方形与它们之间的有怎样的关系呢四边形平行四边形矩形菱形正方形思考与探索: 正方形是特殊的平行四边形、矩形、菱形,那么正方形会具有那些性质呢?边对角线对边平行四边相等对角线相等 互相垂直平分每条对角线平分一组对角四个角相等且都是直角角正方形性质 如图,四边形ABCD是正方形,请你用符号语言写出正方形ABCD的性质。思考与探索: 正方形是轴对称图形吗?如果是,那么正方形有几条对称轴,并请你画出正方形的所有对称轴。矩形有两条对称轴菱形有两条对称轴正方形有四条对称轴试一试,相信你很棒!1.正方形具有而菱形不一定具有的性质是( )
A.对角线互相垂直 B.对角线互相平分
C.对角线相等 D.对角线平分一组对角C2.从四边形内能找一点,使该点到各边距离都相等的
图形可能是 ( )
A.平行四边形、矩形、菱形 B.菱形、矩形 、正方形
C.矩形、正方形 D.菱形、正方形D3.已知正方形的一条边长为2cm,则这个正方形的
周长为 ,对角线长为 ,面积为 .8cm 4.正方形的对角线和它的边所成的角是 度.45°5.已知正方形的一条对角线长为4cm,则它的边长
为 , 面积为 。6.已知正方形ABCD中,对角线AC=10cm,P为AB上任意一
点,PE⊥AC,PF⊥BD,E、F为垂足,则PE+PF= 。5cm范例分析:例1 求证:正方形的两条对角线把正方形分成四个全等的等腰直角三角形。已知:四边形ABCD是正方形,对角线AC、BD相交于O。求证:⊿ABO、⊿BCO、⊿CDO、⊿DAO是全等的等腰直角三角形证明:∵ 四边形ABCD是正方形,∴ AC=BD,AC⊥BD,AO=CO=BO=DO﹙正方形的两条对角线相等,并且互相垂直平分﹚∴⊿ABO、⊿BCO、⊿CDO、⊿DAO都是等腰直角三角形,并且⊿ABO≌⊿BCO≌⊿CDO≌⊿DAO。拓展讨论图中有多少个等腰直角三角形? ⊿ABO、⊿BCO、⊿CDO、⊿DAO、
⊿ABC、 ⊿BCD、 ⊿CDA、 ⊿DAB。练习:P112 1、2、3、归纳与小结 回顾一下,这节课我们学习了哪些内容?1、正方形的定义: 有一组邻边相等并且有一个角是直角
的平行四边形叫做正方形 正方形既是有一组邻边相等的矩形,又是有一个角是直角的菱形 2、平行四边形、矩形、菱形和正方形的关系。3正方形的性质4、正方形的周长、面积的求法。周长:C=4a设边长为a,对角线长为m作业课本第113---114 7 8 13 1.已知:如图,正方形ABCD中,E为CD边上一点,F为BC延长线上一点,CE=CF。﹙1﹚求证:⊿BCE≌⊿DCF;﹙2﹚若∠BEC=60°,求∠EFD的度数。活动与探索ABCDEF活动与探索 2.如图正方形ABCD的边长为2,E为BC的中点,P为对角线BD上的一动点。那么当P在什么位置时,CP+EP最小,最小值是多少?注:由正方形的轴对称性知道:AP=CP活动与探索ABCDEF 3.已知:如图,AC为正方形ABCD的对角线,E为AC上一点,且AB=AE,EF⊥AC交BC于F.求证:EC=EF=FB.活动与探索 4.如图正方形ABCD的边长为1,E、F分别为BC、CD上的点,且⊿CEF的周长为2,求∠EAF的度数
2.怎么把矩形、菱形、平行四边形变成正方形呢?几何画板演示怎样给正方形下定义呢平行四边形矩形菱形正方形有一个角是直角有一个角是直角一组邻边相等一组邻边相等有一个角是直角
且有一组邻边相等正方形的定义: 有一组邻边相等并且有一个角是直角
的平行四边形叫做正方形 正方形既是有一组邻边相等的矩形,又是有一个角是直角的菱形正方形是特殊的平行四边形、矩形、菱形,那么正方形与它们之间的有怎样的关系呢四边形平行四边形矩形菱形正方形思考与探索: 正方形是特殊的平行四边形、矩形、菱形,那么正方形会具有那些性质呢?边对角线对边平行四边相等对角线相等 互相垂直平分每条对角线平分一组对角四个角相等且都是直角角正方形性质 如图,四边形ABCD是正方形,请你用符号语言写出正方形ABCD的性质。思考与探索: 正方形是轴对称图形吗?如果是,那么正方形有几条对称轴,并请你画出正方形的所有对称轴。矩形有两条对称轴菱形有两条对称轴正方形有四条对称轴试一试,相信你很棒!1.正方形具有而菱形不一定具有的性质是( )
A.对角线互相垂直 B.对角线互相平分
C.对角线相等 D.对角线平分一组对角C2.从四边形内能找一点,使该点到各边距离都相等的
图形可能是 ( )
A.平行四边形、矩形、菱形 B.菱形、矩形 、正方形
C.矩形、正方形 D.菱形、正方形D3.已知正方形的一条边长为2cm,则这个正方形的
周长为 ,对角线长为 ,面积为 .8cm 4.正方形的对角线和它的边所成的角是 度.45°5.已知正方形的一条对角线长为4cm,则它的边长
为 , 面积为 。6.已知正方形ABCD中,对角线AC=10cm,P为AB上任意一
点,PE⊥AC,PF⊥BD,E、F为垂足,则PE+PF= 。5cm范例分析:例1 求证:正方形的两条对角线把正方形分成四个全等的等腰直角三角形。已知:四边形ABCD是正方形,对角线AC、BD相交于O。求证:⊿ABO、⊿BCO、⊿CDO、⊿DAO是全等的等腰直角三角形证明:∵ 四边形ABCD是正方形,∴ AC=BD,AC⊥BD,AO=CO=BO=DO﹙正方形的两条对角线相等,并且互相垂直平分﹚∴⊿ABO、⊿BCO、⊿CDO、⊿DAO都是等腰直角三角形,并且⊿ABO≌⊿BCO≌⊿CDO≌⊿DAO。拓展讨论图中有多少个等腰直角三角形? ⊿ABO、⊿BCO、⊿CDO、⊿DAO、
⊿ABC、 ⊿BCD、 ⊿CDA、 ⊿DAB。练习:P112 1、2、3、归纳与小结 回顾一下,这节课我们学习了哪些内容?1、正方形的定义: 有一组邻边相等并且有一个角是直角
的平行四边形叫做正方形 正方形既是有一组邻边相等的矩形,又是有一个角是直角的菱形 2、平行四边形、矩形、菱形和正方形的关系。3正方形的性质4、正方形的周长、面积的求法。周长:C=4a设边长为a,对角线长为m作业课本第113---114 7 8 13 1.已知:如图,正方形ABCD中,E为CD边上一点,F为BC延长线上一点,CE=CF。﹙1﹚求证:⊿BCE≌⊿DCF;﹙2﹚若∠BEC=60°,求∠EFD的度数。活动与探索ABCDEF活动与探索 2.如图正方形ABCD的边长为2,E为BC的中点,P为对角线BD上的一动点。那么当P在什么位置时,CP+EP最小,最小值是多少?注:由正方形的轴对称性知道:AP=CP活动与探索ABCDEF 3.已知:如图,AC为正方形ABCD的对角线,E为AC上一点,且AB=AE,EF⊥AC交BC于F.求证:EC=EF=FB.活动与探索 4.如图正方形ABCD的边长为1,E、F分别为BC、CD上的点,且⊿CEF的周长为2,求∠EAF的度数
