9.2.3总体集中趋势的估计+9.2.4总体离散程度的估计课时作业 (含解析)
文档属性
| 名称 | 9.2.3总体集中趋势的估计+9.2.4总体离散程度的估计课时作业 (含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 189.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-10 00:00:00 | ||
图片预览



文档简介
9.2.3 总体集中趋势的估计9.2.4 总体离散程度的估计
必备知识基础练
1.学校举行演讲比赛,11位评委对甲同学《祖国,我爱你》演讲的评分情况是:
评分 7.8 8 9 9.5
评委人数 1 2 3 5
去掉一个最高分和一个最低分,则甲同学的最终得分为( )
A.8.5 B.8.9
C.9.0 D.9.1
2.我国冰雪健儿自1992年实现冬奥奖牌数0的突破,到北京冬奥会结束,共获得77块奖牌.现将1992年以来我国冬奥会获得奖牌数量统计如下表:
年份 1992 1994 1998 2002 2006 2010 2014 2018 2022
奖牌数 3 3 8 8 11 11 9 9 15
则1992年以来我国获得奖牌数的中位数为( )
A.8 B.9C.10 D.11
3.某工厂10名工人某天生产同一类型零件,生产的件数分别是10,12,14,14,15,15,16,17,17,17.记这组数据的中位数为a,平均数为b,众数为c,则( )
A.a>b>c B.b>c>a
C.c>a>b D.c>b>a
4.现有一组数据8,7,9,9,7,则这组数据的方差是( )
A.B.C.D.1
5.一组数据1,10,5,2,x,2,且2A.3 B.4C.4.5 D.5
6.(多选)某县轰轰烈烈地展开了“五好家庭”评比活动,甲、乙两村各有5户家庭进入了最后的决赛.现通过综合评比,得到这10户家庭的得分(5分制).具体得分如下表所示:
甲村得分 3.8 3.9 4.2 4.4 4.6
乙村得分 3.9 4.1 4.1 4.7 5.0
据此作出如下判断,其中正确的有( )
A.甲、乙两村最低得分均为3.9
B.甲村得分的极差为0.8
C.甲村整体水平低于乙村
D.甲村得分的中位数低于乙村
7.五个数2,2,3,3,a的平均数是3,这五个数的标准差是________.
8.为响应国家“学习强国”的号召,培养同学们的“社会主义核心价值观”,某校团委组织学生参加知识竞赛,以下数据为该校参加竞赛的10名同学的成绩:91,93,93,94,a,97,a,98,a,99.若这组数据的平均数为95,则这10名同学成绩的第80百分位数是________.
关键能力综合练
1.一组数据按从小到大的顺序排列为56,59,60,62,a,若这组数据的极差为7,则这组数据的方差为( )
A.30 B.6
C.25 D.5
2.若x1,x2,…,x2 022的平均数为2,方差为1,且yi=2xi-1,i=1,2,…,2 022, 则y1,y2,…,y2 022的平均数和方差分别为( )
A.3,2 B.3,3
C.3,4 D.4,4
3.用脚步丈量青春,用热血铸就梦想,为庆祝中国共青团成立100周年,漳州某校高中部举行“青春接力,团歌传唱”比赛,已知5位评委老师按百分制(只打整数分)分别给出某参赛班级评分,可以判断出一定有评委打满分的是( )
A.平均数为98,中位数为97
B.平均数为99,中位数为99
C.中位数为95,众数为98
D.中位数为96,极差为8
4.已知一组数据m,n,-2,1,1,3,4,6,6,7的平均数为3,则这组数据方差的最小值为( )
A.5 B.6
C.7 D.8
5.(多选)已知一组数据丢失了其中一个大于3的数据,剩下的六个数据分别是3,3,5,3,6,11,若这组数据的平均数与众数的和是中位数的2倍,则丢失的数据可能是( )
A.4 B.12
C.18 D.20
6.(多选)冬季奥林匹克运动会,是世界规模最大的冬季综合性运动会,自1924年起,每四年举办一届,第24届由中国2022年2月在北京举办,分北京赛区、延庆赛区、张家口赛区三个赛区,共15个比赛项目.为了宣传奥运精神,红星实验学校组织了甲、乙两个社团,利用一周的时间对外进行宣传,将每天宣传的次数绘制成如下频数分布折线图,则( )
A.甲社团众数小于乙社团众数
B.甲社团的平均数小于乙社团的平均数
C.甲社团的第80百分位数等于乙社团的第80百分位数
D.甲社团的方差大于乙社团的方差
7.若一组数据a1,a2,…,a8的方差为2,则3(a1-2),3(a2-2),…,3(a8-2)的标准差为________.
8.已知一组样本数据分为甲、乙两小组,其中,甲小组有10个数,其平均数为60,方差为200;乙小组有40个数,其平均数为70,方差为300,则这组样本的平均数为______,方差为________.
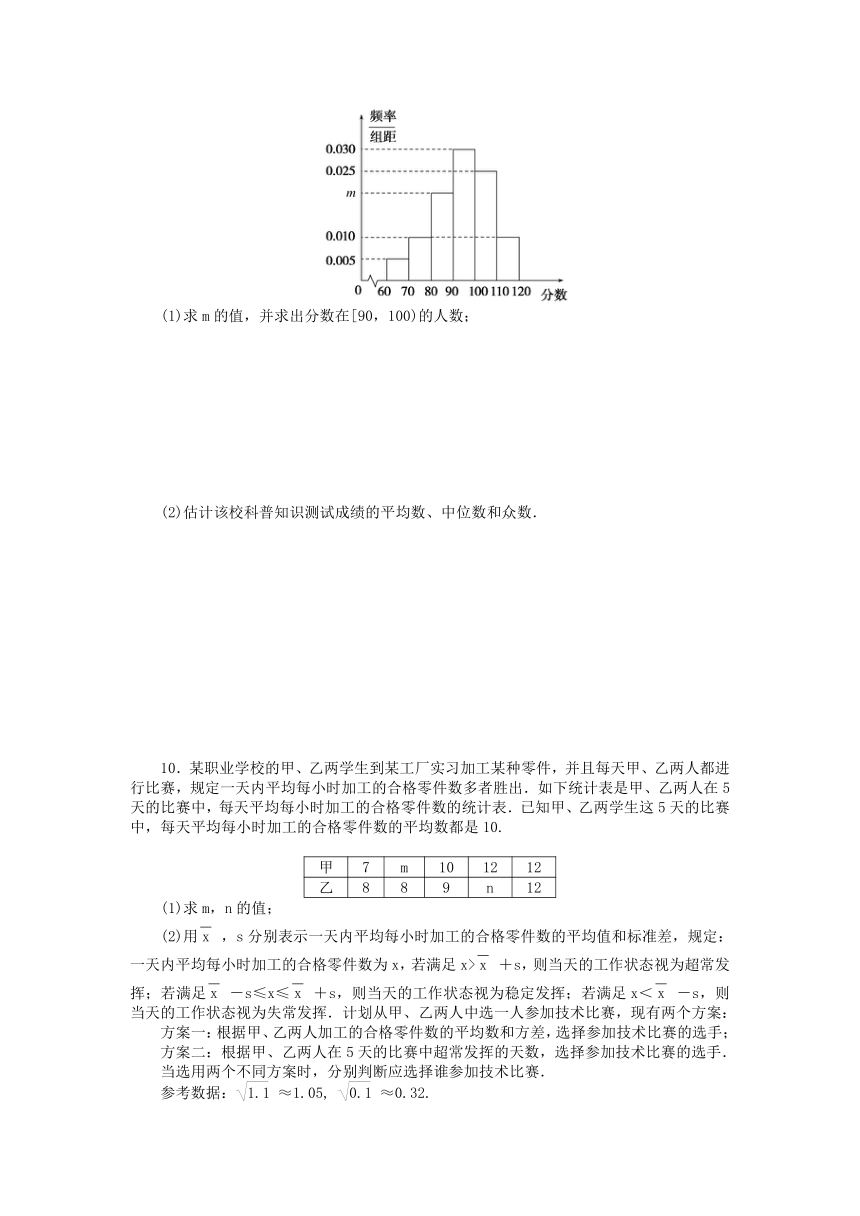
9.某学校随机抽取了100名学生通过答卷方式进行科学知识普及情况调查,试卷满分为120分.经统计得到成绩的范围是[60,120](单位:分),通过整理数据得到如下频率分布直方图:
(1)求m的值,并求出分数在[90,100)的人数;
(2)估计该校科普知识测试成绩的平均数、中位数和众数.
10.某职业学校的甲、乙两学生到某工厂实习加工某种零件,并且每天甲、乙两人都进行比赛,规定一天内平均每小时加工的合格零件数多者胜出.如下统计表是甲、乙两人在5天的比赛中,每天平均每小时加工的合格零件数的统计表.已知甲、乙两学生这5天的比赛中,每天平均每小时加工的合格零件数的平均数都是10.
甲 7 m 10 12 12
乙 8 8 9 n 12
(1)求m,n的值;
(2)用,s分别表示一天内平均每小时加工的合格零件数的平均值和标准差,规定:一天内平均每小时加工的合格零件数为x,若满足x>+s,则当天的工作状态视为超常发挥;若满足-s≤x≤+s,则当天的工作状态视为稳定发挥;若满足x<-s,则当天的工作状态视为失常发挥.计划从甲、乙两人中选一人参加技术比赛,现有两个方案:
方案一:根据甲、乙两人加工的合格零件数的平均数和方差,选择参加技术比赛的选手;
方案二:根据甲、乙两人在5天的比赛中超常发挥的天数,选择参加技术比赛的选手.
当选用两个不同方案时,分别判断应选择谁参加技术比赛.
参考数据:≈1.05, ≈0.32.
核心素养升级练
1.某零件加工厂认定工人通过试用期的方法为:随机选取试用期中的5天,再从每天生产的零件中分别随机抽取25件,要求每天合格品均不低于22件.若甲、乙、丙三人在其5天抽检样本中的合格品件数统计如下,甲:中位数为24,极差不超过2;乙:平均数为23,方差不超过1;丙:众数为23,方差不超过1,则一定能通过试用期的有( )
A.甲、乙 B.甲、丙
C.乙、丙 D.甲、乙、丙
2.(多选)已知数据x1,x2,x3,…,xn的众数、平均数、方差、第80百分位数分别是a1,b1,c1,d1,数据y1,y2,y3,…,yn的众数、平均数、方差、第80百分位数分别是a2,b2,c2,d2,且满足yi=2xi-1(i=1,2,3,…,n),则下列结论正确的是( )
A.a2=a1B.b2=2b1-1
C.c2=4c1D.d2=2d1-1
3.某单位对全体职工的某项指标进行调查.现按照性别进行分层抽样,得到男职工样本20个,其平均数和方差分别为7和4;女职工样本5个,其平均数和方差分别为8和1,以此估计总体方差为________.
9.2.3 总体集中趋势的估计
9.2.4 总体离散程度的估计
必备知识基础练
1.答案:C
解析:去掉一个最高分9.5分和一个最低分7.8分,
则甲同学的最终得分为=9.0.
故选C.
2.答案:B
解析:将自1992年以来我国冬奥会获得奖牌数从小到大排列为3,3,8,8,9,9,11,11,15,
所以1992年以来我国获得奖牌数的中位数为9.
故选B.
3.答案:C
解析:这10个数据已经从小到大进行了排序,
∴中位数a==15,众数为c=17,平均数b==14.7,
∴c>a>b.
故选C.
4.答案:C
解析:根据题意,得:=8,
则这组数据8,7,9,9,7的平均数是8,
所以这组数据的方差为×[(8-8)2+(7-8)2+(9-8)2+(9-8)2+(7-8)2]=.
故选C.
5.答案:B
解析:易得众数为2,则中位数为2×=3,将数据按照从小到大排列得1,2,2,x,5,10,则中位数为=3,解得x=4,
则平均数为×(1+2+2+4+5+10)=4.
故选B.
6.答案:BC
解析:由表中数据可知,甲村最低得分为3.8,乙村最低得分为3.9,故A选项错误;甲村得分的极差为4.6-3.8=0.8,故B选项正确;甲村整体得分为3.8+3.9+4.2+4.4+4.6=20.9,乙村整体得分为3.9+4.1+4.1+4.7+5.0=21.8,故甲村整体水平低于乙村,C选项正确;甲村得分的中位数为4.2,乙村得分的中位数4.1,故D选项错误.故选BC.
7.答案:
解析:∵=3,∴a=5,
∴标准差s==.
8.答案:97.5
解析:依题意,91+93+93+94+3a+97+98+99=95×10,解得a=95,这10名同学的成绩按从小到大依次为91,93,93,94,95,95,95,97,98,99,因10×80%=8,所以这10名同学成绩的第80百分位数是=97.5 .
关键能力综合练
1.答案:B
解析:由题意得a=56+7=63,所以这组数据的平均数为=60,方差为=6,故选B.
2.答案:C
解析:由=2,s=1 ,yi=2xi-1,可知=2-1=3 ,s=4s=4.
故选C.
3.答案:A
解析:若没有评委打满分,则总成绩sum≤99+99+97+97+97=489,平均数≤=97.8,与选项不符,所以平均数为98,中位数为97时,一定有评委打满分,A正确.
当打分结果为99,99,99,99,99时,满足平均数为99,中位数为99,所以B错误.
当打分结果为98,98,95,94,93时,满足中位数为95,众数为98,所以C错误.
当打分结果为97,97,96,95,89时,满足中位数为96,极差为8,所以D错误.
故选A.
4.答案:C
解析:由题意得m+n-2+1+1+3+4+6+6+7=3×10,得n=4-m,
所以这组数据的方差
s2=
==≥7,
所以这组数据方差的最小值为7.
故选C.
5.答案:AC
解析:设丢失的数据为x,则这七个数据的平均数为,众数是3,
若3若x≥5,则中位数为5,此时+3=2×5,解得x=18.
综上所述,丢失的数据可能是4,18.
故选AC.
6.答案:ACD
解析:甲社团众数为2,乙社团众数为3,所以A正确;
甲的平均数为(2+2+3+2+5+4+3)=3,
乙的平均数为(2+2+3+4+3+3+4)=3,所以平均数相等,所以B错误;
甲社团数据从小到大排列为2、2、2、3、3、4、5,其中7×80%=5.6,
所以甲社团的第80百分位数为4,同理可得乙社团的第80百分位数为4,所以C正确;
甲社团的方差为[3(2-3)2+(4-3)2+(5-3)2]=,
乙社团的方差为[2(2-3)2+2(4-3)2]=,
故甲社团的方差大于乙社团的方差,D正确.
故选ACD.
7.答案:3
解析:因为一组数据a1,a2,…,a8的方差为2,
所以3(a1-2),3(a2-2),…,3(a8-2)的方差为32×2=18,所以其标准差为3.
8.答案:68 296
解析:=×60+×70=68,
s2=[200+(68-60)2]+[300+(70-68)2]=296.
9.解析:(1)由频率分布直方图得:
m==0.02;
分数在[90,100)对应频率为0.03×10=0.3,100×0.3=30,
所以分数在[90,100)的人数为30人.
(2)依题意,65×0.05+75×0.1+85×0.2+95×0.3+105×0.25+115×0.1=94,
所以成绩平均数为94分;
因0.05+0.1+0.2=0.35,0.05+0.1+0.2+0.3=0.65,
则成绩的中位数在90分到100分之间,设成绩的中位数为x分,
由0.05+0.1+0.2+0.03×(x-90)=0.5,解得x=95,
所以成绩的中位数为95分;
因成绩在[90,100)的频率最大,而=95,所以成绩的众数为95分.
10.解析:(1)由题设知,可得
(2)方案一:由题设知甲乙的平均数为10,甲的方差s=×[(7-10)2+(9-10)2+(10-10)2+(12-10)2+(12-10)2]=,
乙的方差s=×[(8-10)2+(8-10)2+(9-10)2+(13-10)2+(12-10)2]=,∴s故应选择甲参加技术比赛;
方案二:由上知s1=6≈1.92,s2=2≈2.1,对于甲大于+s1=11.92的天数为2天;
对于乙大于+s2=12.1的天数为1天;∴应选择甲参加技术比赛.
核心素养升级练
1.答案:A
解析:对于甲:由甲的统计数据可知,甲至少有3天的合格品数不低于24,最低合格品数不低于22,所以甲一定能通过;
对于乙:设乙每天的合格品件数为ai(i=1,2,3,4,5),ai∈Z,则≤1,
即(ai-23)2≤5.若乙有不止一天的合格品数低于22,(ai-23)2>5,不合题意;
若乙只有一天的合格品数低于22,不妨取a1=21,(a1-23)2=4,因为平均数为23,则至少有一天的合格品数为25或至少有两天的合格品数为24,无论哪种情况,都可以得到 (ai-23)2>5,不合题意,所以乙的每一天的合格品数都不低于22,乙一定能通过;
对于丙:若丙的合格品数为21,22,23,23,23,则丙的众数为23,方差为0.64,符合丙的统计数据,但丙不能通过;
所以甲、乙一定能通过,A正确.
故选A.
2.答案:BCD
解析:由题意可知,两组数据满足yi=2xi-1(i=1,2,3,…,n),则它们的众数也满足该关系,则有a2=2a1-1,故A错误;
由平均数计算公式得:
=
=2×-1 ,即b2=2b1-1,故B正确;
由方差的性质可得c2=4c1,故C正确;
对于数据x1,x2,x3,…,xn,假设其第80百分位数为d1,
当0.8n=k是整数时,d1= ,当0.8n不是整数时,设其整数部分为k,则d1=xk+1,
故对于数据2x1-1,2x2-1,2x3-1,…,2xn-1,假设其第80百分位数为d2,
当0.8n=k是整数时,d2==2d1-1,当0.8n不是整数时,设其整数部分为k,则d2=2xk+1-1=2d1-1,
故d2=2d1-1,故D正确.
故选BCD.
3.答案:3.56
解析:设男职工的指标数分别为x1,x2,…,x20,女职工的指标数分别为y1,y2,…,y5,
所以本次调查的总样本的平均数为
本次调查的总样本的方差是
必备知识基础练
1.学校举行演讲比赛,11位评委对甲同学《祖国,我爱你》演讲的评分情况是:
评分 7.8 8 9 9.5
评委人数 1 2 3 5
去掉一个最高分和一个最低分,则甲同学的最终得分为( )
A.8.5 B.8.9
C.9.0 D.9.1
2.我国冰雪健儿自1992年实现冬奥奖牌数0的突破,到北京冬奥会结束,共获得77块奖牌.现将1992年以来我国冬奥会获得奖牌数量统计如下表:
年份 1992 1994 1998 2002 2006 2010 2014 2018 2022
奖牌数 3 3 8 8 11 11 9 9 15
则1992年以来我国获得奖牌数的中位数为( )
A.8 B.9C.10 D.11
3.某工厂10名工人某天生产同一类型零件,生产的件数分别是10,12,14,14,15,15,16,17,17,17.记这组数据的中位数为a,平均数为b,众数为c,则( )
A.a>b>c B.b>c>a
C.c>a>b D.c>b>a
4.现有一组数据8,7,9,9,7,则这组数据的方差是( )
A.B.C.D.1
5.一组数据1,10,5,2,x,2,且2
6.(多选)某县轰轰烈烈地展开了“五好家庭”评比活动,甲、乙两村各有5户家庭进入了最后的决赛.现通过综合评比,得到这10户家庭的得分(5分制).具体得分如下表所示:
甲村得分 3.8 3.9 4.2 4.4 4.6
乙村得分 3.9 4.1 4.1 4.7 5.0
据此作出如下判断,其中正确的有( )
A.甲、乙两村最低得分均为3.9
B.甲村得分的极差为0.8
C.甲村整体水平低于乙村
D.甲村得分的中位数低于乙村
7.五个数2,2,3,3,a的平均数是3,这五个数的标准差是________.
8.为响应国家“学习强国”的号召,培养同学们的“社会主义核心价值观”,某校团委组织学生参加知识竞赛,以下数据为该校参加竞赛的10名同学的成绩:91,93,93,94,a,97,a,98,a,99.若这组数据的平均数为95,则这10名同学成绩的第80百分位数是________.
关键能力综合练
1.一组数据按从小到大的顺序排列为56,59,60,62,a,若这组数据的极差为7,则这组数据的方差为( )
A.30 B.6
C.25 D.5
2.若x1,x2,…,x2 022的平均数为2,方差为1,且yi=2xi-1,i=1,2,…,2 022, 则y1,y2,…,y2 022的平均数和方差分别为( )
A.3,2 B.3,3
C.3,4 D.4,4
3.用脚步丈量青春,用热血铸就梦想,为庆祝中国共青团成立100周年,漳州某校高中部举行“青春接力,团歌传唱”比赛,已知5位评委老师按百分制(只打整数分)分别给出某参赛班级评分,可以判断出一定有评委打满分的是( )
A.平均数为98,中位数为97
B.平均数为99,中位数为99
C.中位数为95,众数为98
D.中位数为96,极差为8
4.已知一组数据m,n,-2,1,1,3,4,6,6,7的平均数为3,则这组数据方差的最小值为( )
A.5 B.6
C.7 D.8
5.(多选)已知一组数据丢失了其中一个大于3的数据,剩下的六个数据分别是3,3,5,3,6,11,若这组数据的平均数与众数的和是中位数的2倍,则丢失的数据可能是( )
A.4 B.12
C.18 D.20
6.(多选)冬季奥林匹克运动会,是世界规模最大的冬季综合性运动会,自1924年起,每四年举办一届,第24届由中国2022年2月在北京举办,分北京赛区、延庆赛区、张家口赛区三个赛区,共15个比赛项目.为了宣传奥运精神,红星实验学校组织了甲、乙两个社团,利用一周的时间对外进行宣传,将每天宣传的次数绘制成如下频数分布折线图,则( )
A.甲社团众数小于乙社团众数
B.甲社团的平均数小于乙社团的平均数
C.甲社团的第80百分位数等于乙社团的第80百分位数
D.甲社团的方差大于乙社团的方差
7.若一组数据a1,a2,…,a8的方差为2,则3(a1-2),3(a2-2),…,3(a8-2)的标准差为________.
8.已知一组样本数据分为甲、乙两小组,其中,甲小组有10个数,其平均数为60,方差为200;乙小组有40个数,其平均数为70,方差为300,则这组样本的平均数为______,方差为________.
9.某学校随机抽取了100名学生通过答卷方式进行科学知识普及情况调查,试卷满分为120分.经统计得到成绩的范围是[60,120](单位:分),通过整理数据得到如下频率分布直方图:
(1)求m的值,并求出分数在[90,100)的人数;
(2)估计该校科普知识测试成绩的平均数、中位数和众数.
10.某职业学校的甲、乙两学生到某工厂实习加工某种零件,并且每天甲、乙两人都进行比赛,规定一天内平均每小时加工的合格零件数多者胜出.如下统计表是甲、乙两人在5天的比赛中,每天平均每小时加工的合格零件数的统计表.已知甲、乙两学生这5天的比赛中,每天平均每小时加工的合格零件数的平均数都是10.
甲 7 m 10 12 12
乙 8 8 9 n 12
(1)求m,n的值;
(2)用,s分别表示一天内平均每小时加工的合格零件数的平均值和标准差,规定:一天内平均每小时加工的合格零件数为x,若满足x>+s,则当天的工作状态视为超常发挥;若满足-s≤x≤+s,则当天的工作状态视为稳定发挥;若满足x<-s,则当天的工作状态视为失常发挥.计划从甲、乙两人中选一人参加技术比赛,现有两个方案:
方案一:根据甲、乙两人加工的合格零件数的平均数和方差,选择参加技术比赛的选手;
方案二:根据甲、乙两人在5天的比赛中超常发挥的天数,选择参加技术比赛的选手.
当选用两个不同方案时,分别判断应选择谁参加技术比赛.
参考数据:≈1.05, ≈0.32.
核心素养升级练
1.某零件加工厂认定工人通过试用期的方法为:随机选取试用期中的5天,再从每天生产的零件中分别随机抽取25件,要求每天合格品均不低于22件.若甲、乙、丙三人在其5天抽检样本中的合格品件数统计如下,甲:中位数为24,极差不超过2;乙:平均数为23,方差不超过1;丙:众数为23,方差不超过1,则一定能通过试用期的有( )
A.甲、乙 B.甲、丙
C.乙、丙 D.甲、乙、丙
2.(多选)已知数据x1,x2,x3,…,xn的众数、平均数、方差、第80百分位数分别是a1,b1,c1,d1,数据y1,y2,y3,…,yn的众数、平均数、方差、第80百分位数分别是a2,b2,c2,d2,且满足yi=2xi-1(i=1,2,3,…,n),则下列结论正确的是( )
A.a2=a1B.b2=2b1-1
C.c2=4c1D.d2=2d1-1
3.某单位对全体职工的某项指标进行调查.现按照性别进行分层抽样,得到男职工样本20个,其平均数和方差分别为7和4;女职工样本5个,其平均数和方差分别为8和1,以此估计总体方差为________.
9.2.3 总体集中趋势的估计
9.2.4 总体离散程度的估计
必备知识基础练
1.答案:C
解析:去掉一个最高分9.5分和一个最低分7.8分,
则甲同学的最终得分为=9.0.
故选C.
2.答案:B
解析:将自1992年以来我国冬奥会获得奖牌数从小到大排列为3,3,8,8,9,9,11,11,15,
所以1992年以来我国获得奖牌数的中位数为9.
故选B.
3.答案:C
解析:这10个数据已经从小到大进行了排序,
∴中位数a==15,众数为c=17,平均数b==14.7,
∴c>a>b.
故选C.
4.答案:C
解析:根据题意,得:=8,
则这组数据8,7,9,9,7的平均数是8,
所以这组数据的方差为×[(8-8)2+(7-8)2+(9-8)2+(9-8)2+(7-8)2]=.
故选C.
5.答案:B
解析:易得众数为2,则中位数为2×=3,将数据按照从小到大排列得1,2,2,x,5,10,则中位数为=3,解得x=4,
则平均数为×(1+2+2+4+5+10)=4.
故选B.
6.答案:BC
解析:由表中数据可知,甲村最低得分为3.8,乙村最低得分为3.9,故A选项错误;甲村得分的极差为4.6-3.8=0.8,故B选项正确;甲村整体得分为3.8+3.9+4.2+4.4+4.6=20.9,乙村整体得分为3.9+4.1+4.1+4.7+5.0=21.8,故甲村整体水平低于乙村,C选项正确;甲村得分的中位数为4.2,乙村得分的中位数4.1,故D选项错误.故选BC.
7.答案:
解析:∵=3,∴a=5,
∴标准差s==.
8.答案:97.5
解析:依题意,91+93+93+94+3a+97+98+99=95×10,解得a=95,这10名同学的成绩按从小到大依次为91,93,93,94,95,95,95,97,98,99,因10×80%=8,所以这10名同学成绩的第80百分位数是=97.5 .
关键能力综合练
1.答案:B
解析:由题意得a=56+7=63,所以这组数据的平均数为=60,方差为=6,故选B.
2.答案:C
解析:由=2,s=1 ,yi=2xi-1,可知=2-1=3 ,s=4s=4.
故选C.
3.答案:A
解析:若没有评委打满分,则总成绩sum≤99+99+97+97+97=489,平均数≤=97.8,与选项不符,所以平均数为98,中位数为97时,一定有评委打满分,A正确.
当打分结果为99,99,99,99,99时,满足平均数为99,中位数为99,所以B错误.
当打分结果为98,98,95,94,93时,满足中位数为95,众数为98,所以C错误.
当打分结果为97,97,96,95,89时,满足中位数为96,极差为8,所以D错误.
故选A.
4.答案:C
解析:由题意得m+n-2+1+1+3+4+6+6+7=3×10,得n=4-m,
所以这组数据的方差
s2=
==≥7,
所以这组数据方差的最小值为7.
故选C.
5.答案:AC
解析:设丢失的数据为x,则这七个数据的平均数为,众数是3,
若3
综上所述,丢失的数据可能是4,18.
故选AC.
6.答案:ACD
解析:甲社团众数为2,乙社团众数为3,所以A正确;
甲的平均数为(2+2+3+2+5+4+3)=3,
乙的平均数为(2+2+3+4+3+3+4)=3,所以平均数相等,所以B错误;
甲社团数据从小到大排列为2、2、2、3、3、4、5,其中7×80%=5.6,
所以甲社团的第80百分位数为4,同理可得乙社团的第80百分位数为4,所以C正确;
甲社团的方差为[3(2-3)2+(4-3)2+(5-3)2]=,
乙社团的方差为[2(2-3)2+2(4-3)2]=,
故甲社团的方差大于乙社团的方差,D正确.
故选ACD.
7.答案:3
解析:因为一组数据a1,a2,…,a8的方差为2,
所以3(a1-2),3(a2-2),…,3(a8-2)的方差为32×2=18,所以其标准差为3.
8.答案:68 296
解析:=×60+×70=68,
s2=[200+(68-60)2]+[300+(70-68)2]=296.
9.解析:(1)由频率分布直方图得:
m==0.02;
分数在[90,100)对应频率为0.03×10=0.3,100×0.3=30,
所以分数在[90,100)的人数为30人.
(2)依题意,65×0.05+75×0.1+85×0.2+95×0.3+105×0.25+115×0.1=94,
所以成绩平均数为94分;
因0.05+0.1+0.2=0.35,0.05+0.1+0.2+0.3=0.65,
则成绩的中位数在90分到100分之间,设成绩的中位数为x分,
由0.05+0.1+0.2+0.03×(x-90)=0.5,解得x=95,
所以成绩的中位数为95分;
因成绩在[90,100)的频率最大,而=95,所以成绩的众数为95分.
10.解析:(1)由题设知,可得
(2)方案一:由题设知甲乙的平均数为10,甲的方差s=×[(7-10)2+(9-10)2+(10-10)2+(12-10)2+(12-10)2]=,
乙的方差s=×[(8-10)2+(8-10)2+(9-10)2+(13-10)2+(12-10)2]=,∴s
方案二:由上知s1=6≈1.92,s2=2≈2.1,对于甲大于+s1=11.92的天数为2天;
对于乙大于+s2=12.1的天数为1天;∴应选择甲参加技术比赛.
核心素养升级练
1.答案:A
解析:对于甲:由甲的统计数据可知,甲至少有3天的合格品数不低于24,最低合格品数不低于22,所以甲一定能通过;
对于乙:设乙每天的合格品件数为ai(i=1,2,3,4,5),ai∈Z,则≤1,
即(ai-23)2≤5.若乙有不止一天的合格品数低于22,(ai-23)2>5,不合题意;
若乙只有一天的合格品数低于22,不妨取a1=21,(a1-23)2=4,因为平均数为23,则至少有一天的合格品数为25或至少有两天的合格品数为24,无论哪种情况,都可以得到 (ai-23)2>5,不合题意,所以乙的每一天的合格品数都不低于22,乙一定能通过;
对于丙:若丙的合格品数为21,22,23,23,23,则丙的众数为23,方差为0.64,符合丙的统计数据,但丙不能通过;
所以甲、乙一定能通过,A正确.
故选A.
2.答案:BCD
解析:由题意可知,两组数据满足yi=2xi-1(i=1,2,3,…,n),则它们的众数也满足该关系,则有a2=2a1-1,故A错误;
由平均数计算公式得:
=
=2×-1 ,即b2=2b1-1,故B正确;
由方差的性质可得c2=4c1,故C正确;
对于数据x1,x2,x3,…,xn,假设其第80百分位数为d1,
当0.8n=k是整数时,d1= ,当0.8n不是整数时,设其整数部分为k,则d1=xk+1,
故对于数据2x1-1,2x2-1,2x3-1,…,2xn-1,假设其第80百分位数为d2,
当0.8n=k是整数时,d2==2d1-1,当0.8n不是整数时,设其整数部分为k,则d2=2xk+1-1=2d1-1,
故d2=2d1-1,故D正确.
故选BCD.
3.答案:3.56
解析:设男职工的指标数分别为x1,x2,…,x20,女职工的指标数分别为y1,y2,…,y5,
所以本次调查的总样本的平均数为
本次调查的总样本的方差是
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
