9.2.2总体百分位数的估计 课时作业(含解析)
文档属性
| 名称 | 9.2.2总体百分位数的估计 课时作业(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 676.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-10 00:00:00 | ||
图片预览



文档简介
9.2.1 总体取值规律的估计9.2.2 总体百分位数的估计
必备知识基础练
1.某股票近10个交易日的价格见下表.
天数 1 2 3 4 5 6 7 8 9 10
股价/元 4.32 4.18 4.28 4.34 4.30 4.45 4.51 4.48 4.52 4.55
下列统计图中,表示上面的数据较合适的是( )
A.频数直方图 B.扇形统计图
C.折线统计图 D.条形统计图
2.二十四节气是中国劳动人民长期经验积累的结晶,它与白昼时长密切相关.当春分、秋分时,昼夜时长大致相等;当夏至时,白昼时长最长.根据下图,在下列选项中白昼时长低于11小时的节气是( )
A.惊蛰 B.小满
C.立秋 D.大寒
3.甲、乙两所学校的男女生比例如图所示,已知甲校学生总数为1 500,乙校学生总数为1 000,下列结论错误的是( )
A.甲校女生比乙校女生多
B.乙校男生比甲校男生少
C.乙校女生比甲校男生少
D.甲校女生比乙校男生少
4.为了解学生在“弘扬传统文化,品读经典文学”月的阅读情况,现从全校学生中随机抽取了部分学生,并统计了他们的阅读时间(阅读时间t∈[0,50]),分组整理数据得到如图所示的频率分布直方图.则图中a的值为( )
A.0.028 B.0.029
C.0.280 D.0.290
5.某射击运动员6次的训练成绩分别为:80,82,89,90,91,86,则这6次成绩的第80百分位数为( )
A.89 B.89.5
C.90 D.91
6.某校1 000名学生的高中历史学业水平考试成绩的频率直方图如图所示,规定90分及以上为优秀等级,则该校学生优秀等级的人数为( )
A.15 B.30
C.150 D.300
7.有一个容量为100的样本,数据分组及各组的频数如下:[12,15),5;[15,18),17;[18,21),17;[21,24),23;[24,27),19;[27,30),11;[30,33],8.则样本数据落在[21,30)内的频率为________.
8.河北省九大高峰按照海拔(单位:米)排名依次为小五台山(2 882)、驼梁山(2 281)、雾灵山(2 118)、长城岭(2 100)、白石山(2 096)、野三坡(1 983)、祖山(1 428)、天桂山(1 270)、狼牙山(1 105),则这九大高峰的海拔数据的第70百分位数为________.
关键能力综合练
1.为了了解某外贸企业职工对“一带一路”的认知程度,随机抽取了110名职工组织了“一带一路”知识竞赛.满分为100分(80分及以上为认知程度较高).并将所得成绩分组得到了如图所示的频率分布折线图.从频率分布折线图中得到的这110名职工成绩的信息正确的是( )
A.成绩是100分的人数比成绩是50分的人数多
B.对“一带一路”认知程度较高的人数是35
C.成绩是75分的人数为40
D.成绩落在[70,80)内的人数为20
2.某居民小区户主人数和户主对户型结构的满意率如图(1)和图(2)所示,为了解该小区户主对户型结构的满意程度,用比例分配的分层随机抽样方法抽取25%的户主作为样本进行调查,则样本容量和抽取的户主对四居室满意的人数分别为( )
A.200,16 B.200,18
C.240,16 D.240,18
3.某班同学进行社会实践,对年龄(单位:岁)在[25,55]内的人群随机抽取几人进行了生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率直方图,则下表中p,a的值分别为( )
组数 分组 低碳族的人数 占本组的频率
第一组 [25,30) 120 0.6
第二组 [30,35) 195 p
第三组 [35,40) 100 0.5
第四组 [40,45) a 0.4
第五组 [45,50) 30 0.3
第六组 [50,55] 15 0.3
A.0.79,20 B.0.195,40
C.0.65,60 D.0.975,80
4.为了鼓励学生积极锻炼身体,强健体魄,某学校决定每学期对体育成绩在年级前100名的学生给予专项奖励.已知该校高三年级共有500名学生,如图是该年级学生本学期体育测试成绩的频率分布直方图.据此估计,能够获得该项奖励的高三学生的最低分数为( )
A.89 B.88
C.87 D.86
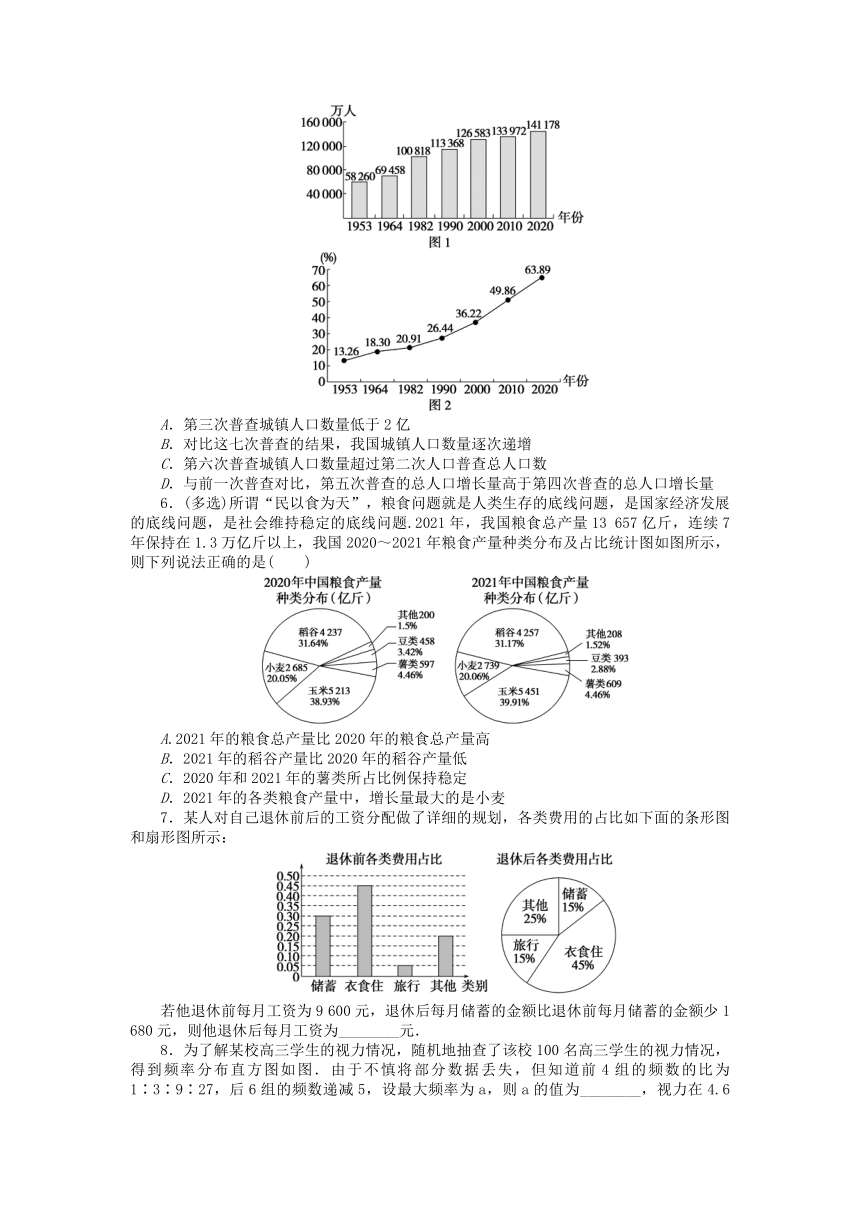
5.(多选)新中国成立以来,我国一共进行了七次全国人口普查(以下简称“普查”),历次普查得到的全国人口总数如图1所示,城镇人口比重如图2所示.下列结论正确的是( )
A.第三次普查城镇人口数量低于2亿
B.对比这七次普查的结果,我国城镇人口数量逐次递增
C.第六次普查城镇人口数量超过第二次人口普查总人口数
D.与前一次普查对比,第五次普查的总人口增长量高于第四次普查的总人口增长量
6.(多选)所谓“民以食为天”,粮食问题就是人类生存的底线问题,是国家经济发展的底线问题,是社会维持稳定的底线问题.2021年,我国粮食总产量13 657亿斤,连续7年保持在1.3万亿斤以上,我国2020~2021年粮食产量种类分布及占比统计图如图所示,则下列说法正确的是( )
A.2021年的粮食总产量比2020年的粮食总产量高
B.2021年的稻谷产量比2020年的稻谷产量低
C.2020年和2021年的薯类所占比例保持稳定
D.2021年的各类粮食产量中,增长量最大的是小麦
7.某人对自己退休前后的工资分配做了详细的规划,各类费用的占比如下面的条形图和扇形图所示:
若他退休前每月工资为9 600元,退休后每月储蓄的金额比退休前每月储蓄的金额少1 680元,则他退休后每月工资为________元.
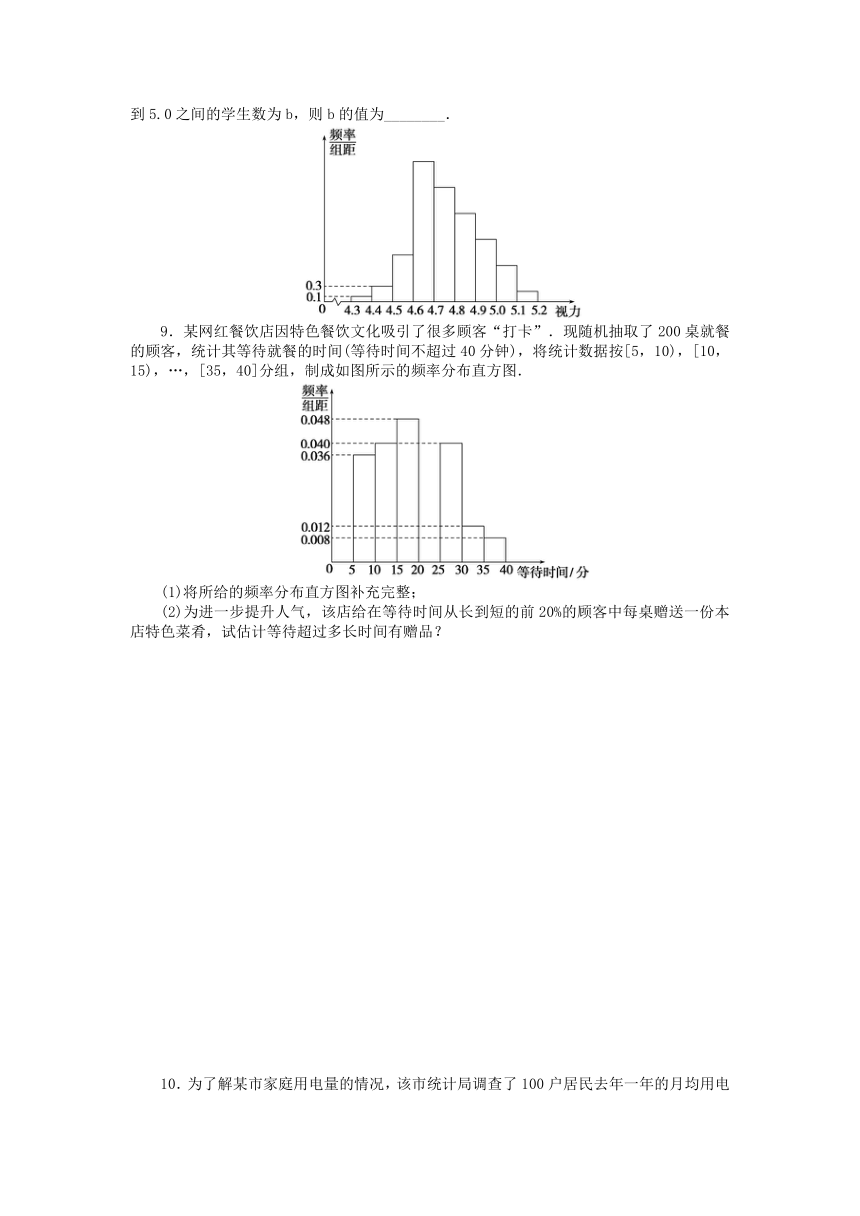
8.为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图如图.由于不慎将部分数据丢失,但知道前4组的频数的比为1∶3∶9∶27,后6组的频数递减5,设最大频率为a,则a的值为________,视力在4.6到5.0之间的学生数为b,则b的值为________.
9.某网红餐饮店因特色餐饮文化吸引了很多顾客“打卡”.现随机抽取了200桌就餐的顾客,统计其等待就餐的时间(等待时间不超过40分钟),将统计数据按[5,10),[10,15),…,[35,40]分组,制成如图所示的频率分布直方图.
(1)将所给的频率分布直方图补充完整;
(2)为进一步提升人气,该店给在等待时间从长到短的前20%的顾客中每桌赠送一份本店特色菜肴,试估计等待超过多长时间有赠品?
10.为了解某市家庭用电量的情况,该市统计局调查了100户居民去年一年的月均用电量,发现他们的用电量都在50 kW·h至350 kW·h之间,进行适当分组后,画出频率分布直方图如图所示.
(1)求a的值;
(2)求被调查用户中,用电量大于200 kW·h的户数;
(3)为了既满足居民的基本用电需求,又提高能源的利用效率,市政府计划采用阶梯定价,希望使85%的居民缴费在第一档(费用最低),请给出第一档用电标准(单位:kW·h)的建议,并简要说明理由.
核心素养升级练
1.郑州市某家保险公司的保险产品有以下五种:甲,一年期短险;乙,两全保险;丙,理财类保险;丁,定期寿险;戊,重大疾病保险.各种保险按相关约定进行参保与理赔,该保险公司对五个险种的参保客户进行抽样调查,得到如图所示的统计图,则以下四个说法中正确的是( )
A.42~53周岁客户人数是不低于54周岁的客户人数的4倍多
B.不低于54周岁客户参保总费用最多
C.丁险种人均参保费用最低
D.戊险种参保人都是42~53周岁的客户
2.某市教育局为了解疫情时期网络教学期间的学生学习情况,从该市随机抽取了1 000名高中学生,对他们每天的平均学习时间进行问卷调查,根据所得信息制作了如图所示的频率分布直方图,根据此图,估计该市高中学生每天的平均学习时间的60%分位数为________小时.
3.某大学艺术专业400名学生参加某次测评,根据男女学生人数比例、使用分层随机抽样的方法从中随机抽取了100名学生,记录他们的分数、将数据分成7组:[20,30),[30,40),…,[80,90],并整理得到如图的频率分布直方图.
(1)估计总体400名学生中分数小于60的人数;
(2)已知样本中分数小于40的学生有5人,试估计总体中分数在区间[40,50)内的人数;
(3)根据该大学规定,把25%的学生划定为不及格,确定本次测试的及格分数线,低于及格分数线的学生需要补考.
9.2.1 总体取值规律的估计
9.2.2 总体百分位数的估计
必备知识基础练
1.答案:C
解析:根据每种统计图的概念可知,折线图能有效地表示出每天的股价波动情况和趋势,我们能比较直观地看出此股票在这10天中,其价格总体趋势,也可以看出每天的变化,
∴用折线图表示不断变化的数据,是有优越性的.
故选C.
2.答案:D
解析:根据统计图可得惊蛰、小满、立秋的白昼时长大于11小时,
大寒节气的白昼时长低于11小时.
故选D.
3.答案:D
解析:甲校男生和女生的人数均为750,乙校男生人数为400,女生人数为600.
所以甲校女生比乙校女生多,故A正确;乙校男生比甲校男生少,故B正确;乙校女生比甲校男生少,故C正确;甲校女生比乙校男生多,故D错误.
故选D.
4.答案:A
解析:由(0.006+a+0.040+0.020+0.006)×10=1得a=0.028.
故选A.
5.答案:C
解析:该运动员6次的训练成绩从小到大排列为:80,82,86,89,90,91.
由6×80%=4.8,可得第80百分位数为从小到大排列的数据中的第5个数据,即90.
故选C.
6.答案:C
解析:根据频率直方图得该校学生优秀等级的概率是0.015×10=0.15,
故该校学生优秀等级的人数是1 000×0.15=150.
故选C.
7.答案:0.53
解析:依题意,样本数据落在[21,30)内的数据个数为:23+19+11=53,
所以样本数据落在[21,30)内的频率为=0.53.
8.答案:2 118
解析:将这九大高峰的海拔数据按照从小到大的顺序排列,依次为1 105,1 270,1 428,1 983,2 096,2 100,2 118,2 281,2 882,因为70%×9=6.3,所以第70百分位数为第7项数据,即2 118.
关键能力综合练
1.答案:C
解析:对于A,由于频率分布折线图表示的是某一个范围的频率,所以从频率分布折线图看不出成绩是100分的人数比成绩是50分的人数多,所以A错误;对于B,成绩为80分及以上的职工人数为×10×110=40,所以B错误;对于C,由题意可得成绩是75分的人数为110××10=40,故C正确;
对于D,成绩落在[70,80)内的人数为×10×110=40,D错误.
故选C.
2.答案:A
解析:由图(1)得该小区户主总人数为240+400+160=800(人),
所以样本容量为800×25%=200(人),
其中四居室户主有160×25%=40(人),
由图(2)得抽取的户主中对四居室满意的有40×40%=16(人).
故选A.
3.答案:C
解析:第一组人数为120÷0.6=200,第三组人数为100÷0.5=200,第五组人数为30÷0.3=100,第六组人数为15÷0.3=50,
由题中的频率直方图可得第一组频率为5×0.04=0.2,所以n==1 000,
所以第四组人数为5×0.03×1 000=150,所以a=150×0.4=60,
第二组人数为1 000-(200+200+150+100+50)=300,所以p==0.65.
故选C.
4.答案:B
解析:由题意,=0.2,[90,95)的频率为0.02×5=0.1,[85,90)的频率为0.05×5=0.25,则0.1<0.2<0.25,则第100名在[85,90)中,设分数为x,[x,90)的频率为0.2-0.1=0.1,所以=== x=88.
故选B.
5.答案:BD
解析:A:第三次普查城镇人口数量100 818×20.91%=21 081.043 8万人,即大于2亿,错误;B:各次普查总人口数逐年递增,同时城镇人口比重也逐年递增,故我国城镇人口数量逐次递增,正确;C:第六次普查城镇人口数量133 972×49.86%=66 798.439 2万人,而第二次人口普查总人口数为69 458万人,第六次普查城镇人口数量未超过第二次人口普查总人口数,错误;D:第五次普查的总人口增长量126 583-113 368=13 215万人,第四次普查的总人口增长量113 368-100 818=12 550万人,正确.
故选BD.
6.答案:AC
解析:2020年的粮食总产量为4 237+5 213+2 685+200+458+597=13 390亿斤,2021年的粮食总产量为4 257+5 451+2 739+208+393+609=13 657亿斤,因为13 657>13 390,故A正确;因为4 257>4 237,所以2021年的稻谷产量比2020年的稻谷产量高,故B错误;2020年和2021年的薯类所占比例都为4.46%,故C正确;
由统计图可得2021年的各类粮食产量中,增长量最大的是玉米,故D错误.
故选AC.
7.答案:8 000
解析:退休前每月储蓄的金额为9 600×0.30=2 880元,
退休后每月储蓄的金额为2 880-1 680=1 200元,
退休后每月工资为1 200÷0.15=8 000元.
8.答案:0.27 78
解析:设第1组的频数为x,则前4组的频数分别为x,3x,9x,27x,后5组的频数为27x-5,27x-10,27x-15,27x-20,27x-25,由题意得x+3x+9x+27x+(27x-5)+…+27x-25=100,即175x-75=100,解得x=1,
故a=0.27,b=78.
9.解析:(1)因为1-(0.036×5+0.04×5+0.048×5+0.04×5+0.012×5+0.008×5)=0.08,又0.08÷5=0.016,
所以频率分布直方图补充完整为
(2)设估计等待x分钟以上的顾客可以获得赠品,
由题意,0.008×5+0.012×5+(30-x)×0.04=0.2,解得x=27.5,
所以估计等待27分钟以上的顾客可以获得赠品.
10.解析:(1)因为(0.002 4+0.003 6+a+0.004 4+0.002 4+0.001 2)×50=1,所以a=0.006.
(2)根据频率分布直方图可知:“用电量大于200 kW·h”的频率为(0.004 4+0.002 4+0.001 2)×50=0.4,
所以用电量大于200 kW·h的户数为:100×0.4=40,
故用电量大于200 kW·h有40户;
(3)因为前四组的频率和为:(0.002 4+0.003 6+0.006+0.004 4)×50=0.82<0.85,
前五组的频率之和为(0.002 4+0.003 6+0.006+0.004 4+0.002 4)×50=0.94>0.85,
所以频率为0.85时对应的数据在第五组,
所以第一档用电标准为250+=262.5 kW·h.
故第一档用电标准为262.5 kW·h.
核心素养升级练
1.答案:A
解析:对观察参保人年龄分布的扇形图,42~53周岁客户人数占比33%,不低于54周岁的客户人数占比8%,42~53周岁客户人数是不低于54周岁的客户人数的4倍多,故A正确;统计图显示的是人均参保费用,由于人数未知,故不能确定哪个年龄段参保总费用最多,故B错误;由参保险种比例,丁险种参保比例最高,但统计图看不出丁险种的人均参保费用,故C错误;戊险种的参保人占比33%,42~53周岁客户人数占比33%,但统计图看不出两者相同,故D错误.
故选A.
2.答案:9.2
解析:由频率分布直方图可知,高中学生每天的平均学习时间的60%分位数在第3组,设其为x小时,则
0.05×2+0.10×2+0.25(x-8)=0.6,
解得x=9.2,
所以该市高中学生每天的平均学习时间的60%分位数约为9.2小时.
3.解析:(1)据频率分布直方图可知,样本中分数不小于60的频率为(0.02+0.04+0.02)×10=0.8,所以样本中分数小于60的频率为1-0.8=0.2,
所以估计总体400名学生中分数小于60的人数为400×0.2=80.
(2)根据题意,样本中分数不小于50的频率为(0.01+0.02+0.04+0.02)×10=0.9,
分数在区间[40,50)内的人数为100-100×0.9-5=5,
所以总体中分数在区间[40,50)内的人数估计为400×=20.
(3)设分数的第25百分位数为x,
分数小于70的频率为1-(0.04+0.02)×10=0.4,
分数小于60的频率为1-(0.02+0.04+0.02)×10=0.2,
所以x∈[60,70),即0.2+(x-60)×0.02=0.25,解得x=62.5,
则本次考试的及格分数线为62.5分.
必备知识基础练
1.某股票近10个交易日的价格见下表.
天数 1 2 3 4 5 6 7 8 9 10
股价/元 4.32 4.18 4.28 4.34 4.30 4.45 4.51 4.48 4.52 4.55
下列统计图中,表示上面的数据较合适的是( )
A.频数直方图 B.扇形统计图
C.折线统计图 D.条形统计图
2.二十四节气是中国劳动人民长期经验积累的结晶,它与白昼时长密切相关.当春分、秋分时,昼夜时长大致相等;当夏至时,白昼时长最长.根据下图,在下列选项中白昼时长低于11小时的节气是( )
A.惊蛰 B.小满
C.立秋 D.大寒
3.甲、乙两所学校的男女生比例如图所示,已知甲校学生总数为1 500,乙校学生总数为1 000,下列结论错误的是( )
A.甲校女生比乙校女生多
B.乙校男生比甲校男生少
C.乙校女生比甲校男生少
D.甲校女生比乙校男生少
4.为了解学生在“弘扬传统文化,品读经典文学”月的阅读情况,现从全校学生中随机抽取了部分学生,并统计了他们的阅读时间(阅读时间t∈[0,50]),分组整理数据得到如图所示的频率分布直方图.则图中a的值为( )
A.0.028 B.0.029
C.0.280 D.0.290
5.某射击运动员6次的训练成绩分别为:80,82,89,90,91,86,则这6次成绩的第80百分位数为( )
A.89 B.89.5
C.90 D.91
6.某校1 000名学生的高中历史学业水平考试成绩的频率直方图如图所示,规定90分及以上为优秀等级,则该校学生优秀等级的人数为( )
A.15 B.30
C.150 D.300
7.有一个容量为100的样本,数据分组及各组的频数如下:[12,15),5;[15,18),17;[18,21),17;[21,24),23;[24,27),19;[27,30),11;[30,33],8.则样本数据落在[21,30)内的频率为________.
8.河北省九大高峰按照海拔(单位:米)排名依次为小五台山(2 882)、驼梁山(2 281)、雾灵山(2 118)、长城岭(2 100)、白石山(2 096)、野三坡(1 983)、祖山(1 428)、天桂山(1 270)、狼牙山(1 105),则这九大高峰的海拔数据的第70百分位数为________.
关键能力综合练
1.为了了解某外贸企业职工对“一带一路”的认知程度,随机抽取了110名职工组织了“一带一路”知识竞赛.满分为100分(80分及以上为认知程度较高).并将所得成绩分组得到了如图所示的频率分布折线图.从频率分布折线图中得到的这110名职工成绩的信息正确的是( )
A.成绩是100分的人数比成绩是50分的人数多
B.对“一带一路”认知程度较高的人数是35
C.成绩是75分的人数为40
D.成绩落在[70,80)内的人数为20
2.某居民小区户主人数和户主对户型结构的满意率如图(1)和图(2)所示,为了解该小区户主对户型结构的满意程度,用比例分配的分层随机抽样方法抽取25%的户主作为样本进行调查,则样本容量和抽取的户主对四居室满意的人数分别为( )
A.200,16 B.200,18
C.240,16 D.240,18
3.某班同学进行社会实践,对年龄(单位:岁)在[25,55]内的人群随机抽取几人进行了生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率直方图,则下表中p,a的值分别为( )
组数 分组 低碳族的人数 占本组的频率
第一组 [25,30) 120 0.6
第二组 [30,35) 195 p
第三组 [35,40) 100 0.5
第四组 [40,45) a 0.4
第五组 [45,50) 30 0.3
第六组 [50,55] 15 0.3
A.0.79,20 B.0.195,40
C.0.65,60 D.0.975,80
4.为了鼓励学生积极锻炼身体,强健体魄,某学校决定每学期对体育成绩在年级前100名的学生给予专项奖励.已知该校高三年级共有500名学生,如图是该年级学生本学期体育测试成绩的频率分布直方图.据此估计,能够获得该项奖励的高三学生的最低分数为( )
A.89 B.88
C.87 D.86
5.(多选)新中国成立以来,我国一共进行了七次全国人口普查(以下简称“普查”),历次普查得到的全国人口总数如图1所示,城镇人口比重如图2所示.下列结论正确的是( )
A.第三次普查城镇人口数量低于2亿
B.对比这七次普查的结果,我国城镇人口数量逐次递增
C.第六次普查城镇人口数量超过第二次人口普查总人口数
D.与前一次普查对比,第五次普查的总人口增长量高于第四次普查的总人口增长量
6.(多选)所谓“民以食为天”,粮食问题就是人类生存的底线问题,是国家经济发展的底线问题,是社会维持稳定的底线问题.2021年,我国粮食总产量13 657亿斤,连续7年保持在1.3万亿斤以上,我国2020~2021年粮食产量种类分布及占比统计图如图所示,则下列说法正确的是( )
A.2021年的粮食总产量比2020年的粮食总产量高
B.2021年的稻谷产量比2020年的稻谷产量低
C.2020年和2021年的薯类所占比例保持稳定
D.2021年的各类粮食产量中,增长量最大的是小麦
7.某人对自己退休前后的工资分配做了详细的规划,各类费用的占比如下面的条形图和扇形图所示:
若他退休前每月工资为9 600元,退休后每月储蓄的金额比退休前每月储蓄的金额少1 680元,则他退休后每月工资为________元.
8.为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图如图.由于不慎将部分数据丢失,但知道前4组的频数的比为1∶3∶9∶27,后6组的频数递减5,设最大频率为a,则a的值为________,视力在4.6到5.0之间的学生数为b,则b的值为________.
9.某网红餐饮店因特色餐饮文化吸引了很多顾客“打卡”.现随机抽取了200桌就餐的顾客,统计其等待就餐的时间(等待时间不超过40分钟),将统计数据按[5,10),[10,15),…,[35,40]分组,制成如图所示的频率分布直方图.
(1)将所给的频率分布直方图补充完整;
(2)为进一步提升人气,该店给在等待时间从长到短的前20%的顾客中每桌赠送一份本店特色菜肴,试估计等待超过多长时间有赠品?
10.为了解某市家庭用电量的情况,该市统计局调查了100户居民去年一年的月均用电量,发现他们的用电量都在50 kW·h至350 kW·h之间,进行适当分组后,画出频率分布直方图如图所示.
(1)求a的值;
(2)求被调查用户中,用电量大于200 kW·h的户数;
(3)为了既满足居民的基本用电需求,又提高能源的利用效率,市政府计划采用阶梯定价,希望使85%的居民缴费在第一档(费用最低),请给出第一档用电标准(单位:kW·h)的建议,并简要说明理由.
核心素养升级练
1.郑州市某家保险公司的保险产品有以下五种:甲,一年期短险;乙,两全保险;丙,理财类保险;丁,定期寿险;戊,重大疾病保险.各种保险按相关约定进行参保与理赔,该保险公司对五个险种的参保客户进行抽样调查,得到如图所示的统计图,则以下四个说法中正确的是( )
A.42~53周岁客户人数是不低于54周岁的客户人数的4倍多
B.不低于54周岁客户参保总费用最多
C.丁险种人均参保费用最低
D.戊险种参保人都是42~53周岁的客户
2.某市教育局为了解疫情时期网络教学期间的学生学习情况,从该市随机抽取了1 000名高中学生,对他们每天的平均学习时间进行问卷调查,根据所得信息制作了如图所示的频率分布直方图,根据此图,估计该市高中学生每天的平均学习时间的60%分位数为________小时.
3.某大学艺术专业400名学生参加某次测评,根据男女学生人数比例、使用分层随机抽样的方法从中随机抽取了100名学生,记录他们的分数、将数据分成7组:[20,30),[30,40),…,[80,90],并整理得到如图的频率分布直方图.
(1)估计总体400名学生中分数小于60的人数;
(2)已知样本中分数小于40的学生有5人,试估计总体中分数在区间[40,50)内的人数;
(3)根据该大学规定,把25%的学生划定为不及格,确定本次测试的及格分数线,低于及格分数线的学生需要补考.
9.2.1 总体取值规律的估计
9.2.2 总体百分位数的估计
必备知识基础练
1.答案:C
解析:根据每种统计图的概念可知,折线图能有效地表示出每天的股价波动情况和趋势,我们能比较直观地看出此股票在这10天中,其价格总体趋势,也可以看出每天的变化,
∴用折线图表示不断变化的数据,是有优越性的.
故选C.
2.答案:D
解析:根据统计图可得惊蛰、小满、立秋的白昼时长大于11小时,
大寒节气的白昼时长低于11小时.
故选D.
3.答案:D
解析:甲校男生和女生的人数均为750,乙校男生人数为400,女生人数为600.
所以甲校女生比乙校女生多,故A正确;乙校男生比甲校男生少,故B正确;乙校女生比甲校男生少,故C正确;甲校女生比乙校男生多,故D错误.
故选D.
4.答案:A
解析:由(0.006+a+0.040+0.020+0.006)×10=1得a=0.028.
故选A.
5.答案:C
解析:该运动员6次的训练成绩从小到大排列为:80,82,86,89,90,91.
由6×80%=4.8,可得第80百分位数为从小到大排列的数据中的第5个数据,即90.
故选C.
6.答案:C
解析:根据频率直方图得该校学生优秀等级的概率是0.015×10=0.15,
故该校学生优秀等级的人数是1 000×0.15=150.
故选C.
7.答案:0.53
解析:依题意,样本数据落在[21,30)内的数据个数为:23+19+11=53,
所以样本数据落在[21,30)内的频率为=0.53.
8.答案:2 118
解析:将这九大高峰的海拔数据按照从小到大的顺序排列,依次为1 105,1 270,1 428,1 983,2 096,2 100,2 118,2 281,2 882,因为70%×9=6.3,所以第70百分位数为第7项数据,即2 118.
关键能力综合练
1.答案:C
解析:对于A,由于频率分布折线图表示的是某一个范围的频率,所以从频率分布折线图看不出成绩是100分的人数比成绩是50分的人数多,所以A错误;对于B,成绩为80分及以上的职工人数为×10×110=40,所以B错误;对于C,由题意可得成绩是75分的人数为110××10=40,故C正确;
对于D,成绩落在[70,80)内的人数为×10×110=40,D错误.
故选C.
2.答案:A
解析:由图(1)得该小区户主总人数为240+400+160=800(人),
所以样本容量为800×25%=200(人),
其中四居室户主有160×25%=40(人),
由图(2)得抽取的户主中对四居室满意的有40×40%=16(人).
故选A.
3.答案:C
解析:第一组人数为120÷0.6=200,第三组人数为100÷0.5=200,第五组人数为30÷0.3=100,第六组人数为15÷0.3=50,
由题中的频率直方图可得第一组频率为5×0.04=0.2,所以n==1 000,
所以第四组人数为5×0.03×1 000=150,所以a=150×0.4=60,
第二组人数为1 000-(200+200+150+100+50)=300,所以p==0.65.
故选C.
4.答案:B
解析:由题意,=0.2,[90,95)的频率为0.02×5=0.1,[85,90)的频率为0.05×5=0.25,则0.1<0.2<0.25,则第100名在[85,90)中,设分数为x,[x,90)的频率为0.2-0.1=0.1,所以=== x=88.
故选B.
5.答案:BD
解析:A:第三次普查城镇人口数量100 818×20.91%=21 081.043 8万人,即大于2亿,错误;B:各次普查总人口数逐年递增,同时城镇人口比重也逐年递增,故我国城镇人口数量逐次递增,正确;C:第六次普查城镇人口数量133 972×49.86%=66 798.439 2万人,而第二次人口普查总人口数为69 458万人,第六次普查城镇人口数量未超过第二次人口普查总人口数,错误;D:第五次普查的总人口增长量126 583-113 368=13 215万人,第四次普查的总人口增长量113 368-100 818=12 550万人,正确.
故选BD.
6.答案:AC
解析:2020年的粮食总产量为4 237+5 213+2 685+200+458+597=13 390亿斤,2021年的粮食总产量为4 257+5 451+2 739+208+393+609=13 657亿斤,因为13 657>13 390,故A正确;因为4 257>4 237,所以2021年的稻谷产量比2020年的稻谷产量高,故B错误;2020年和2021年的薯类所占比例都为4.46%,故C正确;
由统计图可得2021年的各类粮食产量中,增长量最大的是玉米,故D错误.
故选AC.
7.答案:8 000
解析:退休前每月储蓄的金额为9 600×0.30=2 880元,
退休后每月储蓄的金额为2 880-1 680=1 200元,
退休后每月工资为1 200÷0.15=8 000元.
8.答案:0.27 78
解析:设第1组的频数为x,则前4组的频数分别为x,3x,9x,27x,后5组的频数为27x-5,27x-10,27x-15,27x-20,27x-25,由题意得x+3x+9x+27x+(27x-5)+…+27x-25=100,即175x-75=100,解得x=1,
故a=0.27,b=78.
9.解析:(1)因为1-(0.036×5+0.04×5+0.048×5+0.04×5+0.012×5+0.008×5)=0.08,又0.08÷5=0.016,
所以频率分布直方图补充完整为
(2)设估计等待x分钟以上的顾客可以获得赠品,
由题意,0.008×5+0.012×5+(30-x)×0.04=0.2,解得x=27.5,
所以估计等待27分钟以上的顾客可以获得赠品.
10.解析:(1)因为(0.002 4+0.003 6+a+0.004 4+0.002 4+0.001 2)×50=1,所以a=0.006.
(2)根据频率分布直方图可知:“用电量大于200 kW·h”的频率为(0.004 4+0.002 4+0.001 2)×50=0.4,
所以用电量大于200 kW·h的户数为:100×0.4=40,
故用电量大于200 kW·h有40户;
(3)因为前四组的频率和为:(0.002 4+0.003 6+0.006+0.004 4)×50=0.82<0.85,
前五组的频率之和为(0.002 4+0.003 6+0.006+0.004 4+0.002 4)×50=0.94>0.85,
所以频率为0.85时对应的数据在第五组,
所以第一档用电标准为250+=262.5 kW·h.
故第一档用电标准为262.5 kW·h.
核心素养升级练
1.答案:A
解析:对观察参保人年龄分布的扇形图,42~53周岁客户人数占比33%,不低于54周岁的客户人数占比8%,42~53周岁客户人数是不低于54周岁的客户人数的4倍多,故A正确;统计图显示的是人均参保费用,由于人数未知,故不能确定哪个年龄段参保总费用最多,故B错误;由参保险种比例,丁险种参保比例最高,但统计图看不出丁险种的人均参保费用,故C错误;戊险种的参保人占比33%,42~53周岁客户人数占比33%,但统计图看不出两者相同,故D错误.
故选A.
2.答案:9.2
解析:由频率分布直方图可知,高中学生每天的平均学习时间的60%分位数在第3组,设其为x小时,则
0.05×2+0.10×2+0.25(x-8)=0.6,
解得x=9.2,
所以该市高中学生每天的平均学习时间的60%分位数约为9.2小时.
3.解析:(1)据频率分布直方图可知,样本中分数不小于60的频率为(0.02+0.04+0.02)×10=0.8,所以样本中分数小于60的频率为1-0.8=0.2,
所以估计总体400名学生中分数小于60的人数为400×0.2=80.
(2)根据题意,样本中分数不小于50的频率为(0.01+0.02+0.04+0.02)×10=0.9,
分数在区间[40,50)内的人数为100-100×0.9-5=5,
所以总体中分数在区间[40,50)内的人数估计为400×=20.
(3)设分数的第25百分位数为x,
分数小于70的频率为1-(0.04+0.02)×10=0.4,
分数小于60的频率为1-(0.02+0.04+0.02)×10=0.2,
所以x∈[60,70),即0.2+(x-60)×0.02=0.25,解得x=62.5,
则本次考试的及格分数线为62.5分.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
