沪科版数学七年级下册10.1相交线 同步练习(含答案)
文档属性
| 名称 | 沪科版数学七年级下册10.1相交线 同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 726.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-12 18:09:53 | ||
图片预览




文档简介
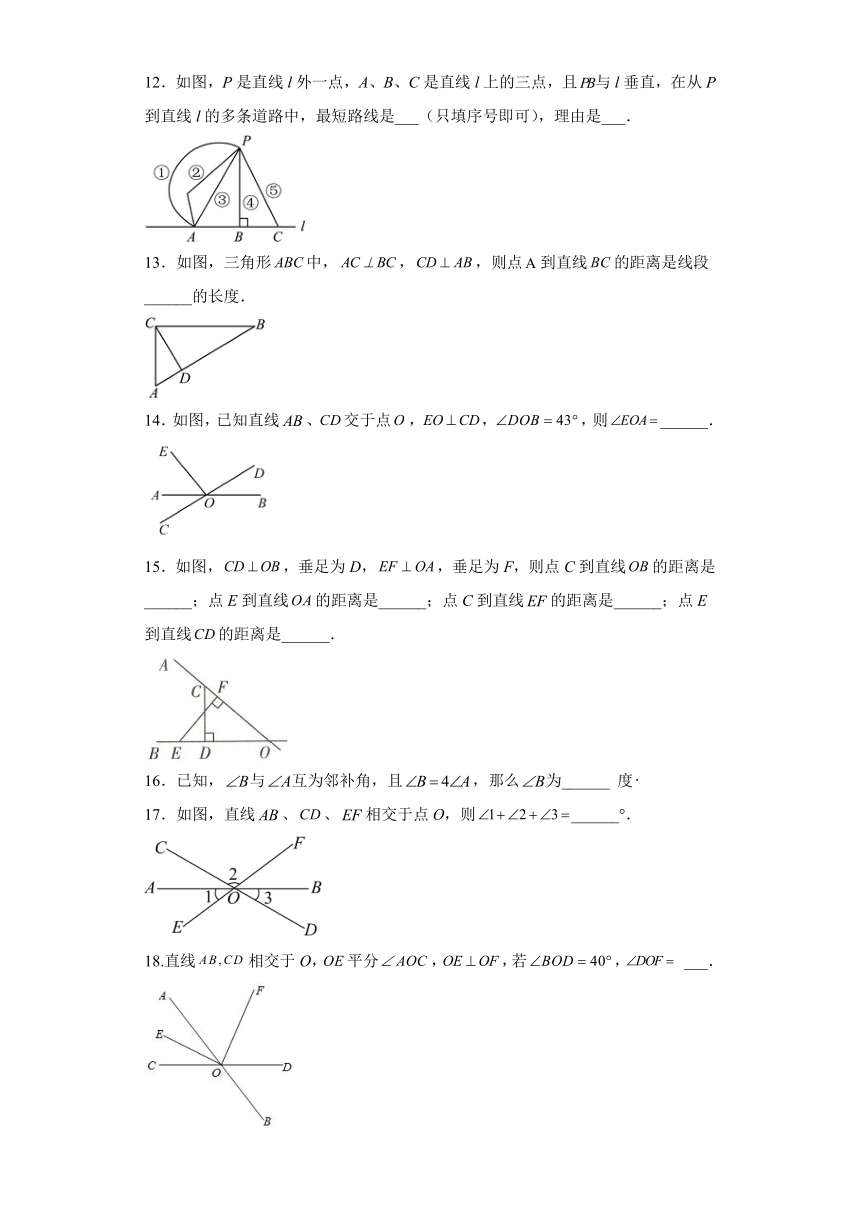
10.1 相交线 同步练习
一、单选题
1.下图与是对顶角的是( )
A. B. C. D.
2.如图,有三个快递员都从位于点P的快递站取到快递后,同时以相同的速度把取到的快递分别送到位于笔直公路l旁的三个快递点A、B、C、结果送到B快递点的快递员先到.理由是( )
A.垂线段最短 B.两点之间线段最短
C.两点确定一条直线 D.经过一点有无数条直线
3.如图,直线相交,若,图中与相等的角有( )
A.1个 B.2个 C.3个 D.4个
4.如图,,垂足为点O,直线经过点O.若,则度数为( )
A. B. C. D.
5.下列图形中,线段的长表示点到直线距离的是( )
A. B.
C. D.
6.如图,若以为端点在河上搭建一座桥,则搭建距离最短的是( )
A. B. C. D.
7.下列说法中错误的是( )
A.两条直线相交,所得的四个角中有一个角是,这两条直线一定互相垂直
B.两条直线的交点叫垂足
C.直线,也可以说成直线
D.直线外一点与直线上各点连接的所有线段中,垂线段最短
8.若点到直线距离为,点到直线距离为,则线段的长度为( )
A. B. C.或 D.至少
9.一个角的两边与另一个角的两边互相垂直,且这两个角之差为,那么这两个角分别为( )
A.和 B.和 C.和 D.和
10.如图,,,垂足为,则下列结论中,正确的个数为( )
①与互相垂直;②与互相垂直;③点到的垂线段是线段;④点到的距离是线段的长度;⑤点到的距离是线段的长度.
A. B. C. D.
二、填空题
11.如图,点P到一条笔直的公路共有四条路径,若要用相同速度从点P走到公路,最快到达的路径是选择沿线段去公路,这一选择用到的数学知识是______
12.如图,P是直线l外一点,A、B、C是直线l上的三点,且与l垂直,在从P到直线l的多条道路中,最短路线是___(只填序号即可),理由是___.
13.如图,三角形中,,,则点到直线的距离是线段______的长度.
14.如图,已知直线、交于点,,,则______.
15.如图,,垂足为D,,垂足为F,则点C到直线的距离是______;点E到直线的距离是______;点C到直线的距离是______;点E到直线的距离是______.
16.已知,与互为邻补角,且,那么为______ 度
17.如图,直线、、相交于点O,则______°.
18.直线相交于O,平分,,若, ___.
三、解答题
19.按下列语句画出图形:
(1)直线l经过A、B、C三点,点C在点A与点B之间;
(2)P是直线a外一点,经过点P有一条直线b与直线a相交于点Q;
(3)P是内一点,过点P作射线的垂线,垂足为E.
20.给下面命题的说理过程填写依据.
已知:如图,O是直线上的一点,是的平分线,是的平分线.对说明理由.
理由:因为(__________________),
(__________________),
所以
(__________________).
所以(两角和的定义).
所以(__________________).
21.如图,直线,,相交于点.
(1)写出,的邻补角;
(2)写出,的对顶角;
(3)如果,求,.
22.如图,将一块直角三角板的直角顶点O放在直线上.
(1)若线段的长是点C到直线的距离,则点D在直线______(填“上”或“外”).
(2)比较与的大小,并说明理由.
23.如图,直线相交于点O,平分,.
(1)若,求的度数;
(2)若,猜想与之间的位置关系,并证明.
24.如图,直线,相交于点,.
(1)若,,则_______;
(2)若,判断与的位置关系,并说明理由;
(3)若,求和的度数.
参考答案:
1.A
2.A
3.C
4.C
5.D
6.A
7.B
8.D
9.A
10.B
11.垂线段最短
12. 垂线段最短
13.
14.
15. 线段的长 线段的长 线段的长 线段的长
16.
17.180
18./70度
19.【详解】(1)解:如图所示:
;
(2)解:如图所示:
;
(3)解:如图所示:
.
20.【详解】理由:因为(角平分线的定义),
(角平分线的定义),
所以
(等量代换).
所以(两角和的定义).
所以(垂直的定义).
21.【详解】(1)解:由图及题意可知:的邻补角是,;
的邻补角是:,;
(2)的对顶角是,的对顶角是;
(3)∵,
∴,
∴,
∴;.
22.【详解】(1)解:∵线段的长是点C到直线的距离,
∴,
∵,
∴,重合,
∴则点D在直线上.
(2),理由如下:
∵,
∴与上各点的连线段中,垂线段最短.
∴.
23【详解】(1)解:∵(已知),
(邻补角互补),
∴,
∵ 平分(已知),
∴ (角平分线的定义),
∴ (对顶角相等),
(2),理由如下:
∵,,
∴,
∵ (邻补角互补),
∴,
∵ 平分(已知),
∴ (角平分线的定义),
∴,
∴(垂直的定义).
24.【详解】(1)解:∵,
∴,
∵,
∴,
∵
∴;
(2)解:.
理由:
∵,
∴,
即,
∵,
∴,
即,
∴;
(3)解:∵,
∴,
又,
∴,
∴,
由(1)知:,
∴,
∴,
∴.
一、单选题
1.下图与是对顶角的是( )
A. B. C. D.
2.如图,有三个快递员都从位于点P的快递站取到快递后,同时以相同的速度把取到的快递分别送到位于笔直公路l旁的三个快递点A、B、C、结果送到B快递点的快递员先到.理由是( )
A.垂线段最短 B.两点之间线段最短
C.两点确定一条直线 D.经过一点有无数条直线
3.如图,直线相交,若,图中与相等的角有( )
A.1个 B.2个 C.3个 D.4个
4.如图,,垂足为点O,直线经过点O.若,则度数为( )
A. B. C. D.
5.下列图形中,线段的长表示点到直线距离的是( )
A. B.
C. D.
6.如图,若以为端点在河上搭建一座桥,则搭建距离最短的是( )
A. B. C. D.
7.下列说法中错误的是( )
A.两条直线相交,所得的四个角中有一个角是,这两条直线一定互相垂直
B.两条直线的交点叫垂足
C.直线,也可以说成直线
D.直线外一点与直线上各点连接的所有线段中,垂线段最短
8.若点到直线距离为,点到直线距离为,则线段的长度为( )
A. B. C.或 D.至少
9.一个角的两边与另一个角的两边互相垂直,且这两个角之差为,那么这两个角分别为( )
A.和 B.和 C.和 D.和
10.如图,,,垂足为,则下列结论中,正确的个数为( )
①与互相垂直;②与互相垂直;③点到的垂线段是线段;④点到的距离是线段的长度;⑤点到的距离是线段的长度.
A. B. C. D.
二、填空题
11.如图,点P到一条笔直的公路共有四条路径,若要用相同速度从点P走到公路,最快到达的路径是选择沿线段去公路,这一选择用到的数学知识是______
12.如图,P是直线l外一点,A、B、C是直线l上的三点,且与l垂直,在从P到直线l的多条道路中,最短路线是___(只填序号即可),理由是___.
13.如图,三角形中,,,则点到直线的距离是线段______的长度.
14.如图,已知直线、交于点,,,则______.
15.如图,,垂足为D,,垂足为F,则点C到直线的距离是______;点E到直线的距离是______;点C到直线的距离是______;点E到直线的距离是______.
16.已知,与互为邻补角,且,那么为______ 度
17.如图,直线、、相交于点O,则______°.
18.直线相交于O,平分,,若, ___.
三、解答题
19.按下列语句画出图形:
(1)直线l经过A、B、C三点,点C在点A与点B之间;
(2)P是直线a外一点,经过点P有一条直线b与直线a相交于点Q;
(3)P是内一点,过点P作射线的垂线,垂足为E.
20.给下面命题的说理过程填写依据.
已知:如图,O是直线上的一点,是的平分线,是的平分线.对说明理由.
理由:因为(__________________),
(__________________),
所以
(__________________).
所以(两角和的定义).
所以(__________________).
21.如图,直线,,相交于点.
(1)写出,的邻补角;
(2)写出,的对顶角;
(3)如果,求,.
22.如图,将一块直角三角板的直角顶点O放在直线上.
(1)若线段的长是点C到直线的距离,则点D在直线______(填“上”或“外”).
(2)比较与的大小,并说明理由.
23.如图,直线相交于点O,平分,.
(1)若,求的度数;
(2)若,猜想与之间的位置关系,并证明.
24.如图,直线,相交于点,.
(1)若,,则_______;
(2)若,判断与的位置关系,并说明理由;
(3)若,求和的度数.
参考答案:
1.A
2.A
3.C
4.C
5.D
6.A
7.B
8.D
9.A
10.B
11.垂线段最短
12. 垂线段最短
13.
14.
15. 线段的长 线段的长 线段的长 线段的长
16.
17.180
18./70度
19.【详解】(1)解:如图所示:
;
(2)解:如图所示:
;
(3)解:如图所示:
.
20.【详解】理由:因为(角平分线的定义),
(角平分线的定义),
所以
(等量代换).
所以(两角和的定义).
所以(垂直的定义).
21.【详解】(1)解:由图及题意可知:的邻补角是,;
的邻补角是:,;
(2)的对顶角是,的对顶角是;
(3)∵,
∴,
∴,
∴;.
22.【详解】(1)解:∵线段的长是点C到直线的距离,
∴,
∵,
∴,重合,
∴则点D在直线上.
(2),理由如下:
∵,
∴与上各点的连线段中,垂线段最短.
∴.
23【详解】(1)解:∵(已知),
(邻补角互补),
∴,
∵ 平分(已知),
∴ (角平分线的定义),
∴ (对顶角相等),
(2),理由如下:
∵,,
∴,
∵ (邻补角互补),
∴,
∵ 平分(已知),
∴ (角平分线的定义),
∴,
∴(垂直的定义).
24.【详解】(1)解:∵,
∴,
∵,
∴,
∵
∴;
(2)解:.
理由:
∵,
∴,
即,
∵,
∴,
即,
∴;
(3)解:∵,
∴,
又,
∴,
∴,
由(1)知:,
∴,
∴,
∴.
