人教版数学七年级下册7.2.2 用坐标表示平移 说课课件(共22张PPT)
文档属性
| 名称 | 人教版数学七年级下册7.2.2 用坐标表示平移 说课课件(共22张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-12 18:46:48 | ||
图片预览







文档简介
(共22张PPT)
4
1
2
3
5
1
本节课是在学移的概念和性质的基础上,进一步用坐标刻画平移变换。本节课的学习对之后的平面图形平移变换,及函数图像平移变换的学习有着非常重要的引导作用。
教材的地位与作用
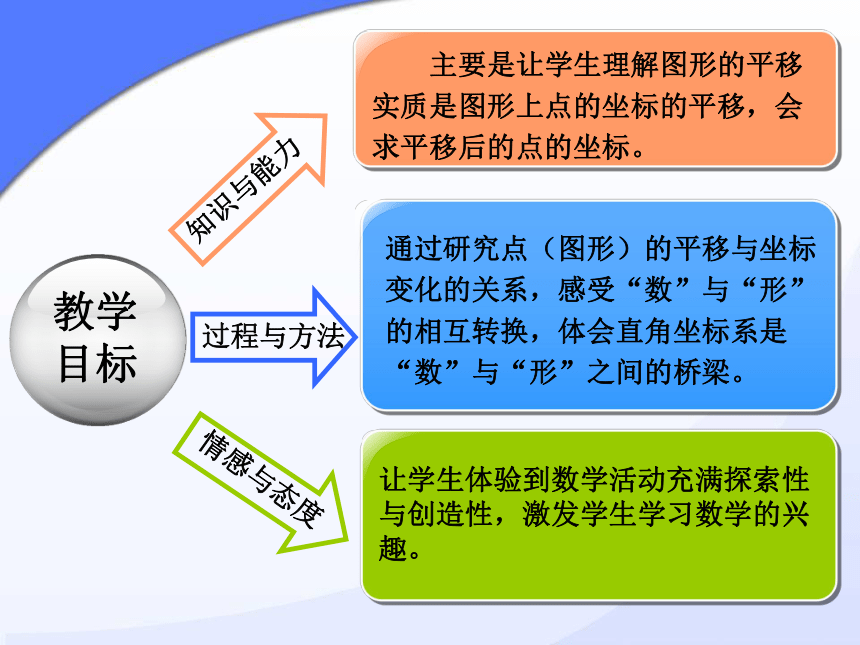
教学目标
知识与能力
过程与方法
主要是让学生理解图形的平移实质是图形上点的坐标的平移,会求平移后的点的坐标。
通过研究点(图形)的平移与坐标变化的关系,感受“数”与“形”的相互转换,体会直角坐标系是“数”与“形”之间的桥梁。
让学生体验到数学活动充满探索性与创造性,激发学生学习数学的兴趣。
情感与态度
掌握坐标变化与图形平移的关系。
利用坐标变化与图形平移的关系解决实际问题。
教学重点
教学难点
4
1
2
3
5
2
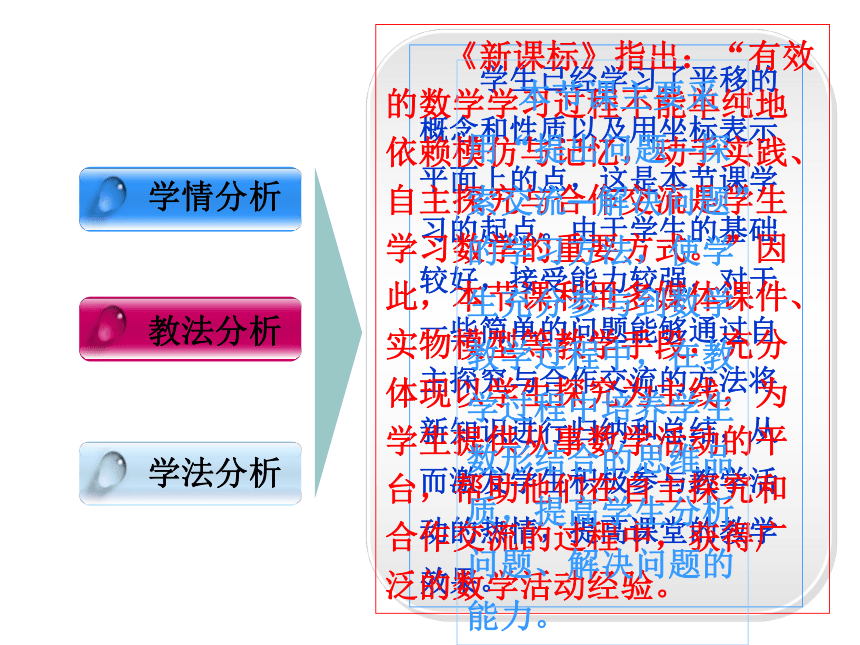
学情分析
教法分析
学法分析
学生已经学移的概念和性质以及用坐标表示平面上的点,这是本节课学习的起点。由于学生的基础较好,接受能力较强,对于一些简单的问题能够通过自主探究与合作交流的方法将新知识进行归纳和总结,从而激发学生积极参与教学活动的热情,提高课堂的教学效果。
《新课标》指出:“有效的数学学习过程不能单纯地依赖模仿与记忆,动手实践、自主探究与合作交流是学生学习数学的重要方式。”因此,本节课利用多媒体课件、实物模型等教学手段,充分体现以学生探究为主线,为学生提供从事数学活动的平台,帮助他们在自主探究和合作交流的过程中,获得广泛的数学活动经验。
本节课主要采用“提出问题—探索交流—解决问题”的学习方法,使学生充分参与到数学教学过程中,在教学过程中培养学生数形结合的思维品质,提高学生分析问题、解决问题的能力。
4
1
2
3
5
3
(一)创设情境
引入新知
在中国象棋的棋盘中建立一个平面直角坐标系,红炮原来的位置为(0,0)点。
(1)将红炮向右或向左移动一定的单位长度,则红炮现在在什么地方?
设计意图:
中国象棋的棋盘学生非常熟悉,学生利用真实棋盘进行动手实践,让学生经历数学知识的形成与应用过程,发现坐标系中点的平移与坐标变化的关系。
(2)将红炮向上或向下移动一定的单位长度,则红炮现在又在什么地方?
(3)先将红炮在左右方向上平移,再在上下方向上平移一定的单位长度,红炮会到达什么位置?
A1.
A.
A2.
A1.
A2.
(二)合作交流
形成新知
设计意图:
通过刚才的动手实践,鼓励学生自主探究与合作交流。此时学生已经对图形上点的平移与坐标变化的关系有了初步的认识。通过几道简单的练习题,让学生巩固所学新知,熟练运用所得规律解题。
图形上点的坐标变化 与图形平移间的关系
总结规律1:
向左平移a个单位
向右平移a个单位
(x-a,y)
(x,y)
(x,y+b)
(x,y-b)
向上
平移
b个
单位
向下
平移
b个
单位
(x+a,y)
已知点P(5,-3)。
1.把点P向右平移3个单位长度后得到的P1点的坐标是
2.把点P向下平移4个单位长度后得到的P2点的坐标是
3.把点P向左平移6个单位长度后得到的P3点的坐标是
4.把点P向上平移3个单位长度后得到的P4点的坐标是
(三)设置问题
突出重点
设计意图:学生已经能够熟练运用点的平移与坐标变化的关系解题,此时给出一个图形中某个点的坐标变化,让学生通过实验,得到坐标变化与图形平移的关系。
△ABC三个顶点坐标如图所示:
(1)将三角形ABC三个点的横坐标都减去6,纵坐标不变得到A1,B1,C1三点;将三角形ABC三个点的纵坐标都减去5,横坐标不变得到A2,B2,C2三点。
(2)将三角形ABC三个点的横坐标都减去6,纵坐标减去4得到A3,B3,C3三点。
-5 -4 -3 -2 -1 0 1 2 3 4 x
3
2
1
-2
-1
-3
4
y
A
B
C
A1
B1
C1
(4,3)
(1,2)
(3,1)
A2
B2
C2
A3
B3
C3
(四)综合应用
巩固新知
设计意图:
通过前面的学习,学生已经掌握图形经过一次平移后坐标的变化规律,此时设计一道二次平移的练习题,目的在于让学生能够将所学知识总结提高。
(1)把鱼向右或向左平移几个单位,再向上或向下平移几个单位,你能说出顶点的坐标是多少吗?
(2)如果鱼的顶点坐标发生了变化,你能看出鱼是如何平移的吗?
x
y
O
由形到数
由数到形
设计意图:
设计一道逆向思维的题目,即已知平移后点的坐标以及平移方向和距离,求平移前点的坐标,目的在于培养学生逆向思维的能力。
问题:将点P先向右平移3个单位,再向下平移5个单位,得到
点P’(2,-2),则平移前点P的坐标是多少
(五) 拓展应用、提升能力
平移前点的坐标
右3,下5
平移后点的坐标
(2,-2)
(x-3,y+5)
(-1,3)
方法一:
方法二:
(x,y)
(2,-2)
(x+3,y-5)
x+3=2,y-5=-2
左3,上5
(六) 归纳小结、发展深化
谈一谈:今天你有什么收获?
设计意图:本环节由学生自己总结学习的收获。目的是培养学生的归纳总结能力,锻炼他们的语言表达能力。
(七)分层作业、巩固提高
布置作业:
1、教科书 习题7.2 第3、4、6题
2、将一个三角形的三个顶点的坐标分别向上平移2个单位长度,再向左平移3个单位长度所得点的坐标分别是(2,1),(-1,3),(4,-5),则平移前三个顶点的坐标分别是多少?
设计意图:
尊重学生的个体差异,满足多样化的学习需要,因此习题难易设置不同,目的是让每个学生的思维都能得到最大潜力的挖掘。
4
1
2
3
5
向上
平移
b个
单位
向下
平移
b个
单位
向左平移a个单位
向右平移a个单位
(x-a,y)
(x,y)
(x,y+b)
(x,y-b)
(x+a,y)
平移前
点的坐标
平移方向
和距离
平移后
点的坐标
7.2.2 用坐标表示平移
图形上点的坐标变化与图形平移间的关系:
设计意图:目的是突出重点,给学生一个清晰的知识轮廓。
4
1
2
3
5
设计说明
①创设轻松愉快的学习氛围,让学生在快乐中获取新知,在探索中掌握新知。
②从学生感兴趣的实际问题出发,引入新课,激发学生学习的积极性,使学生能够积极参与。
③设计不同的题型,由易到难,循序渐进,符合学生的认知规律,从而达到掌握新知的目的。
④我认为,作为一名数学老师,教学要面向全体学生,对于学生之间存在的个体差异,在练习题的布置上应注重难易结合,对各个层次学生的潜能进行最大限度的开发。
4
1
2
3
5
1
本节课是在学移的概念和性质的基础上,进一步用坐标刻画平移变换。本节课的学习对之后的平面图形平移变换,及函数图像平移变换的学习有着非常重要的引导作用。
教材的地位与作用
教学目标
知识与能力
过程与方法
主要是让学生理解图形的平移实质是图形上点的坐标的平移,会求平移后的点的坐标。
通过研究点(图形)的平移与坐标变化的关系,感受“数”与“形”的相互转换,体会直角坐标系是“数”与“形”之间的桥梁。
让学生体验到数学活动充满探索性与创造性,激发学生学习数学的兴趣。
情感与态度
掌握坐标变化与图形平移的关系。
利用坐标变化与图形平移的关系解决实际问题。
教学重点
教学难点
4
1
2
3
5
2
学情分析
教法分析
学法分析
学生已经学移的概念和性质以及用坐标表示平面上的点,这是本节课学习的起点。由于学生的基础较好,接受能力较强,对于一些简单的问题能够通过自主探究与合作交流的方法将新知识进行归纳和总结,从而激发学生积极参与教学活动的热情,提高课堂的教学效果。
《新课标》指出:“有效的数学学习过程不能单纯地依赖模仿与记忆,动手实践、自主探究与合作交流是学生学习数学的重要方式。”因此,本节课利用多媒体课件、实物模型等教学手段,充分体现以学生探究为主线,为学生提供从事数学活动的平台,帮助他们在自主探究和合作交流的过程中,获得广泛的数学活动经验。
本节课主要采用“提出问题—探索交流—解决问题”的学习方法,使学生充分参与到数学教学过程中,在教学过程中培养学生数形结合的思维品质,提高学生分析问题、解决问题的能力。
4
1
2
3
5
3
(一)创设情境
引入新知
在中国象棋的棋盘中建立一个平面直角坐标系,红炮原来的位置为(0,0)点。
(1)将红炮向右或向左移动一定的单位长度,则红炮现在在什么地方?
设计意图:
中国象棋的棋盘学生非常熟悉,学生利用真实棋盘进行动手实践,让学生经历数学知识的形成与应用过程,发现坐标系中点的平移与坐标变化的关系。
(2)将红炮向上或向下移动一定的单位长度,则红炮现在又在什么地方?
(3)先将红炮在左右方向上平移,再在上下方向上平移一定的单位长度,红炮会到达什么位置?
A1.
A.
A2.
A1.
A2.
(二)合作交流
形成新知
设计意图:
通过刚才的动手实践,鼓励学生自主探究与合作交流。此时学生已经对图形上点的平移与坐标变化的关系有了初步的认识。通过几道简单的练习题,让学生巩固所学新知,熟练运用所得规律解题。
图形上点的坐标变化 与图形平移间的关系
总结规律1:
向左平移a个单位
向右平移a个单位
(x-a,y)
(x,y)
(x,y+b)
(x,y-b)
向上
平移
b个
单位
向下
平移
b个
单位
(x+a,y)
已知点P(5,-3)。
1.把点P向右平移3个单位长度后得到的P1点的坐标是
2.把点P向下平移4个单位长度后得到的P2点的坐标是
3.把点P向左平移6个单位长度后得到的P3点的坐标是
4.把点P向上平移3个单位长度后得到的P4点的坐标是
(三)设置问题
突出重点
设计意图:学生已经能够熟练运用点的平移与坐标变化的关系解题,此时给出一个图形中某个点的坐标变化,让学生通过实验,得到坐标变化与图形平移的关系。
△ABC三个顶点坐标如图所示:
(1)将三角形ABC三个点的横坐标都减去6,纵坐标不变得到A1,B1,C1三点;将三角形ABC三个点的纵坐标都减去5,横坐标不变得到A2,B2,C2三点。
(2)将三角形ABC三个点的横坐标都减去6,纵坐标减去4得到A3,B3,C3三点。
-5 -4 -3 -2 -1 0 1 2 3 4 x
3
2
1
-2
-1
-3
4
y
A
B
C
A1
B1
C1
(4,3)
(1,2)
(3,1)
A2
B2
C2
A3
B3
C3
(四)综合应用
巩固新知
设计意图:
通过前面的学习,学生已经掌握图形经过一次平移后坐标的变化规律,此时设计一道二次平移的练习题,目的在于让学生能够将所学知识总结提高。
(1)把鱼向右或向左平移几个单位,再向上或向下平移几个单位,你能说出顶点的坐标是多少吗?
(2)如果鱼的顶点坐标发生了变化,你能看出鱼是如何平移的吗?
x
y
O
由形到数
由数到形
设计意图:
设计一道逆向思维的题目,即已知平移后点的坐标以及平移方向和距离,求平移前点的坐标,目的在于培养学生逆向思维的能力。
问题:将点P先向右平移3个单位,再向下平移5个单位,得到
点P’(2,-2),则平移前点P的坐标是多少
(五) 拓展应用、提升能力
平移前点的坐标
右3,下5
平移后点的坐标
(2,-2)
(x-3,y+5)
(-1,3)
方法一:
方法二:
(x,y)
(2,-2)
(x+3,y-5)
x+3=2,y-5=-2
左3,上5
(六) 归纳小结、发展深化
谈一谈:今天你有什么收获?
设计意图:本环节由学生自己总结学习的收获。目的是培养学生的归纳总结能力,锻炼他们的语言表达能力。
(七)分层作业、巩固提高
布置作业:
1、教科书 习题7.2 第3、4、6题
2、将一个三角形的三个顶点的坐标分别向上平移2个单位长度,再向左平移3个单位长度所得点的坐标分别是(2,1),(-1,3),(4,-5),则平移前三个顶点的坐标分别是多少?
设计意图:
尊重学生的个体差异,满足多样化的学习需要,因此习题难易设置不同,目的是让每个学生的思维都能得到最大潜力的挖掘。
4
1
2
3
5
向上
平移
b个
单位
向下
平移
b个
单位
向左平移a个单位
向右平移a个单位
(x-a,y)
(x,y)
(x,y+b)
(x,y-b)
(x+a,y)
平移前
点的坐标
平移方向
和距离
平移后
点的坐标
7.2.2 用坐标表示平移
图形上点的坐标变化与图形平移间的关系:
设计意图:目的是突出重点,给学生一个清晰的知识轮廓。
4
1
2
3
5
设计说明
①创设轻松愉快的学习氛围,让学生在快乐中获取新知,在探索中掌握新知。
②从学生感兴趣的实际问题出发,引入新课,激发学生学习的积极性,使学生能够积极参与。
③设计不同的题型,由易到难,循序渐进,符合学生的认知规律,从而达到掌握新知的目的。
④我认为,作为一名数学老师,教学要面向全体学生,对于学生之间存在的个体差异,在练习题的布置上应注重难易结合,对各个层次学生的潜能进行最大限度的开发。
