北师大版 数学七年级上册 5.2求解一元一次方程 第1课时 教案
文档属性
| 名称 | 北师大版 数学七年级上册 5.2求解一元一次方程 第1课时 教案 |  | |
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-12 19:30:59 | ||
图片预览

文档简介
第五章一元一次方程
5.2 求解一元一次方程
第1课时
一、教学目标
1.进一步熟悉利用等式的基本性质解一元一次方程的基本技能.
2.在解方程的过程中分析、归纳出移项法则,并能运用这一法则解方程.
3.体会学习移项法则解一元一次方程必要性,使学生在动手、独立思考的过程中,进一步体会方程模型的作用,体会学习数学的实用性.
二、教学重点及难点
重点:理解移项法则,会解简单的一元一次方程
难点:用移项法则解方程,注意移项要变号.
三、教学准备
多媒体课件
四、相关资源
微课《利用“移项”解一元一次方程》,知识卡片《解一元一次方程(一)--移项》
五、教学过程
【复习回顾】复习回顾,引入新课
1.利用等式的性质解下列方程
(1)x-2=8;
(2)3x=2x+1.
解:(1)利用等式的性质1,两边都加上2得:x-2+2=8+2.即x=10.
(2)利用等式的性质1,两边都减去2x得:3x-2x=2x+1-2x.即x=10.
2.比较原方程3x=2x+1与变形后的方程3x-2x=1,你又发现了什么?
解:通过变形,可以简化方程,使含未知数的项与常数项分别位于方程左右两边,使方程更接近于x=a的形式.
设计意图:本节直接用复习上节所学重点知识的方式导入新课,一是可以反馈学生对知识点的落实情况,二是其中的等式基本性质1就是新课中移项法则的理论依据,有一举两得的功效.
【新知讲解】合作交流,探求新知
探究:移项的定义及法则
活动1.阅读解方程的过程:
解:(1)5x-2=8,方程两边都加上2,得5x-2+2=8+2,
即5x=10,
即x=2.
(2)7x=6x-4,方程两边都减去6x,得7x-6x=6x-6x-4,
即7x-6x=-4,
即x=-4.
活动2.观察归纳,解答问题
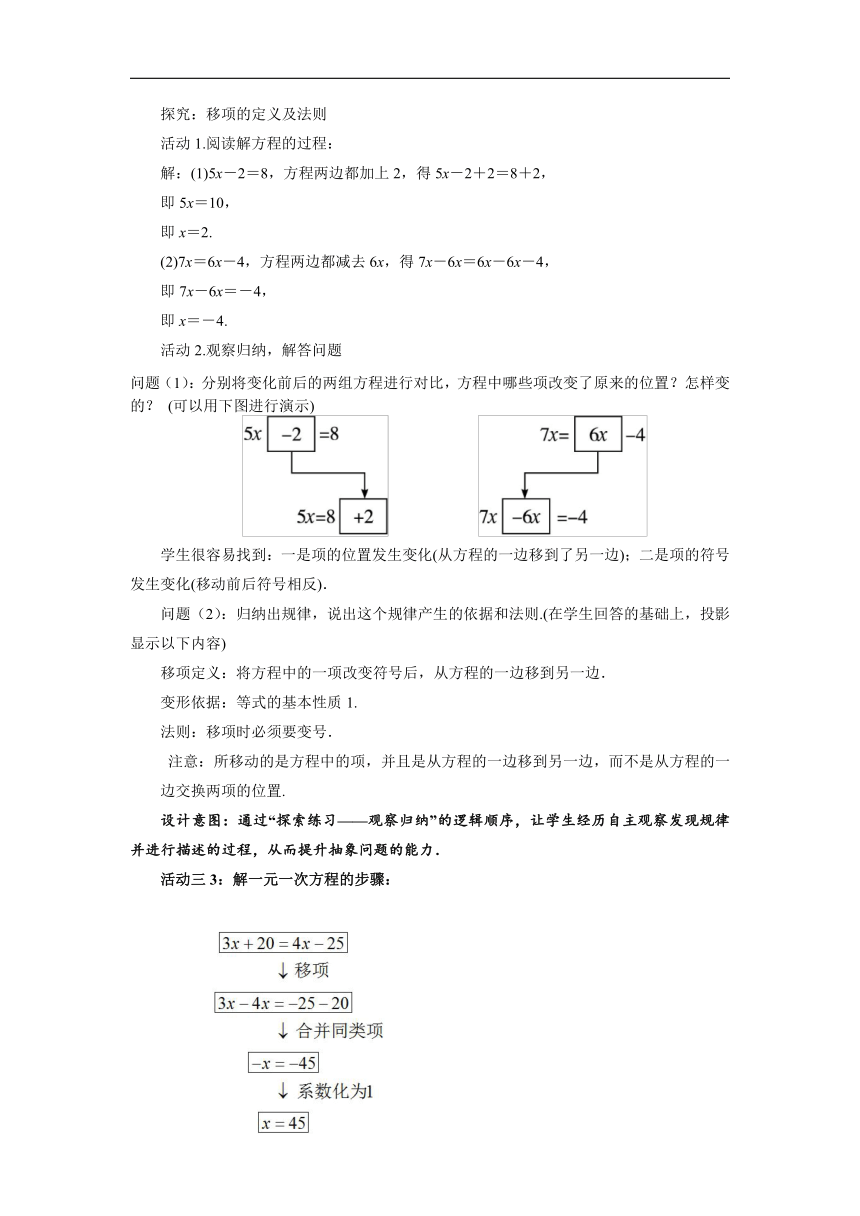
问题(1):分别将变化前后的两组方程进行对比,方程中哪些项改变了原来的位置?怎样变的? (可以用下图进行演示)
学生很容易找到:一是项的位置发生变化(从方程的一边移到了另一边);二是项的符号发生变化(移动前后符号相反).
问题(2):归纳出规律,说出这个规律产生的依据和法则.(在学生回答的基础上,投影显示以下内容)
移项定义:将方程中的一项改变符号后,从方程的一边移到另一边.
变形依据:等式的基本性质1.
法则:移项时必须要变号.
注意:所移动的是方程中的项,并且是从方程的一边移到另一边,而不是从方程的一边交换两项的位置.
设计意图:通过“探索练习——观察归纳”的逻辑顺序,让学生经历自主观察发现规律并进行描述的过程,从而提升抽象问题的能力.
活动三3:解一元一次方程的步骤:
设计意图:教师通过书写解方程的过程,可以提高学生解题的规范性.而采用框图表示解方程的过程,是为使解法中各步骤的先后顺序清晰,渗透算法程序的思想.教学中不要求学生也画框图.
【典型例题】
例1.解下列方程:
(1)3x+3=2x+7;(2)2x+6=1.
解:(1)移项,得3x-2x=7-3.
合并同类项,得x=4.
(2)移项,得2x=1-6.
合并同类项,得2x=-5.
方程两边同除以2,得x=-.
例2.判断下列移项是否正确,正确的在题后的括号里打“√”,错误的打“×”.
(1)从得到; ( × )
(2)从得到. ( √ )
例3.下列方程的变形是移项的是( D ).
(A)由得 (B)由得
(C)由得 (D)由得
本题可以采用学生口述,教师板演的方法,因为这是解方程一节安排的第一组例题,教学时必须强调解题的规范步骤和格式,同时教师还应及时纠正学生可能出现的错误,适时组织学生交流改错.
例4.解方程:x=-x+3.
解:移项,得x+x=3.
合并同类项,得x=3.
方程两边同除以(或同乘以),得x=4.
本题建议首先放手让学生去做.学生可能采取多种方法解答,教学时不应拘泥于教材提供的解法,只要合理都应该给予鼓励.
设计意图:进一步巩固利用移项、合并同类项解方程的方法.
【随堂练习】
1.把下列方程进行移项变换
2x-5=12移项2x=12+
7x=-x+2移项7x+ =2
4x=-x+10移项4x+ =10
8x-5=3x+1移项8x+ =1+
-x+3=-9x+7移项-x+ =7+
2.解方程:
(1)3x+5=4x+1;(2)9-3y=5y+5.
解: (1)移项,得:3x-4x=1-5.
合并同类项,得:-x=-4.
系数化为1,得:x=4.
(2)移项,得:-3y-5y=5-9.
合并同类项,得:-8y=-4.
系数化为1,得:y=.
(3)
移项,得
合并同类项,得:
系数化为1,得:x=1.
(4)移项,得
合并同类项,得:
系数化为1,得:.
3.下列移项对不对?如果不对,错在哪里?应当怎样改正?
(1)从3x+6=0得3x=6;
(2)从2x=x-1得到2x-x=1;
(3)从2+x-3=2x+1得到2-3-1=2x-x;
解:(1)不对,移项要变号;应该得:3x=-6;
(2)不对,不移项的部分不用变号;应该得:2x-x=-1;
(3)对.
4.根据下列条件列出方程,然后求出某数:
(1)某数的等于32;
(2)某数的2倍比某数的5倍小24.
解:(1)设某数为x,则.解得x=288.
(2)设某数为x,则5x-2x=24.解得x=8.
设计意图:通过练习,及时巩固新知识,加深对化归思想的理解.
六、课堂小结
1.谈谈你对解方程的认识.
2.谈谈你本节课还有什么收获.
设计意图:教师引导学生归纳本节课的知识要点和思想方法,使学生对列方程和解方程有一个整体全面的认识,同时也帮助学生养成良好的学习习惯.
七、板书设计
2.求解一元一次方程
一、移项:
移项要变号
二、练习.
5.2 求解一元一次方程
第1课时
一、教学目标
1.进一步熟悉利用等式的基本性质解一元一次方程的基本技能.
2.在解方程的过程中分析、归纳出移项法则,并能运用这一法则解方程.
3.体会学习移项法则解一元一次方程必要性,使学生在动手、独立思考的过程中,进一步体会方程模型的作用,体会学习数学的实用性.
二、教学重点及难点
重点:理解移项法则,会解简单的一元一次方程
难点:用移项法则解方程,注意移项要变号.
三、教学准备
多媒体课件
四、相关资源
微课《利用“移项”解一元一次方程》,知识卡片《解一元一次方程(一)--移项》
五、教学过程
【复习回顾】复习回顾,引入新课
1.利用等式的性质解下列方程
(1)x-2=8;
(2)3x=2x+1.
解:(1)利用等式的性质1,两边都加上2得:x-2+2=8+2.即x=10.
(2)利用等式的性质1,两边都减去2x得:3x-2x=2x+1-2x.即x=10.
2.比较原方程3x=2x+1与变形后的方程3x-2x=1,你又发现了什么?
解:通过变形,可以简化方程,使含未知数的项与常数项分别位于方程左右两边,使方程更接近于x=a的形式.
设计意图:本节直接用复习上节所学重点知识的方式导入新课,一是可以反馈学生对知识点的落实情况,二是其中的等式基本性质1就是新课中移项法则的理论依据,有一举两得的功效.
【新知讲解】合作交流,探求新知
探究:移项的定义及法则
活动1.阅读解方程的过程:
解:(1)5x-2=8,方程两边都加上2,得5x-2+2=8+2,
即5x=10,
即x=2.
(2)7x=6x-4,方程两边都减去6x,得7x-6x=6x-6x-4,
即7x-6x=-4,
即x=-4.
活动2.观察归纳,解答问题
问题(1):分别将变化前后的两组方程进行对比,方程中哪些项改变了原来的位置?怎样变的? (可以用下图进行演示)
学生很容易找到:一是项的位置发生变化(从方程的一边移到了另一边);二是项的符号发生变化(移动前后符号相反).
问题(2):归纳出规律,说出这个规律产生的依据和法则.(在学生回答的基础上,投影显示以下内容)
移项定义:将方程中的一项改变符号后,从方程的一边移到另一边.
变形依据:等式的基本性质1.
法则:移项时必须要变号.
注意:所移动的是方程中的项,并且是从方程的一边移到另一边,而不是从方程的一边交换两项的位置.
设计意图:通过“探索练习——观察归纳”的逻辑顺序,让学生经历自主观察发现规律并进行描述的过程,从而提升抽象问题的能力.
活动三3:解一元一次方程的步骤:
设计意图:教师通过书写解方程的过程,可以提高学生解题的规范性.而采用框图表示解方程的过程,是为使解法中各步骤的先后顺序清晰,渗透算法程序的思想.教学中不要求学生也画框图.
【典型例题】
例1.解下列方程:
(1)3x+3=2x+7;(2)2x+6=1.
解:(1)移项,得3x-2x=7-3.
合并同类项,得x=4.
(2)移项,得2x=1-6.
合并同类项,得2x=-5.
方程两边同除以2,得x=-.
例2.判断下列移项是否正确,正确的在题后的括号里打“√”,错误的打“×”.
(1)从得到; ( × )
(2)从得到. ( √ )
例3.下列方程的变形是移项的是( D ).
(A)由得 (B)由得
(C)由得 (D)由得
本题可以采用学生口述,教师板演的方法,因为这是解方程一节安排的第一组例题,教学时必须强调解题的规范步骤和格式,同时教师还应及时纠正学生可能出现的错误,适时组织学生交流改错.
例4.解方程:x=-x+3.
解:移项,得x+x=3.
合并同类项,得x=3.
方程两边同除以(或同乘以),得x=4.
本题建议首先放手让学生去做.学生可能采取多种方法解答,教学时不应拘泥于教材提供的解法,只要合理都应该给予鼓励.
设计意图:进一步巩固利用移项、合并同类项解方程的方法.
【随堂练习】
1.把下列方程进行移项变换
2x-5=12移项2x=12+
7x=-x+2移项7x+ =2
4x=-x+10移项4x+ =10
8x-5=3x+1移项8x+ =1+
-x+3=-9x+7移项-x+ =7+
2.解方程:
(1)3x+5=4x+1;(2)9-3y=5y+5.
解: (1)移项,得:3x-4x=1-5.
合并同类项,得:-x=-4.
系数化为1,得:x=4.
(2)移项,得:-3y-5y=5-9.
合并同类项,得:-8y=-4.
系数化为1,得:y=.
(3)
移项,得
合并同类项,得:
系数化为1,得:x=1.
(4)移项,得
合并同类项,得:
系数化为1,得:.
3.下列移项对不对?如果不对,错在哪里?应当怎样改正?
(1)从3x+6=0得3x=6;
(2)从2x=x-1得到2x-x=1;
(3)从2+x-3=2x+1得到2-3-1=2x-x;
解:(1)不对,移项要变号;应该得:3x=-6;
(2)不对,不移项的部分不用变号;应该得:2x-x=-1;
(3)对.
4.根据下列条件列出方程,然后求出某数:
(1)某数的等于32;
(2)某数的2倍比某数的5倍小24.
解:(1)设某数为x,则.解得x=288.
(2)设某数为x,则5x-2x=24.解得x=8.
设计意图:通过练习,及时巩固新知识,加深对化归思想的理解.
六、课堂小结
1.谈谈你对解方程的认识.
2.谈谈你本节课还有什么收获.
设计意图:教师引导学生归纳本节课的知识要点和思想方法,使学生对列方程和解方程有一个整体全面的认识,同时也帮助学生养成良好的学习习惯.
七、板书设计
2.求解一元一次方程
一、移项:
移项要变号
二、练习.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
