课堂分层优化系列之基础提升练10.2直方图(一)(含解析)
文档属性
| 名称 | 课堂分层优化系列之基础提升练10.2直方图(一)(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-11 00:26:52 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
课堂分层优化系列之基础提升练10.2直方图(一)
一.选择题(共8小题,每小题4分,共32分)
1.如图是某组15名学生数学测试成绩的频数分布直方图,则成绩低于60分的人数是( )
A.3人 B.6人 C.10人 D.14人
2.列一组数据的频数分布表时,落在各个小组内的数据的个数叫做( )
A.组距 B.频数 C.频率 D.样本容量
3.下列5个实数、、π、、中,无理数出现的频数是( )
A.2 B.3 C.4 D.5
4.某校对1200名女生的身高进行了测量,身高在1.58m~1.63m这一小组的频率为0.25,则该组共有( )
A.400人 B.300人 C.200人 D.100人
5.某篮球队员在一次训练中共投篮80次,命中了其中的64次,该运动员在这次训练中投篮命中的频率为( )
A.0.64 B.0.8 C.1.25 D.64
6.给出下面一组数据:19,20,25,31,28,27,26,21,20,22,24,23,25,29,27,28,27,30,18,20.若组距为2,则这组数据应分成( )组.
A.4 B.5 C.6 D.7
7.一组数据的最大值是132,最小值是89,将这组数据进行分组时,取组距为5,则组数是( )
A.7 B.8 C.9 D.10
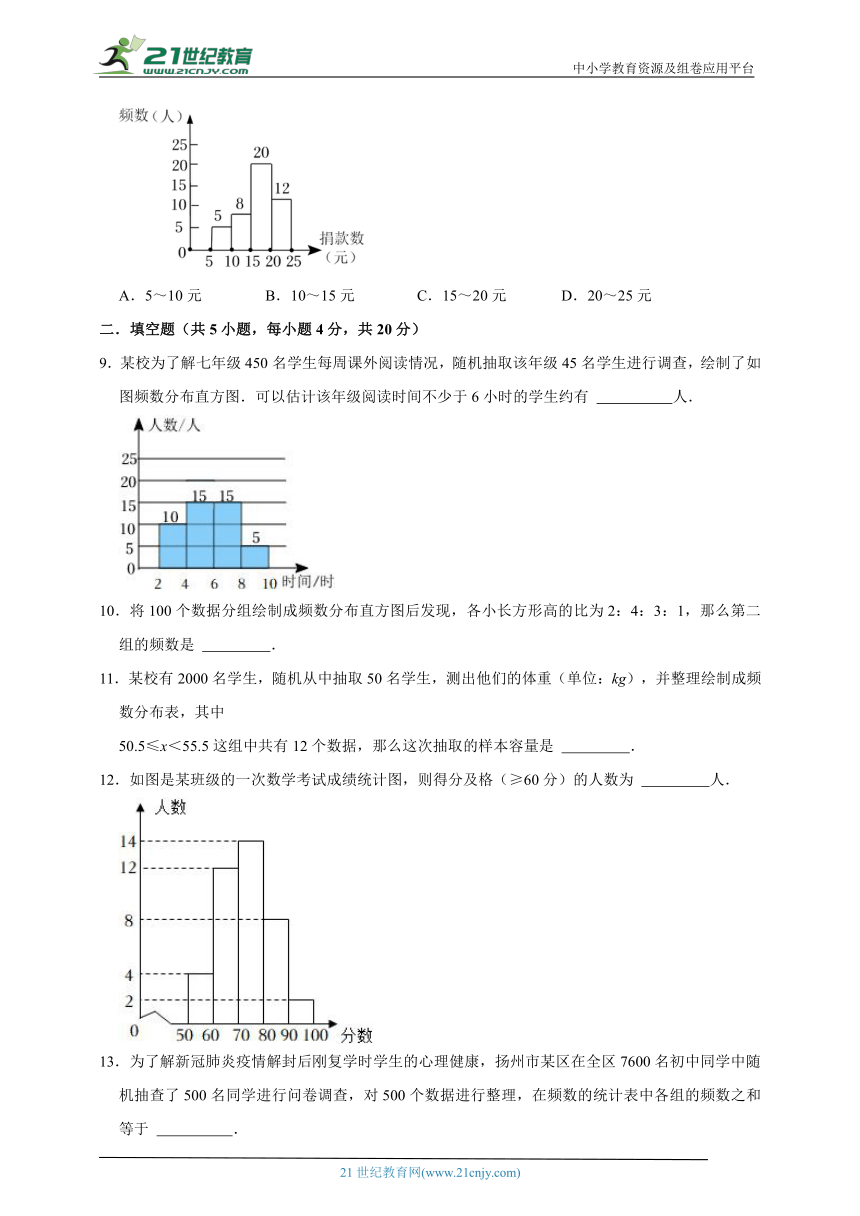
8.如图是某班45名同学爱心捐款额的频数分布直方图(每组含前一个边界值,不含后一个边界值),则捐款人数最少的一组是( )
A.5~10元 B.10~15元 C.15~20元 D.20~25元
二.填空题(共5小题,每小题4分,共20分)
9.某校为了解七年级450名学生每周课外阅读情况,随机抽取该年级45名学生进行调查,绘制了如图频数分布直方图.可以估计该年级阅读时间不少于6小时的学生约有 人.
10.将100个数据分组绘制成频数分布直方图后发现,各小长方形高的比为2:4:3:1,那么第二组的频数是 .
11.某校有2000名学生,随机从中抽取50名学生,测出他们的体重(单位:kg),并整理绘制成频数分布表,其中
50.5≤x<55.5这组中共有12个数据,那么这次抽取的样本容量是 .
12.如图是某班级的一次数学考试成绩统计图,则得分及格(≥60分)的人数为 人.
13.为了解新冠肺炎疫情解封后刚复学时学生的心理健康,扬州市某区在全区7600名初中同学中随机抽查了500名同学进行问卷调查,对500个数据进行整理,在频数的统计表中各组的频数之和等于 .
三.解答题(共6小题,每小题8分,共48分)
14.一只不透明的袋中装有红球和黄球,全班同学都按序在袋中任意摸出1只球再放回袋内(摸球之前要搅匀),最后发现同学们摸到红球的频率比黄球大.这可能是什么原因?
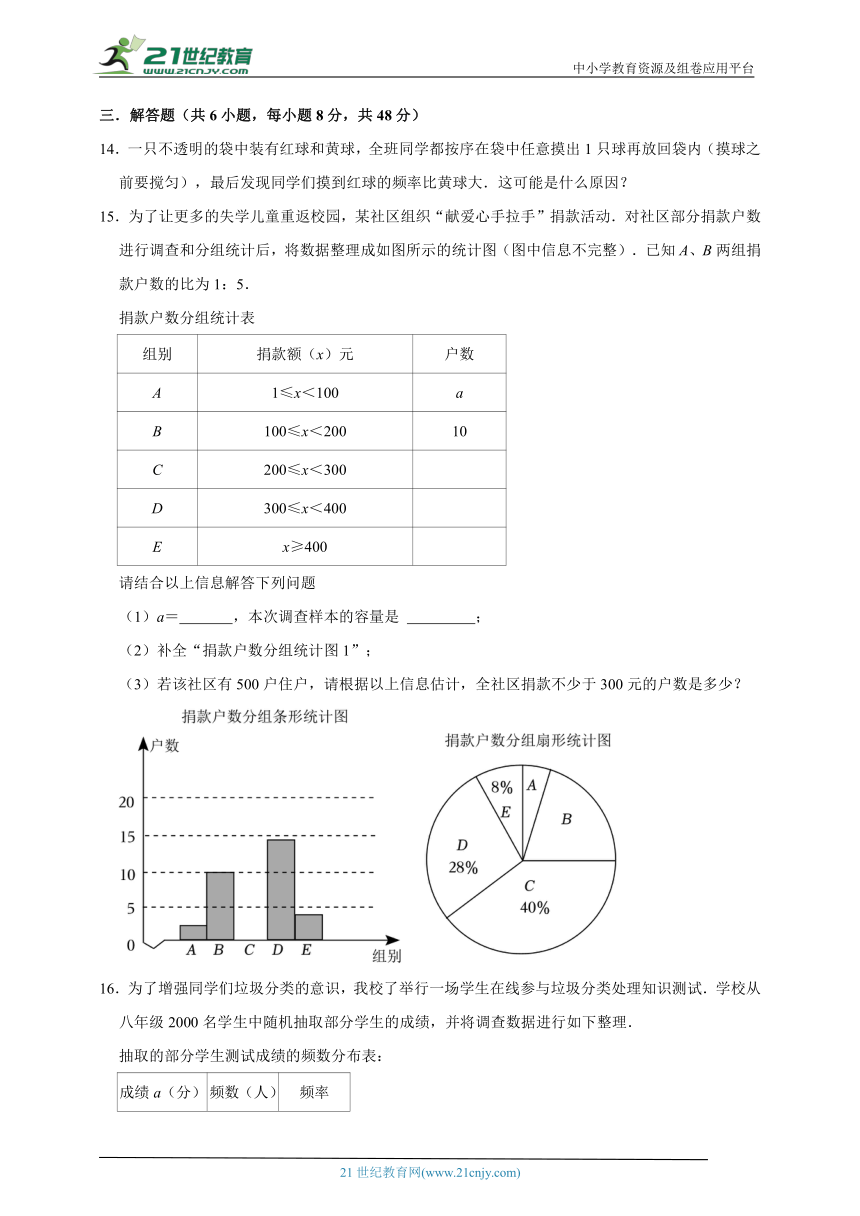
15.为了让更多的失学儿童重返校园,某社区组织“献爱心手拉手”捐款活动.对社区部分捐款户数进行调查和分组统计后,将数据整理成如图所示的统计图(图中信息不完整).已知A、B两组捐款户数的比为1:5.
捐款户数分组统计表
组别 捐款额(x)元 户数
A 1≤x<100 a
B 100≤x<200 10
C 200≤x<300
D 300≤x<400
E x≥400
请结合以上信息解答下列问题
(1)a= ,本次调查样本的容量是 ;
(2)补全“捐款户数分组统计图1”;
(3)若该社区有500户住户,请根据以上信息估计,全社区捐款不少于300元的户数是多少?
16.为了增强同学们垃圾分类的意识,我校了举行一场学生在线参与垃圾分类处理知识测试.学校从八年级2000名学生中随机抽取部分学生的成绩,并将调查数据进行如下整理.
抽取的部分学生测试成绩的频数分布表:
成绩a(分) 频数(人) 频率
50≤a<60 10 0.1
60≤a<70 15 n
70≤a<80 m 0.2
80≤a<90 40 0.4
90≤a<100 15 0.15
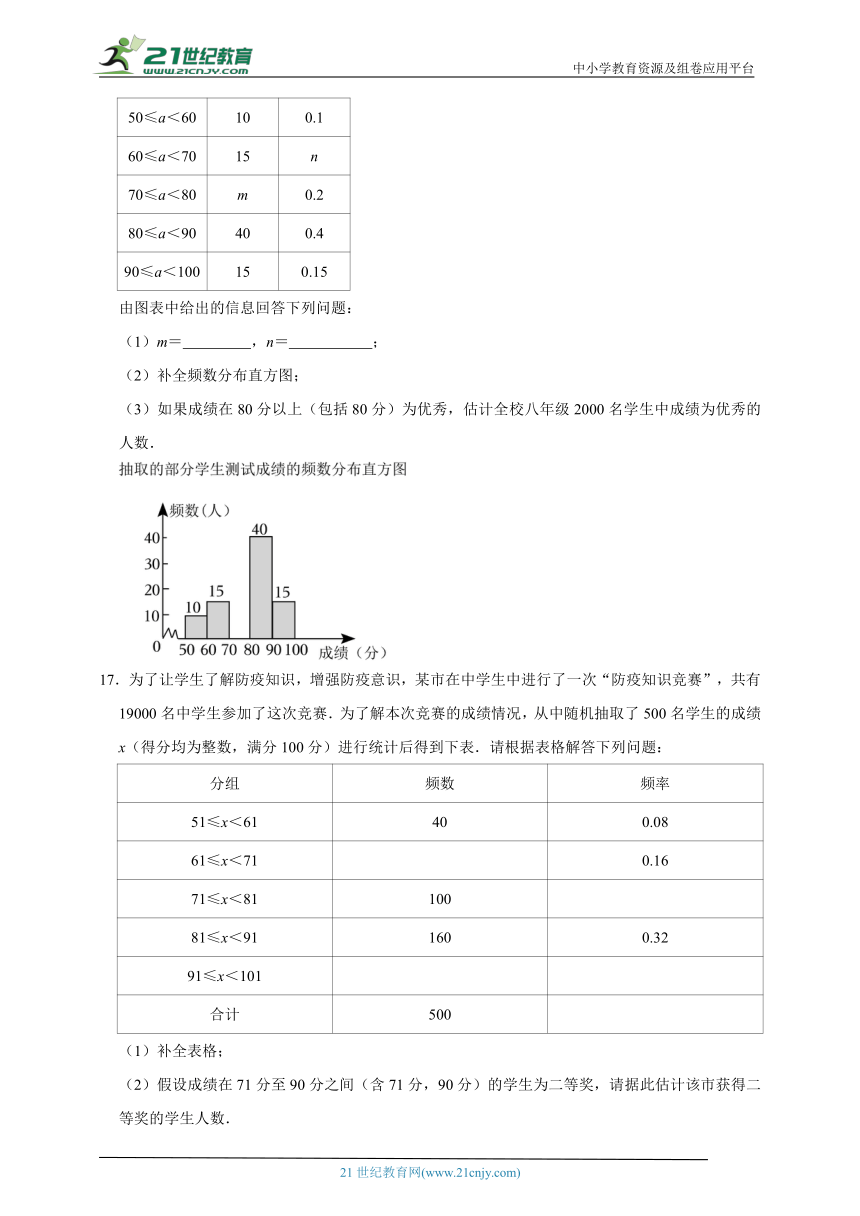
由图表中给出的信息回答下列问题:
(1)m= ,n= ;
(2)补全频数分布直方图;
(3)如果成绩在80分以上(包括80分)为优秀,估计全校八年级2000名学生中成绩为优秀的人数.
17.为了让学生了解防疫知识,增强防疫意识,某市在中学生中进行了一次“防疫知识竞赛”,共有19000名中学生参加了这次竞赛.为了解本次竞赛的成绩情况,从中随机抽取了500名学生的成绩x(得分均为整数,满分100分)进行统计后得到下表.请根据表格解答下列问题:
分组 频数 频率
51≤x<61 40 0.08
61≤x<71 0.16
71≤x<81 100
81≤x<91 160 0.32
91≤x<101
合计 500
(1)补全表格;
(2)假设成绩在71分至90分之间(含71分,90分)的学生为二等奖,请据此估计该市获得二等奖的学生人数.
18.从某服装厂即将出售的一批休闲装中抽检200件,其中不合格的休闲装有15件.
(1)抽检中合格的频数,频率分别是多少?
(2)销售3000套这样的休闲装,大约有多少件不合格的休闲装?
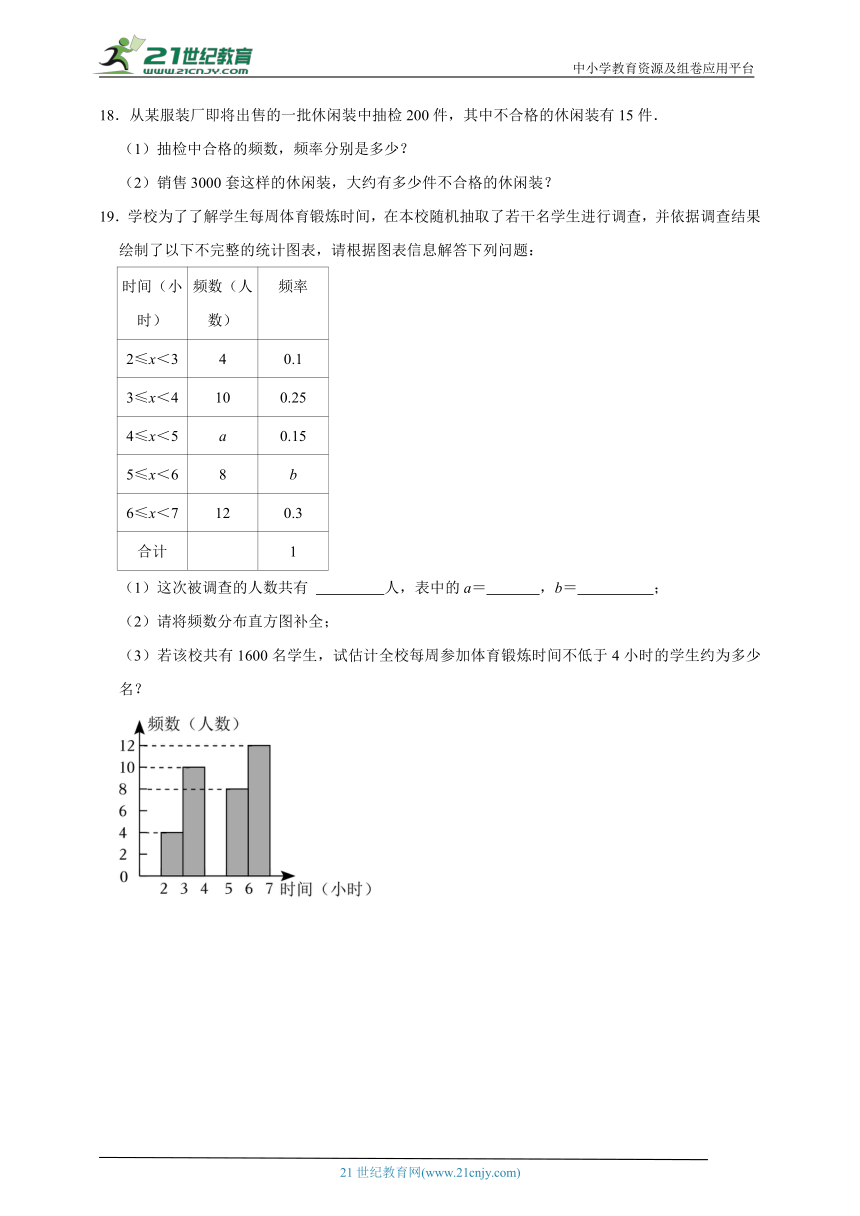
19.学校为了了解学生每周体育锻炼时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表,请根据图表信息解答下列问题:
时间(小时) 频数(人数) 频率
2≤x<3 4 0.1
3≤x<4 10 0.25
4≤x<5 a 0.15
5≤x<6 8 b
6≤x<7 12 0.3
合计 1
(1)这次被调查的人数共有 人,表中的a= ,b= ;
(2)请将频数分布直方图补全;
(3)若该校共有1600名学生,试估计全校每周参加体育锻炼时间不低于4小时的学生约为多少名?
课堂分层优化系列之基础提升练10.2直方图(一)
参考答案与试题解析
一.选择题(共8小题,每小题4分,共32分)
1.如图是某组15名学生数学测试成绩的频数分布直方图,则成绩低于60分的人数是( )
A.3人 B.6人 C.10人 D.14人
【分析】根据直方图中的数据,可以得到成绩低于60分的人数,本题得以解决.
【解答】解:由直方图可知,
成绩低于60分的人数是1+2=3,
故选:A.
【点评】本题考查频数分布直方图,解答本题的关键是明确题意,利用数形结合的思想解答.
2.列一组数据的频数分布表时,落在各个小组内的数据的个数叫做( )
A.组距 B.频数 C.频率 D.样本容量
【分析】根据频数的定义,即落在各个小组内的数据的个数,可知B是答案.
【解答】解:由于频数是指落在各个小组内的数据的个数,故选B.
【点评】本题考查频数的定义,即落在各个小组内的数据的个数.
3.下列5个实数、、π、、中,无理数出现的频数是( )
A.2 B.3 C.4 D.5
【分析】根据频数的定义解决问题即可.
【解答】解:在、、π、、中,无理数有:、、π,无理数出现的频数是3.
故选:B.
【点评】本题考查频数与频率,有理数,无理数等知识,解题的关键是理解频数的定义.
4.某校对1200名女生的身高进行了测量,身高在1.58m~1.63m这一小组的频率为0.25,则该组共有( )
A.400人 B.300人 C.200人 D.100人
【分析】根据频率=频数÷总数,得:频数=总数×频率,进而即可求解.
【解答】解:根据题意,该组的人数为1200×0.25=300(人).
故选:B.
【点评】本题考查了频率的计算公式,理解公式.频率等于频数除以总数,能够灵活运用是关键.
5.某篮球队员在一次训练中共投篮80次,命中了其中的64次,该运动员在这次训练中投篮命中的频率为( )
A.0.64 B.0.8 C.1.25 D.64
【分析】根据频率的公式:频率=即可直接求解.
【解答】解:该运动员在这次训练中投篮命中的频率为=0.8.
故选:B.
【点评】本题考查了频率的计算公式,理解公式是关键.
6.给出下面一组数据:19,20,25,31,28,27,26,21,20,22,24,23,25,29,27,28,27,30,18,20.若组距为2,则这组数据应分成( )组.
A.4 B.5 C.6 D.7
【分析】用极差除以组距,如果商是整数,组数=这个整数加1,如果商不是整数,用进一法,确定组数.
【解答】解:∵(31﹣18)÷2=6.5,
∴分成的组数是7组,
故选:D.
【点评】本题考查频数分布直方图、组距、极差,组数之间的关系等知识,掌握组数的定义是本题的关键,即数据分成的组的个数称为组数.
7.一组数据的最大值是132,最小值是89,将这组数据进行分组时,取组距为5,则组数是( )
A.7 B.8 C.9 D.10
【分析】根据组数=(最大值﹣最小值)÷组距进行计算即可,注意小数部分要进位.
【解答】解:∵数据的最大值是132,最小值是89,
∴极差为132﹣89=43,
又∵组距为5,
∴43÷5=8.6,
∴组数为9,
故选:C.
【点评】此题考查了列频数分布表时组数的计算,掌握组数的定义是本题的关键,即数据分成的组的个数称为组数.
8.如图是某班45名同学爱心捐款额的频数分布直方图(每组含前一个边界值,不含后一个边界值),则捐款人数最少的一组是( )
A.5~10元 B.10~15元 C.15~20元 D.20~25元
【分析】根据直方图中的数据可以解答本题.
【解答】解:由直方图可得,捐款人数最少的一组是5~10元,只有5个人,
故选:A.
【点评】本题考查频数分布直方图,解答本题的关键是明确题意,读懂频数分布直方图.
二.填空题(共5小题)
9.某校为了解七年级450名学生每周课外阅读情况,随机抽取该年级45名学生进行调查,绘制了如图频数分布直方图.可以估计该年级阅读时间不少于6小时的学生约有 200 人.
【分析】根据图表数据,利用总人数乘以阅读时间不少于6小时的学生所占的百分数即可求解.
【解答】解:由图可知阅读时间不少于6小时的学生为450×=200(人).
故答案为:200.
【点评】本题考查读频数分布直方图的能力和利用统计图获取信息的能力.
10.将100个数据分组绘制成频数分布直方图后发现,各小长方形高的比为2:4:3:1,那么第二组的频数是 40 .
【分析】频数分布直方图中,各个长方形的高之比依次为2:4:3:1,则指各组频数之比为2:4:3:1,据此即可求出第二小组的频数
【解答】解:∵频数分布直方图中各个长方形的高之比依次为2:4:3:1,样本容量为100,
∴第二小组的频数为100×=40.
故答案为:40.
【点评】此题考查了频数(率)分布直方图,要知道,频数分布直方图中各个长方形的高之比即为各组频数之比.
11.某校有2000名学生,随机从中抽取50名学生,测出他们的体重(单位:kg),并整理绘制成频数分布表,其中
50.5≤x<55.5这组中共有12个数据,那么这次抽取的样本容量是 50 .
【分析】根据样本容量的定义:一个样本包括的个体数量叫做样本容量,即可得出答案.
【解答】解:样本容量:一个样本包括的个体数量叫做样本容量.样本容量只是个数字,没有单位.
故答案为:50.
【点评】本题考查了样本容量的定义,正确理解定义的关键.
12.如图是某班级的一次数学考试成绩统计图,则得分及格(≥60分)的人数为 36 人.
【分析】根据频数分布直方图中的数据可以得出得分及格(≥60分)的人数.
【解答】解:得分及格(≥60分)的人数为12+14+8+2=36(人),
故答案为:36.
【点评】本题考查频数分布直方图,解答本题的关键是利用数形结合的思想解答.
13.为了解新冠肺炎疫情解封后刚复学时学生的心理健康,扬州市某区在全区7600名初中同学中随机抽查了500名同学进行问卷调查,对500个数据进行整理,在频数的统计表中各组的频数之和等于 500 .
【分析】根据各小组频数之和等于数据总和可求得结果.
【解答】解:为了解新冠肺炎疫情解封后刚复学时学生的心理健康,扬州市某区在全区7600名初中同学中随机抽查了500名同学进行问卷调查,对500个数据进行整理,在频数的统计表中各组的频数之和等于500.
故答案为:500.
【点评】本题是对频率与频数灵活运用的综合考查,各小组频数之和等于数据总和,而各小组频率之和为1.
三.解答题(共6小题)
14.一只不透明的袋中装有红球和黄球,全班同学都按序在袋中任意摸出1只球再放回袋内(摸球之前要搅匀),最后发现同学们摸到红球的频率比黄球大.这可能是什么原因?
【分析】根据球的个数和实验条件解答即可.
【解答】解:摸到红球的可能性比黄球大,说明这个袋中红球比黄球多.
【点评】本题考查了频率和频数以及可能性大小的比较:只要总情况数目相同,谁包含的情况数目多,谁的可能性就大;反之也成立;若包含的情况相当,那么它们的可能性就相等.注意实验条件不同得到的结论也不同.
15.为了让更多的失学儿童重返校园,某社区组织“献爱心手拉手”捐款活动.对社区部分捐款户数进行调查和分组统计后,将数据整理成如图所示的统计图(图中信息不完整).已知A、B两组捐款户数的比为1:5.
捐款户数分组统计表
组别 捐款额(x)元 户数
A 1≤x<100 a
B 100≤x<200 10
C 200≤x<300
D 300≤x<400
E x≥400
请结合以上信息解答下列问题
(1)a= 2 ,本次调查样本的容量是 50 ;
(2)补全“捐款户数分组统计图1”;
(3)若该社区有500户住户,请根据以上信息估计,全社区捐款不少于300元的户数是多少?
【分析】(1)根据B组的户数和所占的份数,计算每一份有2户,A组的频数是2,样本的容量=A、B两组捐款户数÷A、B两组捐款户数所占的百分比;
(2)C组的频数=样本的容量×C组所占的百分比;
(3)捐款不少于300元的有D、E两组,捐款不少于300元的户数=500×D、E两组捐款户数所占的百分比;
【解答】解:(1)A组的频数是:
(10÷5)×1=2;
调查样本的容量是:
(10+2)÷(1﹣40%﹣28%﹣8%)=50,
故答案为:2,50;
(2)C组的频数是:50×40%=20,如图.
(3)∵500×(28%+8%)=180,
∴全社区捐款不少于300元的户数是180户;
答:估计全社区捐款不少于300元的户数是180户.
【点评】本题考查读频数分布直方图的能力和利用统计图获取信息的能力.利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
16.为了增强同学们垃圾分类的意识,我校了举行一场学生在线参与垃圾分类处理知识测试.学校从八年级2000名学生中随机抽取部分学生的成绩,并将调查数据进行如下整理.
抽取的部分学生测试成绩的频数分布表:
成绩a(分) 频数(人) 频率
50≤a<60 10 0.1
60≤a<70 15 n
70≤a<80 m 0.2
80≤a<90 40 0.4
90≤a<100 15 0.15
由图表中给出的信息回答下列问题:
(1)m= 20 ,n= 0.15 ;
(2)补全频数分布直方图;
(3)如果成绩在80分以上(包括80分)为优秀,估计全校八年级2000名学生中成绩为优秀的人数.
【分析】(1)先求出样本容量,再根据频率=频数÷样本容量求解即可得出答案;
(2)根据所求m的值即可补全图形;
(3)总人数乘以成绩在80分以上(包括80分)的人数所占比例即可.
【解答】解:(1)∵样本容量为10÷0.1=100,
∴m=100×0.2=20,n=15÷100=0.15,
故答案为:20、0.15;
(2)补全直方图如下:
(3)2000×(0.4+0.15)=1100(人),
答:估计全校八年级2000名学生中成绩为优秀的人数约为1100人.
【点评】本题考查频数分布直方图、频数分布表,解答本题的关键是明确题意,利用数形结合的思想解答.
17.为了让学生了解防疫知识,增强防疫意识,某市在中学生中进行了一次“防疫知识竞赛”,共有19000名中学生参加了这次竞赛.为了解本次竞赛的成绩情况,从中随机抽取了500名学生的成绩x(得分均为整数,满分100分)进行统计后得到下表.请根据表格解答下列问题:
分组 频数 频率
51≤x<61 40 0.08
61≤x<71 0.16
71≤x<81 100
81≤x<91 160 0.32
91≤x<101
合计 500
(1)补全表格;
(2)假设成绩在71分至90分之间(含71分,90分)的学生为二等奖,请据此估计该市获得二等奖的学生人数.
【分析】(1)频率=频数÷总数、频数之和等于总数求解即可;
(2)用总人数乘以对应频率之和即可.
【解答】解(1)根据频率=频数÷总数得:500×0.16=80,100÷500=0.2,500﹣40﹣80﹣100﹣160=120,120÷500=0.24,
故表格如图所示:
分组 频数 频率
51≤x<61 40 0.08
61≤x<71 80 0.16
71≤x<81 100 0.2
81≤x<91 160 0.32
91≤x<101 120 0.24
合计 500 1
(2)故估计该市获得二等奖的学生人数为:19000×(0.2+0.32)=9880(人),
答:估计该市获得二等奖的学生人数为9880人.
【点评】本题主要考查频数(率)分布表,解题的关键是掌握频率=频数÷总数、频数之和等于总数.
18.从某服装厂即将出售的一批休闲装中抽检200件,其中不合格的休闲装有15件.
(1)抽检中合格的频数,频率分别是多少?
(2)销售3000套这样的休闲装,大约有多少件不合格的休闲装?
【分析】(1)利用频数和频率定义进行计算;
(2)利用样本估计总体的方法进行计算即可.
【解答】解:(1)合格的频数为200﹣15=185,
频率:185÷200=0.925;
(2)3000×=225(件).
答:大约有225件不合格的休闲装.
【点评】此题主要考查了频数与频率,关键是掌握频数是指每个对象出现的次数.频率是指每个对象出现的次数与总次数的比值(或者百分比).即频率=频数÷总数.同时考查了用样本估计总体.
19.学校为了了解学生每周体育锻炼时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表,请根据图表信息解答下列问题:
时间(小时) 频数(人数) 频率
2≤x<3 4 0.1
3≤x<4 10 0.25
4≤x<5 a 0.15
5≤x<6 8 b
6≤x<7 12 0.3
合计 1
(1)这次被调查的人数共有 40 人,表中的a= 6 ,b= 0.2 ;
(2)请将频数分布直方图补全;
(3)若该校共有1600名学生,试估计全校每周参加体育锻炼时间不低于4小时的学生约为多少名?
【分析】(1)根据题意列式计算即可;
(2)根据b的值画出直方图即可;
(3)利用样本估计总体的思想解决问题即可.
【解答】解:(1)总人数=4÷0.1=40,
∴a=40×0.15=6,b==0.2;
故答案为:6,0.2;
(2)频数分布直方图如图所示:
(3)由题意得,估计全校每周在校参加体育锻炼时间至少有4小时的学生约为1600×(0.15+0.2+0.3)=1040(名).
故估计全校每周参加体育锻炼时间不低于4小时的学生约为780名.
【点评】本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,认真观察、分析、研究统计图,作出正确的判断是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
课堂分层优化系列之基础提升练10.2直方图(一)
一.选择题(共8小题,每小题4分,共32分)
1.如图是某组15名学生数学测试成绩的频数分布直方图,则成绩低于60分的人数是( )
A.3人 B.6人 C.10人 D.14人
2.列一组数据的频数分布表时,落在各个小组内的数据的个数叫做( )
A.组距 B.频数 C.频率 D.样本容量
3.下列5个实数、、π、、中,无理数出现的频数是( )
A.2 B.3 C.4 D.5
4.某校对1200名女生的身高进行了测量,身高在1.58m~1.63m这一小组的频率为0.25,则该组共有( )
A.400人 B.300人 C.200人 D.100人
5.某篮球队员在一次训练中共投篮80次,命中了其中的64次,该运动员在这次训练中投篮命中的频率为( )
A.0.64 B.0.8 C.1.25 D.64
6.给出下面一组数据:19,20,25,31,28,27,26,21,20,22,24,23,25,29,27,28,27,30,18,20.若组距为2,则这组数据应分成( )组.
A.4 B.5 C.6 D.7
7.一组数据的最大值是132,最小值是89,将这组数据进行分组时,取组距为5,则组数是( )
A.7 B.8 C.9 D.10
8.如图是某班45名同学爱心捐款额的频数分布直方图(每组含前一个边界值,不含后一个边界值),则捐款人数最少的一组是( )
A.5~10元 B.10~15元 C.15~20元 D.20~25元
二.填空题(共5小题,每小题4分,共20分)
9.某校为了解七年级450名学生每周课外阅读情况,随机抽取该年级45名学生进行调查,绘制了如图频数分布直方图.可以估计该年级阅读时间不少于6小时的学生约有 人.
10.将100个数据分组绘制成频数分布直方图后发现,各小长方形高的比为2:4:3:1,那么第二组的频数是 .
11.某校有2000名学生,随机从中抽取50名学生,测出他们的体重(单位:kg),并整理绘制成频数分布表,其中
50.5≤x<55.5这组中共有12个数据,那么这次抽取的样本容量是 .
12.如图是某班级的一次数学考试成绩统计图,则得分及格(≥60分)的人数为 人.
13.为了解新冠肺炎疫情解封后刚复学时学生的心理健康,扬州市某区在全区7600名初中同学中随机抽查了500名同学进行问卷调查,对500个数据进行整理,在频数的统计表中各组的频数之和等于 .
三.解答题(共6小题,每小题8分,共48分)
14.一只不透明的袋中装有红球和黄球,全班同学都按序在袋中任意摸出1只球再放回袋内(摸球之前要搅匀),最后发现同学们摸到红球的频率比黄球大.这可能是什么原因?
15.为了让更多的失学儿童重返校园,某社区组织“献爱心手拉手”捐款活动.对社区部分捐款户数进行调查和分组统计后,将数据整理成如图所示的统计图(图中信息不完整).已知A、B两组捐款户数的比为1:5.
捐款户数分组统计表
组别 捐款额(x)元 户数
A 1≤x<100 a
B 100≤x<200 10
C 200≤x<300
D 300≤x<400
E x≥400
请结合以上信息解答下列问题
(1)a= ,本次调查样本的容量是 ;
(2)补全“捐款户数分组统计图1”;
(3)若该社区有500户住户,请根据以上信息估计,全社区捐款不少于300元的户数是多少?
16.为了增强同学们垃圾分类的意识,我校了举行一场学生在线参与垃圾分类处理知识测试.学校从八年级2000名学生中随机抽取部分学生的成绩,并将调查数据进行如下整理.
抽取的部分学生测试成绩的频数分布表:
成绩a(分) 频数(人) 频率
50≤a<60 10 0.1
60≤a<70 15 n
70≤a<80 m 0.2
80≤a<90 40 0.4
90≤a<100 15 0.15
由图表中给出的信息回答下列问题:
(1)m= ,n= ;
(2)补全频数分布直方图;
(3)如果成绩在80分以上(包括80分)为优秀,估计全校八年级2000名学生中成绩为优秀的人数.
17.为了让学生了解防疫知识,增强防疫意识,某市在中学生中进行了一次“防疫知识竞赛”,共有19000名中学生参加了这次竞赛.为了解本次竞赛的成绩情况,从中随机抽取了500名学生的成绩x(得分均为整数,满分100分)进行统计后得到下表.请根据表格解答下列问题:
分组 频数 频率
51≤x<61 40 0.08
61≤x<71 0.16
71≤x<81 100
81≤x<91 160 0.32
91≤x<101
合计 500
(1)补全表格;
(2)假设成绩在71分至90分之间(含71分,90分)的学生为二等奖,请据此估计该市获得二等奖的学生人数.
18.从某服装厂即将出售的一批休闲装中抽检200件,其中不合格的休闲装有15件.
(1)抽检中合格的频数,频率分别是多少?
(2)销售3000套这样的休闲装,大约有多少件不合格的休闲装?
19.学校为了了解学生每周体育锻炼时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表,请根据图表信息解答下列问题:
时间(小时) 频数(人数) 频率
2≤x<3 4 0.1
3≤x<4 10 0.25
4≤x<5 a 0.15
5≤x<6 8 b
6≤x<7 12 0.3
合计 1
(1)这次被调查的人数共有 人,表中的a= ,b= ;
(2)请将频数分布直方图补全;
(3)若该校共有1600名学生,试估计全校每周参加体育锻炼时间不低于4小时的学生约为多少名?
课堂分层优化系列之基础提升练10.2直方图(一)
参考答案与试题解析
一.选择题(共8小题,每小题4分,共32分)
1.如图是某组15名学生数学测试成绩的频数分布直方图,则成绩低于60分的人数是( )
A.3人 B.6人 C.10人 D.14人
【分析】根据直方图中的数据,可以得到成绩低于60分的人数,本题得以解决.
【解答】解:由直方图可知,
成绩低于60分的人数是1+2=3,
故选:A.
【点评】本题考查频数分布直方图,解答本题的关键是明确题意,利用数形结合的思想解答.
2.列一组数据的频数分布表时,落在各个小组内的数据的个数叫做( )
A.组距 B.频数 C.频率 D.样本容量
【分析】根据频数的定义,即落在各个小组内的数据的个数,可知B是答案.
【解答】解:由于频数是指落在各个小组内的数据的个数,故选B.
【点评】本题考查频数的定义,即落在各个小组内的数据的个数.
3.下列5个实数、、π、、中,无理数出现的频数是( )
A.2 B.3 C.4 D.5
【分析】根据频数的定义解决问题即可.
【解答】解:在、、π、、中,无理数有:、、π,无理数出现的频数是3.
故选:B.
【点评】本题考查频数与频率,有理数,无理数等知识,解题的关键是理解频数的定义.
4.某校对1200名女生的身高进行了测量,身高在1.58m~1.63m这一小组的频率为0.25,则该组共有( )
A.400人 B.300人 C.200人 D.100人
【分析】根据频率=频数÷总数,得:频数=总数×频率,进而即可求解.
【解答】解:根据题意,该组的人数为1200×0.25=300(人).
故选:B.
【点评】本题考查了频率的计算公式,理解公式.频率等于频数除以总数,能够灵活运用是关键.
5.某篮球队员在一次训练中共投篮80次,命中了其中的64次,该运动员在这次训练中投篮命中的频率为( )
A.0.64 B.0.8 C.1.25 D.64
【分析】根据频率的公式:频率=即可直接求解.
【解答】解:该运动员在这次训练中投篮命中的频率为=0.8.
故选:B.
【点评】本题考查了频率的计算公式,理解公式是关键.
6.给出下面一组数据:19,20,25,31,28,27,26,21,20,22,24,23,25,29,27,28,27,30,18,20.若组距为2,则这组数据应分成( )组.
A.4 B.5 C.6 D.7
【分析】用极差除以组距,如果商是整数,组数=这个整数加1,如果商不是整数,用进一法,确定组数.
【解答】解:∵(31﹣18)÷2=6.5,
∴分成的组数是7组,
故选:D.
【点评】本题考查频数分布直方图、组距、极差,组数之间的关系等知识,掌握组数的定义是本题的关键,即数据分成的组的个数称为组数.
7.一组数据的最大值是132,最小值是89,将这组数据进行分组时,取组距为5,则组数是( )
A.7 B.8 C.9 D.10
【分析】根据组数=(最大值﹣最小值)÷组距进行计算即可,注意小数部分要进位.
【解答】解:∵数据的最大值是132,最小值是89,
∴极差为132﹣89=43,
又∵组距为5,
∴43÷5=8.6,
∴组数为9,
故选:C.
【点评】此题考查了列频数分布表时组数的计算,掌握组数的定义是本题的关键,即数据分成的组的个数称为组数.
8.如图是某班45名同学爱心捐款额的频数分布直方图(每组含前一个边界值,不含后一个边界值),则捐款人数最少的一组是( )
A.5~10元 B.10~15元 C.15~20元 D.20~25元
【分析】根据直方图中的数据可以解答本题.
【解答】解:由直方图可得,捐款人数最少的一组是5~10元,只有5个人,
故选:A.
【点评】本题考查频数分布直方图,解答本题的关键是明确题意,读懂频数分布直方图.
二.填空题(共5小题)
9.某校为了解七年级450名学生每周课外阅读情况,随机抽取该年级45名学生进行调查,绘制了如图频数分布直方图.可以估计该年级阅读时间不少于6小时的学生约有 200 人.
【分析】根据图表数据,利用总人数乘以阅读时间不少于6小时的学生所占的百分数即可求解.
【解答】解:由图可知阅读时间不少于6小时的学生为450×=200(人).
故答案为:200.
【点评】本题考查读频数分布直方图的能力和利用统计图获取信息的能力.
10.将100个数据分组绘制成频数分布直方图后发现,各小长方形高的比为2:4:3:1,那么第二组的频数是 40 .
【分析】频数分布直方图中,各个长方形的高之比依次为2:4:3:1,则指各组频数之比为2:4:3:1,据此即可求出第二小组的频数
【解答】解:∵频数分布直方图中各个长方形的高之比依次为2:4:3:1,样本容量为100,
∴第二小组的频数为100×=40.
故答案为:40.
【点评】此题考查了频数(率)分布直方图,要知道,频数分布直方图中各个长方形的高之比即为各组频数之比.
11.某校有2000名学生,随机从中抽取50名学生,测出他们的体重(单位:kg),并整理绘制成频数分布表,其中
50.5≤x<55.5这组中共有12个数据,那么这次抽取的样本容量是 50 .
【分析】根据样本容量的定义:一个样本包括的个体数量叫做样本容量,即可得出答案.
【解答】解:样本容量:一个样本包括的个体数量叫做样本容量.样本容量只是个数字,没有单位.
故答案为:50.
【点评】本题考查了样本容量的定义,正确理解定义的关键.
12.如图是某班级的一次数学考试成绩统计图,则得分及格(≥60分)的人数为 36 人.
【分析】根据频数分布直方图中的数据可以得出得分及格(≥60分)的人数.
【解答】解:得分及格(≥60分)的人数为12+14+8+2=36(人),
故答案为:36.
【点评】本题考查频数分布直方图,解答本题的关键是利用数形结合的思想解答.
13.为了解新冠肺炎疫情解封后刚复学时学生的心理健康,扬州市某区在全区7600名初中同学中随机抽查了500名同学进行问卷调查,对500个数据进行整理,在频数的统计表中各组的频数之和等于 500 .
【分析】根据各小组频数之和等于数据总和可求得结果.
【解答】解:为了解新冠肺炎疫情解封后刚复学时学生的心理健康,扬州市某区在全区7600名初中同学中随机抽查了500名同学进行问卷调查,对500个数据进行整理,在频数的统计表中各组的频数之和等于500.
故答案为:500.
【点评】本题是对频率与频数灵活运用的综合考查,各小组频数之和等于数据总和,而各小组频率之和为1.
三.解答题(共6小题)
14.一只不透明的袋中装有红球和黄球,全班同学都按序在袋中任意摸出1只球再放回袋内(摸球之前要搅匀),最后发现同学们摸到红球的频率比黄球大.这可能是什么原因?
【分析】根据球的个数和实验条件解答即可.
【解答】解:摸到红球的可能性比黄球大,说明这个袋中红球比黄球多.
【点评】本题考查了频率和频数以及可能性大小的比较:只要总情况数目相同,谁包含的情况数目多,谁的可能性就大;反之也成立;若包含的情况相当,那么它们的可能性就相等.注意实验条件不同得到的结论也不同.
15.为了让更多的失学儿童重返校园,某社区组织“献爱心手拉手”捐款活动.对社区部分捐款户数进行调查和分组统计后,将数据整理成如图所示的统计图(图中信息不完整).已知A、B两组捐款户数的比为1:5.
捐款户数分组统计表
组别 捐款额(x)元 户数
A 1≤x<100 a
B 100≤x<200 10
C 200≤x<300
D 300≤x<400
E x≥400
请结合以上信息解答下列问题
(1)a= 2 ,本次调查样本的容量是 50 ;
(2)补全“捐款户数分组统计图1”;
(3)若该社区有500户住户,请根据以上信息估计,全社区捐款不少于300元的户数是多少?
【分析】(1)根据B组的户数和所占的份数,计算每一份有2户,A组的频数是2,样本的容量=A、B两组捐款户数÷A、B两组捐款户数所占的百分比;
(2)C组的频数=样本的容量×C组所占的百分比;
(3)捐款不少于300元的有D、E两组,捐款不少于300元的户数=500×D、E两组捐款户数所占的百分比;
【解答】解:(1)A组的频数是:
(10÷5)×1=2;
调查样本的容量是:
(10+2)÷(1﹣40%﹣28%﹣8%)=50,
故答案为:2,50;
(2)C组的频数是:50×40%=20,如图.
(3)∵500×(28%+8%)=180,
∴全社区捐款不少于300元的户数是180户;
答:估计全社区捐款不少于300元的户数是180户.
【点评】本题考查读频数分布直方图的能力和利用统计图获取信息的能力.利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
16.为了增强同学们垃圾分类的意识,我校了举行一场学生在线参与垃圾分类处理知识测试.学校从八年级2000名学生中随机抽取部分学生的成绩,并将调查数据进行如下整理.
抽取的部分学生测试成绩的频数分布表:
成绩a(分) 频数(人) 频率
50≤a<60 10 0.1
60≤a<70 15 n
70≤a<80 m 0.2
80≤a<90 40 0.4
90≤a<100 15 0.15
由图表中给出的信息回答下列问题:
(1)m= 20 ,n= 0.15 ;
(2)补全频数分布直方图;
(3)如果成绩在80分以上(包括80分)为优秀,估计全校八年级2000名学生中成绩为优秀的人数.
【分析】(1)先求出样本容量,再根据频率=频数÷样本容量求解即可得出答案;
(2)根据所求m的值即可补全图形;
(3)总人数乘以成绩在80分以上(包括80分)的人数所占比例即可.
【解答】解:(1)∵样本容量为10÷0.1=100,
∴m=100×0.2=20,n=15÷100=0.15,
故答案为:20、0.15;
(2)补全直方图如下:
(3)2000×(0.4+0.15)=1100(人),
答:估计全校八年级2000名学生中成绩为优秀的人数约为1100人.
【点评】本题考查频数分布直方图、频数分布表,解答本题的关键是明确题意,利用数形结合的思想解答.
17.为了让学生了解防疫知识,增强防疫意识,某市在中学生中进行了一次“防疫知识竞赛”,共有19000名中学生参加了这次竞赛.为了解本次竞赛的成绩情况,从中随机抽取了500名学生的成绩x(得分均为整数,满分100分)进行统计后得到下表.请根据表格解答下列问题:
分组 频数 频率
51≤x<61 40 0.08
61≤x<71 0.16
71≤x<81 100
81≤x<91 160 0.32
91≤x<101
合计 500
(1)补全表格;
(2)假设成绩在71分至90分之间(含71分,90分)的学生为二等奖,请据此估计该市获得二等奖的学生人数.
【分析】(1)频率=频数÷总数、频数之和等于总数求解即可;
(2)用总人数乘以对应频率之和即可.
【解答】解(1)根据频率=频数÷总数得:500×0.16=80,100÷500=0.2,500﹣40﹣80﹣100﹣160=120,120÷500=0.24,
故表格如图所示:
分组 频数 频率
51≤x<61 40 0.08
61≤x<71 80 0.16
71≤x<81 100 0.2
81≤x<91 160 0.32
91≤x<101 120 0.24
合计 500 1
(2)故估计该市获得二等奖的学生人数为:19000×(0.2+0.32)=9880(人),
答:估计该市获得二等奖的学生人数为9880人.
【点评】本题主要考查频数(率)分布表,解题的关键是掌握频率=频数÷总数、频数之和等于总数.
18.从某服装厂即将出售的一批休闲装中抽检200件,其中不合格的休闲装有15件.
(1)抽检中合格的频数,频率分别是多少?
(2)销售3000套这样的休闲装,大约有多少件不合格的休闲装?
【分析】(1)利用频数和频率定义进行计算;
(2)利用样本估计总体的方法进行计算即可.
【解答】解:(1)合格的频数为200﹣15=185,
频率:185÷200=0.925;
(2)3000×=225(件).
答:大约有225件不合格的休闲装.
【点评】此题主要考查了频数与频率,关键是掌握频数是指每个对象出现的次数.频率是指每个对象出现的次数与总次数的比值(或者百分比).即频率=频数÷总数.同时考查了用样本估计总体.
19.学校为了了解学生每周体育锻炼时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表,请根据图表信息解答下列问题:
时间(小时) 频数(人数) 频率
2≤x<3 4 0.1
3≤x<4 10 0.25
4≤x<5 a 0.15
5≤x<6 8 b
6≤x<7 12 0.3
合计 1
(1)这次被调查的人数共有 40 人,表中的a= 6 ,b= 0.2 ;
(2)请将频数分布直方图补全;
(3)若该校共有1600名学生,试估计全校每周参加体育锻炼时间不低于4小时的学生约为多少名?
【分析】(1)根据题意列式计算即可;
(2)根据b的值画出直方图即可;
(3)利用样本估计总体的思想解决问题即可.
【解答】解:(1)总人数=4÷0.1=40,
∴a=40×0.15=6,b==0.2;
故答案为:6,0.2;
(2)频数分布直方图如图所示:
(3)由题意得,估计全校每周在校参加体育锻炼时间至少有4小时的学生约为1600×(0.15+0.2+0.3)=1040(名).
故估计全校每周参加体育锻炼时间不低于4小时的学生约为780名.
【点评】本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,认真观察、分析、研究统计图,作出正确的判断是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
