2023版新教材高中数学单元素养测评卷一 第六章 平面向量及其应用(含解析)
文档属性
| 名称 | 2023版新教材高中数学单元素养测评卷一 第六章 平面向量及其应用(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 120.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-11 00:00:00 | ||
图片预览




文档简介
单元素养测评卷(一)
时间:120分钟 满分:150分
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.下列命题正确的是( )
A.若a,b都是单位向量,则a=b
B.若向量a∥b,b∥c,则a∥c
C.与非零向量a共线的单位向量是唯一的
D.已知λ,μ为非零实数,若λa=μb,则a与b共线
2.下列等式中一定成立的是( )
A.+= B.-=
C.+=0 D.++=0
3.在△ABC中,若c2=a2+b2+ab,则∠C=( )
A.60° B.120°
C.135° D.150°
4.已知点A(1,2),B(3,2),C(3,4),则向量在方向上的投影向量为( )
A.(,) B.(1,1)C.(2,2) D.(,)
5.若△ABC的三个内角满足sin A∶sin B∶sin C=5∶12∶13,则△ABC是( )
A.钝角三角形 B.直角三角形
C.等边三角形 D.等腰直角三角形
6.如图,在平行四边形ABCD中,M为AB的中点,AC与DM交于点O,则=( )
A.=-
B.=-
C.=-
D.=-
7.在△ABC中,角A,B,C对应边分别为a,b,c,已知三个向量m=(a,cos ),n=(b,cos ),p=(c,cos )共线,则△ABC形状为( )
A.等边三角形 B.等腰三角形
C.直角三角形 D.等腰直角三角形
8.如图,O是△ABC的重心,D是边BC上一点,且=3,=λ+μ,则=( )
A.- B.-C. D.
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有错选的得0分.
9.已知向量a=(-1,2),b=(2,3),则( )
A.a·b=4
B.(a+b)2=
C.(a+b)·(a-b)=-8
D.(a-b)2=10
10.已知a,b是单位向量,且a+b=(1,-1),则( )
A.a∥b
B.a与b垂直
C.a与a-b的夹角为
D.|a-b|=1
11.在△ABC中,a,b,c分别是内角A,B,C的对边,下列说法正确的是( )
A.若A为锐角,则b2+c2>a2
B.若A为锐角,则b+c2C.若sin A>sin B,则A>B
D.若sin A>sin B,则A与B大小不能确定
12.在△ABC中,下列正确的是( )
A.若·<0,则△ABC为钝角三角形
B.若=,则△ABC为直角三角形
C.若(+)·(-)=0,则△ABC为等腰三角形
D.已知++=0,且=||=||,则△ABC为等边三角形
三、填空题:本题共4小题,每小题5分,共20分.
13.设向量a=(m+1,m-1),b=(-1,m),c=(-1,1),若(2a+b)⊥c,则实数m=________.
14.已知|a|=,|b|=1,a·(a-b)=1,则向量a与向量b的夹角为________.
15.如图,在△ABC中,已知B=45°,D是边BC上一点,AD=10,AC=14,DC=6,则AB=________.
16.在△ABC中,AB=AC=,=2,2=,·=,则BC=________,若点P在线段CF上,则·的最大值为________.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题10分)已知a=(1,0),b=(2,1).
(1)当k为何值时,ka-b与a+2b共线;
(2)若=2a+3b,=a+mb,且A,B,C三点共线,求m的值.
18.(本小题12分)设△ABC内角A,B,C的对边分别为a,b,c,已知(2b-a)cos C=c cos A.
(1)求角C的大小;
(2)若c=2,且________,求△ABC的周长.
请在下列三个条件中,选择其中的一个条件补充到上面的横线中,并完成作答.
①△ABC的面积为;②·=;③sin A sin B=.
注:如果选择多个条件分别解答,那么按第一解答计分.
19.(本小题12分)已知四边形ABCD中,∠A=60°,∠ADC=90°,AB=2,BD=2,DC=4.
(1)求sin ∠ADB;
(2)求BC.
20.(本小题12分)已知向量a=(,1),a·b=4.
(1)当|b|=4时,求;
(2)求|b|的最小值,并求此时向量a,b的夹角大小.
21.(本小题12分)在△ABC中,内角A,B,C所对的边分别为a,b,c,c-b=a cos B-b cos A.
(1)求A;
(2)若a=4,求△ABC面积的最大值.
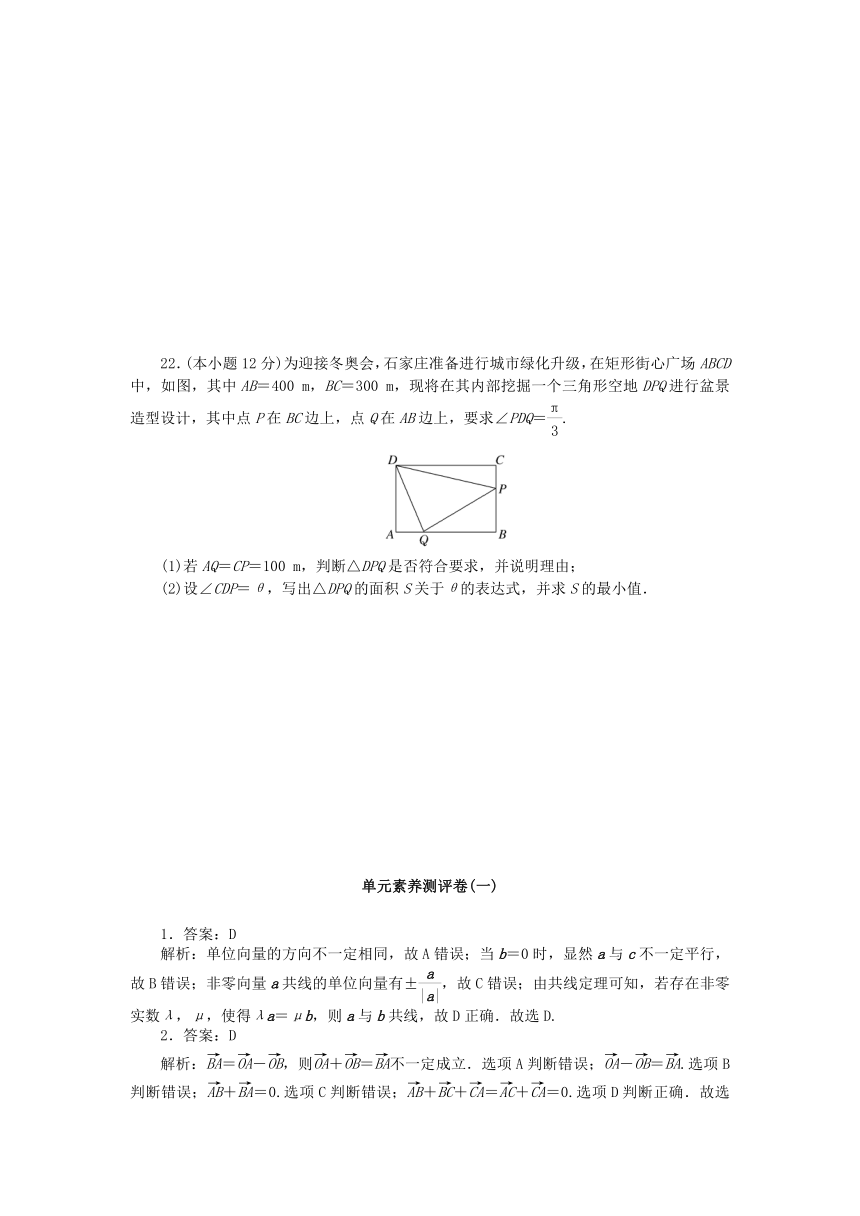
22.(本小题12分)为迎接冬奥会,石家庄准备进行城市绿化升级,在矩形街心广场ABCD中,如图,其中AB=400 m,BC=300 m,现将在其内部挖掘一个三角形空地DPQ进行盆景造型设计,其中点P在BC边上,点Q在AB边上,要求∠PDQ=.
(1)若AQ=CP=100 m,判断△DPQ是否符合要求,并说明理由;
(2)设∠CDP=θ,写出△DPQ的面积S关于θ的表达式,并求S的最小值.
单元素养测评卷(一)
1.答案:D
解析:单位向量的方向不一定相同,故A错误;当b=0时,显然a与c不一定平行,故B错误;非零向量a共线的单位向量有±,故C错误;由共线定理可知,若存在非零实数λ,μ,使得λa=μb,则a与b共线,故D正确.故选D.
2.答案:D
解析:=-,则+=不一定成立.选项A判断错误;-=.选项B判断错误;+=0.选项C判断错误;++=+=0.选项D判断正确.故选D.
3.答案:B
解析:由c2=a2+b2+ab,得a2+b2-c2=-ab,cos C===-,由于0°4.答案:B
解析:=(2,0),=(2,2),则向量在方向上的投影向量为·=·=(1,1),故选B.
5.答案:B
解析:由正弦定理可得a∶b∶c=5∶12∶13,令a=5t,b=12t,c=13t,则c为最长的边,故角C最大,
由余弦定理可得cos C==0,所以角C为直角.
故△ABC是直角三角形.故选B.
6.答案:A
解析:设=x,
则=x=x=2x+x,
因为O,D,M三点共线,
所以2x+x=1,解得x=,
则=x=+,
所以=+=--+=-.
故选A.
7.答案:A
解析:∵向量m=(a,cos ),n=(b,cos )共线,
∴a cos =b cos .
由正弦定理得:sin A cos =sin B cos .
∴2sin cos cos =2sin cos cos .
∵0<<,0<<,
所以cos ≠0,cos ≠0,
则sin =sin .
∴=,即A=B.
同理由n=,p=共线,可得B=C.
∴△ABC形状为等边三角形.
故选A.
8.答案:A
解析:如图,延长AO交BC于E,由已知O为△ABC的重心,
则点E为BC的中点,且=2,=(+).
由=3,得D是BC的四等分点,
则=+=+=×(+)+(-)=-+,所以λ=-,μ=,所以=-.
故选A.
9.答案:ACD
解析:因为a·b=-1×2+2×3=4,故A正确;因为a+b=(1,5),a-b=(-3,-1),所以(a+b)2=26,(a-b)2=10,故B错误,D正确;(a+b)·(a-b)=-8,故C正确.
故选ACD.
10.答案:BC
解析:因为a+b=(1,-1),
所以==,a2=|a|2=1,b2=|b|2=1,
2=a2+b2+2a·b=2,
所以a·b=0,所以a⊥b,故B正确,A错误;
====,
因为a·(a-b)=a2-a·b=1,
所以cos 〈a,a-b〉===,
所以a与a-b的夹角为,故C正确,D错误.
故选BC.
11.答案:AC
解析:对AB,A为锐角,cos A>0,由余弦定理得a2=b2+c2-2bc cos A对CD,A,B∈,sin A>sin B>0,由正弦定理得=,故=<1,故b12.答案:BCD
解析:对A,·<0即·>0,即||·||·cos A>0,可得cos A>0,不能证明△ABC为钝角三角形,故A错误;
对B,|+|=|-|即2+2+2·=2+2-2·,
解得·=0,故∠A=90°,故B正确;
对C,若(+)·(-)=0,则2-2=0,故||=||,故△ABC为等腰三角形,故C正确;
对D,因为++=0,故|+|2=|-|2,即||2+||2+2·=||2,又||=||=||,
所以||2+2||·||cos ∠AOB=0,故cos ∠AOB=-,故∠AOB=120°,同理∠AOB=∠AOC=∠BOC=120°,结合||=||=||可得||=||=||,故△ABC为等边三角形,故D正确.
故选BCD.
13.答案:3
解析:因为a=(m+1,m-1),b=(-1,m),c=(-1,1),所以2a+b=(2m+1,3m-2),
又(2a+b)⊥c,故(2a+b)·c=0,即-(2m+1)+(3m-2)=0,解得m=3.
14.答案:
解析:设向量a与向量b的夹角为θ,
因为|a|=,|b|=1,a·(a-b)=1,
所以a2-a·b=|a|2-|a||b|cos θ=2-cos θ=1,
得cos θ=,
因为θ∈[0,π],所以θ=.
15.答案:5
解析:由题,在△ADC中,cos C===,
所以sin C==,
在△ABC中,=,即=,所以AB=5.
16.答案:
解析:由题,因为=2,所以=2,
又2=,则=,
因为=+=+,=-=2-,
则·=(+)·(2-)=22-2+·=,
因为AB=AC=,则2×()2-()2+·=,所以·=,
所以BC=||===;
因为点P在线段CF上,所以设=λ,λ∈[0,1],
因为=+=+λ=+λ,
所以·=(+λ)·(-)=2+(λ-1)·-λ2=-λ+,
所以当λ=0时,·的最大值为.
17.解析:(1)由a=(1,0),b=(2,1),可得ka-b=k(1,0)-(2,1)=(k-2,-1),
a+2b=(1,0)+2(2,1)=(5,2),
因为ka-b与a+2b共线,所以2(k-2)-(-1)×5=0,
即2k-4+5=0,解得k=-.
(2)因为A,B,C三点共线,所以=λ,λ∈R,
即2a+3b=λ(a+mb),所以,解得m=.
18.解析:(1)因为(2b-a)cos C=c cos A,
由正弦定理可得(2sin B-sin A)cos C=sin C cos A,
所以2sin B cos C=sin (A+C)=sin B,
在△ABC中,sin B>0,
所以cos C=,因为C∈(0,π),
所以C=.
(2)若选①,因为△ABC的面积为,
所以ab sin C=ab sin =ab=,
所以ab=.
若选②,因为·=,
所以ab cos C=ab cos =ab=,
所以ab=.
若选③,由正弦定理====4,
所以sin A=,sin B=,
因为sin A sin B=.
所以ab=,
由余弦定理得c2=a2+b2-2ab cos 60°=a2+b2-ab,
即(a+b)2-3ab=12,
所以(a+b)2=16,则a+b=4或a+b=-4(舍去),
所以△ABC的周长为a+b+c=4+2.
19.解析:(1)在△ABD中,由正弦定理可知=,
即=,解得sin ∠ADB=.
(2)由∠ADC=90°,故cos ∠BDC=cos (90°-∠ADB)=sin ∠ADB=,
在△CBD中,由余弦定理得BC2=DC2+BD2-2DC·BD cos ∠BDC,
即BC2=(4)2+(2)2-2×4×2×=48,
所以BC=4.
20.解析:(1)因为a=(,1) |a|==2.
因为|a+b|2=a2+2a·b+b2=4+8+16=28,
所以|a+b|=2.
(2)解法1:设〈a,b〉=θ,
因为a·b=4>0,
所以θ∈,
由a·b=|a||b|cos θ=4 |b|==≥2,
当且仅当cos θ=1即θ=0时取等;
所以|b|最小值为2,此时a,b夹角大小为0.
解法2:设b=(x,y),
由a·b=4 x+y=4,
所以|b|==
== ;
故当x=,y=1时|b|最小值为2,
此时cos 〈a,b〉==1 〈a,b〉=0.
21.解析:(1)∵c-b=a cos B-b cos A,∴sin C-sin B=sin A cos B-sin B cos A,
则sin A cos B+sin B cos A-sin B=sin A cos B-sin B cos A,
即2sin B cos A=sin B.
因为sin B≠0,所以cos A=,
又∵0(2)由余弦定理得a2=b2+c2-2bc cos A,即16=b2+c2-bc≥2bc-bc=bc,
所以bc≤16,当且仅当b=c=4时,等号成立.
S△ABC=bc sin A=bc≤4,
故△ABC面积的最大值为4.
22.解析:(1)由题意,某城市有一矩形街心广场ABCD,其中AB=4百米,BC=3百米,
现将在其内部挖掘一个三角形水池DPQ进行盆景造型设计,
其中点P在BC边上,点Q在AB边上,要求∠PDQ=因为AQ=CP=1百米,
可得BQ=3百米,BP=2百米,
所以PQ=百米,DQ=百米,DP=百米,
在△DPQ中,
可得cos ∠PDQ==≠=cos ,所以∠PDQ≠,
所以△PDQ不符合要求.
(2)因为∠CDP=θ且∠PDQ=,可得∠ADQ=-θ,
所以DP=,DQ=,
所以△DPQ的面积为:S=DP·DQ·sin =××=,
又因为cos θcos (-θ)=cos θ(cos θ+sin θ)=cos2θ+sinθcos θ=·+sin 2θ=+sin (2θ+)≤+,
所以S≥240 000-360 000,即S的最小值120 000·(2-) m2.
时间:120分钟 满分:150分
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.下列命题正确的是( )
A.若a,b都是单位向量,则a=b
B.若向量a∥b,b∥c,则a∥c
C.与非零向量a共线的单位向量是唯一的
D.已知λ,μ为非零实数,若λa=μb,则a与b共线
2.下列等式中一定成立的是( )
A.+= B.-=
C.+=0 D.++=0
3.在△ABC中,若c2=a2+b2+ab,则∠C=( )
A.60° B.120°
C.135° D.150°
4.已知点A(1,2),B(3,2),C(3,4),则向量在方向上的投影向量为( )
A.(,) B.(1,1)C.(2,2) D.(,)
5.若△ABC的三个内角满足sin A∶sin B∶sin C=5∶12∶13,则△ABC是( )
A.钝角三角形 B.直角三角形
C.等边三角形 D.等腰直角三角形
6.如图,在平行四边形ABCD中,M为AB的中点,AC与DM交于点O,则=( )
A.=-
B.=-
C.=-
D.=-
7.在△ABC中,角A,B,C对应边分别为a,b,c,已知三个向量m=(a,cos ),n=(b,cos ),p=(c,cos )共线,则△ABC形状为( )
A.等边三角形 B.等腰三角形
C.直角三角形 D.等腰直角三角形
8.如图,O是△ABC的重心,D是边BC上一点,且=3,=λ+μ,则=( )
A.- B.-C. D.
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有错选的得0分.
9.已知向量a=(-1,2),b=(2,3),则( )
A.a·b=4
B.(a+b)2=
C.(a+b)·(a-b)=-8
D.(a-b)2=10
10.已知a,b是单位向量,且a+b=(1,-1),则( )
A.a∥b
B.a与b垂直
C.a与a-b的夹角为
D.|a-b|=1
11.在△ABC中,a,b,c分别是内角A,B,C的对边,下列说法正确的是( )
A.若A为锐角,则b2+c2>a2
B.若A为锐角,则b+c2
D.若sin A>sin B,则A与B大小不能确定
12.在△ABC中,下列正确的是( )
A.若·<0,则△ABC为钝角三角形
B.若=,则△ABC为直角三角形
C.若(+)·(-)=0,则△ABC为等腰三角形
D.已知++=0,且=||=||,则△ABC为等边三角形
三、填空题:本题共4小题,每小题5分,共20分.
13.设向量a=(m+1,m-1),b=(-1,m),c=(-1,1),若(2a+b)⊥c,则实数m=________.
14.已知|a|=,|b|=1,a·(a-b)=1,则向量a与向量b的夹角为________.
15.如图,在△ABC中,已知B=45°,D是边BC上一点,AD=10,AC=14,DC=6,则AB=________.
16.在△ABC中,AB=AC=,=2,2=,·=,则BC=________,若点P在线段CF上,则·的最大值为________.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题10分)已知a=(1,0),b=(2,1).
(1)当k为何值时,ka-b与a+2b共线;
(2)若=2a+3b,=a+mb,且A,B,C三点共线,求m的值.
18.(本小题12分)设△ABC内角A,B,C的对边分别为a,b,c,已知(2b-a)cos C=c cos A.
(1)求角C的大小;
(2)若c=2,且________,求△ABC的周长.
请在下列三个条件中,选择其中的一个条件补充到上面的横线中,并完成作答.
①△ABC的面积为;②·=;③sin A sin B=.
注:如果选择多个条件分别解答,那么按第一解答计分.
19.(本小题12分)已知四边形ABCD中,∠A=60°,∠ADC=90°,AB=2,BD=2,DC=4.
(1)求sin ∠ADB;
(2)求BC.
20.(本小题12分)已知向量a=(,1),a·b=4.
(1)当|b|=4时,求;
(2)求|b|的最小值,并求此时向量a,b的夹角大小.
21.(本小题12分)在△ABC中,内角A,B,C所对的边分别为a,b,c,c-b=a cos B-b cos A.
(1)求A;
(2)若a=4,求△ABC面积的最大值.
22.(本小题12分)为迎接冬奥会,石家庄准备进行城市绿化升级,在矩形街心广场ABCD中,如图,其中AB=400 m,BC=300 m,现将在其内部挖掘一个三角形空地DPQ进行盆景造型设计,其中点P在BC边上,点Q在AB边上,要求∠PDQ=.
(1)若AQ=CP=100 m,判断△DPQ是否符合要求,并说明理由;
(2)设∠CDP=θ,写出△DPQ的面积S关于θ的表达式,并求S的最小值.
单元素养测评卷(一)
1.答案:D
解析:单位向量的方向不一定相同,故A错误;当b=0时,显然a与c不一定平行,故B错误;非零向量a共线的单位向量有±,故C错误;由共线定理可知,若存在非零实数λ,μ,使得λa=μb,则a与b共线,故D正确.故选D.
2.答案:D
解析:=-,则+=不一定成立.选项A判断错误;-=.选项B判断错误;+=0.选项C判断错误;++=+=0.选项D判断正确.故选D.
3.答案:B
解析:由c2=a2+b2+ab,得a2+b2-c2=-ab,cos C===-,由于0°
解析:=(2,0),=(2,2),则向量在方向上的投影向量为·=·=(1,1),故选B.
5.答案:B
解析:由正弦定理可得a∶b∶c=5∶12∶13,令a=5t,b=12t,c=13t,则c为最长的边,故角C最大,
由余弦定理可得cos C==0,所以角C为直角.
故△ABC是直角三角形.故选B.
6.答案:A
解析:设=x,
则=x=x=2x+x,
因为O,D,M三点共线,
所以2x+x=1,解得x=,
则=x=+,
所以=+=--+=-.
故选A.
7.答案:A
解析:∵向量m=(a,cos ),n=(b,cos )共线,
∴a cos =b cos .
由正弦定理得:sin A cos =sin B cos .
∴2sin cos cos =2sin cos cos .
∵0<<,0<<,
所以cos ≠0,cos ≠0,
则sin =sin .
∴=,即A=B.
同理由n=,p=共线,可得B=C.
∴△ABC形状为等边三角形.
故选A.
8.答案:A
解析:如图,延长AO交BC于E,由已知O为△ABC的重心,
则点E为BC的中点,且=2,=(+).
由=3,得D是BC的四等分点,
则=+=+=×(+)+(-)=-+,所以λ=-,μ=,所以=-.
故选A.
9.答案:ACD
解析:因为a·b=-1×2+2×3=4,故A正确;因为a+b=(1,5),a-b=(-3,-1),所以(a+b)2=26,(a-b)2=10,故B错误,D正确;(a+b)·(a-b)=-8,故C正确.
故选ACD.
10.答案:BC
解析:因为a+b=(1,-1),
所以==,a2=|a|2=1,b2=|b|2=1,
2=a2+b2+2a·b=2,
所以a·b=0,所以a⊥b,故B正确,A错误;
====,
因为a·(a-b)=a2-a·b=1,
所以cos 〈a,a-b〉===,
所以a与a-b的夹角为,故C正确,D错误.
故选BC.
11.答案:AC
解析:对AB,A为锐角,cos A>0,由余弦定理得a2=b2+c2-2bc cos A
解析:对A,·<0即·>0,即||·||·cos A>0,可得cos A>0,不能证明△ABC为钝角三角形,故A错误;
对B,|+|=|-|即2+2+2·=2+2-2·,
解得·=0,故∠A=90°,故B正确;
对C,若(+)·(-)=0,则2-2=0,故||=||,故△ABC为等腰三角形,故C正确;
对D,因为++=0,故|+|2=|-|2,即||2+||2+2·=||2,又||=||=||,
所以||2+2||·||cos ∠AOB=0,故cos ∠AOB=-,故∠AOB=120°,同理∠AOB=∠AOC=∠BOC=120°,结合||=||=||可得||=||=||,故△ABC为等边三角形,故D正确.
故选BCD.
13.答案:3
解析:因为a=(m+1,m-1),b=(-1,m),c=(-1,1),所以2a+b=(2m+1,3m-2),
又(2a+b)⊥c,故(2a+b)·c=0,即-(2m+1)+(3m-2)=0,解得m=3.
14.答案:
解析:设向量a与向量b的夹角为θ,
因为|a|=,|b|=1,a·(a-b)=1,
所以a2-a·b=|a|2-|a||b|cos θ=2-cos θ=1,
得cos θ=,
因为θ∈[0,π],所以θ=.
15.答案:5
解析:由题,在△ADC中,cos C===,
所以sin C==,
在△ABC中,=,即=,所以AB=5.
16.答案:
解析:由题,因为=2,所以=2,
又2=,则=,
因为=+=+,=-=2-,
则·=(+)·(2-)=22-2+·=,
因为AB=AC=,则2×()2-()2+·=,所以·=,
所以BC=||===;
因为点P在线段CF上,所以设=λ,λ∈[0,1],
因为=+=+λ=+λ,
所以·=(+λ)·(-)=2+(λ-1)·-λ2=-λ+,
所以当λ=0时,·的最大值为.
17.解析:(1)由a=(1,0),b=(2,1),可得ka-b=k(1,0)-(2,1)=(k-2,-1),
a+2b=(1,0)+2(2,1)=(5,2),
因为ka-b与a+2b共线,所以2(k-2)-(-1)×5=0,
即2k-4+5=0,解得k=-.
(2)因为A,B,C三点共线,所以=λ,λ∈R,
即2a+3b=λ(a+mb),所以,解得m=.
18.解析:(1)因为(2b-a)cos C=c cos A,
由正弦定理可得(2sin B-sin A)cos C=sin C cos A,
所以2sin B cos C=sin (A+C)=sin B,
在△ABC中,sin B>0,
所以cos C=,因为C∈(0,π),
所以C=.
(2)若选①,因为△ABC的面积为,
所以ab sin C=ab sin =ab=,
所以ab=.
若选②,因为·=,
所以ab cos C=ab cos =ab=,
所以ab=.
若选③,由正弦定理====4,
所以sin A=,sin B=,
因为sin A sin B=.
所以ab=,
由余弦定理得c2=a2+b2-2ab cos 60°=a2+b2-ab,
即(a+b)2-3ab=12,
所以(a+b)2=16,则a+b=4或a+b=-4(舍去),
所以△ABC的周长为a+b+c=4+2.
19.解析:(1)在△ABD中,由正弦定理可知=,
即=,解得sin ∠ADB=.
(2)由∠ADC=90°,故cos ∠BDC=cos (90°-∠ADB)=sin ∠ADB=,
在△CBD中,由余弦定理得BC2=DC2+BD2-2DC·BD cos ∠BDC,
即BC2=(4)2+(2)2-2×4×2×=48,
所以BC=4.
20.解析:(1)因为a=(,1) |a|==2.
因为|a+b|2=a2+2a·b+b2=4+8+16=28,
所以|a+b|=2.
(2)解法1:设〈a,b〉=θ,
因为a·b=4>0,
所以θ∈,
由a·b=|a||b|cos θ=4 |b|==≥2,
当且仅当cos θ=1即θ=0时取等;
所以|b|最小值为2,此时a,b夹角大小为0.
解法2:设b=(x,y),
由a·b=4 x+y=4,
所以|b|==
== ;
故当x=,y=1时|b|最小值为2,
此时cos 〈a,b〉==1 〈a,b〉=0.
21.解析:(1)∵c-b=a cos B-b cos A,∴sin C-sin B=sin A cos B-sin B cos A,
则sin A cos B+sin B cos A-sin B=sin A cos B-sin B cos A,
即2sin B cos A=sin B.
因为sin B≠0,所以cos A=,
又∵0
所以bc≤16,当且仅当b=c=4时,等号成立.
S△ABC=bc sin A=bc≤4,
故△ABC面积的最大值为4.
22.解析:(1)由题意,某城市有一矩形街心广场ABCD,其中AB=4百米,BC=3百米,
现将在其内部挖掘一个三角形水池DPQ进行盆景造型设计,
其中点P在BC边上,点Q在AB边上,要求∠PDQ=因为AQ=CP=1百米,
可得BQ=3百米,BP=2百米,
所以PQ=百米,DQ=百米,DP=百米,
在△DPQ中,
可得cos ∠PDQ==≠=cos ,所以∠PDQ≠,
所以△PDQ不符合要求.
(2)因为∠CDP=θ且∠PDQ=,可得∠ADQ=-θ,
所以DP=,DQ=,
所以△DPQ的面积为:S=DP·DQ·sin =××=,
又因为cos θcos (-θ)=cos θ(cos θ+sin θ)=cos2θ+sinθcos θ=·+sin 2θ=+sin (2θ+)≤+,
所以S≥240 000-360 000,即S的最小值120 000·(2-) m2.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
