2023版新教材高中数学单元素养测评卷四 第九章 统计(含解析)
文档属性
| 名称 | 2023版新教材高中数学单元素养测评卷四 第九章 统计(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 381.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-11 00:00:00 | ||
图片预览


文档简介
单元素养测评卷(四)
时间:120分钟 满分:150分
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.下列情况适合用全面调查的是( )
A.了解一批玉米种子的发芽率
B.了解某城市居民的食品消费结构
C.调查一个县各村的粮食播种面积
D.调查一条河的水质
2.现有以下两项调查:①从100台刚出厂的电视机中抽取3台进行质量检查;②某社区有1 000户家庭,其中高收入家庭100户,中等收入家庭820户,低收入家庭80户,为了调查家庭每年生活费的开支情况,计划抽取一个容量为50的样本,则完成这两项调查最适宜采用的抽样方法分别是( )
A.①②都采用简单随机抽样
B.①②都采用分层随机抽样
C.①采用简单随机抽样,②采用分层随机抽样
D.①采用分层随机抽样,②采用简单随机抽样
3.现利用随机数法从高一(3)班的50名同学中选取5名同学参与学校活动.该班同学分别编号为01,02,…,49,50.选取方法是从随机数表第1行第6列的数开始由左到右依次选取两个数字,则选出来的第5个个体的编号为( )
(注:下表为随机数表的第1行和第2行)
7816 6572 0802 6314 0702 4369 9728 0198
3204 9243 4935 8200 3623 4869 6938 7481
A.31 B.40 C.36 D.24
4.已知某工厂生产A,B,C三种型号的零件,这三种型号的零件周产量之比为2∶3∶5,现在用分层抽样的方法从某周生产的零件中抽取若干个进行质量检查,若抽取C型号零件25个,则这三种型号的零件共抽取的个数为( )
A.50 B.55 C.60 D.65
5.幸福感指数是指某个人主观评价他对自己目前生活状态满意程度的指标,常用区间[0,10]内的一个数来表示,该数越接近10表示满意度越高.现随机抽取10位市民,他们的幸福感指数分别为6,6,7,7,8,8,8,9,9,10,则这组数据的80%分位数是( )
A.8 B.8.5 C.9 D.9.5
6.
某学校组建了合唱、朗诵、脱口秀、舞蹈、太极拳五个社团,该校共有2 000名同学,每名同学依据自己的兴趣爱好最多可参加其中一个,各个社团的人数比例的饼状图如图所示,其中参加朗诵社团的同学有8名,参加太极拳社团的有12名,则( )
A.这五个社团的总人数为100
B.脱口秀社团的人数占五个社团总人数的20%
C.这五个社团总人数占该校学生人数的8%
D.从这五个社团中任选一人,其来自脱口秀社团或舞蹈社团的概率为50%
7.为了解“双减”政策实施后学生每天的体育活动时间,研究人员随机调查了该地区1 000名学生每天进行体育运动的时间,按照时长(单位:分钟)分成6组:第一组[30,40),第二组[40,50),第三组[50,60),第四组[60,70),第五组[70,80),第六组[80,90],经整理得到如图的频率分布直方图,则可以估计该地区学生每天体育活动时间的第25百分位数约为( )
A.42.5分钟 B.45.5分钟 C.47.5分钟 D.50分钟
8.疫情期间,某校为了了解学生在线学习情况,统计了该校A,B两班2022年2月18日~2月26日每天在线学习人数情况,如图所示:
下列说法不正确的是( )
A.A班每天在线学习人数的中位数为34
B.记A班与B班每天在线学习人数的方差分别为s,s,则s>s
C.A班与B班每天在线学习人数之和不超过60的天数为3天
D.从20日~23日,A班与B班每天在线学习人数都在逐日减少
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.某公司生产三种型号的轿车,年产量分别为1 500辆、6 000辆和2 000辆.为检验产品质量,公司质检部门要抽取57辆进行检验,则下列说法正确的是( )
A.应采用分层随机抽样抽取
B.应采用抽签法抽取
C.三种型号的轿车依次应抽取9辆、36辆、12辆
D.这三种型号的轿车,每一辆被抽到的可能性相同
10.某学生5次考试的成绩(单位:分)分别为85,69,m,80,91,其中m>0.若该学生在这5次考试中成绩的中位数为80,则5次考试成绩的平均数可能为( )
A.76 B.80 C.81 D.85
11.一组数据x1,x2,…,xn的平均数是4,方差为3,关于数据3x1-1,3x2-1,…,3xn-1,下列说法正确的是( )
A.平均数是4 B.平均数是11
C.方差是8 D.方差是27
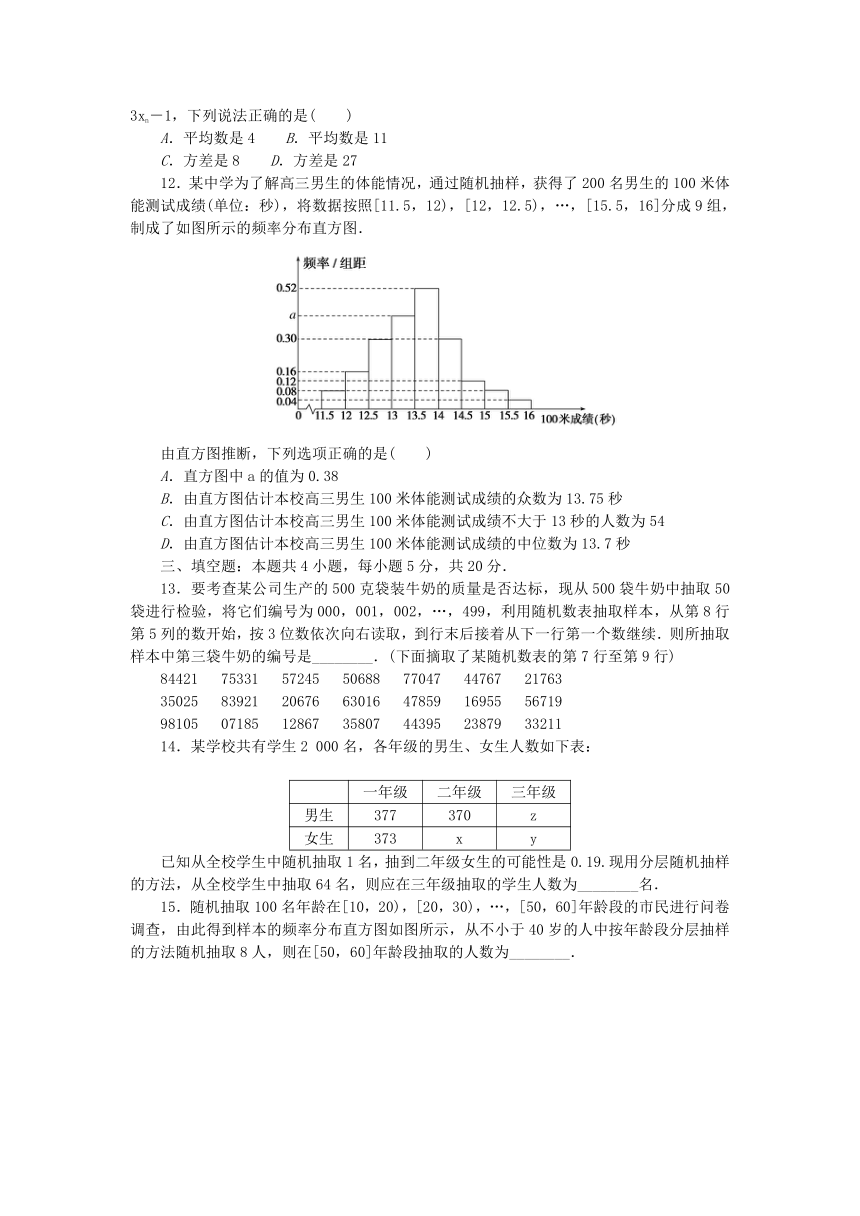
12.某中学为了解高三男生的体能情况,通过随机抽样,获得了200名男生的100米体能测试成绩(单位:秒),将数据按照[11.5,12),[12,12.5),…,[15.5,16]分成9组,制成了如图所示的频率分布直方图.
由直方图推断,下列选项正确的是( )
A.直方图中a的值为0.38
B.由直方图估计本校高三男生100米体能测试成绩的众数为13.75秒
C.由直方图估计本校高三男生100米体能测试成绩不大于13秒的人数为54
D.由直方图估计本校高三男生100米体能测试成绩的中位数为13.7秒
三、填空题:本题共4小题,每小题5分,共20分.
13.要考查某公司生产的500克袋装牛奶的质量是否达标,现从500袋牛奶中抽取50袋进行检验,将它们编号为000,001,002,…,499,利用随机数表抽取样本,从第8行第5列的数开始,按3位数依次向右读取,到行末后接着从下一行第一个数继续.则所抽取样本中第三袋牛奶的编号是________.(下面摘取了某随机数表的第7行至第9行)
84421 75331 57245 50688 77047 44767 21763
35025 83921 20676 63016 47859 16955 56719
98105 07185 12867 35807 44395 23879 33211
14.某学校共有学生2 000名,各年级的男生、女生人数如下表:
一年级 二年级 三年级
男生 377 370 z
女生 373 x y
已知从全校学生中随机抽取1名,抽到二年级女生的可能性是0.19.现用分层随机抽样的方法,从全校学生中抽取64名,则应在三年级抽取的学生人数为________名.
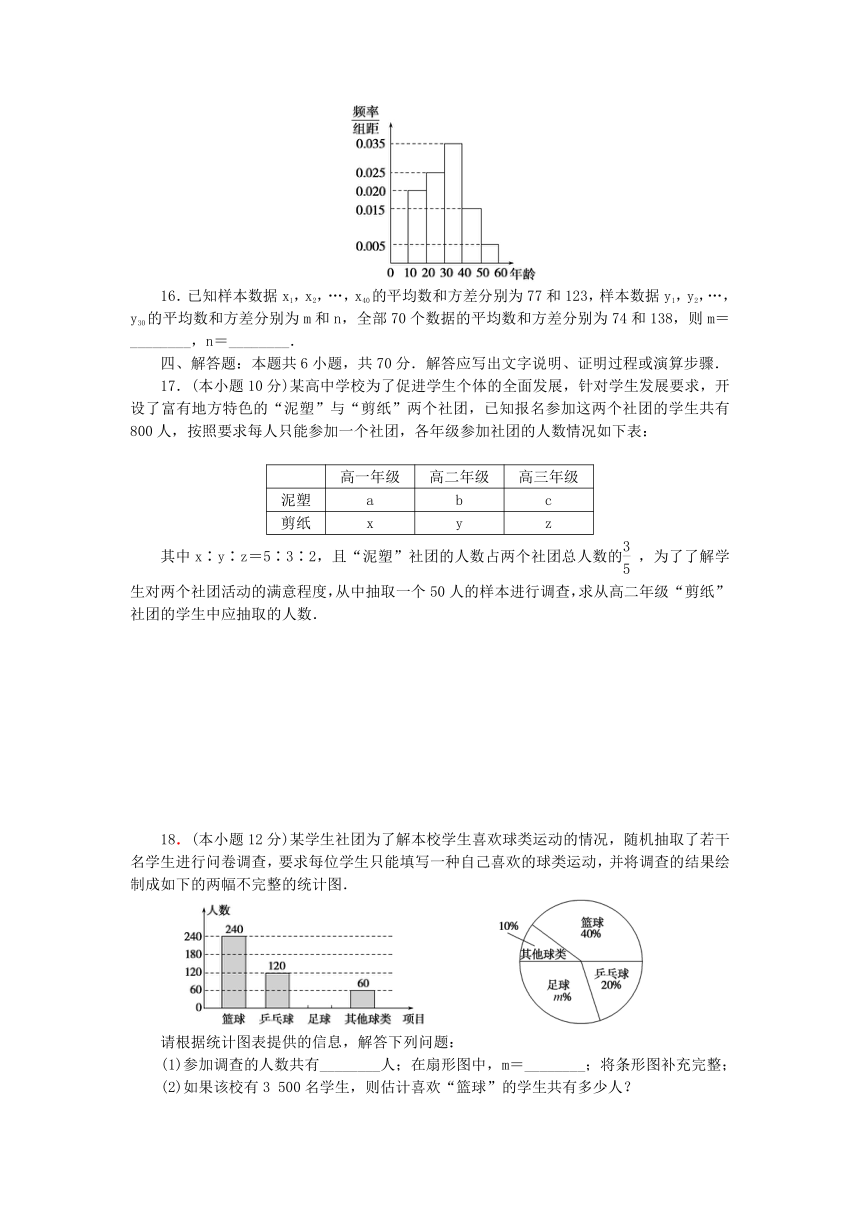
15.随机抽取100名年龄在[10,20),[20,30),…,[50,60]年龄段的市民进行问卷调查,由此得到样本的频率分布直方图如图所示,从不小于40岁的人中按年龄段分层抽样的方法随机抽取8人,则在[50,60]年龄段抽取的人数为________.
16.已知样本数据x1,x2,…,x40的平均数和方差分别为77和123,样本数据y1,y2,…,y30的平均数和方差分别为m和n,全部70个数据的平均数和方差分别为74和138,则m=________,n=________.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题10分)某高中学校为了促进学生个体的全面发展,针对学生发展要求,开设了富有地方特色的“泥塑”与“剪纸”两个社团,已知报名参加这两个社团的学生共有800人,按照要求每人只能参加一个社团,各年级参加社团的人数情况如下表:
高一年级 高二年级 高三年级
泥塑 a b c
剪纸 x y z
其中x∶y∶z=5∶3∶2,且“泥塑”社团的人数占两个社团总人数的,为了了解学生对两个社团活动的满意程度,从中抽取一个50人的样本进行调查,求从高二年级“剪纸”社团的学生中应抽取的人数.
18.(本小题12分)某学生社团为了解本校学生喜欢球类运动的情况,随机抽取了若干名学生进行问卷调查,要求每位学生只能填写一种自己喜欢的球类运动,并将调查的结果绘制成如下的两幅不完整的统计图.
请根据统计图表提供的信息,解答下列问题:
(1)参加调查的人数共有________人;在扇形图中,m=________;将条形图补充完整;
(2)如果该校有3 500名学生,则估计喜欢“篮球”的学生共有多少人?
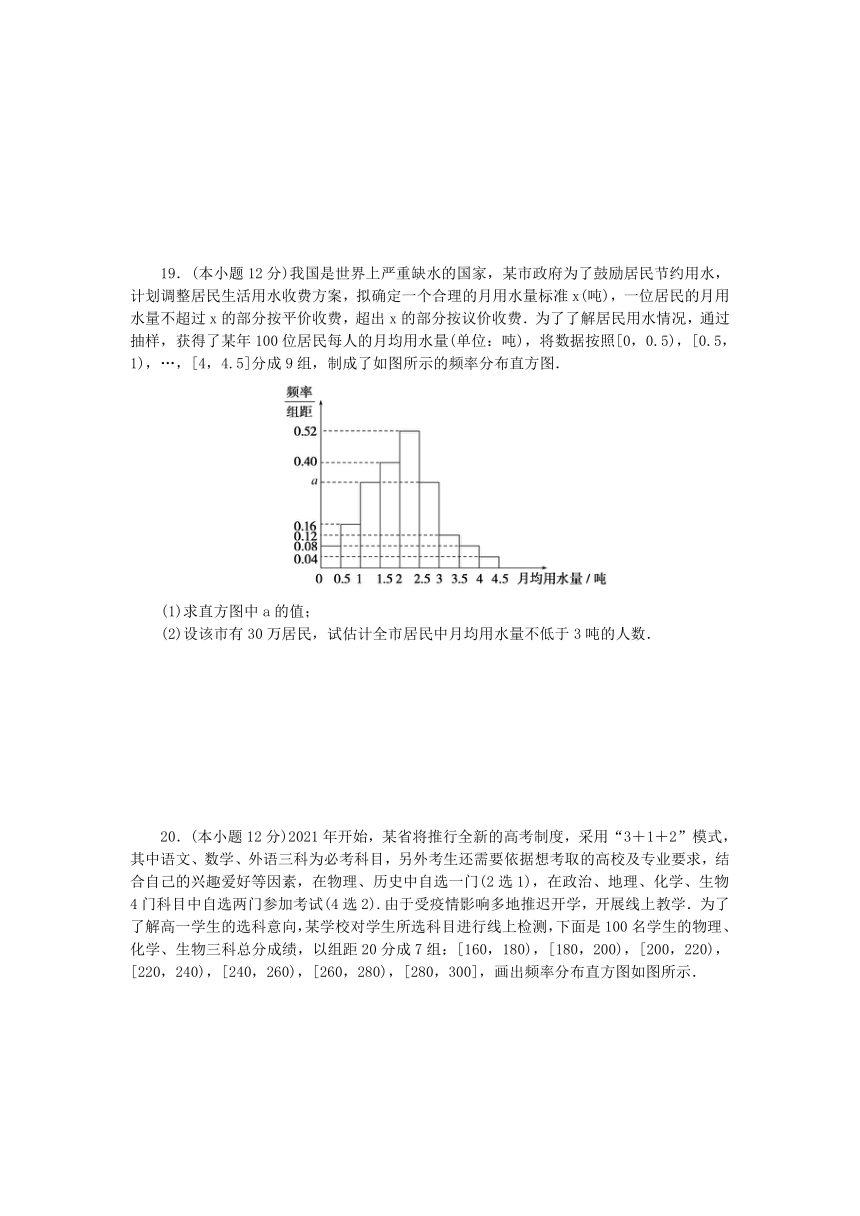
19.(本小题12分)我国是世界上严重缺水的国家,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准x(吨),一位居民的月用水量不超过x的部分按平价收费,超出x的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.
(1)求直方图中a的值;
(2)设该市有30万居民,试估计全市居民中月均用水量不低于3吨的人数.
20.(本小题12分)2021年开始,某省将推行全新的高考制度,采用“3+1+2”模式,其中语文、数学、外语三科为必考科目,另外考生还需要依据想考取的高校及专业要求,结合自己的兴趣爱好等因素,在物理、历史中自选一门(2选1),在政治、地理、化学、生物4门科目中自选两门参加考试(4选2).由于受疫情影响多地推迟开学,开展线上教学.为了了解高一学生的选科意向,某学校对学生所选科目进行线上检测,下面是100名学生的物理、化学、生物三科总分成绩,以组距20分成7组:[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300],画出频率分布直方图如图所示.
(1)求频率分布直方图中a的值;
(2)根据频率分布直方图求物理、化学、生物三科总分成绩的中位数;
(3)估计这100名学生的物理、化学、生物三科总分成绩的平均数.(同一组中的数据用该组区间的中点值作代表)
21.(本小题12分)甲、乙两名跳高运动员进行了8次比赛,他们的成绩(单位:m)如下:
甲:1.70 1.65 1.68 1.69 1.72 1.73 1.68 1.67
乙:1.60 1.73 1.72 1.61 1.62 1.71 1.70 1.75
(1)甲、乙两名运动员的平均跳高成绩分别是多少?
(2)哪位运动员的成绩更为稳定?
(3)教练根据这8次成绩,从甲、乙两名运动员中挑选一个参加省大学生运动会,若预测跳过1.65 m就很可能获得冠军,该校为了获得冠军,可能选哪名运动员参赛?若预测跳过1.70 m才能得冠军呢?
22.(本小题12分)从某校男生中随机抽取100人测量他们的身高,发现他们的身高都在155~185 cm之间,将统计得到的原始数据进行分组,得到如图所示的频率分布直方图(每组均为左闭右开区间).
(1)已知该校一共有1 500名男生,估计该校身高在[165,170)内的男生人数;
(2)估计该校男生身高的90%分位数;(结果精确到0.1)
(3)将身高不低于170 cm的男生称为“高个子”,低于170 cm的男生称为“非高个子”.已知在原始数据中,高个子男生的身高的平均数为177,方差为10,所有这100名男生的身高的平均数为168,方差为64,求非高个子男生的身高的平均数与方差.
单元素养测评卷(四)
1.答案:C
解析:A.了解一批玉米种子的发芽率适合抽样调查,故不符合题意;
B.了解某城市居民的食品消费结构适合抽样调查,故不符合题意;
C.调查一个县各村的粮食播种面积适合全面调查,故符合题意;
D.调查一条河的水质适合抽样调查,故不符合题意.
故选C.
2.答案:C
解析:①的总体中的个体数较少,宜采用简单随机抽样,
②中1 000户家庭中层次比较明显,宜采用分层抽样.
故选C.
3.答案:D
解析:从57开始,每两个数字为一个数依次取出编号为01,02,…,49,50的数为:20,26,31,40,24.所以第5个个体的编号为24.
故选D.
4.答案:A
解析:设这三种型号的零件共抽取的个数为n个,
因为这三种型号的零件周产量之比为2∶3∶5,且抽取的C型号零件25个,
所以n×=25,解得n=50.
所以这三种型号的零件共抽取的个数为50个.
故选A.
5.答案:C
解析:∵10×80%=8,
∴数据6,6,7,7,8,8,8,9,9,10的80%分位数为(9+9)=9.
故选C.
6.答案:B
解析:这五个社团的总人数为=80,=4%.A错误,C错误.
因为太极拳社团人数的占比为×10%=15%,所以脱口秀社团人数的占比为1-10%-15%-30%-25%=20%,B正确.从这五个社团中任选一人,其来自脱口秀社团或舞蹈社团的概率为25%+20%=45%,D错误.
故选B.
7.答案:C
解析:由频率之和为1得10(0.01+0.02+0.03+2a+0.01)=1,
解得a=0.015,
由10×0.01=0.1<0.25,10×0.01+10×0.02=0.3>0.25,
故第25百分位数位于[40,50)内,
则第25百分位数为40+×10=47.5,
可以估计该地区学生每天体育活动时间的第25百分位数约为47.5.
故选C.
8.答案:D
解析:根据中位数的概念,由图可得,A班每天在线学习人数按小到大顺序排列为:22,26,28,34,34,35,38,38,40,中位数34,故A正确;
由图可得,B班每天在线学习人数比A班每天在线学习人数要更稳定,所以,记A班与B班每天在线学习人数的方差分别为s,s,则s>s,故B正确;
根据图象,算出A班与B班每天在线学习人数之和,可知只有22、23、24三天人数和不超过60,C正确;
根据图象,22日到23日不合题意,D结论错误.
故选D.
9.答案:ACD
解析:因为是三种型号的轿车,个体差异明显,所以选择分层随机抽样,所以A正确;
个体数目多,用抽签法制签难,搅拌不均匀,抽出的样本不具有代表性,所以B错误;
因为=,所以1 500×=9(辆),6 000×=36(辆),2 000×=12(辆),所以三种型号的轿车依次应抽取9辆、36辆、12辆,所以C正确;
分层随机抽样中,每一个个体被抽到的可能性相同,故D正确.
故选ACD.
10.答案:ABC
解析:一共有5个分数,从小到大排列,第3个是中位数,依题意可知,中位数是80,
比80大的有85,91两个数,所以0这5个分数的平均值为==65+,
由于0<≤16,所以65<65+≤81,
所以ABC选项符合题意.
故选ABC.
11.答案:BD
解析:设x1,x2,x3,…,xn的平均数为,方差为s2,
则=4,s2=3.
所以3x1-1,3x2-1,…,3xn-1的平均数为3-1=3×4-1=11,方差为32·s2=32×3=27.
故选BD.
12.答案:BC
解析:A:因为频率分布直方图中,所有小矩形的面积之和为1,
所以(0.08+0.16+0.3+a+0.52+0.3+0.12+0.08+0.04)×0.5=1 a=0.4,因此本选项说法不正确;
B:分布在[13.5,14)小组的矩形面积最大,因此众数出现在这个小组内,因此估计众数为=13.75,因此本选项说法正确;
C:高三男生100米体能测试成绩不大于13秒的小组有:[11.5,12),[12,12.5),[12.5,13),频率之和为(0.08+0.16+0.3)×0.5=0.27,因此估计本校高三男生100米体能测试成绩不大于13秒的人数为0.27×200=54,所以本选项说法正确;
D:设中位数为b,因此有(0.08+0.16+0.3+0.4)×0.5+0.52(b-13.5)=0.5 b≈13.56,
所以本选项说法不正确.
故选BC.
13.答案:169
解析:从第8行第5列的数开始向右读,第一个数为583,不符合条件,第二个数为921,不符合条件,第三个数为206,符合条件,以下依次为:766,301,647,859,169,555,其中766,647,859,不符合条件,故第三个数为169.
14.答案:16
解析:由已知抽取的64名学生中一、二年级的学生数为(+0.19)×64=48,
所以三年级的学生数为64-48=16.
15.答案:2
解析:根据频率分布直方图,
得样本中不小于40岁的人的频率是0.015×10+0.005×10=0.2,
所以不小于40岁的人的频数是100×0.2=20;
从不小于40岁的人中按年龄段分层抽样的方法随机抽取8人,
在[50,60]年龄段抽取的人数为8×=8×=2.
16.答案:70 130
解析:由题意,x1+x2+…+x40=40×77,x1+x2+…+x40+y1+y2+…+y30=70×74,故y1+y2+…+y30=70×74-40×77=2 100,故m==70.又(x+x+…+x)-772=123,即x+x+…+x=242 080,(x+x+…+x+y+y+…+y)-742=138,即x+x+…+x+y+y+…+y=392 980,故y+y+…+y=392 980-242 080=150 900,故n=×150 900-702=130.
17.解析:因为“泥塑”社团的人数占总人数的,
故“剪纸”社团的人数占总人数的,
所以“剪纸”社团的人数为800×=320,
因为“剪纸”社团中高二年级人数比例为==,
所以“剪纸”社团中高二年级人数为320×=96,
由题意知,抽样比为=,
所以从高二年级“剪纸”社团中抽取的人数为96×=6.
18.解析:(1)由饼状图可知,喜欢其他球类运动的学生占比10%,由条形图可知喜欢其他球类运动的学生人数为60人,
所以参加调查的人数共60÷10%=600人.
由饼状图可知喜欢足球的学生占比为100%-10%-40%-20%=30%,
所以m=30,
所以,喜欢足球运动的学生人数为600×30%=180人,
所以条形图如图所示:
(2)由饼状图可知,喜欢篮球运动的学生占比40%,
该校有3 500名学生,则估计喜欢“篮球”的学生共有3 500×40%=1 400人.
19.解析:(1)∵0.5×(0.08+0.16+a+0.4+0.52+a+0.12+0.08+0.04)=1,
∴a=0.3.
(2)由图可得月均用水量不低于3吨的频率为0.5×(0.12+0.08+0.04)=0.12,
因为30×0.12=3.6,
∴全市居民中月均用水量不低于3吨的人数约为3.6万.
20.解析:(1)由(0.002+0.009 5+0.011+0.012 5+0.007 5+a+0.002 5)×20=1,得a=0.005.
(2)因为(0.002+0.009 5+0.011)×20=0.45<0.5,(0.002+0.009 5+0.011+0.012 5)×20=0.7>0.5,
所以中位数在[220,240),设中位数为x,
所以(x-220)×0.012 5=0.05,解得x=224,
所以物理、化学、生物三科总分成绩的中位数为224.
(3)这100名学生的物理、化学、生物三科总分成绩的平均数为(0.002×170+0.009 5×190+0.011×210+0.012 5×230+0.007 5×250+0.005×270+0.002 5×290)×20=(0.34+1.805+2.31+2.875+1.875+1.35+0.725)×20=11.28×20=225.6.
21.解析:(1)甲的平均成绩为(1.70+1.65+1.68+1.69+1.72+1.73+1.68+1.67)÷8=1.69(m).
乙的平均成绩为(1.60+1.73+1.72+1.61+1.62+1.71+1.70+1.75)÷8=1.68(m).
(2)s=×[(1.70-1.69)2+(1.65-1.69)2+…+(1.67-1.69)2]=0.000 6.
s=×[(1.60-1.68)2+(1.73-1.68)2+…+(1.75-1.68)2]=0.003 15.
显然,甲的平均成绩好于乙的平均成绩,而且甲的方差小于乙的方差,说明甲的成绩比乙稳定.
(3)由于甲的平均成绩高于乙,且成绩稳定,且甲1.65 m以上的成绩有8次,乙1.65 m以上的成绩有5次,所以若跳过1.65 m就很可能获得冠军,应派甲参赛.
由于甲1.70 m以上的成绩有3次,乙1.70 m以上的成绩有5次,所以若跳过1.70 m才能获得冠军,应派乙参赛.
22.解析:(1)由频率分布直方图可知(0.024+0.036+x+0.044+0.024+0.012)×5=1,
得x=0.06.
故估计该校1 500名男生中身高在[165,170)内的人数为1 500×0.06×5=450.
(2)前四组的频率之和为(0.024+0.036+0.06+0.044)×5=0.82<0.9,
前五组的频率之和为0.82+0.024×5=0.94>0.9,所以90%分位数位于区间[175,180)内,
故估计该校男生身高的90%分位数为175+×5≈178.3.
(3)由频率分布直方图可知,样本中高个子男生有40人,非高个子男生有60人.
将高个子男生的身高数据记为x1,x2,…,x40,其平均数记为,方差记为s;将非高个子男生的身高数据记为y1,y2,…,y60,其平均数记为,方差记为s;把全部样本数据的平均数记为,方差记为s2.
则=177,s=10,=168,s2=64.
由已知可得=+,即168=177×0.4+0.6,得=162,
s2=[(xi-)2+(yi-)2]=[s+(-)2]+[s+(-)2].
所以64=0.4×(10+92)+0.6×(s+62),解得s=10.
综上所述,非高个子男生的身高的平均数为162,方差为10.
时间:120分钟 满分:150分
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.下列情况适合用全面调查的是( )
A.了解一批玉米种子的发芽率
B.了解某城市居民的食品消费结构
C.调查一个县各村的粮食播种面积
D.调查一条河的水质
2.现有以下两项调查:①从100台刚出厂的电视机中抽取3台进行质量检查;②某社区有1 000户家庭,其中高收入家庭100户,中等收入家庭820户,低收入家庭80户,为了调查家庭每年生活费的开支情况,计划抽取一个容量为50的样本,则完成这两项调查最适宜采用的抽样方法分别是( )
A.①②都采用简单随机抽样
B.①②都采用分层随机抽样
C.①采用简单随机抽样,②采用分层随机抽样
D.①采用分层随机抽样,②采用简单随机抽样
3.现利用随机数法从高一(3)班的50名同学中选取5名同学参与学校活动.该班同学分别编号为01,02,…,49,50.选取方法是从随机数表第1行第6列的数开始由左到右依次选取两个数字,则选出来的第5个个体的编号为( )
(注:下表为随机数表的第1行和第2行)
7816 6572 0802 6314 0702 4369 9728 0198
3204 9243 4935 8200 3623 4869 6938 7481
A.31 B.40 C.36 D.24
4.已知某工厂生产A,B,C三种型号的零件,这三种型号的零件周产量之比为2∶3∶5,现在用分层抽样的方法从某周生产的零件中抽取若干个进行质量检查,若抽取C型号零件25个,则这三种型号的零件共抽取的个数为( )
A.50 B.55 C.60 D.65
5.幸福感指数是指某个人主观评价他对自己目前生活状态满意程度的指标,常用区间[0,10]内的一个数来表示,该数越接近10表示满意度越高.现随机抽取10位市民,他们的幸福感指数分别为6,6,7,7,8,8,8,9,9,10,则这组数据的80%分位数是( )
A.8 B.8.5 C.9 D.9.5
6.
某学校组建了合唱、朗诵、脱口秀、舞蹈、太极拳五个社团,该校共有2 000名同学,每名同学依据自己的兴趣爱好最多可参加其中一个,各个社团的人数比例的饼状图如图所示,其中参加朗诵社团的同学有8名,参加太极拳社团的有12名,则( )
A.这五个社团的总人数为100
B.脱口秀社团的人数占五个社团总人数的20%
C.这五个社团总人数占该校学生人数的8%
D.从这五个社团中任选一人,其来自脱口秀社团或舞蹈社团的概率为50%
7.为了解“双减”政策实施后学生每天的体育活动时间,研究人员随机调查了该地区1 000名学生每天进行体育运动的时间,按照时长(单位:分钟)分成6组:第一组[30,40),第二组[40,50),第三组[50,60),第四组[60,70),第五组[70,80),第六组[80,90],经整理得到如图的频率分布直方图,则可以估计该地区学生每天体育活动时间的第25百分位数约为( )
A.42.5分钟 B.45.5分钟 C.47.5分钟 D.50分钟
8.疫情期间,某校为了了解学生在线学习情况,统计了该校A,B两班2022年2月18日~2月26日每天在线学习人数情况,如图所示:
下列说法不正确的是( )
A.A班每天在线学习人数的中位数为34
B.记A班与B班每天在线学习人数的方差分别为s,s,则s>s
C.A班与B班每天在线学习人数之和不超过60的天数为3天
D.从20日~23日,A班与B班每天在线学习人数都在逐日减少
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.某公司生产三种型号的轿车,年产量分别为1 500辆、6 000辆和2 000辆.为检验产品质量,公司质检部门要抽取57辆进行检验,则下列说法正确的是( )
A.应采用分层随机抽样抽取
B.应采用抽签法抽取
C.三种型号的轿车依次应抽取9辆、36辆、12辆
D.这三种型号的轿车,每一辆被抽到的可能性相同
10.某学生5次考试的成绩(单位:分)分别为85,69,m,80,91,其中m>0.若该学生在这5次考试中成绩的中位数为80,则5次考试成绩的平均数可能为( )
A.76 B.80 C.81 D.85
11.一组数据x1,x2,…,xn的平均数是4,方差为3,关于数据3x1-1,3x2-1,…,3xn-1,下列说法正确的是( )
A.平均数是4 B.平均数是11
C.方差是8 D.方差是27
12.某中学为了解高三男生的体能情况,通过随机抽样,获得了200名男生的100米体能测试成绩(单位:秒),将数据按照[11.5,12),[12,12.5),…,[15.5,16]分成9组,制成了如图所示的频率分布直方图.
由直方图推断,下列选项正确的是( )
A.直方图中a的值为0.38
B.由直方图估计本校高三男生100米体能测试成绩的众数为13.75秒
C.由直方图估计本校高三男生100米体能测试成绩不大于13秒的人数为54
D.由直方图估计本校高三男生100米体能测试成绩的中位数为13.7秒
三、填空题:本题共4小题,每小题5分,共20分.
13.要考查某公司生产的500克袋装牛奶的质量是否达标,现从500袋牛奶中抽取50袋进行检验,将它们编号为000,001,002,…,499,利用随机数表抽取样本,从第8行第5列的数开始,按3位数依次向右读取,到行末后接着从下一行第一个数继续.则所抽取样本中第三袋牛奶的编号是________.(下面摘取了某随机数表的第7行至第9行)
84421 75331 57245 50688 77047 44767 21763
35025 83921 20676 63016 47859 16955 56719
98105 07185 12867 35807 44395 23879 33211
14.某学校共有学生2 000名,各年级的男生、女生人数如下表:
一年级 二年级 三年级
男生 377 370 z
女生 373 x y
已知从全校学生中随机抽取1名,抽到二年级女生的可能性是0.19.现用分层随机抽样的方法,从全校学生中抽取64名,则应在三年级抽取的学生人数为________名.
15.随机抽取100名年龄在[10,20),[20,30),…,[50,60]年龄段的市民进行问卷调查,由此得到样本的频率分布直方图如图所示,从不小于40岁的人中按年龄段分层抽样的方法随机抽取8人,则在[50,60]年龄段抽取的人数为________.
16.已知样本数据x1,x2,…,x40的平均数和方差分别为77和123,样本数据y1,y2,…,y30的平均数和方差分别为m和n,全部70个数据的平均数和方差分别为74和138,则m=________,n=________.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题10分)某高中学校为了促进学生个体的全面发展,针对学生发展要求,开设了富有地方特色的“泥塑”与“剪纸”两个社团,已知报名参加这两个社团的学生共有800人,按照要求每人只能参加一个社团,各年级参加社团的人数情况如下表:
高一年级 高二年级 高三年级
泥塑 a b c
剪纸 x y z
其中x∶y∶z=5∶3∶2,且“泥塑”社团的人数占两个社团总人数的,为了了解学生对两个社团活动的满意程度,从中抽取一个50人的样本进行调查,求从高二年级“剪纸”社团的学生中应抽取的人数.
18.(本小题12分)某学生社团为了解本校学生喜欢球类运动的情况,随机抽取了若干名学生进行问卷调查,要求每位学生只能填写一种自己喜欢的球类运动,并将调查的结果绘制成如下的两幅不完整的统计图.
请根据统计图表提供的信息,解答下列问题:
(1)参加调查的人数共有________人;在扇形图中,m=________;将条形图补充完整;
(2)如果该校有3 500名学生,则估计喜欢“篮球”的学生共有多少人?
19.(本小题12分)我国是世界上严重缺水的国家,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准x(吨),一位居民的月用水量不超过x的部分按平价收费,超出x的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.
(1)求直方图中a的值;
(2)设该市有30万居民,试估计全市居民中月均用水量不低于3吨的人数.
20.(本小题12分)2021年开始,某省将推行全新的高考制度,采用“3+1+2”模式,其中语文、数学、外语三科为必考科目,另外考生还需要依据想考取的高校及专业要求,结合自己的兴趣爱好等因素,在物理、历史中自选一门(2选1),在政治、地理、化学、生物4门科目中自选两门参加考试(4选2).由于受疫情影响多地推迟开学,开展线上教学.为了了解高一学生的选科意向,某学校对学生所选科目进行线上检测,下面是100名学生的物理、化学、生物三科总分成绩,以组距20分成7组:[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300],画出频率分布直方图如图所示.
(1)求频率分布直方图中a的值;
(2)根据频率分布直方图求物理、化学、生物三科总分成绩的中位数;
(3)估计这100名学生的物理、化学、生物三科总分成绩的平均数.(同一组中的数据用该组区间的中点值作代表)
21.(本小题12分)甲、乙两名跳高运动员进行了8次比赛,他们的成绩(单位:m)如下:
甲:1.70 1.65 1.68 1.69 1.72 1.73 1.68 1.67
乙:1.60 1.73 1.72 1.61 1.62 1.71 1.70 1.75
(1)甲、乙两名运动员的平均跳高成绩分别是多少?
(2)哪位运动员的成绩更为稳定?
(3)教练根据这8次成绩,从甲、乙两名运动员中挑选一个参加省大学生运动会,若预测跳过1.65 m就很可能获得冠军,该校为了获得冠军,可能选哪名运动员参赛?若预测跳过1.70 m才能得冠军呢?
22.(本小题12分)从某校男生中随机抽取100人测量他们的身高,发现他们的身高都在155~185 cm之间,将统计得到的原始数据进行分组,得到如图所示的频率分布直方图(每组均为左闭右开区间).
(1)已知该校一共有1 500名男生,估计该校身高在[165,170)内的男生人数;
(2)估计该校男生身高的90%分位数;(结果精确到0.1)
(3)将身高不低于170 cm的男生称为“高个子”,低于170 cm的男生称为“非高个子”.已知在原始数据中,高个子男生的身高的平均数为177,方差为10,所有这100名男生的身高的平均数为168,方差为64,求非高个子男生的身高的平均数与方差.
单元素养测评卷(四)
1.答案:C
解析:A.了解一批玉米种子的发芽率适合抽样调查,故不符合题意;
B.了解某城市居民的食品消费结构适合抽样调查,故不符合题意;
C.调查一个县各村的粮食播种面积适合全面调查,故符合题意;
D.调查一条河的水质适合抽样调查,故不符合题意.
故选C.
2.答案:C
解析:①的总体中的个体数较少,宜采用简单随机抽样,
②中1 000户家庭中层次比较明显,宜采用分层抽样.
故选C.
3.答案:D
解析:从57开始,每两个数字为一个数依次取出编号为01,02,…,49,50的数为:20,26,31,40,24.所以第5个个体的编号为24.
故选D.
4.答案:A
解析:设这三种型号的零件共抽取的个数为n个,
因为这三种型号的零件周产量之比为2∶3∶5,且抽取的C型号零件25个,
所以n×=25,解得n=50.
所以这三种型号的零件共抽取的个数为50个.
故选A.
5.答案:C
解析:∵10×80%=8,
∴数据6,6,7,7,8,8,8,9,9,10的80%分位数为(9+9)=9.
故选C.
6.答案:B
解析:这五个社团的总人数为=80,=4%.A错误,C错误.
因为太极拳社团人数的占比为×10%=15%,所以脱口秀社团人数的占比为1-10%-15%-30%-25%=20%,B正确.从这五个社团中任选一人,其来自脱口秀社团或舞蹈社团的概率为25%+20%=45%,D错误.
故选B.
7.答案:C
解析:由频率之和为1得10(0.01+0.02+0.03+2a+0.01)=1,
解得a=0.015,
由10×0.01=0.1<0.25,10×0.01+10×0.02=0.3>0.25,
故第25百分位数位于[40,50)内,
则第25百分位数为40+×10=47.5,
可以估计该地区学生每天体育活动时间的第25百分位数约为47.5.
故选C.
8.答案:D
解析:根据中位数的概念,由图可得,A班每天在线学习人数按小到大顺序排列为:22,26,28,34,34,35,38,38,40,中位数34,故A正确;
由图可得,B班每天在线学习人数比A班每天在线学习人数要更稳定,所以,记A班与B班每天在线学习人数的方差分别为s,s,则s>s,故B正确;
根据图象,算出A班与B班每天在线学习人数之和,可知只有22、23、24三天人数和不超过60,C正确;
根据图象,22日到23日不合题意,D结论错误.
故选D.
9.答案:ACD
解析:因为是三种型号的轿车,个体差异明显,所以选择分层随机抽样,所以A正确;
个体数目多,用抽签法制签难,搅拌不均匀,抽出的样本不具有代表性,所以B错误;
因为=,所以1 500×=9(辆),6 000×=36(辆),2 000×=12(辆),所以三种型号的轿车依次应抽取9辆、36辆、12辆,所以C正确;
分层随机抽样中,每一个个体被抽到的可能性相同,故D正确.
故选ACD.
10.答案:ABC
解析:一共有5个分数,从小到大排列,第3个是中位数,依题意可知,中位数是80,
比80大的有85,91两个数,所以0
由于0<≤16,所以65<65+≤81,
所以ABC选项符合题意.
故选ABC.
11.答案:BD
解析:设x1,x2,x3,…,xn的平均数为,方差为s2,
则=4,s2=3.
所以3x1-1,3x2-1,…,3xn-1的平均数为3-1=3×4-1=11,方差为32·s2=32×3=27.
故选BD.
12.答案:BC
解析:A:因为频率分布直方图中,所有小矩形的面积之和为1,
所以(0.08+0.16+0.3+a+0.52+0.3+0.12+0.08+0.04)×0.5=1 a=0.4,因此本选项说法不正确;
B:分布在[13.5,14)小组的矩形面积最大,因此众数出现在这个小组内,因此估计众数为=13.75,因此本选项说法正确;
C:高三男生100米体能测试成绩不大于13秒的小组有:[11.5,12),[12,12.5),[12.5,13),频率之和为(0.08+0.16+0.3)×0.5=0.27,因此估计本校高三男生100米体能测试成绩不大于13秒的人数为0.27×200=54,所以本选项说法正确;
D:设中位数为b,因此有(0.08+0.16+0.3+0.4)×0.5+0.52(b-13.5)=0.5 b≈13.56,
所以本选项说法不正确.
故选BC.
13.答案:169
解析:从第8行第5列的数开始向右读,第一个数为583,不符合条件,第二个数为921,不符合条件,第三个数为206,符合条件,以下依次为:766,301,647,859,169,555,其中766,647,859,不符合条件,故第三个数为169.
14.答案:16
解析:由已知抽取的64名学生中一、二年级的学生数为(+0.19)×64=48,
所以三年级的学生数为64-48=16.
15.答案:2
解析:根据频率分布直方图,
得样本中不小于40岁的人的频率是0.015×10+0.005×10=0.2,
所以不小于40岁的人的频数是100×0.2=20;
从不小于40岁的人中按年龄段分层抽样的方法随机抽取8人,
在[50,60]年龄段抽取的人数为8×=8×=2.
16.答案:70 130
解析:由题意,x1+x2+…+x40=40×77,x1+x2+…+x40+y1+y2+…+y30=70×74,故y1+y2+…+y30=70×74-40×77=2 100,故m==70.又(x+x+…+x)-772=123,即x+x+…+x=242 080,(x+x+…+x+y+y+…+y)-742=138,即x+x+…+x+y+y+…+y=392 980,故y+y+…+y=392 980-242 080=150 900,故n=×150 900-702=130.
17.解析:因为“泥塑”社团的人数占总人数的,
故“剪纸”社团的人数占总人数的,
所以“剪纸”社团的人数为800×=320,
因为“剪纸”社团中高二年级人数比例为==,
所以“剪纸”社团中高二年级人数为320×=96,
由题意知,抽样比为=,
所以从高二年级“剪纸”社团中抽取的人数为96×=6.
18.解析:(1)由饼状图可知,喜欢其他球类运动的学生占比10%,由条形图可知喜欢其他球类运动的学生人数为60人,
所以参加调查的人数共60÷10%=600人.
由饼状图可知喜欢足球的学生占比为100%-10%-40%-20%=30%,
所以m=30,
所以,喜欢足球运动的学生人数为600×30%=180人,
所以条形图如图所示:
(2)由饼状图可知,喜欢篮球运动的学生占比40%,
该校有3 500名学生,则估计喜欢“篮球”的学生共有3 500×40%=1 400人.
19.解析:(1)∵0.5×(0.08+0.16+a+0.4+0.52+a+0.12+0.08+0.04)=1,
∴a=0.3.
(2)由图可得月均用水量不低于3吨的频率为0.5×(0.12+0.08+0.04)=0.12,
因为30×0.12=3.6,
∴全市居民中月均用水量不低于3吨的人数约为3.6万.
20.解析:(1)由(0.002+0.009 5+0.011+0.012 5+0.007 5+a+0.002 5)×20=1,得a=0.005.
(2)因为(0.002+0.009 5+0.011)×20=0.45<0.5,(0.002+0.009 5+0.011+0.012 5)×20=0.7>0.5,
所以中位数在[220,240),设中位数为x,
所以(x-220)×0.012 5=0.05,解得x=224,
所以物理、化学、生物三科总分成绩的中位数为224.
(3)这100名学生的物理、化学、生物三科总分成绩的平均数为(0.002×170+0.009 5×190+0.011×210+0.012 5×230+0.007 5×250+0.005×270+0.002 5×290)×20=(0.34+1.805+2.31+2.875+1.875+1.35+0.725)×20=11.28×20=225.6.
21.解析:(1)甲的平均成绩为(1.70+1.65+1.68+1.69+1.72+1.73+1.68+1.67)÷8=1.69(m).
乙的平均成绩为(1.60+1.73+1.72+1.61+1.62+1.71+1.70+1.75)÷8=1.68(m).
(2)s=×[(1.70-1.69)2+(1.65-1.69)2+…+(1.67-1.69)2]=0.000 6.
s=×[(1.60-1.68)2+(1.73-1.68)2+…+(1.75-1.68)2]=0.003 15.
显然,甲的平均成绩好于乙的平均成绩,而且甲的方差小于乙的方差,说明甲的成绩比乙稳定.
(3)由于甲的平均成绩高于乙,且成绩稳定,且甲1.65 m以上的成绩有8次,乙1.65 m以上的成绩有5次,所以若跳过1.65 m就很可能获得冠军,应派甲参赛.
由于甲1.70 m以上的成绩有3次,乙1.70 m以上的成绩有5次,所以若跳过1.70 m才能获得冠军,应派乙参赛.
22.解析:(1)由频率分布直方图可知(0.024+0.036+x+0.044+0.024+0.012)×5=1,
得x=0.06.
故估计该校1 500名男生中身高在[165,170)内的人数为1 500×0.06×5=450.
(2)前四组的频率之和为(0.024+0.036+0.06+0.044)×5=0.82<0.9,
前五组的频率之和为0.82+0.024×5=0.94>0.9,所以90%分位数位于区间[175,180)内,
故估计该校男生身高的90%分位数为175+×5≈178.3.
(3)由频率分布直方图可知,样本中高个子男生有40人,非高个子男生有60人.
将高个子男生的身高数据记为x1,x2,…,x40,其平均数记为,方差记为s;将非高个子男生的身高数据记为y1,y2,…,y60,其平均数记为,方差记为s;把全部样本数据的平均数记为,方差记为s2.
则=177,s=10,=168,s2=64.
由已知可得=+,即168=177×0.4+0.6,得=162,
s2=[(xi-)2+(yi-)2]=[s+(-)2]+[s+(-)2].
所以64=0.4×(10+92)+0.6×(s+62),解得s=10.
综上所述,非高个子男生的身高的平均数为162,方差为10.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
