1.4.1用空间向量研究直线平面的位置关系 课时作业(含解析)
文档属性
| 名称 | 1.4.1用空间向量研究直线平面的位置关系 课时作业(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 336.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-11 00:00:00 | ||
图片预览




文档简介
1.4.1 用空间向量研究直线、平面的位置关系
必备知识基础练 进阶训练第一层
1.已知平面α外的直线l的方向向量是a=(3,2,1),平面α的法向量是u=(-1,2,-1),则l与α的位置关系是( )
A.l⊥α B.l∥α
C.l与α相交但不垂直 D.l∥α或l α
2.已知直线l的方向向量为a=(1,1,2),平面α的法向量为n=(2,2,4),则( )
A.l∥α B.l⊥α
C.l α D.l与α相交
3.[2023·山西大同高二检测]已知平面α和平面β的法向量分别为m=(3,1,-5),n=(-6,-2,10),则( )
A.α⊥β
B.α∥β
C.α与β相交但不垂直
D.以上都不对
4.[2023·安徽宿州高二检测]若向量a=(1,1,-1)是直线l的一个方向向量,n=(-1,2,2)是平面α的一个法向量,则直线l与平面α的位置关系是( )
A.平行 B.垂直
C.直线l在平面α内 D.相交但不垂直
5.已知A(1,0,0),B(0,1,0),C(0,0,1),则下列向量是平面ABC法向量的是( )
A.(-1,1,1) B.(1,1,1)
C.(-,,-) D.(,,-)
6.(多选)若v为直线l的方向向量,m,n分别为平面α,β的法向量(α,β不重合),则下列说法正确的有( )
A.v∥m l∥α B.v⊥m l⊥α
C.m∥n α∥β D.m⊥n α⊥β
7.法向量分别是n=(1,-1,2),m=(-2,0,3)的两个平面的位置关系是________________.
8.[2023·北京北师大附中高二检测]已知A(1,0,0),B(0,2,0),C(0,0,3),则平面ABC的一个法向量的坐标为________.
关键能力综合练 进阶训练第二层
1.已知u是直线l的方向向量,n是平面α的法向量,则“l α”是“u⊥n”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
2.已知向量=(2,4,x),平面α的一个法向量n=(1,y,3),若AB∥α,则( )
A.x=6,y=2
B.x=2,y=6
C.3x+4y+2=0
D.4x+3y+2=0
3.已知平面α的法向量为(2,-4,-2),平面β的法向量为(-1,2,k),若α∥β,则k=( )
A.-2 B.-1
C.1 D.2
4.[2023·福建泉州高二检测]已知点A(2,-1,2)在平面α内,n=(3,1,2)是平面α的一个法向量,则下列各点在平面α内的是( )
A.(1,-1,1) B.(1,3,)
C.(1,-3,) D.(-1,3,-)
5.[2023·山东青岛高二检测]已知直线l和平面ABC,若直线l的方向向量为n=(1,-2,-5),向量=(1,0,-1),=(2,1,0),则下列结论一定正确的为( )
A.l⊥平面ABC
B.l与平面ABC相交,但不垂直
C.l∥直线BC
D.l∥平面ABC或l 平面ABC
6.[2023·福建厦门高二测试](多选)如图,直三棱柱ABC A1B1C1中,CA⊥CB,CA=CB=CC1,D,E,M分别为B1C1,CC1,AB1的中点,点N是棱AC上一动点,则( )
A.MN⊥BC1
B.存在点N,使MN⊥平面BC1N
C.MN∥平面A1DE
D.存在点N,使MN∥DE
7.已知向量a=(1-m,1,m)是直线l的一个方向向量,向量n=(-2,m,1)是平面α的一个法向量,若直线l⊥平面α,则实数m的值为________.
8.在长方体ABCD A1B1C1D1中,AB=2,BC=CC1=1,若在CD上存在点E,使得A1E⊥平面AB1D1,则DE=________.
9.[2023·广东江门高二测试]如图,在棱长为3的正方体ABCD A1B1C1D1中,点M在棱C1C上,且CM=2MC1.以D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系.
(1)求平面ABB1A1的一个法向量;
(2)求平面MD1B的一个法向量.
10.
在直三棱柱ABC A1B1C1中,∠ABC=90°,BC=2,CC1=4,点E在线段BB1上,且EB1=1,D,F,G分别为CC1,C1B1,C1A1的中点.
(1)证明:B1D⊥平面ABD;
(2)证明:平面EGF∥平面ABD.
核心素养升级练 进阶训练第三层
1.
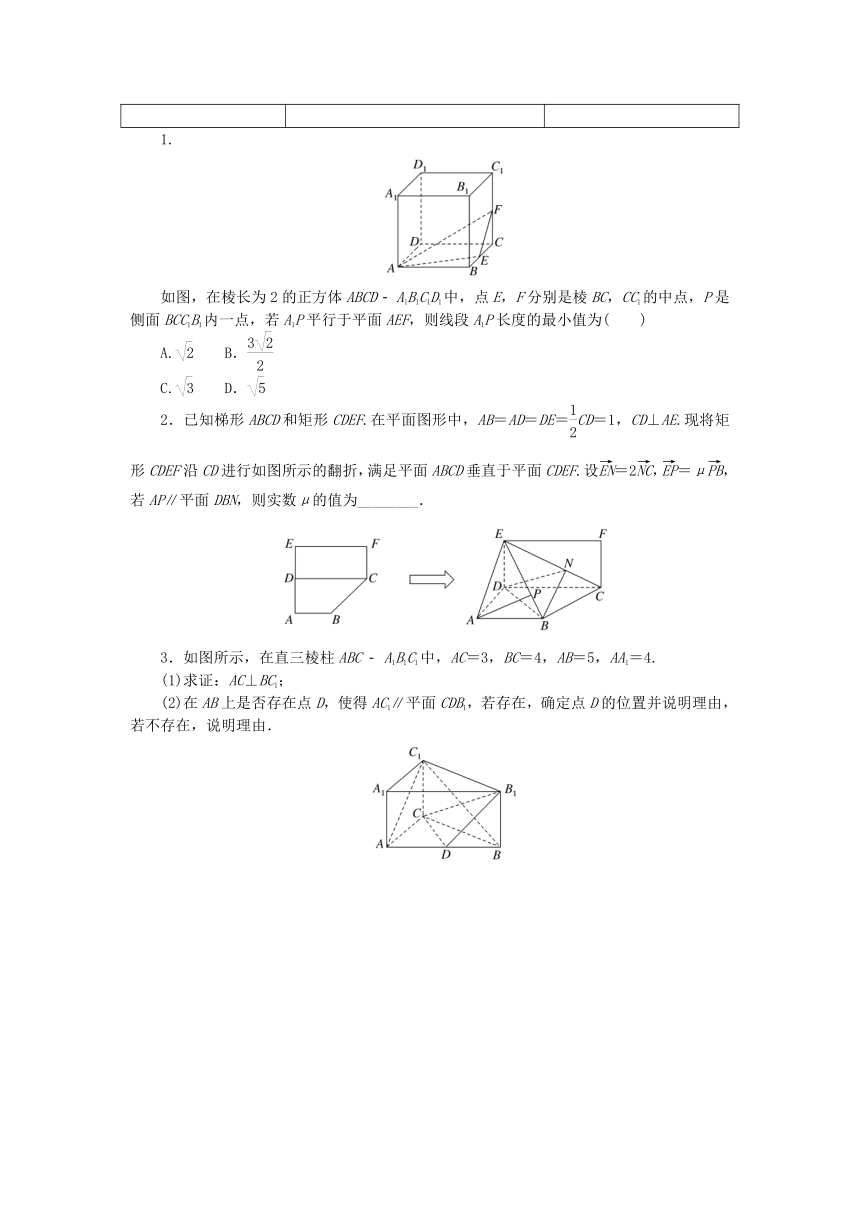
如图,在棱长为2的正方体ABCD A1B1C1D1中,点E,F分别是棱BC,CC1的中点,P是侧面BCC1B1内一点,若A1P平行于平面AEF,则线段A1P长度的最小值为( )
A. B.
C. D.
2.已知梯形ABCD和矩形CDEF.在平面图形中,AB=AD=DE=CD=1,CD⊥AE.现将矩形CDEF沿CD进行如图所示的翻折,满足平面ABCD垂直于平面CDEF.设=2,=μ,若AP∥平面DBN,则实数μ的值为________.
3.如图所示,在直三棱柱ABC A1B1C1中,AC=3,BC=4,AB=5,AA1=4.
(1)求证:AC⊥BC1;
(2)在AB上是否存在点D,使得AC1∥平面CDB1,若存在,确定点D的位置并说明理由,若不存在,说明理由.
1.4.1 用空间向量研究直线、平面的位置关系
必备知识基础练
1.答案:B
解析:由于a·u=(3,2,1)·(-1,2,-1)=-3+4-1=0,即a⊥u,由于l α,所以l∥α.故选B.
2.答案:B
解析:因为n=(2,2,4),a=(1,1,2),故可得n=2a,即n∥a,则直线l⊥α.故选B.
3.答案:B
解析:∵m=(3,1,-5),n=(-6,-2,10),∴n=-2m,
∴m∥n,∴α∥β.故选B.
4.答案:D
解析:a=(1,1,-1),n=(-1,2,2),a·n=-1+2-2=-1≠0,故a与n不垂直,即直线l与平面α不平行;若n=λa,则(-1,2,2)=λ(1,1,-1),无解,故a与n不平行,即直线l与平面α不垂直.故选D.
5.答案:B
解析:由题意,得=(-1,1,0),=(-1,0,1),设n=(x,y,z)为平面ABC的法向量,则,化简得,∴x=y=z.令x=1,有n=(1,1,1).故选B.
6.答案:CD
解析:对于A,v∥m l⊥α,错误;对于B,v⊥m l∥α或l α,错误;对于C,α,β不重合,m∥n α∥β,正确;对于D,m⊥n α⊥β,正确.故选CD.
7.答案:相交且不垂直
解析:假设存在λ∈R,使得n=λm,则,显然方程组无解,所以n,m不平行,即两个平面不平行;因为n·m=-2+6=4≠0,所以n与m不垂直,所以两个平面的位置关系是相交且不垂直.
8.答案:(6,3,2)(答案不唯一)
解析:因为A(1,0,0),B(0,2,0),C(0,0,3),所以=(-1,2,0),=(-1,0,3),设平面ABC的法向量为n=(x,y,z),则,即,令x=6,则y=3,z=2,所以n=(6,3,2).
关键能力综合练
1.答案:A
解析:已知u是直线l的方向向量,n是平面α的法向量,则u⊥n等价于l∥α或l α,所以“l α”是“u⊥n”的充分不必要条件.故选A.
2.答案:C
解析:因为AB∥α,则⊥n,则·n=2+4y+3x=0,故选C.
3.答案:C
解析:设平面α,平面β的法向量分别用m,n表示,由题意得m=(2,-4,-2)与n=(-1,2,k)平行,故m=tn,即,解得.故选C.
4.答案:B
解析:设平面α内的一点为P(x,y,z)(不与点A重合),则=(x-2,y+1,z-2),因为n=(3,1,2)是平面α的一个法向量,所以⊥n,所以·n=3(x-2)+(y+1)+2(z-2)=0,即3x+y+2z=9,对于A:3×1+(-1)+2×1=4≠9,故选项A不正确;对于B:3×1+3+2×=9,故选项B正确;对于C:3×1+(-3)+2×=3≠9,故选项C不正确;对于D:3×(-1)+3+2×=-3≠9,故选项D不正确.故选B.
5.答案:D
解析:n·=1+0+5=6≠0,n与不垂直,也即l与AB不垂直,所以直线l与平面α不垂直,A错;=-=(1,1,1),因此不存在实数k,使得n=k,所以n与不平行,即直线l与直线BC不平行,C错;设m=(x,y,z)是平面ABC的一个法向量,则,取x=1,则m=(1,-2,1),m·n=1+4-5=0,所以m⊥n,所以直线l与平面ABC平行或在平面ABC内,B错,D正确.故选D.
6.答案:AD
解析:A选项:连接BC1,B1C,由题可知四边形BCC1B1是正方形,则BC1⊥B1C,由题知平面BCC1B1⊥平面ABC,平面BCC1B1∩平面ABC=BC,AC⊥BC,AC 平面ABC,∴AC⊥平面BCC1B1,又BC1 平面BCC1B1,∴AC⊥BC1,又B1C∩AC=C,B1C,AC 平面AB1C,∴BC1⊥平面AB1C,∵MN 平面AB1C,∴BC1⊥MN.故A正确;
B选项:如图建立空间直角坐标系,设AC=BC=CC1=2,则C(0,0,0),B(2,0,0),A(0,2,0),B1(2,0,2),M(1,1,1),设N(0,t,0),0C选项:当N是AC中点时,MN∥B1C,B1C∥DE,∴MN∥平面A1DE;当N不是AC中点时,MN和B1C相交,若MN∥平面A1DE,结合B1C∥平面A1DE可知平面AB1C∥平面A1DE,这显然与图形不符(A1E与AC相交),故此时MN与平面A1DE不平行,故C错误;
D选项:由C项可知,N为AC中点满足题意,故D正确.
故选AD.
7.答案:-1
解析:因为直线l⊥平面α,则a=(1-m,1,m)与n=(-2,m,1)平行,故a=λn,即,解得m=-1,故实数m的值为-1.
8.答案:
解析:因为ABCD A1B1C1D1,所以DA,DC,DD1两两垂直,建立如图所示坐标系:
设DE=t,所以A1(1,0,1),E(0,t,0),A(1,0,0),B1(1,2,1),D1(0,0,1),则=(-1,t,-1),=(0,2,1),=(-1,0,1),设平面AB1D1的法向量为n=(x,y,z),则,解得n=(2,-1,2),当A1E⊥平面AB1D1时A1E∥n,解得t=.
9.解析:(1)因为x轴垂直于平面ABB1A1,
所以n1=(1,0,0)是平面ABB1A1的一个法向量.
(2)因为正方体ABCD A1B1C1D1的棱长为3,CM=2MC1,
所以M,B,D1的坐标分别为(0,3,2),(3,3,0),(0,0,3),
因此=(3,0,-2),=(0,-3,1),
设n2=(x,y,z)是平面MBD1的法向量,
则n2⊥,n2⊥MD1,
所以,
取z=3,则x=2,y=1.于是n2=(2,1,3)是平面MBD1的一个法向量.
10.证明:(1)以B为坐标原点,BA、BC、BB1所在的直线分别为x轴、y轴、z轴建立空间直角坐标系,
如图所示,则B(0,0,0),D(0,2,2),B1(0,0,4),设BA=a,则A(a,0,0),
所以=(a,0,0),=(0,2,2),=(0,2,-2),=0,·=0+4-4=0,
即B1D⊥BA,B1D⊥BD.
又BA∩BD=B,因此B1D⊥平面ABD.
(2)由(1)知,E(0,0,3),G(,1,4),F(0,1,4),则=(,1,1),=(0,1,1),
·=0+2-2=0,·=0+2-2=0,即B1D⊥EG,B1D⊥EF.
又EG∩EF=E,EG,EF 平面EGF,因此B1D⊥平面EGF.
结合(1)可知平面EGF∥平面ABD.
核心素养升级练
1.答案:B
解析:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
A(2,0,0),E(1,2,0),F(0,2,1),A1(2,0,2),=(-1,2,0),=(-2,2,1),设平面AEF的法向量n=(x,y,z),则,取y=1,得n=(2,1,2),设P(a,2,c),0≤a≤2,0≤c≤2,则=(a-2,2,c-2),∵A1P平行于平面AEF,∴A1P·n=2(a-2)+2+2(c-2)=0,整理得a+c=3,∴线段A1P的长度||===,当且仅当a=c=时,线段A1P长度取最小值.故选B.
2.答案:3
解析:易得CD⊥DE,CD⊥DA,又平面ABCD⊥平面CDEF,平面ABCD∩平面CDEF=CD,又AD 平面ABCD,则AD⊥平面CDEF,
又DE 平面CDEF,则AD⊥DE,以D为原点建立如图所示空间直角坐标系,则D(0,0,0),B(1,1,0),A(1,0,0),E(0,0,1),C(0,2,0),
又=+=+=+(-)=+=(0,,),
同理可得=+=+=+=(,,),设平面DBN的法向量为n=(x,y,z),
则,令y=1,则n=(-1,1,-4),又=+=(-,,),
又AP∥平面DBN,则·n=+-=0,解得μ=3.
3.解析:(1)证明:因为AC=3,BC=4,AB=5,所以∠ACB=90°,
如图所示,在直三棱柱ABC A1B1C1中,以C为坐标原点,直线CA、CB、CC1分别为x轴、y轴、z轴,建立空间直角坐标系,
则C(0,0,0),A(3,0,0),C1(0,0,4),B(0,4,0),B1(0,4,4),
因为=(-3,0,0),=(0,-4,4),
所以·=0,⊥,即AC⊥BC1.
(2)若存在点D使AC1∥平面CDB1,
则=λ=(-3λ,4λ,0),0≤λ≤1,
D(3-3λ,4λ,0),=(3-3λ,4λ-4,-4),=(0,-4,-4),AC1=(-3,0,4),
因为AC1∥平面CDB1,所以存在实数m、n,使AC1=m+n成立,
则,解得λ=,
故在AB上存在点D使AC1∥平面CDB1,此时点D为AB的中点.
必备知识基础练 进阶训练第一层
1.已知平面α外的直线l的方向向量是a=(3,2,1),平面α的法向量是u=(-1,2,-1),则l与α的位置关系是( )
A.l⊥α B.l∥α
C.l与α相交但不垂直 D.l∥α或l α
2.已知直线l的方向向量为a=(1,1,2),平面α的法向量为n=(2,2,4),则( )
A.l∥α B.l⊥α
C.l α D.l与α相交
3.[2023·山西大同高二检测]已知平面α和平面β的法向量分别为m=(3,1,-5),n=(-6,-2,10),则( )
A.α⊥β
B.α∥β
C.α与β相交但不垂直
D.以上都不对
4.[2023·安徽宿州高二检测]若向量a=(1,1,-1)是直线l的一个方向向量,n=(-1,2,2)是平面α的一个法向量,则直线l与平面α的位置关系是( )
A.平行 B.垂直
C.直线l在平面α内 D.相交但不垂直
5.已知A(1,0,0),B(0,1,0),C(0,0,1),则下列向量是平面ABC法向量的是( )
A.(-1,1,1) B.(1,1,1)
C.(-,,-) D.(,,-)
6.(多选)若v为直线l的方向向量,m,n分别为平面α,β的法向量(α,β不重合),则下列说法正确的有( )
A.v∥m l∥α B.v⊥m l⊥α
C.m∥n α∥β D.m⊥n α⊥β
7.法向量分别是n=(1,-1,2),m=(-2,0,3)的两个平面的位置关系是________________.
8.[2023·北京北师大附中高二检测]已知A(1,0,0),B(0,2,0),C(0,0,3),则平面ABC的一个法向量的坐标为________.
关键能力综合练 进阶训练第二层
1.已知u是直线l的方向向量,n是平面α的法向量,则“l α”是“u⊥n”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
2.已知向量=(2,4,x),平面α的一个法向量n=(1,y,3),若AB∥α,则( )
A.x=6,y=2
B.x=2,y=6
C.3x+4y+2=0
D.4x+3y+2=0
3.已知平面α的法向量为(2,-4,-2),平面β的法向量为(-1,2,k),若α∥β,则k=( )
A.-2 B.-1
C.1 D.2
4.[2023·福建泉州高二检测]已知点A(2,-1,2)在平面α内,n=(3,1,2)是平面α的一个法向量,则下列各点在平面α内的是( )
A.(1,-1,1) B.(1,3,)
C.(1,-3,) D.(-1,3,-)
5.[2023·山东青岛高二检测]已知直线l和平面ABC,若直线l的方向向量为n=(1,-2,-5),向量=(1,0,-1),=(2,1,0),则下列结论一定正确的为( )
A.l⊥平面ABC
B.l与平面ABC相交,但不垂直
C.l∥直线BC
D.l∥平面ABC或l 平面ABC
6.[2023·福建厦门高二测试](多选)如图,直三棱柱ABC A1B1C1中,CA⊥CB,CA=CB=CC1,D,E,M分别为B1C1,CC1,AB1的中点,点N是棱AC上一动点,则( )
A.MN⊥BC1
B.存在点N,使MN⊥平面BC1N
C.MN∥平面A1DE
D.存在点N,使MN∥DE
7.已知向量a=(1-m,1,m)是直线l的一个方向向量,向量n=(-2,m,1)是平面α的一个法向量,若直线l⊥平面α,则实数m的值为________.
8.在长方体ABCD A1B1C1D1中,AB=2,BC=CC1=1,若在CD上存在点E,使得A1E⊥平面AB1D1,则DE=________.
9.[2023·广东江门高二测试]如图,在棱长为3的正方体ABCD A1B1C1D1中,点M在棱C1C上,且CM=2MC1.以D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系.
(1)求平面ABB1A1的一个法向量;
(2)求平面MD1B的一个法向量.
10.
在直三棱柱ABC A1B1C1中,∠ABC=90°,BC=2,CC1=4,点E在线段BB1上,且EB1=1,D,F,G分别为CC1,C1B1,C1A1的中点.
(1)证明:B1D⊥平面ABD;
(2)证明:平面EGF∥平面ABD.
核心素养升级练 进阶训练第三层
1.
如图,在棱长为2的正方体ABCD A1B1C1D1中,点E,F分别是棱BC,CC1的中点,P是侧面BCC1B1内一点,若A1P平行于平面AEF,则线段A1P长度的最小值为( )
A. B.
C. D.
2.已知梯形ABCD和矩形CDEF.在平面图形中,AB=AD=DE=CD=1,CD⊥AE.现将矩形CDEF沿CD进行如图所示的翻折,满足平面ABCD垂直于平面CDEF.设=2,=μ,若AP∥平面DBN,则实数μ的值为________.
3.如图所示,在直三棱柱ABC A1B1C1中,AC=3,BC=4,AB=5,AA1=4.
(1)求证:AC⊥BC1;
(2)在AB上是否存在点D,使得AC1∥平面CDB1,若存在,确定点D的位置并说明理由,若不存在,说明理由.
1.4.1 用空间向量研究直线、平面的位置关系
必备知识基础练
1.答案:B
解析:由于a·u=(3,2,1)·(-1,2,-1)=-3+4-1=0,即a⊥u,由于l α,所以l∥α.故选B.
2.答案:B
解析:因为n=(2,2,4),a=(1,1,2),故可得n=2a,即n∥a,则直线l⊥α.故选B.
3.答案:B
解析:∵m=(3,1,-5),n=(-6,-2,10),∴n=-2m,
∴m∥n,∴α∥β.故选B.
4.答案:D
解析:a=(1,1,-1),n=(-1,2,2),a·n=-1+2-2=-1≠0,故a与n不垂直,即直线l与平面α不平行;若n=λa,则(-1,2,2)=λ(1,1,-1),无解,故a与n不平行,即直线l与平面α不垂直.故选D.
5.答案:B
解析:由题意,得=(-1,1,0),=(-1,0,1),设n=(x,y,z)为平面ABC的法向量,则,化简得,∴x=y=z.令x=1,有n=(1,1,1).故选B.
6.答案:CD
解析:对于A,v∥m l⊥α,错误;对于B,v⊥m l∥α或l α,错误;对于C,α,β不重合,m∥n α∥β,正确;对于D,m⊥n α⊥β,正确.故选CD.
7.答案:相交且不垂直
解析:假设存在λ∈R,使得n=λm,则,显然方程组无解,所以n,m不平行,即两个平面不平行;因为n·m=-2+6=4≠0,所以n与m不垂直,所以两个平面的位置关系是相交且不垂直.
8.答案:(6,3,2)(答案不唯一)
解析:因为A(1,0,0),B(0,2,0),C(0,0,3),所以=(-1,2,0),=(-1,0,3),设平面ABC的法向量为n=(x,y,z),则,即,令x=6,则y=3,z=2,所以n=(6,3,2).
关键能力综合练
1.答案:A
解析:已知u是直线l的方向向量,n是平面α的法向量,则u⊥n等价于l∥α或l α,所以“l α”是“u⊥n”的充分不必要条件.故选A.
2.答案:C
解析:因为AB∥α,则⊥n,则·n=2+4y+3x=0,故选C.
3.答案:C
解析:设平面α,平面β的法向量分别用m,n表示,由题意得m=(2,-4,-2)与n=(-1,2,k)平行,故m=tn,即,解得.故选C.
4.答案:B
解析:设平面α内的一点为P(x,y,z)(不与点A重合),则=(x-2,y+1,z-2),因为n=(3,1,2)是平面α的一个法向量,所以⊥n,所以·n=3(x-2)+(y+1)+2(z-2)=0,即3x+y+2z=9,对于A:3×1+(-1)+2×1=4≠9,故选项A不正确;对于B:3×1+3+2×=9,故选项B正确;对于C:3×1+(-3)+2×=3≠9,故选项C不正确;对于D:3×(-1)+3+2×=-3≠9,故选项D不正确.故选B.
5.答案:D
解析:n·=1+0+5=6≠0,n与不垂直,也即l与AB不垂直,所以直线l与平面α不垂直,A错;=-=(1,1,1),因此不存在实数k,使得n=k,所以n与不平行,即直线l与直线BC不平行,C错;设m=(x,y,z)是平面ABC的一个法向量,则,取x=1,则m=(1,-2,1),m·n=1+4-5=0,所以m⊥n,所以直线l与平面ABC平行或在平面ABC内,B错,D正确.故选D.
6.答案:AD
解析:A选项:连接BC1,B1C,由题可知四边形BCC1B1是正方形,则BC1⊥B1C,由题知平面BCC1B1⊥平面ABC,平面BCC1B1∩平面ABC=BC,AC⊥BC,AC 平面ABC,∴AC⊥平面BCC1B1,又BC1 平面BCC1B1,∴AC⊥BC1,又B1C∩AC=C,B1C,AC 平面AB1C,∴BC1⊥平面AB1C,∵MN 平面AB1C,∴BC1⊥MN.故A正确;
B选项:如图建立空间直角坐标系,设AC=BC=CC1=2,则C(0,0,0),B(2,0,0),A(0,2,0),B1(2,0,2),M(1,1,1),设N(0,t,0),0
D选项:由C项可知,N为AC中点满足题意,故D正确.
故选AD.
7.答案:-1
解析:因为直线l⊥平面α,则a=(1-m,1,m)与n=(-2,m,1)平行,故a=λn,即,解得m=-1,故实数m的值为-1.
8.答案:
解析:因为ABCD A1B1C1D1,所以DA,DC,DD1两两垂直,建立如图所示坐标系:
设DE=t,所以A1(1,0,1),E(0,t,0),A(1,0,0),B1(1,2,1),D1(0,0,1),则=(-1,t,-1),=(0,2,1),=(-1,0,1),设平面AB1D1的法向量为n=(x,y,z),则,解得n=(2,-1,2),当A1E⊥平面AB1D1时A1E∥n,解得t=.
9.解析:(1)因为x轴垂直于平面ABB1A1,
所以n1=(1,0,0)是平面ABB1A1的一个法向量.
(2)因为正方体ABCD A1B1C1D1的棱长为3,CM=2MC1,
所以M,B,D1的坐标分别为(0,3,2),(3,3,0),(0,0,3),
因此=(3,0,-2),=(0,-3,1),
设n2=(x,y,z)是平面MBD1的法向量,
则n2⊥,n2⊥MD1,
所以,
取z=3,则x=2,y=1.于是n2=(2,1,3)是平面MBD1的一个法向量.
10.证明:(1)以B为坐标原点,BA、BC、BB1所在的直线分别为x轴、y轴、z轴建立空间直角坐标系,
如图所示,则B(0,0,0),D(0,2,2),B1(0,0,4),设BA=a,则A(a,0,0),
所以=(a,0,0),=(0,2,2),=(0,2,-2),=0,·=0+4-4=0,
即B1D⊥BA,B1D⊥BD.
又BA∩BD=B,因此B1D⊥平面ABD.
(2)由(1)知,E(0,0,3),G(,1,4),F(0,1,4),则=(,1,1),=(0,1,1),
·=0+2-2=0,·=0+2-2=0,即B1D⊥EG,B1D⊥EF.
又EG∩EF=E,EG,EF 平面EGF,因此B1D⊥平面EGF.
结合(1)可知平面EGF∥平面ABD.
核心素养升级练
1.答案:B
解析:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
A(2,0,0),E(1,2,0),F(0,2,1),A1(2,0,2),=(-1,2,0),=(-2,2,1),设平面AEF的法向量n=(x,y,z),则,取y=1,得n=(2,1,2),设P(a,2,c),0≤a≤2,0≤c≤2,则=(a-2,2,c-2),∵A1P平行于平面AEF,∴A1P·n=2(a-2)+2+2(c-2)=0,整理得a+c=3,∴线段A1P的长度||===,当且仅当a=c=时,线段A1P长度取最小值.故选B.
2.答案:3
解析:易得CD⊥DE,CD⊥DA,又平面ABCD⊥平面CDEF,平面ABCD∩平面CDEF=CD,又AD 平面ABCD,则AD⊥平面CDEF,
又DE 平面CDEF,则AD⊥DE,以D为原点建立如图所示空间直角坐标系,则D(0,0,0),B(1,1,0),A(1,0,0),E(0,0,1),C(0,2,0),
又=+=+=+(-)=+=(0,,),
同理可得=+=+=+=(,,),设平面DBN的法向量为n=(x,y,z),
则,令y=1,则n=(-1,1,-4),又=+=(-,,),
又AP∥平面DBN,则·n=+-=0,解得μ=3.
3.解析:(1)证明:因为AC=3,BC=4,AB=5,所以∠ACB=90°,
如图所示,在直三棱柱ABC A1B1C1中,以C为坐标原点,直线CA、CB、CC1分别为x轴、y轴、z轴,建立空间直角坐标系,
则C(0,0,0),A(3,0,0),C1(0,0,4),B(0,4,0),B1(0,4,4),
因为=(-3,0,0),=(0,-4,4),
所以·=0,⊥,即AC⊥BC1.
(2)若存在点D使AC1∥平面CDB1,
则=λ=(-3λ,4λ,0),0≤λ≤1,
D(3-3λ,4λ,0),=(3-3λ,4λ-4,-4),=(0,-4,-4),AC1=(-3,0,4),
因为AC1∥平面CDB1,所以存在实数m、n,使AC1=m+n成立,
则,解得λ=,
故在AB上存在点D使AC1∥平面CDB1,此时点D为AB的中点.
