4.3.2独立性检验 课时作业(含解析)
文档属性
| 名称 | 4.3.2独立性检验 课时作业(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 188.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-11 00:00:00 | ||
图片预览




文档简介
4.3.2 独立性检验
必备知识基础练 进阶训练第一层
1.假设有两个分类变量x与y的2×2列联表如下表:
y1 y2
x1 a b
x2 c d
对于以下数据,对同一样本能说明x与y有关系的可能性最大的一组为( )
A.a=5,b=4,c=3,d=2
B.a=5,b=3,c=4,d=2
C.a=2,b=3,c=4,d=5
D.a=2,b=3,c=5,d=4
2.(多选)为了增强学生的身体素质,某校将冬天长跑作为一项制度固定下来,每天大课间例行跑操.为了调查学生喜欢跑步是否与性别有关,研究人员随机调查了相同人数的男、女学生,发现男生中有80%喜欢跑步,女生中有40%不喜欢跑步,且有95%的把握判断喜欢跑步与性别有关,但没有99%的把握判断喜欢跑步与性别有关,则被调查的男、女学生的总人数可能为( )
A.120 B.130
C.240 D.250
3.(多选)疫苗是为预防、控制传染病的发生、流行,用于人体预防接种的预防性生物制品,其前期研发过程中,一般都会进行动物保护测试,为了考察某种疫苗预防效果,在进行动物试验时,得到如下统计数据:
未发病 发病 总计
未注射疫苗 30
注射疫苗 40
总计 70 30 100
附表及公式:
α=P(χ2≥k) 0.05 0.01 0.005 0.001
k 3.841 6.635 7.879 10.828
χ2=,n=a+b+c+d.
现从试验动物中任取一只,取得“注射疫苗”的概率为0.5,则下列判断正确的是( )
A.注射疫苗发病的动物数为10
B.某个发病的小动物为未注射疫苗动物的概率为
C.能在犯错概率不超过0.005的前提下,认为疫苗有效
D.该疫苗的有效率约为80%
4.为了判断某高中学生是否选修文科与性别的关系,现随机抽取50名学生,得到2×2列联表:
理科 文科
男 13 10
女 7 20
根据表中数据,得到χ2=≈4.844,则认为选修文科与性别有关系出错的概率约为________.(参考数据:P(χ2≥3.841)=0.05,P(χ2≥6.635)=0.01)
5.某单位主管对50名员工进行了工作量的调查,了解男、女职工对工作量大小的看法是否存在差异,得到的数据如下:
请判断认为工作量的大小与性别是否有关.
6.2021年9月,教育部印发《关于全面加强和改进新时代学校卫生与健康教育工作的意见》中指出:中小学生各项身体素质有所改善,大学生整体下降.某高校为提高学生身体素质,号召全校学生参加体育锻炼,结合“微信运动”APP每日统计运动情况,对每日平均运动10 000步或以上的学生授予“运动达人”称号,低于10 000步称为“参与者”,统计了200名学生在某月的运动数据,结果如下:
运动达人 参与者 合计
男生 70
女生 80
合计 80 200
(1)完善2×2列联表并说明:是否有99%的把握认为获得“运动达人”称号与性别有关?
(2)从全校运动“运动达人”中按性别分层抽取8人,再从8人中选取4人参加特训,将男生人数记为X,求X的分布列.
参考公式:χ2=,n=a+b+c+d.
α=P(χ2≥k) 0.10 0.05 0.010 0.005 0.001
k 2.706 3.841 6.635 7.879 10.828
关键能力综合练 进阶训练第二层
7.假设有两个分类变量X与Y,它们的可能取值分别为{x1,x2}和{y1,y2},其2×2列联表为
YX y1 y2 合计
x1 10 18 28
x2 m 26 m+26
总计 m+10 44 m+54
则当整数m取( )时,X与Y的关系最弱
A.8 B.9
C.14 D.19
8.(多选)千百年来,我国劳动人民在生产实践中根据云的形状,走向,速度,厚度,颜色等的变化,总结了丰富的“看云识天气”的经验,并将这些经验编成谚语,如“天上钩钩云,地上雨淋淋”“日落云里走,雨在半夜后”……小波同学为了验证“日落云里走,雨在半夜后”,随机观察了他所在地区的100天日落情况和后半夜天气,得到如下2×2列联表,
单位:天
并计算得到χ2≈19.05,下列小波对该地区天气的判断正确的是( )
A.后半夜下雨的概率约为
B.未出现“日落云里走”时,后半夜下雨的概率约为
C.根据α=0.001的独立性检验,可以推断“日落云里走”是否出现与“后半夜是否下雨”有关
D.根据α=0.001的独立性检验,若出现“日落云里走”,则后半夜有99.9%的可能会下雨
9.北京冬奥会的举办掀起了一阵冰雪运动的热潮.某高校在本校学生中对“喜欢滑冰是否与性别有关”做了一次调查,参与调查的学生中,男生人数是女生人数的3倍,有的男生喜欢滑冰,有的女生喜欢滑冰.若根据独立性检验的方法,有95%的把握认为是否喜欢滑冰和性别有关,则参与调查的男生人数可能为( )
参考公式:χ2=,其中n=a+b+c+d.
参考数据:
α=P(χ2≥k) 0.10 0.05 0.025 0.010
k 2.706 3.841 5.024 6.635
A.12 B.18
C.36 D.48
10.流感是流行性感冒的简称,是由流感病毒引起的一种呼吸道传染病.接种疫苗是预防流感的主要措施.某医疗研究所为了检验某流感疫苗预防感冒的作用,把500名使用疫苗的人与另外500名未使用疫苗的人一年中的感冒记录作比较,提出假设H0:“注射此种疫苗对预防流感无关”,利用2×2列联表计算得χ2≈6.789,经查临界值表知P(χ2≥6.635)=0.01.则下列结论正确的是( )
A.若某人未使用该疫苗,那么他在一年中有99%的可能性得感冒
B.在犯错误的概率不超过0.01的前提下认为“注射此种疫苗对预防流感有关”
C.这种疫苗预防感冒的有效率为99%
D.这种疫苗预防感冒的有效率为1%
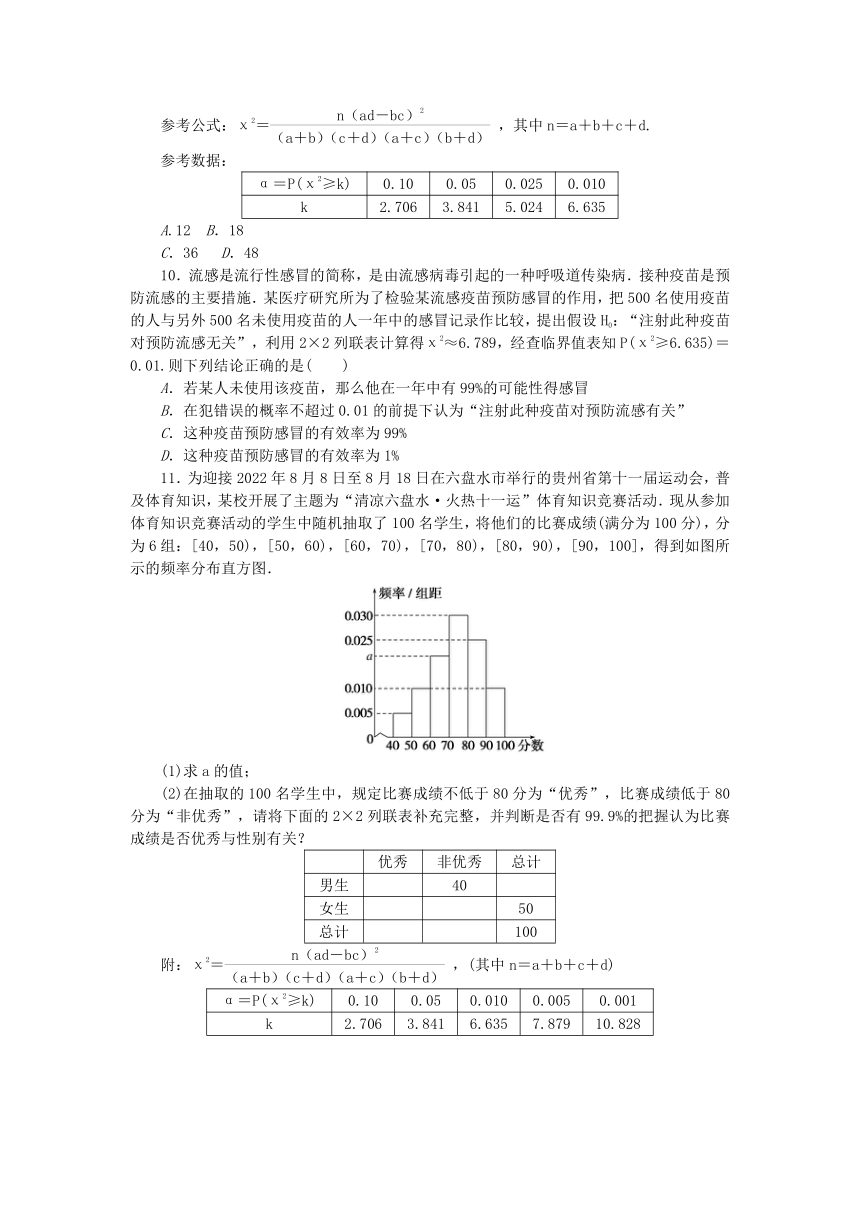
11.为迎接2022年8月8日至8月18日在六盘水市举行的贵州省第十一届运动会,普及体育知识,某校开展了主题为“清凉六盘水·火热十一运”体育知识竞赛活动.现从参加体育知识竞赛活动的学生中随机抽取了100名学生,将他们的比赛成绩(满分为100分),分为6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100],得到如图所示的频率分布直方图.
(1)求a的值;
(2)在抽取的100名学生中,规定比赛成绩不低于80分为“优秀”,比赛成绩低于80分为“非优秀”,请将下面的2×2列联表补充完整,并判断是否有99.9%的把握认为比赛成绩是否优秀与性别有关?
优秀 非优秀 总计
男生 40
女生 50
总计 100
附:χ2=,(其中n=a+b+c+d)
α=P(χ2≥k) 0.10 0.05 0.010 0.005 0.001
k 2.706 3.841 6.635 7.879 10.828
12.随着新冠疫情防控进入常态化,人们的生产生活逐步步入正轨.为拉动消费,某市政府分批发行2亿元政府消费券,为了解政府消费券使用人群的年龄结构情况,在发行完第一批政府消费券后,该市政府采用随机抽样的方法在全市市民中随机抽取了200人,对是否使用过政府消费券的情况进行调查,部分结果如下表所示,其中年龄在45岁及以下的人数占样本总数的,没使用过政府消费券的人数占样本总数的.
使用过政府消费券 没使用过政府消费券 总计
45岁及以下 80
45岁以上
总计 200
(1)请将题中表格补充完整,并判断是否有90%的把握认为该市市民是否使用政府消费券与年龄有关?
(2)现从45岁及以下的样本中按是否使用过政府消费券进行分层抽样,抽取6人做进一步访谈,然后再从这6人中随机抽取2人填写调查问卷,求这2人中至少有1人来自没使用过政府消费券的概率.
附:χ2=,其中n=a+b+c+d.
α=P(χ2≥k) 0.15 0.10 0.05 0.025
k 2.072 2.706 3.841 5.024
核心素养升级练 进阶训练第三层
13.PISA是经济合作与发展组织(OECD)于2000年发起的对基础教育进行跨国家(地区)、跨文化的评价项目,主要是对15岁在校生的科学、数学、阅读素养等核心素养进行测评,并对影响学生素养的关键因素进行问卷测查,以科学反映学生参与未来社会生活的能力,为教育教学改进提供有效证据.随着越来越多国家的加入,加之其科学、系统的整体设计,PISA已成为当前最具规模与影响力的国际性教育监测评估项目.
某校为了研究高一15岁学生的阅读素养情况是否与科学素养情况有关,随机抽取80名学生(15岁)进行阅读素养和科学素养测试,测试情况统计如下表:
科学素养“好” 科学素养“不好” 合计
阅读素养“好” 24 16 40
阅读素养“不好” 17 23 40
合计 41 39 80
(1)试求χ2的值,并判断是否有85%的把握认为阅读素养情况与科学素养情况有关;
(2)现从阅读素养“好”的40名学生中,用分层抽样的方法抽取10人组成一个互助小组.再从这10人中任意抽取3人负责沟通协调工作,设其中抽到科学素养“不好”的人数为X,求X的分布列和数学期望.
附表及公式:
α=P(χ2≥k) 0.50 0.40 0.25 0.15 0.10 0.05 0.025
k 0.455 0.708 1.323 2.072 2.706 3.841 5.024
χ2=,其中n=a+b+c+d.
14.某城市为了了解高中生的身高情况,从某次全市高中生体检中抽取了一所学校的n名学生的身高数据,整理分组成区间[140,150],(150,160],(160,170],(170,180],(180,190],单位:厘米,并画出了频率分布直方图如下,已知从左到右前三个小组频率之比为2∶3∶4,其中第二小组有15人.
(1)求样本频数n的值;
(2)以此校的样本数据来估计全市的总体数据,若从全市所有高中学生(人数很多)中任选三人,设X表示身高超过160厘米的学生人数,求X的分布列及期望;
(3)某班主任对全班50名学生进行了作业量多少的调查.数据如下表:
认为作业多 认为作业不多 合计
喜欢玩游戏 18 9 27
不喜欢玩游戏 8 15 23
合计 26 24 50
试通过计算说明在犯错误的概率不超过多少的前提下认为喜欢玩游戏与作业量的多少有关系.
附:
α=P(χ2≥k) 0.05 0.025 0.010 0.005 0.001
k 3.841 5.024 6.635 7.879 10.828
χ2=,n=a+b+c+d.
15.大型综艺节目《最强大脑》中,有一个游戏叫做盲拧魔方,就是玩家先观察魔方状态并进行记忆,记住后蒙住眼睛快速还原魔方,盲拧在外人看来很神奇,其实原理是十分简单的,要学会盲拧也是很容易的.根据调查显示,是否喜欢盲拧魔方与性别有关.为了验证这个结论,某兴趣小组随机抽取了50名魔方爱好者进行调查,得到的情况如下表所示:
喜欢盲拧 不喜欢盲拧 总计
男 22 30
女 12
总计 50
表1
并邀请这30名男生参加盲拧三阶魔方比赛,其完成情况如下表所示:
成功完成时间(分钟) [0,10) [10,20) [20,30) [30,40]
人数 10 10 5 5
表2
(1)将表1补充完整,并判断能否在犯错误的概率不超过0.025的前提下认为是否喜欢盲拧与性别有关?
(2)根据表2中的数据,求这30名男生成功完成盲拧的平均时间(同一组中的数据用该组区间的中点值代替);
(3)现从表2中成功完成时间在[0,10)内的10名男生中任意抽取3人对他们的盲拧情况进行视频记录,记成功完成时间在[0,10)内的甲、乙、丙3人中被抽到的人数为X,求X的分布列及数学期望E(X).
附参考公式及数据:
χ2=,其中n=a+b+c+d.
α=P(χ2≥k) 0.10 0.05 0.025 0.010 0.005 0.001
k 2.706 3.841 5.024 6.635 7.879 10.828
4.3.2 独立性检验
必备知识基础练
1.答案:D
解析:对于两个分类变量x与y而言,|ad-bc|的值越大,说明x与y有关系的可能性最大.
对于A选项,|ad-bc|=|5×2-4×3|=2,
对于B选项,|ad-bc|=|5×2-3×4|=2,
对于C选项,|ad-bc|=|2×5-3×4|=2,
对于D选项,|ad-bc|=|2×4-3×5|=7,
显然D中|ad-bc|最大.故选D.
2.答案:AB
解析:依题意,设男、女学生的人数均为5x(x∈N*),则被调查的男、女学生的总人数为10x.建立如下2×2列联表:
喜欢跑步 不喜欢跑步 总计
男 4x x 5x
女 3x 2x 5x
总计 7x 3x 10x
则χ2==,又3.841<≤6.635,所以80.661<10x≤139.335.故选AB.
3.答案:ABD
解析:完善列联表如下:
未发病 发病 总计
未注射疫苗 30 20 50
注射疫苗 40 10 50
总计 70 30 100
由列联表知,A正确;
=,B正确;
χ2=≈4.762∈(3.841,6.635),
不能在犯错概率不超过0.005的前提下,认为疫苗有效,C错误;
疫苗的有效率约为=80%,D正确.
故选ABD.
4.答案:0.05
解析:因为χ2≈4.844>3.841,P(χ2≥3.841)=0.05,所以认为选修文科与性别有关系出错的概率约为0.05.
5.解析:P(Y=1|X=1)===≈0.667.
P(Y=1|X=0)==≈0.348,
所以认为工作量的大小与性别有关系,男职工更加认为工作量大.
6.解析:(1)由题意完善2×2列联表如下:
运动达人 参与者 合计
男生 50 70 120
女生 30 50 80
合计 80 120 200
此时:χ2==≈0.35<6.635.
所以没有99%的把握认为获得“运动达人”称号与性别有关.
(2)由题意知:选取的8人运动参与者中男生5人,女生3人,X的所有可能情况为:1、2、3、4,
且P(X=1)==,P(X=2)==,
P(X=3)==,P(X=4)==.
X的分布列为:
X 1 2 3 4
P
关键能力综合练
7.答案:C
解析:在两个分类变量的列联表中,当|ad-bc|的值越小时,认为两个分类变量有关的可能性越小.
令|ad-bc|=0,得10×26=18m,解得m≈14.4,
又m为整数,所以当m=14时,X与Y的关系最弱.
故选C.
8.答案:AC
解析:由题意,把频率看作概率,可得后半夜下雨的概率约为=,故A判断正确;
未出现“日落云里走”时,后半夜下雨的概率约为=,故B判断错误;
由χ2≈19.05>10.828=x0.001,根据α=0.001的独立性检验,认为“‘日落云里走’是否出现”与“当晚后半夜是否下雨”有关,故C判断正确,D判断错误.
故选AC.
9.答案:C
解析:设男生人数为3x,则女生人数为x,且x∈N*,
可得列联表如下:
男生 女生 合计
喜欢滑冰 2x
不喜欢滑冰 x
合计 3x x 4x
所以χ2==,
因为有95%的把握认为是否喜欢滑冰和性别有关,
所以∈(3.841,5.024],解得11.20所以33.60<3x≤43.96,
结合选项只有36∈(33.60,43.96].
故选C.
10.答案:B
解析:根据独立性检验,可以得到B正确,其余的理解均不正确.故选B.
11.解析:(1)由频率分布直方图各小矩形面积之和为1可知:
10×(0.005+0.010+a+0.030+0.025+0.010)=1,解得a=0.020.
(2)由图可知:
低于80分的频率为:10×(0.005+0.010+0.020+0.030)=0.65,
所以非优秀的人数为:100×0.65=65人,据此可知2×2列联表如下:
优秀 非优秀 总计
男生 10 40 50
女生 25 25 50
总计 35 65 100
可知:χ2=≈9.890<10.828,
所以没有99.9%的把握认为比赛成绩是否优秀与性别有关.
12.解析:(1)由题意得,总人数为200人,年龄在45岁及以下的人数为200×=120人,
没使用过政府消费券的人数为200×=60人,
完成表格如下:
使用过政府消费券 没使用过政府消费券 总计
45岁及以下 80 40 120
45岁以上 60 20 80
总计 140 60 200
由列联表可知χ2==≈1.587<2.706,
所以没有90%的把握认为该市市民是否使用政府消费券与年龄有关.
(2)由题意可知,从45岁及以下的市民中采用分层抽样的方法可以抽取使用过政府消费券的市民4人,记为A,B,C,D,没使用过政府消费券的市民2人,记为a,b,
从这6人中随机抽取2人的方法有:
AB,AC,AD,Aa,Ab,BC,BD,Ba,Bb,CD,Ca,Cb,Da,ab,Db,共15种,
其中这2人中至少有1人来自没使用过政府消费券的方法有:
Aa,Ab,Ba,Bb,Ca,Cb,Da,Db,ab,共9种,
故所求的概率为P==.
核心素养升级练
13.解析:(1)χ2=≈2.452>2.072,
有85%的把握认为阅读素养情况与科学素养情况有关.
(2)由分层抽样知抽取的10人,科学素养“好”的有6人,科学素养“不好”的有4人,因此X的取值依次为0,1,2,3,
P(X=0)==,
P(X=1)==,
P(X=2)==,
P(X=3)==,
X的分布列为:
X 0 1 2 3
P
E(X)=0×+1×+2×+3×=.
14.解析:(1)设前三个小组的频率分别为p1,p2,p3,
由条件得,
解得p1=,p2=,p3=,
由p2== n=60.
(2)由(1)知一个高中生身高超过160厘米的概率为
p=p3+(0.005+0.020)×10=,
X可取0,1,2,3,
P(X=0)=C=,
P(X=1)=C·=,
P(X=2)=C·=,
P(X=3)=C=,
故分布列为:
X 0 1 2 3
P
E(X)=0×+1×+2×+3×=.
(3)χ2=≈5.059>5.024,
所以在犯错误的概率不超过0.025的前提下认为喜欢玩游戏与作业量的多少有关系.
15.解析:(1)依题意,补充完整的表1如下:
喜欢盲拧 不喜欢盲拧 总计
男 22 8 30
女 8 12 20
总计 30 20 50
所以χ2==≈5.556>5.024,
所以能在犯错误的概率不超过0.025的前提下认为是否喜欢盲拧与性别有关.
(2)依题意,所求平均时间为5×+15×+25×+35×=(分钟).
(3)依题意,X的可能取值为0,1,2,3,
故P(X=0)==,P(X=1)==,
P(X=2)==,P(X=3)==,
故X的分布列为
X 0 1 2 3
P
故E(X)=0×+1×+2×+3×=.
必备知识基础练 进阶训练第一层
1.假设有两个分类变量x与y的2×2列联表如下表:
y1 y2
x1 a b
x2 c d
对于以下数据,对同一样本能说明x与y有关系的可能性最大的一组为( )
A.a=5,b=4,c=3,d=2
B.a=5,b=3,c=4,d=2
C.a=2,b=3,c=4,d=5
D.a=2,b=3,c=5,d=4
2.(多选)为了增强学生的身体素质,某校将冬天长跑作为一项制度固定下来,每天大课间例行跑操.为了调查学生喜欢跑步是否与性别有关,研究人员随机调查了相同人数的男、女学生,发现男生中有80%喜欢跑步,女生中有40%不喜欢跑步,且有95%的把握判断喜欢跑步与性别有关,但没有99%的把握判断喜欢跑步与性别有关,则被调查的男、女学生的总人数可能为( )
A.120 B.130
C.240 D.250
3.(多选)疫苗是为预防、控制传染病的发生、流行,用于人体预防接种的预防性生物制品,其前期研发过程中,一般都会进行动物保护测试,为了考察某种疫苗预防效果,在进行动物试验时,得到如下统计数据:
未发病 发病 总计
未注射疫苗 30
注射疫苗 40
总计 70 30 100
附表及公式:
α=P(χ2≥k) 0.05 0.01 0.005 0.001
k 3.841 6.635 7.879 10.828
χ2=,n=a+b+c+d.
现从试验动物中任取一只,取得“注射疫苗”的概率为0.5,则下列判断正确的是( )
A.注射疫苗发病的动物数为10
B.某个发病的小动物为未注射疫苗动物的概率为
C.能在犯错概率不超过0.005的前提下,认为疫苗有效
D.该疫苗的有效率约为80%
4.为了判断某高中学生是否选修文科与性别的关系,现随机抽取50名学生,得到2×2列联表:
理科 文科
男 13 10
女 7 20
根据表中数据,得到χ2=≈4.844,则认为选修文科与性别有关系出错的概率约为________.(参考数据:P(χ2≥3.841)=0.05,P(χ2≥6.635)=0.01)
5.某单位主管对50名员工进行了工作量的调查,了解男、女职工对工作量大小的看法是否存在差异,得到的数据如下:
请判断认为工作量的大小与性别是否有关.
6.2021年9月,教育部印发《关于全面加强和改进新时代学校卫生与健康教育工作的意见》中指出:中小学生各项身体素质有所改善,大学生整体下降.某高校为提高学生身体素质,号召全校学生参加体育锻炼,结合“微信运动”APP每日统计运动情况,对每日平均运动10 000步或以上的学生授予“运动达人”称号,低于10 000步称为“参与者”,统计了200名学生在某月的运动数据,结果如下:
运动达人 参与者 合计
男生 70
女生 80
合计 80 200
(1)完善2×2列联表并说明:是否有99%的把握认为获得“运动达人”称号与性别有关?
(2)从全校运动“运动达人”中按性别分层抽取8人,再从8人中选取4人参加特训,将男生人数记为X,求X的分布列.
参考公式:χ2=,n=a+b+c+d.
α=P(χ2≥k) 0.10 0.05 0.010 0.005 0.001
k 2.706 3.841 6.635 7.879 10.828
关键能力综合练 进阶训练第二层
7.假设有两个分类变量X与Y,它们的可能取值分别为{x1,x2}和{y1,y2},其2×2列联表为
YX y1 y2 合计
x1 10 18 28
x2 m 26 m+26
总计 m+10 44 m+54
则当整数m取( )时,X与Y的关系最弱
A.8 B.9
C.14 D.19
8.(多选)千百年来,我国劳动人民在生产实践中根据云的形状,走向,速度,厚度,颜色等的变化,总结了丰富的“看云识天气”的经验,并将这些经验编成谚语,如“天上钩钩云,地上雨淋淋”“日落云里走,雨在半夜后”……小波同学为了验证“日落云里走,雨在半夜后”,随机观察了他所在地区的100天日落情况和后半夜天气,得到如下2×2列联表,
单位:天
并计算得到χ2≈19.05,下列小波对该地区天气的判断正确的是( )
A.后半夜下雨的概率约为
B.未出现“日落云里走”时,后半夜下雨的概率约为
C.根据α=0.001的独立性检验,可以推断“日落云里走”是否出现与“后半夜是否下雨”有关
D.根据α=0.001的独立性检验,若出现“日落云里走”,则后半夜有99.9%的可能会下雨
9.北京冬奥会的举办掀起了一阵冰雪运动的热潮.某高校在本校学生中对“喜欢滑冰是否与性别有关”做了一次调查,参与调查的学生中,男生人数是女生人数的3倍,有的男生喜欢滑冰,有的女生喜欢滑冰.若根据独立性检验的方法,有95%的把握认为是否喜欢滑冰和性别有关,则参与调查的男生人数可能为( )
参考公式:χ2=,其中n=a+b+c+d.
参考数据:
α=P(χ2≥k) 0.10 0.05 0.025 0.010
k 2.706 3.841 5.024 6.635
A.12 B.18
C.36 D.48
10.流感是流行性感冒的简称,是由流感病毒引起的一种呼吸道传染病.接种疫苗是预防流感的主要措施.某医疗研究所为了检验某流感疫苗预防感冒的作用,把500名使用疫苗的人与另外500名未使用疫苗的人一年中的感冒记录作比较,提出假设H0:“注射此种疫苗对预防流感无关”,利用2×2列联表计算得χ2≈6.789,经查临界值表知P(χ2≥6.635)=0.01.则下列结论正确的是( )
A.若某人未使用该疫苗,那么他在一年中有99%的可能性得感冒
B.在犯错误的概率不超过0.01的前提下认为“注射此种疫苗对预防流感有关”
C.这种疫苗预防感冒的有效率为99%
D.这种疫苗预防感冒的有效率为1%
11.为迎接2022年8月8日至8月18日在六盘水市举行的贵州省第十一届运动会,普及体育知识,某校开展了主题为“清凉六盘水·火热十一运”体育知识竞赛活动.现从参加体育知识竞赛活动的学生中随机抽取了100名学生,将他们的比赛成绩(满分为100分),分为6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100],得到如图所示的频率分布直方图.
(1)求a的值;
(2)在抽取的100名学生中,规定比赛成绩不低于80分为“优秀”,比赛成绩低于80分为“非优秀”,请将下面的2×2列联表补充完整,并判断是否有99.9%的把握认为比赛成绩是否优秀与性别有关?
优秀 非优秀 总计
男生 40
女生 50
总计 100
附:χ2=,(其中n=a+b+c+d)
α=P(χ2≥k) 0.10 0.05 0.010 0.005 0.001
k 2.706 3.841 6.635 7.879 10.828
12.随着新冠疫情防控进入常态化,人们的生产生活逐步步入正轨.为拉动消费,某市政府分批发行2亿元政府消费券,为了解政府消费券使用人群的年龄结构情况,在发行完第一批政府消费券后,该市政府采用随机抽样的方法在全市市民中随机抽取了200人,对是否使用过政府消费券的情况进行调查,部分结果如下表所示,其中年龄在45岁及以下的人数占样本总数的,没使用过政府消费券的人数占样本总数的.
使用过政府消费券 没使用过政府消费券 总计
45岁及以下 80
45岁以上
总计 200
(1)请将题中表格补充完整,并判断是否有90%的把握认为该市市民是否使用政府消费券与年龄有关?
(2)现从45岁及以下的样本中按是否使用过政府消费券进行分层抽样,抽取6人做进一步访谈,然后再从这6人中随机抽取2人填写调查问卷,求这2人中至少有1人来自没使用过政府消费券的概率.
附:χ2=,其中n=a+b+c+d.
α=P(χ2≥k) 0.15 0.10 0.05 0.025
k 2.072 2.706 3.841 5.024
核心素养升级练 进阶训练第三层
13.PISA是经济合作与发展组织(OECD)于2000年发起的对基础教育进行跨国家(地区)、跨文化的评价项目,主要是对15岁在校生的科学、数学、阅读素养等核心素养进行测评,并对影响学生素养的关键因素进行问卷测查,以科学反映学生参与未来社会生活的能力,为教育教学改进提供有效证据.随着越来越多国家的加入,加之其科学、系统的整体设计,PISA已成为当前最具规模与影响力的国际性教育监测评估项目.
某校为了研究高一15岁学生的阅读素养情况是否与科学素养情况有关,随机抽取80名学生(15岁)进行阅读素养和科学素养测试,测试情况统计如下表:
科学素养“好” 科学素养“不好” 合计
阅读素养“好” 24 16 40
阅读素养“不好” 17 23 40
合计 41 39 80
(1)试求χ2的值,并判断是否有85%的把握认为阅读素养情况与科学素养情况有关;
(2)现从阅读素养“好”的40名学生中,用分层抽样的方法抽取10人组成一个互助小组.再从这10人中任意抽取3人负责沟通协调工作,设其中抽到科学素养“不好”的人数为X,求X的分布列和数学期望.
附表及公式:
α=P(χ2≥k) 0.50 0.40 0.25 0.15 0.10 0.05 0.025
k 0.455 0.708 1.323 2.072 2.706 3.841 5.024
χ2=,其中n=a+b+c+d.
14.某城市为了了解高中生的身高情况,从某次全市高中生体检中抽取了一所学校的n名学生的身高数据,整理分组成区间[140,150],(150,160],(160,170],(170,180],(180,190],单位:厘米,并画出了频率分布直方图如下,已知从左到右前三个小组频率之比为2∶3∶4,其中第二小组有15人.
(1)求样本频数n的值;
(2)以此校的样本数据来估计全市的总体数据,若从全市所有高中学生(人数很多)中任选三人,设X表示身高超过160厘米的学生人数,求X的分布列及期望;
(3)某班主任对全班50名学生进行了作业量多少的调查.数据如下表:
认为作业多 认为作业不多 合计
喜欢玩游戏 18 9 27
不喜欢玩游戏 8 15 23
合计 26 24 50
试通过计算说明在犯错误的概率不超过多少的前提下认为喜欢玩游戏与作业量的多少有关系.
附:
α=P(χ2≥k) 0.05 0.025 0.010 0.005 0.001
k 3.841 5.024 6.635 7.879 10.828
χ2=,n=a+b+c+d.
15.大型综艺节目《最强大脑》中,有一个游戏叫做盲拧魔方,就是玩家先观察魔方状态并进行记忆,记住后蒙住眼睛快速还原魔方,盲拧在外人看来很神奇,其实原理是十分简单的,要学会盲拧也是很容易的.根据调查显示,是否喜欢盲拧魔方与性别有关.为了验证这个结论,某兴趣小组随机抽取了50名魔方爱好者进行调查,得到的情况如下表所示:
喜欢盲拧 不喜欢盲拧 总计
男 22 30
女 12
总计 50
表1
并邀请这30名男生参加盲拧三阶魔方比赛,其完成情况如下表所示:
成功完成时间(分钟) [0,10) [10,20) [20,30) [30,40]
人数 10 10 5 5
表2
(1)将表1补充完整,并判断能否在犯错误的概率不超过0.025的前提下认为是否喜欢盲拧与性别有关?
(2)根据表2中的数据,求这30名男生成功完成盲拧的平均时间(同一组中的数据用该组区间的中点值代替);
(3)现从表2中成功完成时间在[0,10)内的10名男生中任意抽取3人对他们的盲拧情况进行视频记录,记成功完成时间在[0,10)内的甲、乙、丙3人中被抽到的人数为X,求X的分布列及数学期望E(X).
附参考公式及数据:
χ2=,其中n=a+b+c+d.
α=P(χ2≥k) 0.10 0.05 0.025 0.010 0.005 0.001
k 2.706 3.841 5.024 6.635 7.879 10.828
4.3.2 独立性检验
必备知识基础练
1.答案:D
解析:对于两个分类变量x与y而言,|ad-bc|的值越大,说明x与y有关系的可能性最大.
对于A选项,|ad-bc|=|5×2-4×3|=2,
对于B选项,|ad-bc|=|5×2-3×4|=2,
对于C选项,|ad-bc|=|2×5-3×4|=2,
对于D选项,|ad-bc|=|2×4-3×5|=7,
显然D中|ad-bc|最大.故选D.
2.答案:AB
解析:依题意,设男、女学生的人数均为5x(x∈N*),则被调查的男、女学生的总人数为10x.建立如下2×2列联表:
喜欢跑步 不喜欢跑步 总计
男 4x x 5x
女 3x 2x 5x
总计 7x 3x 10x
则χ2==,又3.841<≤6.635,所以80.661<10x≤139.335.故选AB.
3.答案:ABD
解析:完善列联表如下:
未发病 发病 总计
未注射疫苗 30 20 50
注射疫苗 40 10 50
总计 70 30 100
由列联表知,A正确;
=,B正确;
χ2=≈4.762∈(3.841,6.635),
不能在犯错概率不超过0.005的前提下,认为疫苗有效,C错误;
疫苗的有效率约为=80%,D正确.
故选ABD.
4.答案:0.05
解析:因为χ2≈4.844>3.841,P(χ2≥3.841)=0.05,所以认为选修文科与性别有关系出错的概率约为0.05.
5.解析:P(Y=1|X=1)===≈0.667.
P(Y=1|X=0)==≈0.348,
所以认为工作量的大小与性别有关系,男职工更加认为工作量大.
6.解析:(1)由题意完善2×2列联表如下:
运动达人 参与者 合计
男生 50 70 120
女生 30 50 80
合计 80 120 200
此时:χ2==≈0.35<6.635.
所以没有99%的把握认为获得“运动达人”称号与性别有关.
(2)由题意知:选取的8人运动参与者中男生5人,女生3人,X的所有可能情况为:1、2、3、4,
且P(X=1)==,P(X=2)==,
P(X=3)==,P(X=4)==.
X的分布列为:
X 1 2 3 4
P
关键能力综合练
7.答案:C
解析:在两个分类变量的列联表中,当|ad-bc|的值越小时,认为两个分类变量有关的可能性越小.
令|ad-bc|=0,得10×26=18m,解得m≈14.4,
又m为整数,所以当m=14时,X与Y的关系最弱.
故选C.
8.答案:AC
解析:由题意,把频率看作概率,可得后半夜下雨的概率约为=,故A判断正确;
未出现“日落云里走”时,后半夜下雨的概率约为=,故B判断错误;
由χ2≈19.05>10.828=x0.001,根据α=0.001的独立性检验,认为“‘日落云里走’是否出现”与“当晚后半夜是否下雨”有关,故C判断正确,D判断错误.
故选AC.
9.答案:C
解析:设男生人数为3x,则女生人数为x,且x∈N*,
可得列联表如下:
男生 女生 合计
喜欢滑冰 2x
不喜欢滑冰 x
合计 3x x 4x
所以χ2==,
因为有95%的把握认为是否喜欢滑冰和性别有关,
所以∈(3.841,5.024],解得11.20
结合选项只有36∈(33.60,43.96].
故选C.
10.答案:B
解析:根据独立性检验,可以得到B正确,其余的理解均不正确.故选B.
11.解析:(1)由频率分布直方图各小矩形面积之和为1可知:
10×(0.005+0.010+a+0.030+0.025+0.010)=1,解得a=0.020.
(2)由图可知:
低于80分的频率为:10×(0.005+0.010+0.020+0.030)=0.65,
所以非优秀的人数为:100×0.65=65人,据此可知2×2列联表如下:
优秀 非优秀 总计
男生 10 40 50
女生 25 25 50
总计 35 65 100
可知:χ2=≈9.890<10.828,
所以没有99.9%的把握认为比赛成绩是否优秀与性别有关.
12.解析:(1)由题意得,总人数为200人,年龄在45岁及以下的人数为200×=120人,
没使用过政府消费券的人数为200×=60人,
完成表格如下:
使用过政府消费券 没使用过政府消费券 总计
45岁及以下 80 40 120
45岁以上 60 20 80
总计 140 60 200
由列联表可知χ2==≈1.587<2.706,
所以没有90%的把握认为该市市民是否使用政府消费券与年龄有关.
(2)由题意可知,从45岁及以下的市民中采用分层抽样的方法可以抽取使用过政府消费券的市民4人,记为A,B,C,D,没使用过政府消费券的市民2人,记为a,b,
从这6人中随机抽取2人的方法有:
AB,AC,AD,Aa,Ab,BC,BD,Ba,Bb,CD,Ca,Cb,Da,ab,Db,共15种,
其中这2人中至少有1人来自没使用过政府消费券的方法有:
Aa,Ab,Ba,Bb,Ca,Cb,Da,Db,ab,共9种,
故所求的概率为P==.
核心素养升级练
13.解析:(1)χ2=≈2.452>2.072,
有85%的把握认为阅读素养情况与科学素养情况有关.
(2)由分层抽样知抽取的10人,科学素养“好”的有6人,科学素养“不好”的有4人,因此X的取值依次为0,1,2,3,
P(X=0)==,
P(X=1)==,
P(X=2)==,
P(X=3)==,
X的分布列为:
X 0 1 2 3
P
E(X)=0×+1×+2×+3×=.
14.解析:(1)设前三个小组的频率分别为p1,p2,p3,
由条件得,
解得p1=,p2=,p3=,
由p2== n=60.
(2)由(1)知一个高中生身高超过160厘米的概率为
p=p3+(0.005+0.020)×10=,
X可取0,1,2,3,
P(X=0)=C=,
P(X=1)=C·=,
P(X=2)=C·=,
P(X=3)=C=,
故分布列为:
X 0 1 2 3
P
E(X)=0×+1×+2×+3×=.
(3)χ2=≈5.059>5.024,
所以在犯错误的概率不超过0.025的前提下认为喜欢玩游戏与作业量的多少有关系.
15.解析:(1)依题意,补充完整的表1如下:
喜欢盲拧 不喜欢盲拧 总计
男 22 8 30
女 8 12 20
总计 30 20 50
所以χ2==≈5.556>5.024,
所以能在犯错误的概率不超过0.025的前提下认为是否喜欢盲拧与性别有关.
(2)依题意,所求平均时间为5×+15×+25×+35×=(分钟).
(3)依题意,X的可能取值为0,1,2,3,
故P(X=0)==,P(X=1)==,
P(X=2)==,P(X=3)==,
故X的分布列为
X 0 1 2 3
P
故E(X)=0×+1×+2×+3×=.
