1.2空间向量基本定理 课时作业(含解析)
文档属性
| 名称 | 1.2空间向量基本定理 课时作业(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 316.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-11 09:50:13 | ||
图片预览




文档简介
1.2 空间向量基本定理
必备知识基础练 进阶训练第一层
1.已知点O,A,B,C为空间不共面的四点,且向量a=++,向量b=+-,则与a,b不能构成空间基底的向量是( )
A. B.
C. D.或
2.在空间四点O,A,B,C中,若{,,}是空间的一个基底,则下列命题不正确的是( )
A.O,A,B,C四点不共线
B.O,A,B,C四点共面,但不共线
C.O,A,B,C四点不共面
D.O,A,B,C四点中任意三点不共线
3.在三棱柱ABC DEF中,G为棱AD的中点,若=a,=b,=c,则=( )
A.-a+b-c
B.a-b+c
C.-a+b+c
D.-a+b+c
4.在平行六面体ABCD A1B1C1D1中,AC与BD的交点为M,设=a,=b,=c,则D1M=( )
A.-a+b+c B.a-b+c
C.a+b+c D.-a-b+c
5.[2023·江苏南通高二测试](多选)已知a,b,c是空间的三个单位向量,下列说法正确的是( )
A.若a∥b,b∥c,则a∥c
B.若a,b,c两两共面,则a,b,c共面
C.对于空间的任意一个向量p,总存在实数x,y,z,使得p=xa+yb+zc
D.若{a,b,c}是空间的一组基底,则{a+b,b+c,c+a}也是空间的一组基底
6.[2023·广东惠来一中高二检测](多选)若向量{a,b,c}构成空间的一个基底,则下列向量共面的是( )
A.a+b,a-b,a+2b B.a-b,a+c,b+c
C.a-b,c,a+b+c D.a-2b,b+c,a+c-b
7.已知四面体OABC,M,N分别是BC,OA的中点,且=a,=b,=c,则用a,b,c表示向量=________.
8.[2023·湖北武汉十七中高二检测]设{a,b,c}是空间的一个单位正交基底,且向量p=3a+b+c,若m=a+b,n=a-c,则用基底{m,n,c}表示向量p=____________.
关键能力综合练 进阶训练第二层
1.在正方体ABCD A1B1C1D1中,F,G分别为AB,CC1的中点,则( )
A.=++
B.=++
C.=++
D.=-+
2.[2023·山东潍坊高二检测]已知三棱柱ABC A1B1C1,点P为线段B1C1上一点,且B1P=,则=( )
A.++
B.++
C.+-
D.++
3.[2023·广东佛山高二测试]在四面体D ABC中,点G是△ABC的重心,设=a,=b,=c,则=( )
A.a+b+c B.a+b+c
C.a+b+c D.a+b+c
4.[2023·福建龙岩高二检测]在平行六面体ABCD A1B1C1D1中,点E是线段CD1的中点,=3,设=a,=b,AA1=c,则=( )
A.a+b-c B.-a-b-c
C.a+b+c D.-a-b+c
5.
如图,在平行六面体ABCD A1B1C1D1中,E,F分别在棱BB1和DD1上,且DF=DD1.记=x+y+zAA1,若x+y+z=,则=( )
A. B.
C. D.
6.[2023·辽宁丹东高二测试](多选)已知四棱柱ABCD A1B1C1D1的底面是平行四边形,且=a,=b,=c,则( )
A.a-b-c= B.a+b+c=
C.a+b-c=D.a-b+c=
7.已知在正方体ABCD A1B1C1D1中,若点F是侧面CD1的中心,且=+m-nAA1,则m=________.
8.
如图,在空间四边形ABCD中,∠ABD=∠CBD=,∠ABC=,BC=BD=1,AB=,则异面直线AB与CD所成角的大小是________.
9.[2023·浙江杭州高二检测]如图三棱柱ABC A1B1C1的所有棱长都相等,∠A1AB=∠A1AC=60°,点M为△ABC的重心,AM的延长线交BC于点N,连接A1M,设=a,=b,AA1=c.
(1)用a,b,c表示A1M;
(2)证明:A1M⊥AB.
10.
如图,正四面体ABCD(所有棱长均相等)的棱长为1,E,F,G,H分别是正四面体ABCD中各棱的中点,设=a,=b,=c.
(1)用a,b,c表示,并求的长;
(2)求与的夹角.
核心素养升级练 进阶训练第三层
1.
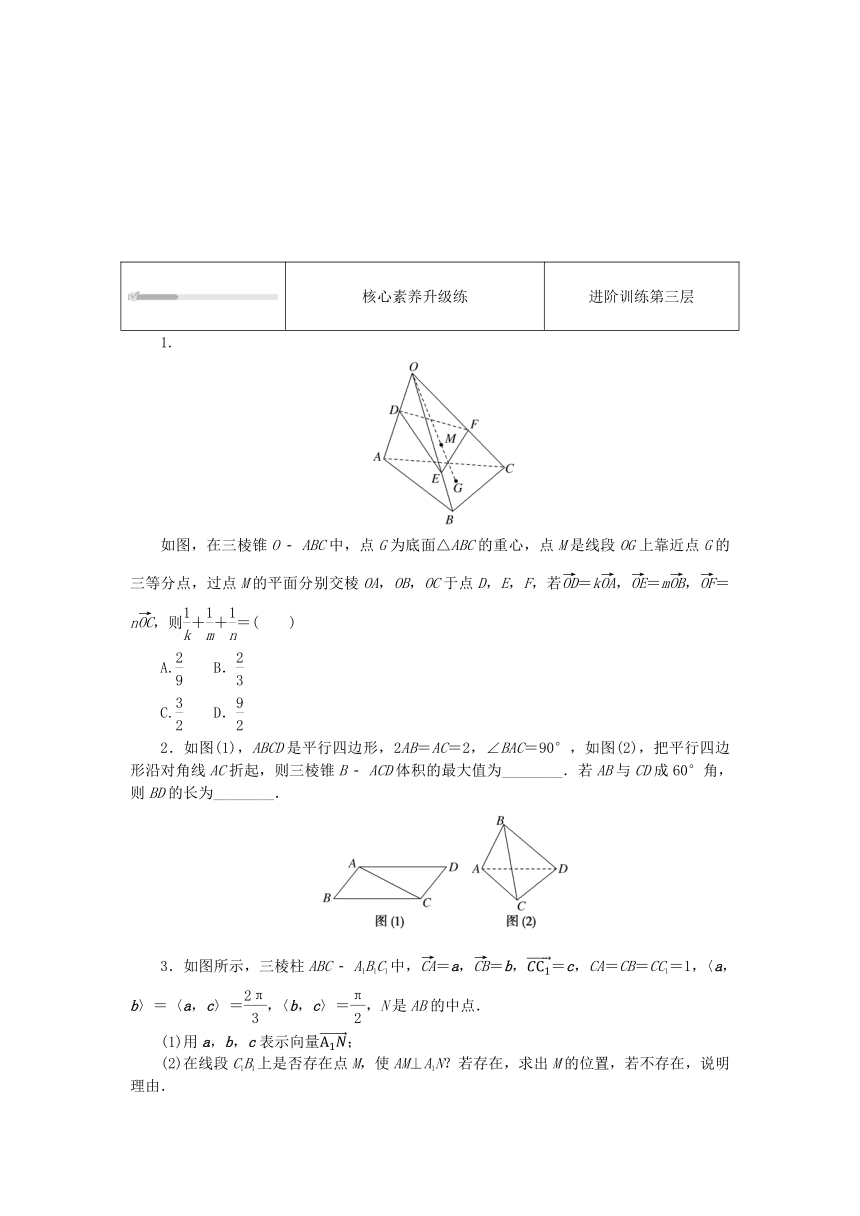
如图,在三棱锥O ABC中,点G为底面△ABC的重心,点M是线段OG上靠近点G的三等分点,过点M的平面分别交棱OA,OB,OC于点D,E,F,若=k,=m,=n,则++=( )
A. B.
C. D.
2.如图(1),ABCD是平行四边形,2AB=AC=2,∠BAC=90°,如图(2),把平行四边形沿对角线AC折起,则三棱锥B ACD体积的最大值为________.若AB与CD成60°角,则BD的长为________.
3.如图所示,三棱柱ABC A1B1C1中,=a,=b,=c,CA=CB=CC1=1,〈a,b〉=〈a,c〉=,〈b,c〉=,N是AB的中点.
(1)用a,b,c表示向量;
(2)在线段C1B1上是否存在点M,使AM⊥A1N?若存在,求出M的位置,若不存在,说明理由.
1.2 空间向量基本定理
必备知识基础练
1.答案:C
解析:∵=(a-b)=(++)-(+-),即a,b,共面,∴与a、b不能构成空间基底.故选C.
2.答案:B
解析:因为{,,}为基底,所以非零向量,,不在同一平面内,即O,A,B,C四点不共面,所以A、C、D选项说法正确,B错误.故选B.
3.答案:B
解析:=+=+=(-)+(-)=(a-b)+(c-a)=a-b+c.故选B.
4.答案:B
解析:
如图所示,∵=+=+=+(+),又=c,=-b,=a,∴=a-b+c.故选B.
5.答案:AD
解析:a,b,c是空间的三个单位向量,由a∥b,b∥c,则a∥c,故A正确;a,b,c两两共面,但是a,b,c不一定共面,a,b,c可能两两垂直,故B错误;由空间向量基本定理,可知只有当a,b,c不共面,才能作为基底,才能得到p=xa+yb+zc,故C错误;若{a,b,c}是空间的一组基底,则a,b,c不共面,可知{a+b,b+c,c+a}也不共面,所以{a+b,b+c,c+a}也是空间的一组基底,故D正确.故选AD.
6.答案:ABD
解析:对于A:由于向量{a,b,c}构成空间的一个基底,且满足a+2b=(a+b)-(a-b),故A正确;对于B:由于a-b=(a+c)-(b+c),故B正确;对于C:由于a+b+c≠m(a-b)+nc,故C错误;对于D:由于a-2b=(a+c-b)-(b+c),故D正确.故选ABD.
7.答案:a-b-c
解析:
如图,=+=-·(+)+=a-b-c.
8.答案:m+2n+3c
解析:设p=xm+yn+zc,
则x(a+b)+y(a-c)+zc=(x+y)a+xb+(z-y)c=3a+b+c,
故,解得,故p=m+2n+3c.
关键能力综合练
1.答案:C
解析:=+=++=++.故选C.
2.答案:D
解析:
由题意得=+=++,因为=,=,所以=++=++=++(-)=++.故选D.
3.答案:B
解析:
设E是BC中点,=+=+=+××(+)=+(+)=+(-+-)=+(+-2)=++=a+b+c.故选B.
4.答案:B
解析:因为E为CD1中点,所以=(+)=(+++)=++,=3 ==(+),所以=-=+---=---,即=-a-b-c.故选B.
5.答案:B
解析:设=λ,因为=+++=-λ-++=-λ-++AA1=-++(-λ)AA1,所以x=-1,y=1,z=-λ.因为x+y+z=-λ=,所以λ=.故选B.
6.答案:BC
解析:=-=+-=b+c-a,A选项错误;=++=a+b+c,B选项正确;=-=+-=a+b-c,C选项正确;=-=-(+)=b-a-c,D选项错误.故选BC.
7.答案:
解析:如图所示,可得=+=+(+)=++,又因为=+m-nAA1,所以m=,n=-.
8.答案:
解析:依题意可知CD==,·=·(-)=·-·=0+·=||||cos 45°=1.设直线AB与CD所成角为α,则cos α===,因为α∈,故α=.
9.解析:(1)因为△ABC为正三角形,点M为△ABC的重心,
所以N为BC的中点,
所以=+,=,
所以A1M=A1A+=-AA1+=-1++=a+b-c.
(2)证明:设三棱柱的棱长为m,
则A1M·=(a+b-c)·a
=a2+a·b-c·a
=|a|2+|a|·|b|cos -|c|·|a|cos
=m2+m2×-m2×=0.
所以A1M⊥AB.
10.解析:(1)因E,F分别为棱BC,AD的中点,而=a,=b,=c,
所以=++=-+=(-)-+=-a-b+c,
因正四面体ABCD的棱长为1,则a·b=b·c=c·a=|c||a|cos 60°=,
所以||=
==.
(2)依题意,=++=-a+c+(b-c)=-a+b+c,
因正四面体ABCD的棱长为1,有c·a=|c||a|cos 60°=,
因此·=-(a+b-c)·(a-b-c)=[(a-c)2-b2]=(a2+c2-2a·c-b2)=0,
所以⊥,即与的夹角为90°.
核心素养升级练
1.答案:D
解析:由题意可知,==(+)=[+×(+)]=[+(-)+(-)]=++.因为D,E,F,M四点共面,所以存在实数λ,μ,使=λ+μ,所以-=λ(-)+μ(-),所以=(1-λ-μ)+λ+μ=(1-λ-μ)k+λm+μn,所以,所以++=(1-λ-μ)+λ+μ=.故选D.
2.答案: 或
解析:由已知得,对于三棱锥B ACD,当AB⊥平面ACD时,三棱锥B ACD的体积最大,由2AB=AC=2,∠BAC=90°,ABCD是平行四边形,可得,S△ACD=S△ABC=×AB×AC=1,故VB ACD=×S△ACD×AB=×1×1=;=++,又因为AB与CD成60°角,故〈,〉=60°或〈,〉=120°,且〈,〉=90°,〈,〉=90°,||2=2+2+2+2·+2·+2·,故||2=1+4+1+2cos 60°或||2=1+4+1+2cos 120°,则||=或||=.
3.解析:(1)因为N是AB中点,所以=,
所以=+=+
=-+(-)=-a+b-c.
(2)假设存在点M,使AM⊥A1N,设=λ,(λ∈[0,1]),
显然λC1B1=λb,=++=c-a+λb,
因为AM⊥A1N,所以·=0,
即(c-a+λb)·(-a+b-c)=0,
∴-c·a+c·b-c2+a2-a·b+c·a-λa·b+λb2-λb·c=0.
∵CA=CB=CC1=1,〈a,b〉=〈a,c〉=,〈b,c〉=,
∴c·a-c2+a2-(+λ)a·b+λb2=0,
即×1×1×(-)-12+×12-(+λ)×1×1×(-)+λ·12=0,解得λ=,
所以当C1M=C1B1时,AM⊥A1N.
必备知识基础练 进阶训练第一层
1.已知点O,A,B,C为空间不共面的四点,且向量a=++,向量b=+-,则与a,b不能构成空间基底的向量是( )
A. B.
C. D.或
2.在空间四点O,A,B,C中,若{,,}是空间的一个基底,则下列命题不正确的是( )
A.O,A,B,C四点不共线
B.O,A,B,C四点共面,但不共线
C.O,A,B,C四点不共面
D.O,A,B,C四点中任意三点不共线
3.在三棱柱ABC DEF中,G为棱AD的中点,若=a,=b,=c,则=( )
A.-a+b-c
B.a-b+c
C.-a+b+c
D.-a+b+c
4.在平行六面体ABCD A1B1C1D1中,AC与BD的交点为M,设=a,=b,=c,则D1M=( )
A.-a+b+c B.a-b+c
C.a+b+c D.-a-b+c
5.[2023·江苏南通高二测试](多选)已知a,b,c是空间的三个单位向量,下列说法正确的是( )
A.若a∥b,b∥c,则a∥c
B.若a,b,c两两共面,则a,b,c共面
C.对于空间的任意一个向量p,总存在实数x,y,z,使得p=xa+yb+zc
D.若{a,b,c}是空间的一组基底,则{a+b,b+c,c+a}也是空间的一组基底
6.[2023·广东惠来一中高二检测](多选)若向量{a,b,c}构成空间的一个基底,则下列向量共面的是( )
A.a+b,a-b,a+2b B.a-b,a+c,b+c
C.a-b,c,a+b+c D.a-2b,b+c,a+c-b
7.已知四面体OABC,M,N分别是BC,OA的中点,且=a,=b,=c,则用a,b,c表示向量=________.
8.[2023·湖北武汉十七中高二检测]设{a,b,c}是空间的一个单位正交基底,且向量p=3a+b+c,若m=a+b,n=a-c,则用基底{m,n,c}表示向量p=____________.
关键能力综合练 进阶训练第二层
1.在正方体ABCD A1B1C1D1中,F,G分别为AB,CC1的中点,则( )
A.=++
B.=++
C.=++
D.=-+
2.[2023·山东潍坊高二检测]已知三棱柱ABC A1B1C1,点P为线段B1C1上一点,且B1P=,则=( )
A.++
B.++
C.+-
D.++
3.[2023·广东佛山高二测试]在四面体D ABC中,点G是△ABC的重心,设=a,=b,=c,则=( )
A.a+b+c B.a+b+c
C.a+b+c D.a+b+c
4.[2023·福建龙岩高二检测]在平行六面体ABCD A1B1C1D1中,点E是线段CD1的中点,=3,设=a,=b,AA1=c,则=( )
A.a+b-c B.-a-b-c
C.a+b+c D.-a-b+c
5.
如图,在平行六面体ABCD A1B1C1D1中,E,F分别在棱BB1和DD1上,且DF=DD1.记=x+y+zAA1,若x+y+z=,则=( )
A. B.
C. D.
6.[2023·辽宁丹东高二测试](多选)已知四棱柱ABCD A1B1C1D1的底面是平行四边形,且=a,=b,=c,则( )
A.a-b-c= B.a+b+c=
C.a+b-c=D.a-b+c=
7.已知在正方体ABCD A1B1C1D1中,若点F是侧面CD1的中心,且=+m-nAA1,则m=________.
8.
如图,在空间四边形ABCD中,∠ABD=∠CBD=,∠ABC=,BC=BD=1,AB=,则异面直线AB与CD所成角的大小是________.
9.[2023·浙江杭州高二检测]如图三棱柱ABC A1B1C1的所有棱长都相等,∠A1AB=∠A1AC=60°,点M为△ABC的重心,AM的延长线交BC于点N,连接A1M,设=a,=b,AA1=c.
(1)用a,b,c表示A1M;
(2)证明:A1M⊥AB.
10.
如图,正四面体ABCD(所有棱长均相等)的棱长为1,E,F,G,H分别是正四面体ABCD中各棱的中点,设=a,=b,=c.
(1)用a,b,c表示,并求的长;
(2)求与的夹角.
核心素养升级练 进阶训练第三层
1.
如图,在三棱锥O ABC中,点G为底面△ABC的重心,点M是线段OG上靠近点G的三等分点,过点M的平面分别交棱OA,OB,OC于点D,E,F,若=k,=m,=n,则++=( )
A. B.
C. D.
2.如图(1),ABCD是平行四边形,2AB=AC=2,∠BAC=90°,如图(2),把平行四边形沿对角线AC折起,则三棱锥B ACD体积的最大值为________.若AB与CD成60°角,则BD的长为________.
3.如图所示,三棱柱ABC A1B1C1中,=a,=b,=c,CA=CB=CC1=1,〈a,b〉=〈a,c〉=,〈b,c〉=,N是AB的中点.
(1)用a,b,c表示向量;
(2)在线段C1B1上是否存在点M,使AM⊥A1N?若存在,求出M的位置,若不存在,说明理由.
1.2 空间向量基本定理
必备知识基础练
1.答案:C
解析:∵=(a-b)=(++)-(+-),即a,b,共面,∴与a、b不能构成空间基底.故选C.
2.答案:B
解析:因为{,,}为基底,所以非零向量,,不在同一平面内,即O,A,B,C四点不共面,所以A、C、D选项说法正确,B错误.故选B.
3.答案:B
解析:=+=+=(-)+(-)=(a-b)+(c-a)=a-b+c.故选B.
4.答案:B
解析:
如图所示,∵=+=+=+(+),又=c,=-b,=a,∴=a-b+c.故选B.
5.答案:AD
解析:a,b,c是空间的三个单位向量,由a∥b,b∥c,则a∥c,故A正确;a,b,c两两共面,但是a,b,c不一定共面,a,b,c可能两两垂直,故B错误;由空间向量基本定理,可知只有当a,b,c不共面,才能作为基底,才能得到p=xa+yb+zc,故C错误;若{a,b,c}是空间的一组基底,则a,b,c不共面,可知{a+b,b+c,c+a}也不共面,所以{a+b,b+c,c+a}也是空间的一组基底,故D正确.故选AD.
6.答案:ABD
解析:对于A:由于向量{a,b,c}构成空间的一个基底,且满足a+2b=(a+b)-(a-b),故A正确;对于B:由于a-b=(a+c)-(b+c),故B正确;对于C:由于a+b+c≠m(a-b)+nc,故C错误;对于D:由于a-2b=(a+c-b)-(b+c),故D正确.故选ABD.
7.答案:a-b-c
解析:
如图,=+=-·(+)+=a-b-c.
8.答案:m+2n+3c
解析:设p=xm+yn+zc,
则x(a+b)+y(a-c)+zc=(x+y)a+xb+(z-y)c=3a+b+c,
故,解得,故p=m+2n+3c.
关键能力综合练
1.答案:C
解析:=+=++=++.故选C.
2.答案:D
解析:
由题意得=+=++,因为=,=,所以=++=++=++(-)=++.故选D.
3.答案:B
解析:
设E是BC中点,=+=+=+××(+)=+(+)=+(-+-)=+(+-2)=++=a+b+c.故选B.
4.答案:B
解析:因为E为CD1中点,所以=(+)=(+++)=++,=3 ==(+),所以=-=+---=---,即=-a-b-c.故选B.
5.答案:B
解析:设=λ,因为=+++=-λ-++=-λ-++AA1=-++(-λ)AA1,所以x=-1,y=1,z=-λ.因为x+y+z=-λ=,所以λ=.故选B.
6.答案:BC
解析:=-=+-=b+c-a,A选项错误;=++=a+b+c,B选项正确;=-=+-=a+b-c,C选项正确;=-=-(+)=b-a-c,D选项错误.故选BC.
7.答案:
解析:如图所示,可得=+=+(+)=++,又因为=+m-nAA1,所以m=,n=-.
8.答案:
解析:依题意可知CD==,·=·(-)=·-·=0+·=||||cos 45°=1.设直线AB与CD所成角为α,则cos α===,因为α∈,故α=.
9.解析:(1)因为△ABC为正三角形,点M为△ABC的重心,
所以N为BC的中点,
所以=+,=,
所以A1M=A1A+=-AA1+=-1++=a+b-c.
(2)证明:设三棱柱的棱长为m,
则A1M·=(a+b-c)·a
=a2+a·b-c·a
=|a|2+|a|·|b|cos -|c|·|a|cos
=m2+m2×-m2×=0.
所以A1M⊥AB.
10.解析:(1)因E,F分别为棱BC,AD的中点,而=a,=b,=c,
所以=++=-+=(-)-+=-a-b+c,
因正四面体ABCD的棱长为1,则a·b=b·c=c·a=|c||a|cos 60°=,
所以||=
==.
(2)依题意,=++=-a+c+(b-c)=-a+b+c,
因正四面体ABCD的棱长为1,有c·a=|c||a|cos 60°=,
因此·=-(a+b-c)·(a-b-c)=[(a-c)2-b2]=(a2+c2-2a·c-b2)=0,
所以⊥,即与的夹角为90°.
核心素养升级练
1.答案:D
解析:由题意可知,==(+)=[+×(+)]=[+(-)+(-)]=++.因为D,E,F,M四点共面,所以存在实数λ,μ,使=λ+μ,所以-=λ(-)+μ(-),所以=(1-λ-μ)+λ+μ=(1-λ-μ)k+λm+μn,所以,所以++=(1-λ-μ)+λ+μ=.故选D.
2.答案: 或
解析:由已知得,对于三棱锥B ACD,当AB⊥平面ACD时,三棱锥B ACD的体积最大,由2AB=AC=2,∠BAC=90°,ABCD是平行四边形,可得,S△ACD=S△ABC=×AB×AC=1,故VB ACD=×S△ACD×AB=×1×1=;=++,又因为AB与CD成60°角,故〈,〉=60°或〈,〉=120°,且〈,〉=90°,〈,〉=90°,||2=2+2+2+2·+2·+2·,故||2=1+4+1+2cos 60°或||2=1+4+1+2cos 120°,则||=或||=.
3.解析:(1)因为N是AB中点,所以=,
所以=+=+
=-+(-)=-a+b-c.
(2)假设存在点M,使AM⊥A1N,设=λ,(λ∈[0,1]),
显然λC1B1=λb,=++=c-a+λb,
因为AM⊥A1N,所以·=0,
即(c-a+λb)·(-a+b-c)=0,
∴-c·a+c·b-c2+a2-a·b+c·a-λa·b+λb2-λb·c=0.
∵CA=CB=CC1=1,〈a,b〉=〈a,c〉=,〈b,c〉=,
∴c·a-c2+a2-(+λ)a·b+λb2=0,
即×1×1×(-)-12+×12-(+λ)×1×1×(-)+λ·12=0,解得λ=,
所以当C1M=C1B1时,AM⊥A1N.
