1.1.3空间向量及其运算的坐标表示 课时作业(含解析)
文档属性
| 名称 | 1.1.3空间向量及其运算的坐标表示 课时作业(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 212.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-11 09:50:39 | ||
图片预览



文档简介
1.3 空间向量及其运算的坐标表示
必备知识基础练 进阶训练第一层
1.点A(2,0,22)关于y轴的对称点的坐标为( )
A.(-2,0,22) B.(2,0,-22)
C.(-2,0,-22) D.(2,0,22)
2.已知空间向量a=(1,2,-3),则向量a在坐标平面Oyz上的投影向量是( )
A.(0,2,3) B.(0,2,-3)
C.(1,2,0) D.(1,2,-3)
3.[2023·山东潍坊高二检测]已知向量a=(x,-2,6)与b=(1,y,-3)平行,则x+y=( )
A.1 B.-1
C.3 D.-3
4.在长方体ABCD A1B1C1D1中,已知AB=1,AD=2,AA1=3,M为B1C1的中点,则AM的长等于( )
A. B.
C.3 D.
5.(多选)已知向量a=(1,-2,-2),b=(6,-3,2),则下列结论正确的是( )
A.a+b=(7,-5,0) B.a-b=(5,-1,4)
C.a·b=8 D.|a|=
6.[2023·山东济南历城二中高二检测](多选)已知空间中三点A(0,1,0),B(1,-2,-1),C(-1,3,1),O是坐标原点,下列说法正确的是( )
A.点C关于平面Oxy对称的点为(1,-3,1)
B.||=
C.∥
D.⊥
7.[2023·山东德州高二检测]在空间直角坐标系中,已知=(3,2,1),=(1,0,5),=(-1,2,-1),点M为线段AB的中点,则||=________.
8.正方体ABCD A1B1C1D1中,M,N分别为棱BB1和B1C1的中点,则直线AM和CN所成角的余弦值为________.
关键能力综合练 进阶训练第二层
1.[2023·福建三明高二检测]向量a=(x,1,1),b=(1,y,1),c=(2,-4,2),且b⊥c,b⊥a,则a,c的夹角大小为( )
A. B.
C. D.
2.已知a=(1,2,-y),b=(x,1,2),且2b∥(a-b),则( )
A.x=,y=1 B.x=,y=-4
C.x=2,y= D.x=1,y=-1
3.已知正方体ABCD A′B′C′D′的棱长为a,对角线AC′与BD′相交于点O,则有( )
A.·=a2 B.·=a2
C.·=a D.·=a2
4.[2023·安徽泗县一中高二检测](多选)已知空间向量a=(-2,-1,1),b=(3,4,5),则下列结论正确的是( )
A.(2a+b)∥a
B.5|a|=|b|
C.a⊥(5a+4b)
D.a在b上的投影数量为-
5.[2023·山东青岛二中高二检测](多选)已知空间中三点A(2,1,-1),B(1,0,2),C(0,3,-1),则( )
A.||= B.AB⊥AC
C.cos ∠ABC= D.A,B,C三点共线
6.设x,y∈R,向量a=(3,2,1),b=(1,x,1),c=(y,4,2),且a⊥b,a∥c,则|c-2b|=________.
7.已知向量a=(2,-1,1),b=(1,3,1),则以a,b为邻边的平行四边形的面积为________.
8.已知向量a=(1,1,0),b=(m,0,2),cos 〈a,b〉=-,若向量a+kb与2a+b所成角为钝角,则实数k的范围是________.
9.[2023·山东潍坊高二检测]已知向量a=(1,1,0),b=(-1,0,c),且|a+b|=.
(1)求c的值;
(2)若ka+b与2a-b互相垂直,求实数k的值.
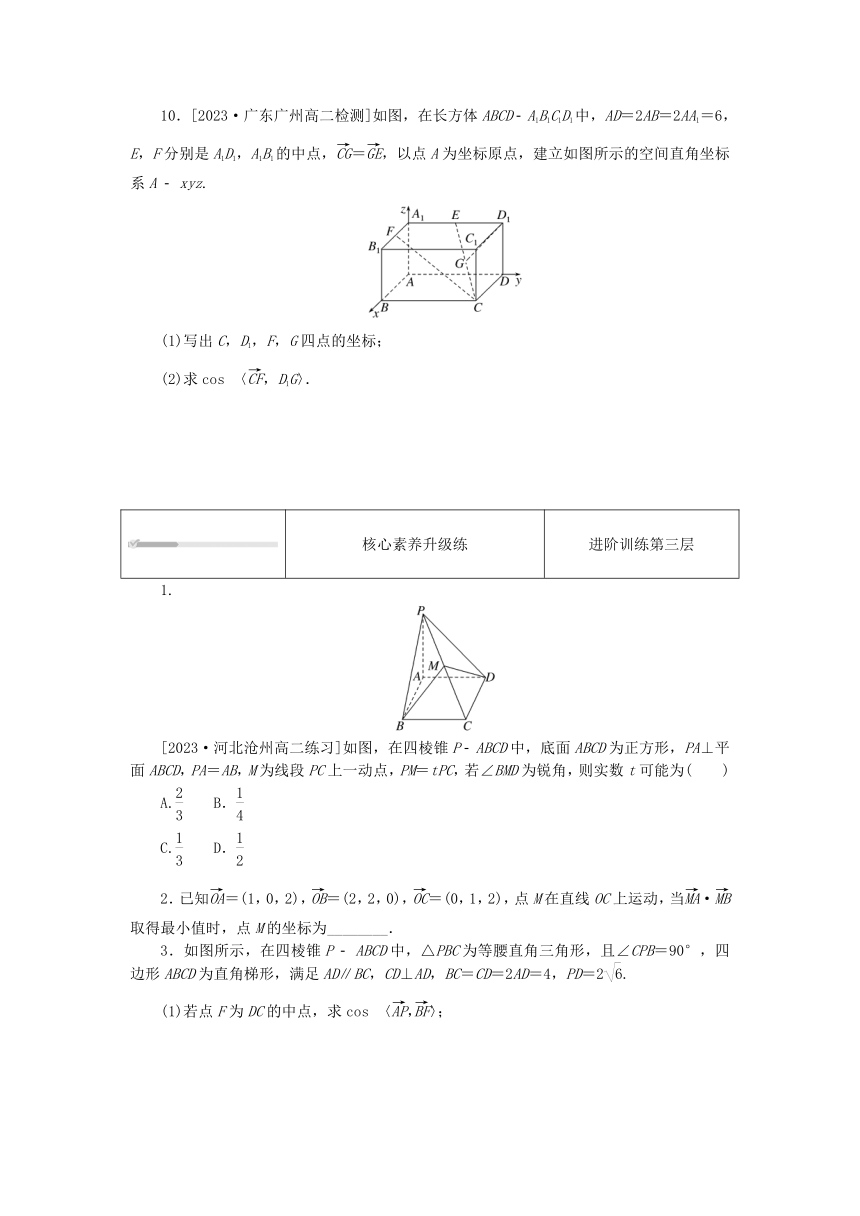
10.[2023·广东广州高二检测]如图,在长方体ABCD A1B1C1D1中,AD=2AB=2AA1=6,E,F分别是A1D1,A1B1的中点,=,以点A为坐标原点,建立如图所示的空间直角坐标系A xyz.
(1)写出C,D1,F,G四点的坐标;
(2)求cos 〈,D1G〉.
核心素养升级练 进阶训练第三层
1.
[2023·河北沧州高二练习]如图,在四棱锥P ABCD中,底面ABCD为正方形,PA⊥平面ABCD,PA=AB,M为线段PC上一动点,PM=tPC,若∠BMD为锐角,则实数t可能为( )
A. B.
C. D.
2.已知=(1,0,2),=(2,2,0),=(0,1,2),点M在直线OC上运动,当·取得最小值时,点M的坐标为________.
3.如图所示,在四棱锥P ABCD中,△PBC为等腰直角三角形,且∠CPB=90°,四边形ABCD为直角梯形,满足AD∥BC,CD⊥AD,BC=CD=2AD=4,PD=2.
(1)若点F为DC的中点,求cos 〈,〉;
(2)若点E为PB的中点,点M为AB上一点,当⊥时,求的值.
1.3 空间向量及其运算的坐标表示
必备知识基础练
1.答案:C
解析:点A(2,0,22)关于y轴的对称点的坐标为(-2,0,-22).故选C.
2.答案:B
解析:根据空间中点的坐标确定方法知,空间中点a=(1,2,-3)在坐标平面Oyz上的投影坐标,横坐标为0,纵坐标与竖坐标不变.所以空间向量a=(1,2,-3)在坐标平面Oyz上的投影向量是(0,2,-3).故选B.
3.答案:B
解析:由于向量a=(x,-2,6)与b=(1,y,-3)平行,注意到6=(-3)×(-2),所以,故x=-2,y=1,x+y=-1.故选B.
4.答案:A
解析:以A为坐标原点,,,正方向为x,y,z轴,可建立如图所示空间直角坐标系,则A(0,0,0),B1(1,0,3),C1(1,2,3),∴M(1,1,3),=(1,1,3),∴||==,即AM的长为.故选A.
5.答案:AC
解析:因为a=(1,-2,-2),b=(6,-3,2),所以a+b=(7,-5,0),故A正确;a-b=(-5,1,-4),故B不正确;a·b=1×6+2×3-2×2=8,故C正确;|a|==3,故D不正确.故选AC.
6.答案:BC
解析:因为点C关于平面Oxy对称的点为(-1,3,-1),所以A错误;因为||==,所以B正确;因为=(-1,2,1),=(1,-2,-1),则=-,所以C正确;因为=(0,1,0),=(1,-2,-1),则·=-2≠0,所以D错误.故选BC.
7.答案:
解析:因为=(3,2,1),=(1,0,5),点M为线段AB的中点,所以=(+)=(2,1,3),所以=-=(3,-1,4),所以||==.
8.答案:0.4
解析:如图,以D为坐标原点建立空间直角坐标系,设AD=2,则A(2,0,0),C(0,2,0),M(2,2,1),N(1,2,2),∴=(0,2,1),=(1,0,2),则cos 〈,〉==,故直线AM和CN所成角的余弦值为.
关键能力综合练
1.答案:C
解析:由b⊥c,b⊥a得b·c=2-4y+2=0 y=1,b·a=x+y+1=x+2=0 x=-2,故cos 〈a,c〉===-,∵〈a,c〉∈[0,π],故a,c的夹角为.故选C.
2.答案:B
解析:a=(1,2,-y),b=(x,1,2),且2b∥(a-b),则2b=(2x,2,4),a-b=(1-x,1,-y-2),因为2b∥(a-b),∴2b=λ(a-b),即,解得.故选B.
3.答案:A
解析:以点A为坐标原点,AB,AD,AA′所在直线分别为x、y、z建立空间直角坐标系,则A(0,0,0),B(a,0,0),C(a,a,0),D(0,a,0),A′(0,0,a),B′(a,0,a),C′(a,a,a),D′(0,a,a),O(,,).对于A选项,=(a,0,0),=(a,a,0),·=a2,A对;对于B选项,=,·=a2,B错;对于C选项,=(,,),·=a2,C错;对于D选项,=(0,a,0),=(0,-a,a),·=-a2,D错.故选A.
4.答案:BD
解析:由题得2a+b=(-1,2,7),a=(-2,-1,1),而≠≠,故A不正确;因为|a|=,|b|=5,所以5|a|=|b|,故B正确;因为a·(5a+4b)=(-2,-1,1)·(2,11,25)=10≠0,故C不正确;因为a在b上的投影数量为|a|cos 〈a,b〉===-,故D正确;故选BD.
5.答案:ABC
解析:=(-1,-1,3),则||==,故A正确;=(-2,2,0),则·=2-2+0=0,所以AB⊥AC,故B正确;=(-1,3,-3),=(1,1,-3),则cos ∠ABC===,故C正确;因为=(-1,-1,3),=(-2,2,0),≠,所以向量,不共线,则A,B,C三点不共线,故D错误.故选ABC.
6.答案:4
解析:根据a⊥b可得a·b=3+2x+1=0,故x=-2,此时b=(1,-2,1),由a∥c可得==,故y=6,此时c=(6,4,2),于是c-2b=(4,8,0),故|c-2b|=|(4,8,0)|==4.
7.答案:
解析:cos 〈a,b〉====0,故a⊥b,故以a,b为邻边的平行四边形为矩形,面积为|a|·|b|=·=.
8.答案:k<-1
解析:因为a=(1,1,0),b=(m,0,2),cos 〈a,b〉=-,所以cos 〈a,b〉===-,解得m=-1,所以b=(-1,0,2),所以a+kb=(1-k,1,2k),2a+b=(1,2,2),因为向量a+kb与2a+b所成角为钝角,所以(a+kb)·(2a+b)=1-k+2+4k<0,解得k<-1,若向量a+kb与2a+b共线,则==,解得k=,此时a+b与2a+b共线同向,综上可得k<-1.
9.解析:(1)a+b=(-1,0,c)+(1,1,0)=(0,1,c),
所以|a+b|==,解得:c=±2.
(2)当c=2时,ka+b=(k,k,0)+(-1,0,2)=(k-1,k,2),
2a-b=(2,2,0)-(-1,0,2)=(3,2,-2),
因为ka+b与2a-b互相垂直,
所以3(k-1)+2k-22=0,解得:k=,
当c=-2时,ka+b=(k,k,0)+(-1,0,-2)=(k-1,k,-2),
2a-b=(2,2,0)-(-1,0,-2)=(3,2,2),
因为ka+b与2a-b互相垂直,
所以3(k-1)+2k-22=0,解得:k=,
综上:k=.
10.解析:(1)∵AD=2AB=2AA1=6,∴AB=AA1=3,
则C(3,6,0),D1(0,6,3),F(,0,3),E(0,3,3),
∵=,∴G为CE中点,∴G(,,).
(2)由(1)得:=(-,-6,3),
=(,-,-),
===.
核心素养升级练
1.答案:B
解析:
分别以AB、AD、AP为x轴,y轴,z轴建立空间直角坐标系,如图所示.设PA=1,M(x,y,z),故P(0,0,1),C(1,1,0),=(x,y,z-1),=(1,1,-1),由=t(0≤t≤1)可知,即M(t,t,1-t),又因为∠BMD为锐角,所以·>0,由B(1,0,0),D(0,1,0),可知=(1-t,-t,t-1),=(-t,1-t,t-1),·=-t(1-t)-t(1-t)+(t-1)2>0,整理得3t2-4t+1>0,解得0≤t<.故选B.
2.答案:M(0,,)
解析:设M(x,y,z),∵点M在直线OC上运动,∴存在实数λ,使得=λ,∴(x,y,z)=λ(0,1,2),得到x=0,y=λ,z=2λ.·=(1,-λ,2-2λ)(2,2-λ,-2λ)=2-λ(2-λ)-2λ(2-2λ)=2-2λ+λ2-4λ+4λ2=5λ2-6λ+2=52+.当且仅当λ=时,·取得最小值,此时M(0,,).
3.解析:(1)因为△PBC为等腰直角三角形,∠CPB=90°,BC=CD=4,所以PC=PB=2,
又PD2=(2)2=24,PC2+CD2=(2)2+42=24,所以DC⊥PC.
而CD⊥AD,CD∥BC,故CD⊥BC,
因PC∩BC=C,PC,BC 平面PBC,故CD⊥平面PBC.
以点C为原点,CP,CD所在直线分别为x,z轴,过点C作PB的平行线为y轴,建立空间直角坐标系C xyz,如图所示.
则P(2,0,0),B(2,2,0),F(0,0,2),A(,,4),
则=(,-,-4),=(-2,-2,2),
所以cos 〈,〉=
==-.
(2)由(1)知E(2,,0),设=t,
而=(,,-4),所以=(t,t,-4t),
所以M(+t,+t,4-4t),
所以=(t-,t,4-4t),
又=(-2,-2,2),
因为⊥,故·=0,
所以-2×(t-)-2×t+8-8t=0,
解得t=,所以=.
必备知识基础练 进阶训练第一层
1.点A(2,0,22)关于y轴的对称点的坐标为( )
A.(-2,0,22) B.(2,0,-22)
C.(-2,0,-22) D.(2,0,22)
2.已知空间向量a=(1,2,-3),则向量a在坐标平面Oyz上的投影向量是( )
A.(0,2,3) B.(0,2,-3)
C.(1,2,0) D.(1,2,-3)
3.[2023·山东潍坊高二检测]已知向量a=(x,-2,6)与b=(1,y,-3)平行,则x+y=( )
A.1 B.-1
C.3 D.-3
4.在长方体ABCD A1B1C1D1中,已知AB=1,AD=2,AA1=3,M为B1C1的中点,则AM的长等于( )
A. B.
C.3 D.
5.(多选)已知向量a=(1,-2,-2),b=(6,-3,2),则下列结论正确的是( )
A.a+b=(7,-5,0) B.a-b=(5,-1,4)
C.a·b=8 D.|a|=
6.[2023·山东济南历城二中高二检测](多选)已知空间中三点A(0,1,0),B(1,-2,-1),C(-1,3,1),O是坐标原点,下列说法正确的是( )
A.点C关于平面Oxy对称的点为(1,-3,1)
B.||=
C.∥
D.⊥
7.[2023·山东德州高二检测]在空间直角坐标系中,已知=(3,2,1),=(1,0,5),=(-1,2,-1),点M为线段AB的中点,则||=________.
8.正方体ABCD A1B1C1D1中,M,N分别为棱BB1和B1C1的中点,则直线AM和CN所成角的余弦值为________.
关键能力综合练 进阶训练第二层
1.[2023·福建三明高二检测]向量a=(x,1,1),b=(1,y,1),c=(2,-4,2),且b⊥c,b⊥a,则a,c的夹角大小为( )
A. B.
C. D.
2.已知a=(1,2,-y),b=(x,1,2),且2b∥(a-b),则( )
A.x=,y=1 B.x=,y=-4
C.x=2,y= D.x=1,y=-1
3.已知正方体ABCD A′B′C′D′的棱长为a,对角线AC′与BD′相交于点O,则有( )
A.·=a2 B.·=a2
C.·=a D.·=a2
4.[2023·安徽泗县一中高二检测](多选)已知空间向量a=(-2,-1,1),b=(3,4,5),则下列结论正确的是( )
A.(2a+b)∥a
B.5|a|=|b|
C.a⊥(5a+4b)
D.a在b上的投影数量为-
5.[2023·山东青岛二中高二检测](多选)已知空间中三点A(2,1,-1),B(1,0,2),C(0,3,-1),则( )
A.||= B.AB⊥AC
C.cos ∠ABC= D.A,B,C三点共线
6.设x,y∈R,向量a=(3,2,1),b=(1,x,1),c=(y,4,2),且a⊥b,a∥c,则|c-2b|=________.
7.已知向量a=(2,-1,1),b=(1,3,1),则以a,b为邻边的平行四边形的面积为________.
8.已知向量a=(1,1,0),b=(m,0,2),cos 〈a,b〉=-,若向量a+kb与2a+b所成角为钝角,则实数k的范围是________.
9.[2023·山东潍坊高二检测]已知向量a=(1,1,0),b=(-1,0,c),且|a+b|=.
(1)求c的值;
(2)若ka+b与2a-b互相垂直,求实数k的值.
10.[2023·广东广州高二检测]如图,在长方体ABCD A1B1C1D1中,AD=2AB=2AA1=6,E,F分别是A1D1,A1B1的中点,=,以点A为坐标原点,建立如图所示的空间直角坐标系A xyz.
(1)写出C,D1,F,G四点的坐标;
(2)求cos 〈,D1G〉.
核心素养升级练 进阶训练第三层
1.
[2023·河北沧州高二练习]如图,在四棱锥P ABCD中,底面ABCD为正方形,PA⊥平面ABCD,PA=AB,M为线段PC上一动点,PM=tPC,若∠BMD为锐角,则实数t可能为( )
A. B.
C. D.
2.已知=(1,0,2),=(2,2,0),=(0,1,2),点M在直线OC上运动,当·取得最小值时,点M的坐标为________.
3.如图所示,在四棱锥P ABCD中,△PBC为等腰直角三角形,且∠CPB=90°,四边形ABCD为直角梯形,满足AD∥BC,CD⊥AD,BC=CD=2AD=4,PD=2.
(1)若点F为DC的中点,求cos 〈,〉;
(2)若点E为PB的中点,点M为AB上一点,当⊥时,求的值.
1.3 空间向量及其运算的坐标表示
必备知识基础练
1.答案:C
解析:点A(2,0,22)关于y轴的对称点的坐标为(-2,0,-22).故选C.
2.答案:B
解析:根据空间中点的坐标确定方法知,空间中点a=(1,2,-3)在坐标平面Oyz上的投影坐标,横坐标为0,纵坐标与竖坐标不变.所以空间向量a=(1,2,-3)在坐标平面Oyz上的投影向量是(0,2,-3).故选B.
3.答案:B
解析:由于向量a=(x,-2,6)与b=(1,y,-3)平行,注意到6=(-3)×(-2),所以,故x=-2,y=1,x+y=-1.故选B.
4.答案:A
解析:以A为坐标原点,,,正方向为x,y,z轴,可建立如图所示空间直角坐标系,则A(0,0,0),B1(1,0,3),C1(1,2,3),∴M(1,1,3),=(1,1,3),∴||==,即AM的长为.故选A.
5.答案:AC
解析:因为a=(1,-2,-2),b=(6,-3,2),所以a+b=(7,-5,0),故A正确;a-b=(-5,1,-4),故B不正确;a·b=1×6+2×3-2×2=8,故C正确;|a|==3,故D不正确.故选AC.
6.答案:BC
解析:因为点C关于平面Oxy对称的点为(-1,3,-1),所以A错误;因为||==,所以B正确;因为=(-1,2,1),=(1,-2,-1),则=-,所以C正确;因为=(0,1,0),=(1,-2,-1),则·=-2≠0,所以D错误.故选BC.
7.答案:
解析:因为=(3,2,1),=(1,0,5),点M为线段AB的中点,所以=(+)=(2,1,3),所以=-=(3,-1,4),所以||==.
8.答案:0.4
解析:如图,以D为坐标原点建立空间直角坐标系,设AD=2,则A(2,0,0),C(0,2,0),M(2,2,1),N(1,2,2),∴=(0,2,1),=(1,0,2),则cos 〈,〉==,故直线AM和CN所成角的余弦值为.
关键能力综合练
1.答案:C
解析:由b⊥c,b⊥a得b·c=2-4y+2=0 y=1,b·a=x+y+1=x+2=0 x=-2,故cos 〈a,c〉===-,∵〈a,c〉∈[0,π],故a,c的夹角为.故选C.
2.答案:B
解析:a=(1,2,-y),b=(x,1,2),且2b∥(a-b),则2b=(2x,2,4),a-b=(1-x,1,-y-2),因为2b∥(a-b),∴2b=λ(a-b),即,解得.故选B.
3.答案:A
解析:以点A为坐标原点,AB,AD,AA′所在直线分别为x、y、z建立空间直角坐标系,则A(0,0,0),B(a,0,0),C(a,a,0),D(0,a,0),A′(0,0,a),B′(a,0,a),C′(a,a,a),D′(0,a,a),O(,,).对于A选项,=(a,0,0),=(a,a,0),·=a2,A对;对于B选项,=,·=a2,B错;对于C选项,=(,,),·=a2,C错;对于D选项,=(0,a,0),=(0,-a,a),·=-a2,D错.故选A.
4.答案:BD
解析:由题得2a+b=(-1,2,7),a=(-2,-1,1),而≠≠,故A不正确;因为|a|=,|b|=5,所以5|a|=|b|,故B正确;因为a·(5a+4b)=(-2,-1,1)·(2,11,25)=10≠0,故C不正确;因为a在b上的投影数量为|a|cos 〈a,b〉===-,故D正确;故选BD.
5.答案:ABC
解析:=(-1,-1,3),则||==,故A正确;=(-2,2,0),则·=2-2+0=0,所以AB⊥AC,故B正确;=(-1,3,-3),=(1,1,-3),则cos ∠ABC===,故C正确;因为=(-1,-1,3),=(-2,2,0),≠,所以向量,不共线,则A,B,C三点不共线,故D错误.故选ABC.
6.答案:4
解析:根据a⊥b可得a·b=3+2x+1=0,故x=-2,此时b=(1,-2,1),由a∥c可得==,故y=6,此时c=(6,4,2),于是c-2b=(4,8,0),故|c-2b|=|(4,8,0)|==4.
7.答案:
解析:cos 〈a,b〉====0,故a⊥b,故以a,b为邻边的平行四边形为矩形,面积为|a|·|b|=·=.
8.答案:k<-1
解析:因为a=(1,1,0),b=(m,0,2),cos 〈a,b〉=-,所以cos 〈a,b〉===-,解得m=-1,所以b=(-1,0,2),所以a+kb=(1-k,1,2k),2a+b=(1,2,2),因为向量a+kb与2a+b所成角为钝角,所以(a+kb)·(2a+b)=1-k+2+4k<0,解得k<-1,若向量a+kb与2a+b共线,则==,解得k=,此时a+b与2a+b共线同向,综上可得k<-1.
9.解析:(1)a+b=(-1,0,c)+(1,1,0)=(0,1,c),
所以|a+b|==,解得:c=±2.
(2)当c=2时,ka+b=(k,k,0)+(-1,0,2)=(k-1,k,2),
2a-b=(2,2,0)-(-1,0,2)=(3,2,-2),
因为ka+b与2a-b互相垂直,
所以3(k-1)+2k-22=0,解得:k=,
当c=-2时,ka+b=(k,k,0)+(-1,0,-2)=(k-1,k,-2),
2a-b=(2,2,0)-(-1,0,-2)=(3,2,2),
因为ka+b与2a-b互相垂直,
所以3(k-1)+2k-22=0,解得:k=,
综上:k=.
10.解析:(1)∵AD=2AB=2AA1=6,∴AB=AA1=3,
则C(3,6,0),D1(0,6,3),F(,0,3),E(0,3,3),
∵=,∴G为CE中点,∴G(,,).
(2)由(1)得:=(-,-6,3),
=(,-,-),
===.
核心素养升级练
1.答案:B
解析:
分别以AB、AD、AP为x轴,y轴,z轴建立空间直角坐标系,如图所示.设PA=1,M(x,y,z),故P(0,0,1),C(1,1,0),=(x,y,z-1),=(1,1,-1),由=t(0≤t≤1)可知,即M(t,t,1-t),又因为∠BMD为锐角,所以·>0,由B(1,0,0),D(0,1,0),可知=(1-t,-t,t-1),=(-t,1-t,t-1),·=-t(1-t)-t(1-t)+(t-1)2>0,整理得3t2-4t+1>0,解得0≤t<.故选B.
2.答案:M(0,,)
解析:设M(x,y,z),∵点M在直线OC上运动,∴存在实数λ,使得=λ,∴(x,y,z)=λ(0,1,2),得到x=0,y=λ,z=2λ.·=(1,-λ,2-2λ)(2,2-λ,-2λ)=2-λ(2-λ)-2λ(2-2λ)=2-2λ+λ2-4λ+4λ2=5λ2-6λ+2=52+.当且仅当λ=时,·取得最小值,此时M(0,,).
3.解析:(1)因为△PBC为等腰直角三角形,∠CPB=90°,BC=CD=4,所以PC=PB=2,
又PD2=(2)2=24,PC2+CD2=(2)2+42=24,所以DC⊥PC.
而CD⊥AD,CD∥BC,故CD⊥BC,
因PC∩BC=C,PC,BC 平面PBC,故CD⊥平面PBC.
以点C为原点,CP,CD所在直线分别为x,z轴,过点C作PB的平行线为y轴,建立空间直角坐标系C xyz,如图所示.
则P(2,0,0),B(2,2,0),F(0,0,2),A(,,4),
则=(,-,-4),=(-2,-2,2),
所以cos 〈,〉=
==-.
(2)由(1)知E(2,,0),设=t,
而=(,,-4),所以=(t,t,-4t),
所以M(+t,+t,4-4t),
所以=(t-,t,4-4t),
又=(-2,-2,2),
因为⊥,故·=0,
所以-2×(t-)-2×t+8-8t=0,
解得t=,所以=.
