2023版新教材高中数学单元素养测评卷一第一章 空间向量与立体几何(含解析)
文档属性
| 名称 | 2023版新教材高中数学单元素养测评卷一第一章 空间向量与立体几何(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 414.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-11 10:06:50 | ||
图片预览




文档简介
单元素养测评卷(一) 空间向量与立体几何
时间:120分钟 满分:150分
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.若直线l的方向向量为a=(1,0,2),平面α的法向量为n=(-2,1,1),则( )
A.l∥α B.l⊥α C.l α或l∥α D.l与α斜交
2.若直线l的方向向量与平面α的法向量的夹角等于130°,则直线l与平面α所成的角等于( )
A.130° B.60° C.40° D.50°
3.A,B,C三点不共线,对空间内任意一点O,若=++,则P,A,B,C四点( )
A.一定不共面 B.一定共面 C.不一定共面 D.无法判断是否共面
4.已知A(2,0,0),B(0,2,0),C(0,0,2),则平面ABC的一个单位法向量是( )
A.(1,1,1) B.(,,) C.(,,) D.(,-,)
5.在四棱锥P ABCD中,=(4,-2,3),=(-4,1,0),=(-6,2,-8),则这个四棱锥的高h等于( )
A.1 B.2 C.13 D.26
6.已知向量a=(4,-2,6),b=(-2,1,x),则使a⊥b,a∥b成立的x分别为( )
A.,-3 B.,-3 C.,3 D.,3
7.
如图所示,E,F分别是四面体OABC的棱OA,BC的中点,D是线段EF的一个四等分点(靠近E点),设=a,=b,=c,则=( )
A.a+b+c B.a+b+c
C.a+b+c D.a+b+c
8.在矩形ABCD中,AB=1,BC=,PA⊥平面ABCD,PA=1,则PC与平面ABCD所成的角为( )
A.30° B.45° C.60° D.120°
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.关于点P(1,-1,2),下列说法正确的是( )
A.点P关于Oxy平面的对称点P1的坐标为(1,-1,-2)
B.点P关于x轴的对称点P2的坐标为(-1,-1,2)
C.点P关于Oyz平面的对称点P3的坐标为(-1,-1,2)
D.点P关于y轴的对称点P4的坐标为(-1,-1,-2)
10.下列关于空间向量的命题中,正确的有( )
A.若非零向量a,b,c满足a⊥b,b⊥c,则有a∥c
B.若向量a,b与空间任意向量都不能构成基底,则a∥b
C.空间向量a=(-2,-1,1),b=(3,4,5)夹角的余弦值为-
D.已知a=(-1,1,2),b=(0,2,3),若ka+b与2a-b垂直,则k=-
11.已知v1,v2分别为直线l1,l2的方向向量(l1,l2不重合),n1,n2分别为平面α,β的法向量(α,β不重合),则下列说法正确的是( )
A.v1∥v2 l1⊥l2 B.v1⊥v2 l1⊥l2 C.n1∥n2 α⊥β D.n1⊥n2 α⊥β
12.如图,已知正方体ABCD A1B1C1D1的棱长为2,E,F,G分别为AD,AB,B1C1的中点,以下说法正确的是( )
A.三棱锥C EFG的体积为1
B.A1C⊥平面EFG
C.过点E,F,G作正方体的截面,所得截面的面积是3
D.平面EGF与平面ABCD夹角的余弦值为
三、填空题:本题共4小题,每小题5分,共20分.
13.空间中任意四个点A,B,C,D,则+-+2=________.
14.已知直线l过定点A(3,2,1),且n=(1,0,1)为其一个方向向量,则点P(3,3,2)到直线l的距离为________.
15.已知向量a=(-2,1,1),点A(-3,-1,4),B(-2,-2,2).在直线AB上,存在一点E,使得⊥a,则点E的坐标为________.
16.在棱长为1的正方体ABCD A′B′C′D′中,已知点P是正方形AA′D′D内部(不含边界)的一个动点,若直线AP与平面AA′B′B所成角的正弦值和异面直线AP与DC′所成角的余弦值相等,则线段DP长度的最小值是________.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分10分)已知:a=(x,4,1),b=(-2,y,-1),c=(3,-2,z),a∥b,b⊥c,求:
(1)a,b,c;
(2)a+c与b+c所成角的余弦值.
18.(本小题满分12分)如图所示,在四棱锥M-ABCD中,底面ABCD是边长为2的正方形,侧棱AM的长为3,且AM和AB,AD的夹角都是60°,N是CM的中点,设a=,b=,c=,试以a,b,c为基向量表示出向量,并求BN的长.
19.(本小题满分12分)在如图所示的平行六面体(底面是平行四边形的四棱柱)ABCD A1B1C1D1中,AB=AD=AA1=1,∠BAD=∠BAA1=∠DAA1=60°.
(1)证明:AC1⊥平面A1BD;
(2)若O是AC1的中点,求AO长.
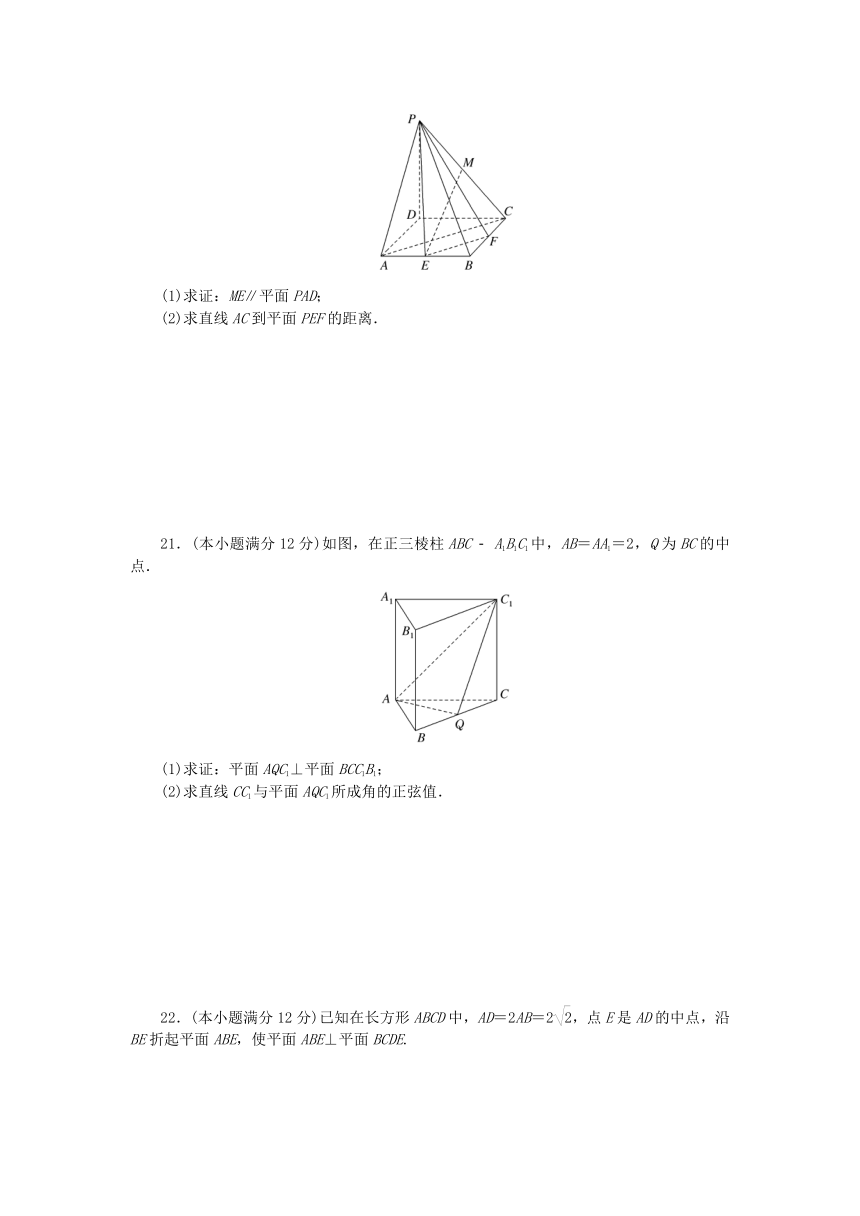
20.(本小题满分12分)如图,已知正方形ABCD的边长为1,PD⊥平面ABCD,且PD=1,M,E,F分别为PC,AB,BC的中点.
(1)求证:ME∥平面PAD;
(2)求直线AC到平面PEF的距离.
21.(本小题满分12分)如图,在正三棱柱ABC A1B1C1中,AB=AA1=2,Q为BC的中点.
(1)求证:平面AQC1⊥平面BCC1B1;
(2)求直线CC1与平面AQC1所成角的正弦值.
22.(本小题满分12分)已知在长方形ABCD中,AD=2AB=2,点E是AD的中点,沿BE折起平面ABE,使平面ABE⊥平面BCDE.
(1)求证:在四棱锥A BCDE中,AB⊥AC;
(2)在线段AC上是否存在点F,使二面角A BE F的余弦值为?若存在,找出点F的位置;若不存在,请说明理由.
单元素养测评卷(一)
1.答案:C
解析:∵a=(1,0,2),n=(-2,1,1),
∴a·n=0,即a⊥n,∴l∥α或l α.故选C.
2.答案:C
解析:因为直线l的方向向量与平面α的法向量的夹角等于130°,
所以它们所在直线的夹角为50°,
则直线l与平面α所成的角等于90°-50°=40°.故选C.
3.答案:B
解析:因为=++,
则-=-++,
即-=-)+(-),
即=+.
由空间向量共面定理可知,,,共面,则P,A,B,C四点一定共面.故选B.
4.答案:B
解析:因为A(2,0,0),B(0,2,0),C(0,0,2),
所以=(-2,2,0),=(-2,0,2).
令平面ABC的一个法向量为n=(x,y,z),
可得,即,令x=1,则y=z=1,所以n=(1,1,1),
故平面ABC的单位法向量是±,即(,,)或(-,-,-).故选B.
5.答案:B
解析:设平面ABCD的法向量为n=(x,y,z),
则即
不妨令x=3,则y=12,z=4,
可得n=(3,12,4),
四棱锥的高h===2.
6.答案:A
解析:当a⊥b时,a·b=4×(-2)-2×1+6x=-10+6x=0,解得x=;
当a∥b时,则有==,解得x=-3.故选A.
7.答案:C
解析:如图所示,连接OF,
=+=+=+(-)
=+[(+)-]=++=a+b+c.故选C.
8.答案:A
解析:以点A为坐标原点,AD,AB,AP所在的直线分别为x轴,y轴,z轴,建立空间直角坐标系,
则P(0,0,1),C(,1,0),=(,1,-1),
平面ABCD的一个法向量为n=(0,0,1),
所以cos 〈,n〉==-.
又因为〈,n〉∈[0,π],所以〈,n〉=120°,
所以斜线PC与平面ABCD的法向量所在的直线所成的角为60°,
所以斜线PC与平面ABCD所成的角为30°.
9.答案:ACD
解析:求点关于坐标轴或坐标平面对称的点的坐标,其规律是“关于谁对称,谁不变”,如点(x,y,z)关于y轴的对称点为(-x,y,-z),关于平面Oyz的对称点是(-x,y,z),点(x,y,z)关于x轴的对称点为(x,-y,-z),关于平面Oxy的对称点是(x,y,-z),
故A选项点P关于Oxy平面的对称点P1的坐标为(1,-1,-2),故A正确;B选项点P关于x轴的对称点P2的坐标为(1,1,-2),故B错误;
C选项点P关于Oyz平面的对称点P3的坐标为(-1,-1,2),故C正确;
D选项点P关于y轴的对称点P4的坐标为(-1,-1,-2),故D正确.故选ACD.
10.答案:BCD
解析:对于A,若非零向量a,b,c满足a⊥b,b⊥c,则a与c的位置关系不确定,也有可能平行,故A错误;
对于B,若向量a,b与空间任意向量都不能构成基底,则只能两个向量是共线向量,故a∥b,故B正确;
对于C,因为a=(-2,-1,1),b=(3,4,5),所以|a|==,|b|==5,a·b=-2×3-1×4+1×5=-5,设a与b的夹角为θ,则cos θ===-,故C正确;
对于D:因为a=(-1,1,2),b=(0,2,3),所以ka+b=k(-1,1,2)+(0,2,3)=(-k,k+2,2k+3),2a-b=2(-1,1,2)-(0,2,3)=(-2,0,1),因为ka+b与2a-b垂直,所以(ka+b)·(2a-b)=0,即-k×(-2)+0×(k+2)+1×(2k+3)=0,解得k=-,故D正确.故选BCD.
11.答案:BD
解析:因为v1,v2分别为直线l1,l2的方向向量(l1,l2不重合),
则v1∥v2 l1∥l2,故选项A错误;
则v1⊥v2 l1⊥l2,故选项B正确;
因为n1,n2分别为平面α,β的法向量(α,β不重合),
则n1∥n2 α∥β,故选项C错误;
则n1⊥n2 α⊥β,故选项D正确.故选BD.
12.答案:ABC
解析:对于A,VC EFG=·S△ECF·CC1=××2=1,故A正确;
对于B,以DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,C(0,2,0),A1(2,0,2),E(1,0,0),F(2,1,0),G(1,2,2),
则=(-2,2,-2),=(1,1,0),=(0,2,2),·=0,·=0,
则A1C⊥平面EFG,B正确;
对于C,作C1D1的中点N,BB1的中点M,DD1的中点T,连接GN,GM,FM,TN,ET,则正六边形EFMGNT为对应截面面积,正六边形边长为,则截面面积为S=6××()2=3,故C正确;
对于D,平面ABCD的一个法向量为n=(0,0,1),
平面EGF的一个法向量为=(-2,2,-2),设两个平面夹角为θ,
cos θ===,故D错误.故选ABC.
13.答案:
解析:+-+2=++2=-+2=+2=.
14.答案:
解析:设a==(0,1,1),u==(,0,),则a·u=,
则点P到直线l的距离d== =.
15.答案:(-,-,)
解析:设=λ,因为A(-3,-1,4),B(-2,-2,2),所以=(1,-1,-2),=(λ,-λ,-2λ),=(3,1,-4),=-=(λ-3,-λ-1,-2λ+4),
因为⊥a,所以-2(λ-3)+(-λ-1)+(-2λ+4)=0,解得λ=,又A(-3,-1,4),=(λ,-λ,-2λ),所以点E的坐标为(-,-,).
16.答案:
解析:如图,以D为坐标原点,DA,DC,DD′所在直线为x,y,z轴建立空间直角坐标系,
设P(x,0,z),0=(x-1,0,z),=(0,1,1),=(1,0,0),
设直线AP与平面AA′B′B所成角为θ和异面直线AP与DC′所成角为α,
可得cos α=cos 〈,〉=,
sin θ=|cos 〈,〉|=,0由sin θ=cos α,可得z=(1-x),
则||==
= ,
当x=时,线段DP长度的最小值为.
17.解析:(1)∵a∥b,∴==,解得x=2,y=-4,
故a=(2,4,1),b=(-2,-4,-1).
又因为b⊥c,所以b·c=0,即-6+8-z=0,解得z=2,
故c=(3,-2,2).
(2)由(1)可得a+c=(5,2,3),b+c=(1,-6,1),
设向量a+c与b+c所成的角为θ,|a+c|=,|b+c|=,
(a+c)·(b+c)=5-12+3=-4,
则cos θ==-.
18.解析:=+=+
=+(-)
=+[-(+)]
=-++.
所以=-a+b+c,
||2=2=
=(a2+b2+c2-2a·b-2a·c+2b·c)
=.
所以||=,即BN的长为.
19.解析:(1)证明:连接BD和A1B,由于=++,=-,=-,
∴·=·(-)=0,
∴⊥BD,
同理·=0,AC1⊥A1B,
且BD∩A1B=B,
所以AC1⊥平面A1BD.
(2)||2=(++)2=2+2+2+2·+2·+2·
=1+1+1+3×2×1×1×cos 60°=6.
∴||=.
∴||=||=.
20.解析:(1)证明:取PD的中点N,连接MN和AN,则MN∥DC且MN=DC,
又底面ABCD为正方形,∴MN∥AE且MN=AE=AB,
∴四边形MNAE为平行四边形,∴AN∥ME,
又AN 平面PAD,ME 平面PAD,
∴ME∥平面PAD.
(2)建立以D为坐标原点,,,分别为x轴,y轴,z轴正方向的空间直角坐标系,如图所示.
则P(0,0,1),A(1,0,0),C(0,1,0),E(1,,0),F(,1,0),所以=(-,,0),=(1,,-1),=(1,,0),设平面PEF的法向量为n=(x,y,z),则,即,
令x=2,则y=2,z=3,所以n=(2,2,3),
因为E,F分别为AB,BC的中点,所以EF∥AC.
又AC 平面PEF,EF 平面PEF,所以AC∥平面PEF;
因为=(0,,0),所以点A到平面PEF的距离d===.
所以直线AC到平面PEF的距离为.
21.解析:(1)证明:因为三棱柱ABC A1B1C1为正三棱柱,所以△ABC为正三角形,
因为Q为BC的中点,所以AQ⊥BC,
因为BB1⊥平面ABC,AQ 平面ABC,所以BB1⊥AQ,
因为BB1∩BC=B,BB1 平面BCC1B1,BC 平面BCC1B1,
所以AQ⊥平面BCC1B1,
又因为AQ 平面AQC1,所以平面AQC1⊥平面BCC1B1.
(2)设AC,A1C1的中点分别为O,O1,由三棱柱ABC A1B1C1为正三棱柱可知,
OB⊥OC,OB⊥OO1,OO1⊥OC,以{OB,OC,OO1}为基底建立空间直角坐标系O xyz.
因为AB=AA1=2,所以A(0,-1,0),B(,0,0),C(0,1,0),B1(,0,2),C1(0,1,2),
因为Q为BC的中点,所以Q(,,0),
所以=(,,0),=(0,2,2),=(0,0,2),
设n=(x,y,z)为平面AQC1的法向量,
所以直线CC1与平面AQC1所成角的正弦值为.
22.解析:(1)证明:连接CE,∵E为AD的中点,AD=2AB=2,∴AE=AB=,
∵ABCD为长方形,∴AB⊥AD,AD=BC=2,
在△ABE中,BE===2,
同理EC=2,∴BE2+EC2=BC2,∴CE⊥BE,
在折叠后的图形中:
∵平面ABE⊥平面BCDE,平面ABE∩平面BCDE=BE,CE⊥BE,∴CE⊥平面ABE,
又AB 平面ABE,∴CE⊥AB,
又∵AE⊥AB,CE 平面AEC,AE 平面AEC,CE∩AE=E,∴AB⊥平面AEC,
又AC 平面AEC,∴AB⊥AC.
(2)由(1)可知:△ABE,△BEC均为等腰直角三角形,过A点作底边BE的高,交BE于O点,以O为原点建立空间直角坐标系,如图所示:
则A(0,0,1),B(1,0,0),C(-1,2,0),E(-1,0,0),=(1,0,1),=(-1,2,-1),=(2,0,0),
易知平面ABE的一个法向量为m=(0,1,0),
假设在线段AC上存在点F,使二面角A BE F的余弦值为,
设=λ,则=+λ=(1-λ,2λ,1-λ),
设平面BEF的一个法向量为n=(x,y,z),∴,∴,
取y=1,则n=(0,1,),
cos 〈m,n〉==,∴λ=,
即当点F为线段AC靠近A的四等分点时,二面角A BE F的余弦值为.
时间:120分钟 满分:150分
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.若直线l的方向向量为a=(1,0,2),平面α的法向量为n=(-2,1,1),则( )
A.l∥α B.l⊥α C.l α或l∥α D.l与α斜交
2.若直线l的方向向量与平面α的法向量的夹角等于130°,则直线l与平面α所成的角等于( )
A.130° B.60° C.40° D.50°
3.A,B,C三点不共线,对空间内任意一点O,若=++,则P,A,B,C四点( )
A.一定不共面 B.一定共面 C.不一定共面 D.无法判断是否共面
4.已知A(2,0,0),B(0,2,0),C(0,0,2),则平面ABC的一个单位法向量是( )
A.(1,1,1) B.(,,) C.(,,) D.(,-,)
5.在四棱锥P ABCD中,=(4,-2,3),=(-4,1,0),=(-6,2,-8),则这个四棱锥的高h等于( )
A.1 B.2 C.13 D.26
6.已知向量a=(4,-2,6),b=(-2,1,x),则使a⊥b,a∥b成立的x分别为( )
A.,-3 B.,-3 C.,3 D.,3
7.
如图所示,E,F分别是四面体OABC的棱OA,BC的中点,D是线段EF的一个四等分点(靠近E点),设=a,=b,=c,则=( )
A.a+b+c B.a+b+c
C.a+b+c D.a+b+c
8.在矩形ABCD中,AB=1,BC=,PA⊥平面ABCD,PA=1,则PC与平面ABCD所成的角为( )
A.30° B.45° C.60° D.120°
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.关于点P(1,-1,2),下列说法正确的是( )
A.点P关于Oxy平面的对称点P1的坐标为(1,-1,-2)
B.点P关于x轴的对称点P2的坐标为(-1,-1,2)
C.点P关于Oyz平面的对称点P3的坐标为(-1,-1,2)
D.点P关于y轴的对称点P4的坐标为(-1,-1,-2)
10.下列关于空间向量的命题中,正确的有( )
A.若非零向量a,b,c满足a⊥b,b⊥c,则有a∥c
B.若向量a,b与空间任意向量都不能构成基底,则a∥b
C.空间向量a=(-2,-1,1),b=(3,4,5)夹角的余弦值为-
D.已知a=(-1,1,2),b=(0,2,3),若ka+b与2a-b垂直,则k=-
11.已知v1,v2分别为直线l1,l2的方向向量(l1,l2不重合),n1,n2分别为平面α,β的法向量(α,β不重合),则下列说法正确的是( )
A.v1∥v2 l1⊥l2 B.v1⊥v2 l1⊥l2 C.n1∥n2 α⊥β D.n1⊥n2 α⊥β
12.如图,已知正方体ABCD A1B1C1D1的棱长为2,E,F,G分别为AD,AB,B1C1的中点,以下说法正确的是( )
A.三棱锥C EFG的体积为1
B.A1C⊥平面EFG
C.过点E,F,G作正方体的截面,所得截面的面积是3
D.平面EGF与平面ABCD夹角的余弦值为
三、填空题:本题共4小题,每小题5分,共20分.
13.空间中任意四个点A,B,C,D,则+-+2=________.
14.已知直线l过定点A(3,2,1),且n=(1,0,1)为其一个方向向量,则点P(3,3,2)到直线l的距离为________.
15.已知向量a=(-2,1,1),点A(-3,-1,4),B(-2,-2,2).在直线AB上,存在一点E,使得⊥a,则点E的坐标为________.
16.在棱长为1的正方体ABCD A′B′C′D′中,已知点P是正方形AA′D′D内部(不含边界)的一个动点,若直线AP与平面AA′B′B所成角的正弦值和异面直线AP与DC′所成角的余弦值相等,则线段DP长度的最小值是________.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分10分)已知:a=(x,4,1),b=(-2,y,-1),c=(3,-2,z),a∥b,b⊥c,求:
(1)a,b,c;
(2)a+c与b+c所成角的余弦值.
18.(本小题满分12分)如图所示,在四棱锥M-ABCD中,底面ABCD是边长为2的正方形,侧棱AM的长为3,且AM和AB,AD的夹角都是60°,N是CM的中点,设a=,b=,c=,试以a,b,c为基向量表示出向量,并求BN的长.
19.(本小题满分12分)在如图所示的平行六面体(底面是平行四边形的四棱柱)ABCD A1B1C1D1中,AB=AD=AA1=1,∠BAD=∠BAA1=∠DAA1=60°.
(1)证明:AC1⊥平面A1BD;
(2)若O是AC1的中点,求AO长.
20.(本小题满分12分)如图,已知正方形ABCD的边长为1,PD⊥平面ABCD,且PD=1,M,E,F分别为PC,AB,BC的中点.
(1)求证:ME∥平面PAD;
(2)求直线AC到平面PEF的距离.
21.(本小题满分12分)如图,在正三棱柱ABC A1B1C1中,AB=AA1=2,Q为BC的中点.
(1)求证:平面AQC1⊥平面BCC1B1;
(2)求直线CC1与平面AQC1所成角的正弦值.
22.(本小题满分12分)已知在长方形ABCD中,AD=2AB=2,点E是AD的中点,沿BE折起平面ABE,使平面ABE⊥平面BCDE.
(1)求证:在四棱锥A BCDE中,AB⊥AC;
(2)在线段AC上是否存在点F,使二面角A BE F的余弦值为?若存在,找出点F的位置;若不存在,请说明理由.
单元素养测评卷(一)
1.答案:C
解析:∵a=(1,0,2),n=(-2,1,1),
∴a·n=0,即a⊥n,∴l∥α或l α.故选C.
2.答案:C
解析:因为直线l的方向向量与平面α的法向量的夹角等于130°,
所以它们所在直线的夹角为50°,
则直线l与平面α所成的角等于90°-50°=40°.故选C.
3.答案:B
解析:因为=++,
则-=-++,
即-=-)+(-),
即=+.
由空间向量共面定理可知,,,共面,则P,A,B,C四点一定共面.故选B.
4.答案:B
解析:因为A(2,0,0),B(0,2,0),C(0,0,2),
所以=(-2,2,0),=(-2,0,2).
令平面ABC的一个法向量为n=(x,y,z),
可得,即,令x=1,则y=z=1,所以n=(1,1,1),
故平面ABC的单位法向量是±,即(,,)或(-,-,-).故选B.
5.答案:B
解析:设平面ABCD的法向量为n=(x,y,z),
则即
不妨令x=3,则y=12,z=4,
可得n=(3,12,4),
四棱锥的高h===2.
6.答案:A
解析:当a⊥b时,a·b=4×(-2)-2×1+6x=-10+6x=0,解得x=;
当a∥b时,则有==,解得x=-3.故选A.
7.答案:C
解析:如图所示,连接OF,
=+=+=+(-)
=+[(+)-]=++=a+b+c.故选C.
8.答案:A
解析:以点A为坐标原点,AD,AB,AP所在的直线分别为x轴,y轴,z轴,建立空间直角坐标系,
则P(0,0,1),C(,1,0),=(,1,-1),
平面ABCD的一个法向量为n=(0,0,1),
所以cos 〈,n〉==-.
又因为〈,n〉∈[0,π],所以〈,n〉=120°,
所以斜线PC与平面ABCD的法向量所在的直线所成的角为60°,
所以斜线PC与平面ABCD所成的角为30°.
9.答案:ACD
解析:求点关于坐标轴或坐标平面对称的点的坐标,其规律是“关于谁对称,谁不变”,如点(x,y,z)关于y轴的对称点为(-x,y,-z),关于平面Oyz的对称点是(-x,y,z),点(x,y,z)关于x轴的对称点为(x,-y,-z),关于平面Oxy的对称点是(x,y,-z),
故A选项点P关于Oxy平面的对称点P1的坐标为(1,-1,-2),故A正确;B选项点P关于x轴的对称点P2的坐标为(1,1,-2),故B错误;
C选项点P关于Oyz平面的对称点P3的坐标为(-1,-1,2),故C正确;
D选项点P关于y轴的对称点P4的坐标为(-1,-1,-2),故D正确.故选ACD.
10.答案:BCD
解析:对于A,若非零向量a,b,c满足a⊥b,b⊥c,则a与c的位置关系不确定,也有可能平行,故A错误;
对于B,若向量a,b与空间任意向量都不能构成基底,则只能两个向量是共线向量,故a∥b,故B正确;
对于C,因为a=(-2,-1,1),b=(3,4,5),所以|a|==,|b|==5,a·b=-2×3-1×4+1×5=-5,设a与b的夹角为θ,则cos θ===-,故C正确;
对于D:因为a=(-1,1,2),b=(0,2,3),所以ka+b=k(-1,1,2)+(0,2,3)=(-k,k+2,2k+3),2a-b=2(-1,1,2)-(0,2,3)=(-2,0,1),因为ka+b与2a-b垂直,所以(ka+b)·(2a-b)=0,即-k×(-2)+0×(k+2)+1×(2k+3)=0,解得k=-,故D正确.故选BCD.
11.答案:BD
解析:因为v1,v2分别为直线l1,l2的方向向量(l1,l2不重合),
则v1∥v2 l1∥l2,故选项A错误;
则v1⊥v2 l1⊥l2,故选项B正确;
因为n1,n2分别为平面α,β的法向量(α,β不重合),
则n1∥n2 α∥β,故选项C错误;
则n1⊥n2 α⊥β,故选项D正确.故选BD.
12.答案:ABC
解析:对于A,VC EFG=·S△ECF·CC1=××2=1,故A正确;
对于B,以DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,C(0,2,0),A1(2,0,2),E(1,0,0),F(2,1,0),G(1,2,2),
则=(-2,2,-2),=(1,1,0),=(0,2,2),·=0,·=0,
则A1C⊥平面EFG,B正确;
对于C,作C1D1的中点N,BB1的中点M,DD1的中点T,连接GN,GM,FM,TN,ET,则正六边形EFMGNT为对应截面面积,正六边形边长为,则截面面积为S=6××()2=3,故C正确;
对于D,平面ABCD的一个法向量为n=(0,0,1),
平面EGF的一个法向量为=(-2,2,-2),设两个平面夹角为θ,
cos θ===,故D错误.故选ABC.
13.答案:
解析:+-+2=++2=-+2=+2=.
14.答案:
解析:设a==(0,1,1),u==(,0,),则a·u=,
则点P到直线l的距离d== =.
15.答案:(-,-,)
解析:设=λ,因为A(-3,-1,4),B(-2,-2,2),所以=(1,-1,-2),=(λ,-λ,-2λ),=(3,1,-4),=-=(λ-3,-λ-1,-2λ+4),
因为⊥a,所以-2(λ-3)+(-λ-1)+(-2λ+4)=0,解得λ=,又A(-3,-1,4),=(λ,-λ,-2λ),所以点E的坐标为(-,-,).
16.答案:
解析:如图,以D为坐标原点,DA,DC,DD′所在直线为x,y,z轴建立空间直角坐标系,
设P(x,0,z),0
设直线AP与平面AA′B′B所成角为θ和异面直线AP与DC′所成角为α,
可得cos α=cos 〈,〉=,
sin θ=|cos 〈,〉|=,0
则||==
= ,
当x=时,线段DP长度的最小值为.
17.解析:(1)∵a∥b,∴==,解得x=2,y=-4,
故a=(2,4,1),b=(-2,-4,-1).
又因为b⊥c,所以b·c=0,即-6+8-z=0,解得z=2,
故c=(3,-2,2).
(2)由(1)可得a+c=(5,2,3),b+c=(1,-6,1),
设向量a+c与b+c所成的角为θ,|a+c|=,|b+c|=,
(a+c)·(b+c)=5-12+3=-4,
则cos θ==-.
18.解析:=+=+
=+(-)
=+[-(+)]
=-++.
所以=-a+b+c,
||2=2=
=(a2+b2+c2-2a·b-2a·c+2b·c)
=.
所以||=,即BN的长为.
19.解析:(1)证明:连接BD和A1B,由于=++,=-,=-,
∴·=·(-)=0,
∴⊥BD,
同理·=0,AC1⊥A1B,
且BD∩A1B=B,
所以AC1⊥平面A1BD.
(2)||2=(++)2=2+2+2+2·+2·+2·
=1+1+1+3×2×1×1×cos 60°=6.
∴||=.
∴||=||=.
20.解析:(1)证明:取PD的中点N,连接MN和AN,则MN∥DC且MN=DC,
又底面ABCD为正方形,∴MN∥AE且MN=AE=AB,
∴四边形MNAE为平行四边形,∴AN∥ME,
又AN 平面PAD,ME 平面PAD,
∴ME∥平面PAD.
(2)建立以D为坐标原点,,,分别为x轴,y轴,z轴正方向的空间直角坐标系,如图所示.
则P(0,0,1),A(1,0,0),C(0,1,0),E(1,,0),F(,1,0),所以=(-,,0),=(1,,-1),=(1,,0),设平面PEF的法向量为n=(x,y,z),则,即,
令x=2,则y=2,z=3,所以n=(2,2,3),
因为E,F分别为AB,BC的中点,所以EF∥AC.
又AC 平面PEF,EF 平面PEF,所以AC∥平面PEF;
因为=(0,,0),所以点A到平面PEF的距离d===.
所以直线AC到平面PEF的距离为.
21.解析:(1)证明:因为三棱柱ABC A1B1C1为正三棱柱,所以△ABC为正三角形,
因为Q为BC的中点,所以AQ⊥BC,
因为BB1⊥平面ABC,AQ 平面ABC,所以BB1⊥AQ,
因为BB1∩BC=B,BB1 平面BCC1B1,BC 平面BCC1B1,
所以AQ⊥平面BCC1B1,
又因为AQ 平面AQC1,所以平面AQC1⊥平面BCC1B1.
(2)设AC,A1C1的中点分别为O,O1,由三棱柱ABC A1B1C1为正三棱柱可知,
OB⊥OC,OB⊥OO1,OO1⊥OC,以{OB,OC,OO1}为基底建立空间直角坐标系O xyz.
因为AB=AA1=2,所以A(0,-1,0),B(,0,0),C(0,1,0),B1(,0,2),C1(0,1,2),
因为Q为BC的中点,所以Q(,,0),
所以=(,,0),=(0,2,2),=(0,0,2),
设n=(x,y,z)为平面AQC1的法向量,
所以直线CC1与平面AQC1所成角的正弦值为.
22.解析:(1)证明:连接CE,∵E为AD的中点,AD=2AB=2,∴AE=AB=,
∵ABCD为长方形,∴AB⊥AD,AD=BC=2,
在△ABE中,BE===2,
同理EC=2,∴BE2+EC2=BC2,∴CE⊥BE,
在折叠后的图形中:
∵平面ABE⊥平面BCDE,平面ABE∩平面BCDE=BE,CE⊥BE,∴CE⊥平面ABE,
又AB 平面ABE,∴CE⊥AB,
又∵AE⊥AB,CE 平面AEC,AE 平面AEC,CE∩AE=E,∴AB⊥平面AEC,
又AC 平面AEC,∴AB⊥AC.
(2)由(1)可知:△ABE,△BEC均为等腰直角三角形,过A点作底边BE的高,交BE于O点,以O为原点建立空间直角坐标系,如图所示:
则A(0,0,1),B(1,0,0),C(-1,2,0),E(-1,0,0),=(1,0,1),=(-1,2,-1),=(2,0,0),
易知平面ABE的一个法向量为m=(0,1,0),
假设在线段AC上存在点F,使二面角A BE F的余弦值为,
设=λ,则=+λ=(1-λ,2λ,1-λ),
设平面BEF的一个法向量为n=(x,y,z),∴,∴,
取y=1,则n=(0,1,),
cos 〈m,n〉==,∴λ=,
即当点F为线段AC靠近A的四等分点时,二面角A BE F的余弦值为.
