华师大版数学七年级下册 10.1.1生活中的轴对称课件(共14张PPT)
文档属性
| 名称 | 华师大版数学七年级下册 10.1.1生活中的轴对称课件(共14张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-12 22:44:13 | ||
图片预览





文档简介
(共14张PPT)
第10章 轴对称、平移与旋转
10.1 轴对称
1. 生活中的轴对称
一
学习目标
1. 通过实例欣赏,了解轴对称、对称轴以及轴对称图形的概念.
2. 在主体探究活动中,培养学生动手操作、观察、概括的能力.
3. 通过关注生活中的对称,体会“对称美”,激发学生学习数学的兴趣.
二
重难点
重点:通过实际操作理解轴对称图形的特点、轴对称的含义、性质、判定.难点:通过实例欣赏得出轴对称图形、对称轴的含义.
1.情景导入
三
教学过程
这些图形形状有什么共同特点?
2.探究新知
我们一起来欣赏这几幅图.
这几幅图相信你们都可能见过,把它们沿某条直线对折,对折后的两部分能完全重合,即为轴对称图形,这条直线即为这个图形的对称轴.
能不能自己动手创作一些对称图形呢?
试一试:在纸上滴几滴墨水,把纸张对折,随后打开,看看形成的两块墨迹是不是关于折痕对称.画出它的对称轴.
两个图形中的对应点(即两个图形重合时互相重合的点)叫做对称点.
不难发现,轴对称图形(或成对称轴的两个图形)沿对称轴对折后的两部分是完全重合的,所以轴对称图形(或成对称轴的两个图形)的对应线段(对折后重合的线段)相等,对应角(对折后重合的角)相等.
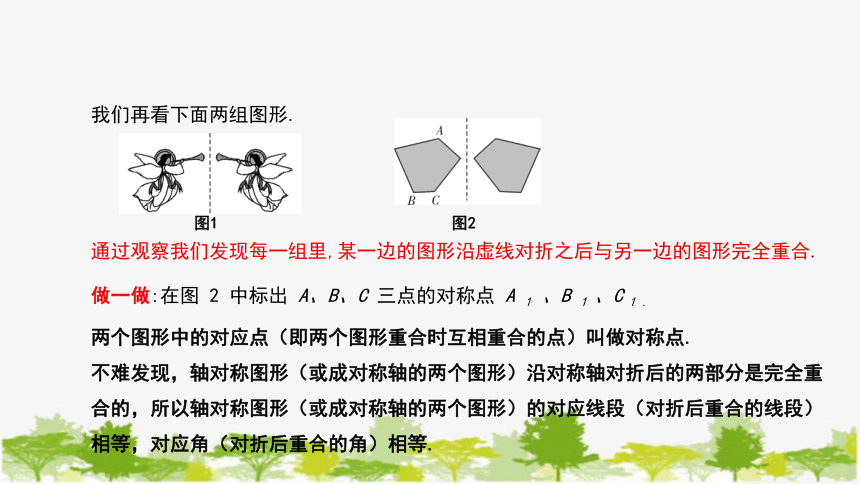
我们再看下面两组图形.
通过观察我们发现每一组里,某一边的图形沿虚线对折之后与另一边的图形完全重合.
图2
图1
做一做:在图 2 中标出 A、B、C 三点的对称点 A 1 、B 1 、C 1 .
【知识归纳】
(1)把一个图形沿着某一条直线翻折过去,如果它能够与另一个图形重合,那么就说这两个图形成轴对称,这条直线就是对称轴,两个图形中的对应点(即两个图形重合时互相重合的点)叫做对称点.
(2)轴对称图形(或成对称轴的两个图形)的对应线段(对折后重合的线段)相等,对应角(对折后重合的角)相等,这是轴对称图形的基本特征.
【知识归纳】
(3)轴对称图形及两个图形成轴对称区别与联系
区别:轴对称图形表述的是一个具有特殊形状的图形;两个图形成轴对称表述 的是两个图形的位置关系.
联系:都是沿一条直线折叠后能够互相重合.
转化:如果把轴对称图形沿对称轴分成两部分,那么这两个图形就关于这条直线对称;如果把两个成轴对称图形看成一个整体,那么它就是一个轴对称图形.
加拿大
摩洛哥
古巴
瑞典
以色列
巴西
3.例题精讲
例1 国旗是国家的一个象征,观察下面的国旗,哪些是轴对称图形?试找出它们的对称轴.
解:(1)(2)
(4)(5)
例2 请看,圆有几条对称轴
啊!无数条!
4.巩固练习 完成教材课后同步练习
5.课堂小结
(1)两图形成轴对称:把一个图形沿着某一条直线翻折过去,如果它能够与另一个图形重合,那么就说这两个图形成轴对称.
对称轴:是一条直线.
对称点:两个图形中的对应点(即两个图形重合时互相重合的点).
(2)轴对称图形的基本特征:轴对称图形(或成轴对称的两个图形)的对应线段(对折后重合的线段)相等,对应角(对折后重合的角)相等.
(3)轴对称图形及两个图形成轴对称区别与联系
区别:轴对称图形表述的是一个具有特殊形状的图形;两个图形成轴对称表述的是两个图形的位置关系.
联系:都是沿一条直线折叠后能够互相重合.
转化:如果把轴对称图形沿对称轴分成两部分,那么这两个图形就关于这条直线对称;如果把两个成轴对称图形看成一个整体,那么它就是一个轴对称图形.
第10章 轴对称、平移与旋转
10.1 轴对称
1. 生活中的轴对称
一
学习目标
1. 通过实例欣赏,了解轴对称、对称轴以及轴对称图形的概念.
2. 在主体探究活动中,培养学生动手操作、观察、概括的能力.
3. 通过关注生活中的对称,体会“对称美”,激发学生学习数学的兴趣.
二
重难点
重点:通过实际操作理解轴对称图形的特点、轴对称的含义、性质、判定.难点:通过实例欣赏得出轴对称图形、对称轴的含义.
1.情景导入
三
教学过程
这些图形形状有什么共同特点?
2.探究新知
我们一起来欣赏这几幅图.
这几幅图相信你们都可能见过,把它们沿某条直线对折,对折后的两部分能完全重合,即为轴对称图形,这条直线即为这个图形的对称轴.
能不能自己动手创作一些对称图形呢?
试一试:在纸上滴几滴墨水,把纸张对折,随后打开,看看形成的两块墨迹是不是关于折痕对称.画出它的对称轴.
两个图形中的对应点(即两个图形重合时互相重合的点)叫做对称点.
不难发现,轴对称图形(或成对称轴的两个图形)沿对称轴对折后的两部分是完全重合的,所以轴对称图形(或成对称轴的两个图形)的对应线段(对折后重合的线段)相等,对应角(对折后重合的角)相等.
我们再看下面两组图形.
通过观察我们发现每一组里,某一边的图形沿虚线对折之后与另一边的图形完全重合.
图2
图1
做一做:在图 2 中标出 A、B、C 三点的对称点 A 1 、B 1 、C 1 .
【知识归纳】
(1)把一个图形沿着某一条直线翻折过去,如果它能够与另一个图形重合,那么就说这两个图形成轴对称,这条直线就是对称轴,两个图形中的对应点(即两个图形重合时互相重合的点)叫做对称点.
(2)轴对称图形(或成对称轴的两个图形)的对应线段(对折后重合的线段)相等,对应角(对折后重合的角)相等,这是轴对称图形的基本特征.
【知识归纳】
(3)轴对称图形及两个图形成轴对称区别与联系
区别:轴对称图形表述的是一个具有特殊形状的图形;两个图形成轴对称表述 的是两个图形的位置关系.
联系:都是沿一条直线折叠后能够互相重合.
转化:如果把轴对称图形沿对称轴分成两部分,那么这两个图形就关于这条直线对称;如果把两个成轴对称图形看成一个整体,那么它就是一个轴对称图形.
加拿大
摩洛哥
古巴
瑞典
以色列
巴西
3.例题精讲
例1 国旗是国家的一个象征,观察下面的国旗,哪些是轴对称图形?试找出它们的对称轴.
解:(1)(2)
(4)(5)
例2 请看,圆有几条对称轴
啊!无数条!
4.巩固练习 完成教材课后同步练习
5.课堂小结
(1)两图形成轴对称:把一个图形沿着某一条直线翻折过去,如果它能够与另一个图形重合,那么就说这两个图形成轴对称.
对称轴:是一条直线.
对称点:两个图形中的对应点(即两个图形重合时互相重合的点).
(2)轴对称图形的基本特征:轴对称图形(或成轴对称的两个图形)的对应线段(对折后重合的线段)相等,对应角(对折后重合的角)相等.
(3)轴对称图形及两个图形成轴对称区别与联系
区别:轴对称图形表述的是一个具有特殊形状的图形;两个图形成轴对称表述的是两个图形的位置关系.
联系:都是沿一条直线折叠后能够互相重合.
转化:如果把轴对称图形沿对称轴分成两部分,那么这两个图形就关于这条直线对称;如果把两个成轴对称图形看成一个整体,那么它就是一个轴对称图形.
