2023年山东省济南市中考数学模拟预测定心卷(三)(无答案)
文档属性
| 名称 | 2023年山东省济南市中考数学模拟预测定心卷(三)(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 561.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-13 09:05:41 | ||
图片预览


文档简介
2023年济南市中考数学模拟预测定心卷(三)
总分:150分 时间:120分钟
选择题部分 共40分
一、选择题(本大题共10个小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.的算术平方根是( )
A.4 B.±4 C.2 D.±2
2.下面四个几何体中,主视图为三角形的是( )
3.人体中红细胞的直径约为0.000 007 7 m,0.000 007 7用科学记数法表示是( )
A.0.77×10-5 B.0.77×10-6 C.7.7×10-5 D.7.7×10-6
4.如图,直线AD∥BC,若∠1=42°,∠BAC=78°,则∠2的度数为( )
A.42° B.50° C.60° D.68°
5.下列运算正确的是( )
A.(a3)2=a6 B.2a+3a=5a2 C.a8÷a4=a2 D.a2·a3=a6
6.“国士无双”是人民对“杂交水稻之父”袁隆平院士的赞誉.下列四个汉字中是轴对称图形的是( )
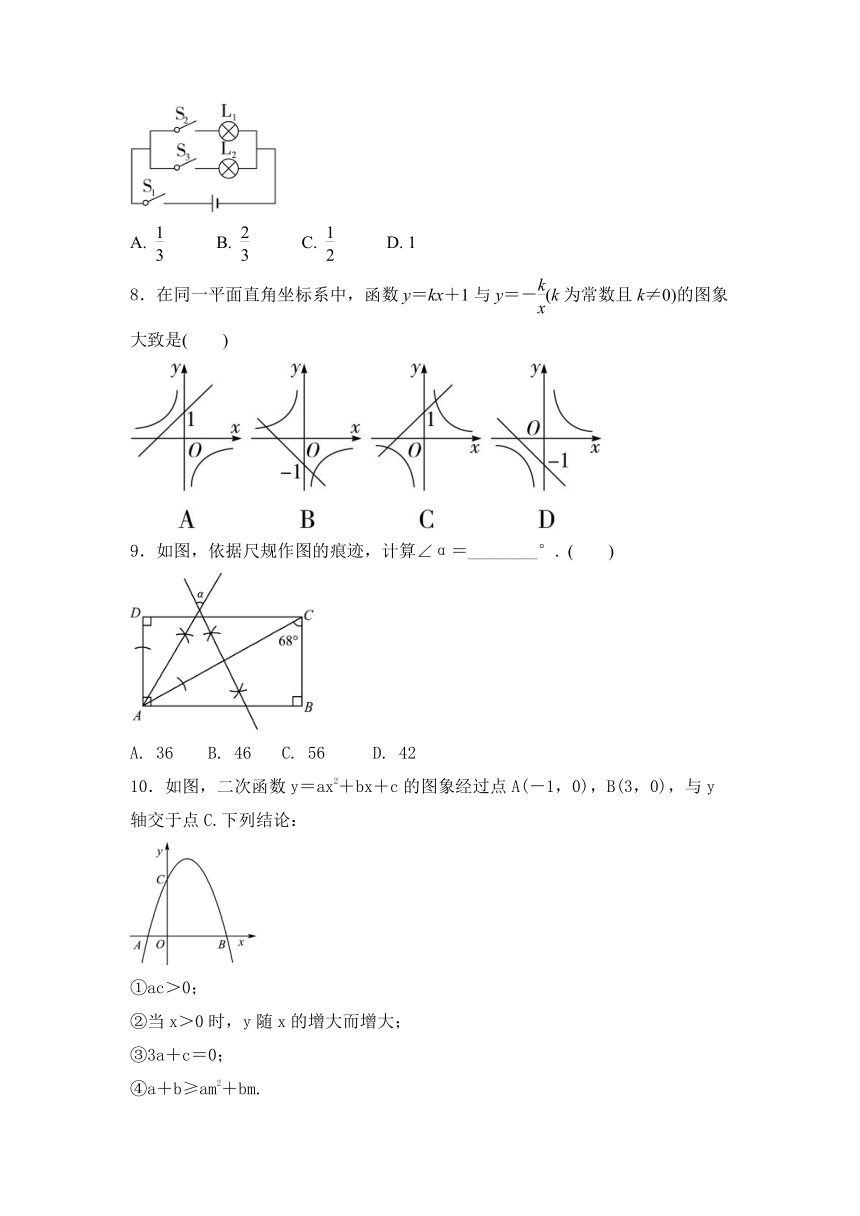
7.如图所示的电路图,同时闭合两个开关能形成闭合电路的概率是( )
A. B. C. D. 1
8.在同一平面直角坐标系中,函数y=kx+1与y=-(k为常数且k≠0)的图象大致是( )
9.如图,依据尺规作图的痕迹,计算∠α=________°. ( )
A. 36 B. 46 C. 56 D. 42
10.如图,二次函数y=ax2+bx+c的图象经过点A(-1,0),B(3,0),与y轴交于点C.下列结论:
①ac>0;
②当x>0时,y随x的增大而增大;
③3a+c=0;
④a+b≥am2+bm.
其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
非选择题部分 共110分
二、填空题:(本大题共6个小题,每小题4分,共24分.)
11.分解因式:2x3-18xy2=________.
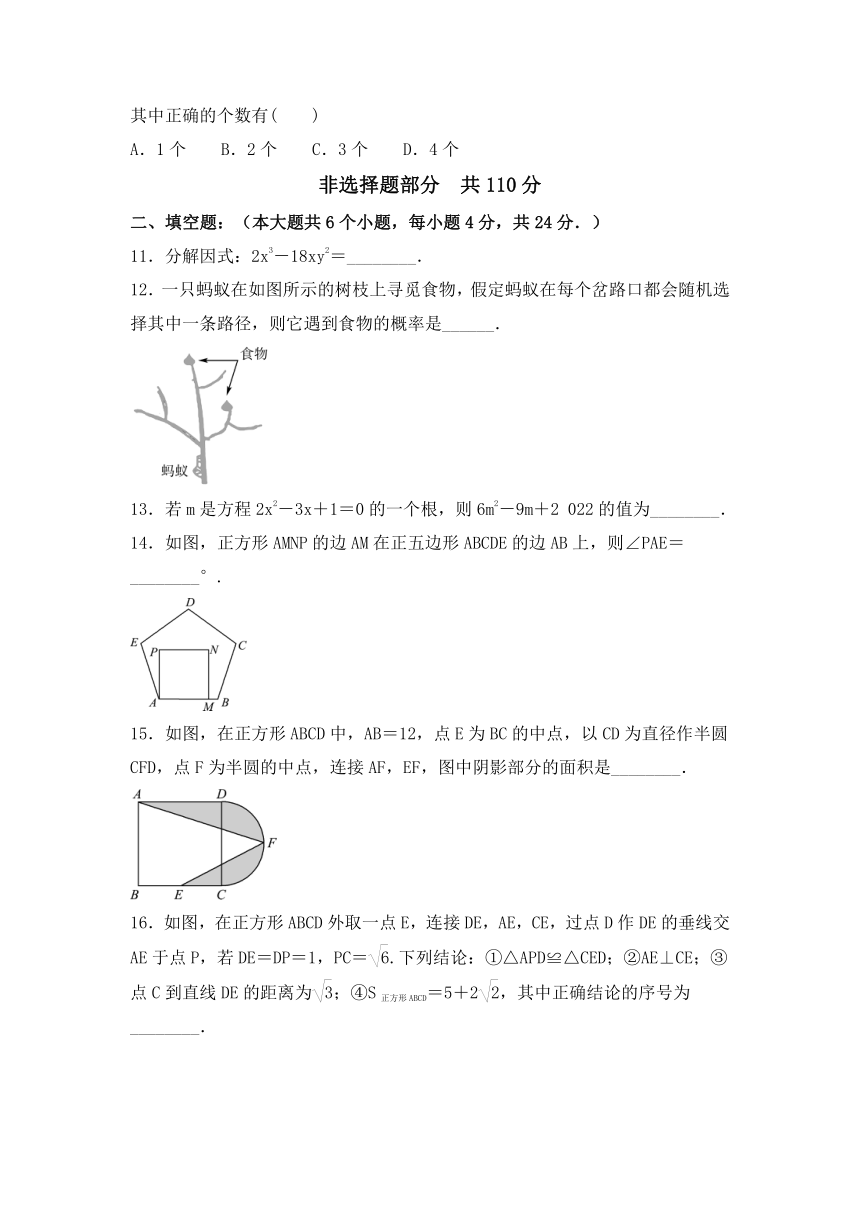
12.一只蚂蚁在如图所示的树枝上寻觅食物,假定蚂蚁在每个岔路口都会随机选择其中一条路径,则它遇到食物的概率是______.
13.若m是方程2x2-3x+1=0的一个根,则6m2-9m+2 022的值为________.
14.如图,正方形AMNP的边AM在正五边形ABCDE的边AB上,则∠PAE=________°.
15.如图,在正方形ABCD中,AB=12,点E为BC的中点,以CD为直径作半圆CFD,点F为半圆的中点,连接AF,EF,图中阴影部分的面积是________.
16.如图,在正方形ABCD外取一点E,连接DE,AE,CE,过点D作DE的垂线交AE于点P,若DE=DP=1,PC=.下列结论:①△APD≌△CED;②AE⊥CE;③点C到直线DE的距离为;④S正方形ABCD=5+2,其中正确结论的序号为________.
三、解答题:(本大题共10个小题,共86分.解答应写出文字说明、证明过程或演算步骤.)
17.计算:计算:+(π-2023)0-()-1-|1-|.
18.解不等式组并写出它的整数解.
19.如图,在菱形ABCD中,点M,N分别在AB,CB上,且∠ADM=∠CDN.
求证:BM=BN.
20. 为了了解某校九年级全体男生1 000米跑步的成绩,随机抽取了部分男生进行测试.并将测试成绩分为A,B,C,D四个成绩,绘制了如下不完整的统计图表.
成绩等级频数分布表
根据图表信息解答下列问题:
(1)填空:x=________,y=________,扇形统计图中表示A的扇形的圆心角度数为________;
(2)甲、乙、丙是A等级中的3名学生.学校决定从这3名学生中随机抽取2名来介绍体育锻炼经验,求同时抽到甲、乙2名学生的概率.
21. 随着科技的发展,无人机已广泛应用于生产和生活,如代替人们在高空测量距离和角度.某校“综合与实践”活动小组的同学要测量AB,CD两座楼之间的距离,他们借助无人机设计了如下测量方案:无人机在AB,CD两楼之间上方的点O处,点O距地面AC的高度为60 m,此时观测到楼AB底部点A处的俯角为70°,楼CD上点E处的俯角为30°,沿水平方向由点O飞行24 m到达点F,测得点E处俯角为60°,其中点A,B,C,D,E,F,O均在同一竖直平面内.请根据以上数据求楼AB与CD之间的距离AC的长(结果精确到1 m.参考数据:sin 70°≈0.94,cos 70°≈0.34,tan 70°≈2.75,≈1.73).
22. 如图,AB是⊙O的直径,点C是⊙O上一点,∠CAB的平分线AD交于点D,过点D作DE∥BC交AC的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)过点D作DF⊥AB于点F,连接BD.若OF=1,BF=2,求BD的长度.
23.某商店准备购进A,B两种商品,A种商品每件的进价比B种商品每件的进价多20元,用2 000元购进A种商品和用1 200元购进B种商品的数量相同.商店将A种商品每件的售价定为80元,B种商品每件的售价定为45元.
(1)A种商品每件的进价和B种商品每件的进价分别是多少元;
(2)商店计划用不超过1 560元的资金购进A,B两种商品共40件,其中A种商品的数量不低于B种商品数量的一半,该商店有几种进货方案.
24.如图,一次函数y=-x+1的图象与x轴、y轴分别交于点A,B,以线段AB为边在第一象限作等边△ABC.
(1)若点C在反比例函数y=的图象上,求该反比例函数的解析式;
(2)点P(2,m)在第一象限,过点P作x轴的垂线,垂足为D,当△PAD与△OAB相似时,点P是否在(1)中反比例函数图象上?如果在,求出P点坐标;如果不在,请加以说明.
25.【发现】 如图1,已知等边三角形ABC,将直角三角板的60°角顶点D任意放在BC边上(点D不与点B,C重合),使两边分别交线段AB,AC于点E,F.
(1)若AB=6,AE=4,BD=2,则CF=________;
(2)求证:△EBD∽△DCF;
【思考】 若将图1中的三角板的顶点D在BC边上移动,保持三角板与边AB,AC的两个交点E,F都存在,连接EF,如图2所示,问:点D是否存在某一位置,使ED平分∠BEF且FD平分∠CFE?若存在,求出的值;若不存在,请说明理由;
【探索】 如图3,在等腰三角形ABC中,AB=AC,点O为BC边的中点,将三角形透明纸板的一个顶点放在点O处(其中∠MON=∠B),使两条边分别交边AB,AC于点E,F(点E,F均不与△ABC的顶点重合),连接EF.设∠B=α,则△AEF与△ABC的周长之比为________.(用含α的解析式表示)
图1 图2 图3
26.如图,在平面直角坐标系xOy中,抛物线y=-x2+x+4与两坐标轴分别相交于A,B,C三点.
(1)求证:∠ACB=90°;
(2)点D是第一象限内该抛物线上的动点,过点D作x轴的垂线交BC于点E,交x轴于点F.
①求DE+BF的最大值;
②点G是AC的中点,若以点C,D,E为顶点的三角形与△AOG相似,求点D的坐标.
总分:150分 时间:120分钟
选择题部分 共40分
一、选择题(本大题共10个小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.的算术平方根是( )
A.4 B.±4 C.2 D.±2
2.下面四个几何体中,主视图为三角形的是( )
3.人体中红细胞的直径约为0.000 007 7 m,0.000 007 7用科学记数法表示是( )
A.0.77×10-5 B.0.77×10-6 C.7.7×10-5 D.7.7×10-6
4.如图,直线AD∥BC,若∠1=42°,∠BAC=78°,则∠2的度数为( )
A.42° B.50° C.60° D.68°
5.下列运算正确的是( )
A.(a3)2=a6 B.2a+3a=5a2 C.a8÷a4=a2 D.a2·a3=a6
6.“国士无双”是人民对“杂交水稻之父”袁隆平院士的赞誉.下列四个汉字中是轴对称图形的是( )
7.如图所示的电路图,同时闭合两个开关能形成闭合电路的概率是( )
A. B. C. D. 1
8.在同一平面直角坐标系中,函数y=kx+1与y=-(k为常数且k≠0)的图象大致是( )
9.如图,依据尺规作图的痕迹,计算∠α=________°. ( )
A. 36 B. 46 C. 56 D. 42
10.如图,二次函数y=ax2+bx+c的图象经过点A(-1,0),B(3,0),与y轴交于点C.下列结论:
①ac>0;
②当x>0时,y随x的增大而增大;
③3a+c=0;
④a+b≥am2+bm.
其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
非选择题部分 共110分
二、填空题:(本大题共6个小题,每小题4分,共24分.)
11.分解因式:2x3-18xy2=________.
12.一只蚂蚁在如图所示的树枝上寻觅食物,假定蚂蚁在每个岔路口都会随机选择其中一条路径,则它遇到食物的概率是______.
13.若m是方程2x2-3x+1=0的一个根,则6m2-9m+2 022的值为________.
14.如图,正方形AMNP的边AM在正五边形ABCDE的边AB上,则∠PAE=________°.
15.如图,在正方形ABCD中,AB=12,点E为BC的中点,以CD为直径作半圆CFD,点F为半圆的中点,连接AF,EF,图中阴影部分的面积是________.
16.如图,在正方形ABCD外取一点E,连接DE,AE,CE,过点D作DE的垂线交AE于点P,若DE=DP=1,PC=.下列结论:①△APD≌△CED;②AE⊥CE;③点C到直线DE的距离为;④S正方形ABCD=5+2,其中正确结论的序号为________.
三、解答题:(本大题共10个小题,共86分.解答应写出文字说明、证明过程或演算步骤.)
17.计算:计算:+(π-2023)0-()-1-|1-|.
18.解不等式组并写出它的整数解.
19.如图,在菱形ABCD中,点M,N分别在AB,CB上,且∠ADM=∠CDN.
求证:BM=BN.
20. 为了了解某校九年级全体男生1 000米跑步的成绩,随机抽取了部分男生进行测试.并将测试成绩分为A,B,C,D四个成绩,绘制了如下不完整的统计图表.
成绩等级频数分布表
根据图表信息解答下列问题:
(1)填空:x=________,y=________,扇形统计图中表示A的扇形的圆心角度数为________;
(2)甲、乙、丙是A等级中的3名学生.学校决定从这3名学生中随机抽取2名来介绍体育锻炼经验,求同时抽到甲、乙2名学生的概率.
21. 随着科技的发展,无人机已广泛应用于生产和生活,如代替人们在高空测量距离和角度.某校“综合与实践”活动小组的同学要测量AB,CD两座楼之间的距离,他们借助无人机设计了如下测量方案:无人机在AB,CD两楼之间上方的点O处,点O距地面AC的高度为60 m,此时观测到楼AB底部点A处的俯角为70°,楼CD上点E处的俯角为30°,沿水平方向由点O飞行24 m到达点F,测得点E处俯角为60°,其中点A,B,C,D,E,F,O均在同一竖直平面内.请根据以上数据求楼AB与CD之间的距离AC的长(结果精确到1 m.参考数据:sin 70°≈0.94,cos 70°≈0.34,tan 70°≈2.75,≈1.73).
22. 如图,AB是⊙O的直径,点C是⊙O上一点,∠CAB的平分线AD交于点D,过点D作DE∥BC交AC的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)过点D作DF⊥AB于点F,连接BD.若OF=1,BF=2,求BD的长度.
23.某商店准备购进A,B两种商品,A种商品每件的进价比B种商品每件的进价多20元,用2 000元购进A种商品和用1 200元购进B种商品的数量相同.商店将A种商品每件的售价定为80元,B种商品每件的售价定为45元.
(1)A种商品每件的进价和B种商品每件的进价分别是多少元;
(2)商店计划用不超过1 560元的资金购进A,B两种商品共40件,其中A种商品的数量不低于B种商品数量的一半,该商店有几种进货方案.
24.如图,一次函数y=-x+1的图象与x轴、y轴分别交于点A,B,以线段AB为边在第一象限作等边△ABC.
(1)若点C在反比例函数y=的图象上,求该反比例函数的解析式;
(2)点P(2,m)在第一象限,过点P作x轴的垂线,垂足为D,当△PAD与△OAB相似时,点P是否在(1)中反比例函数图象上?如果在,求出P点坐标;如果不在,请加以说明.
25.【发现】 如图1,已知等边三角形ABC,将直角三角板的60°角顶点D任意放在BC边上(点D不与点B,C重合),使两边分别交线段AB,AC于点E,F.
(1)若AB=6,AE=4,BD=2,则CF=________;
(2)求证:△EBD∽△DCF;
【思考】 若将图1中的三角板的顶点D在BC边上移动,保持三角板与边AB,AC的两个交点E,F都存在,连接EF,如图2所示,问:点D是否存在某一位置,使ED平分∠BEF且FD平分∠CFE?若存在,求出的值;若不存在,请说明理由;
【探索】 如图3,在等腰三角形ABC中,AB=AC,点O为BC边的中点,将三角形透明纸板的一个顶点放在点O处(其中∠MON=∠B),使两条边分别交边AB,AC于点E,F(点E,F均不与△ABC的顶点重合),连接EF.设∠B=α,则△AEF与△ABC的周长之比为________.(用含α的解析式表示)
图1 图2 图3
26.如图,在平面直角坐标系xOy中,抛物线y=-x2+x+4与两坐标轴分别相交于A,B,C三点.
(1)求证:∠ACB=90°;
(2)点D是第一象限内该抛物线上的动点,过点D作x轴的垂线交BC于点E,交x轴于点F.
①求DE+BF的最大值;
②点G是AC的中点,若以点C,D,E为顶点的三角形与△AOG相似,求点D的坐标.
同课章节目录
