河南省南阳市名校2022-2023学年高一下学期6月第四次月考数学试题(含答案)
文档属性
| 名称 | 河南省南阳市名校2022-2023学年高一下学期6月第四次月考数学试题(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 101.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-11 00:00:00 | ||
图片预览




文档简介
南阳市名校2022-2023学年高一下学期6月第四次月考
数学试题
一、单选题(本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,有且只有一项是符合要求的)
1. 若tanα>0,,则角α的终边在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2. 如图所示,水平放置的一个平面图形的直观图是边长为的正方形,则原图形的周长是( )
A. 8cm B. 10cm C. 6cm D. 12cm
3. 若z=1+i,则( )
A. 0 B. 1 C. D. 2
4. 设a,b,c表示不同直线,,表示不同平面,下列命题:①若,,则;②若,,则③若,,则: ④若,,,则其中真命题的个数是( )
A. 1 B. 2 C. 3 D. 4
5. 已知,则( )
A. B. C. D.
6. 已知函数,则下面结论错误的是( )
A. 当时,f(x)的取值范围是
B. y=f(x)在上单调递减
C. y=f(x)的图像关于直线对称
D. y=f(x)的图像可由函数的图像向右平移个单位得到
7. 已知圆锥的母线长为2,底面半径为,则过顶点的截面面积的最大值等于( )
A. B. C. 3 D. 2
8. 设,,,则有( )
A. a>b>c B. a二、多选题(本题共4小题,每小题5分,共20分,在每小题给出的选项中,有多项符合题目要求,全部选对得5分,部分选对的得2分,有选错的得0分)
9. 下列说法不正确的是( )
A. 底面是矩形的四棱柱是长方体
B. 有两个面平行,其余四个面都是平行四边形的几何体叫平行六面体
C. 棱柱的各个侧面都是平行四边形
D. 有两个面平行,其余各面都是四边形的几何体叫棱柱
10. 已知复数,,则( )
A.
B. 复数的虚部为
C. 复数与在复平面内所对应的点位于同一象限
D. 复数在复平面内对应的点在函数的图像上
11. 已知向量,,则下列说法正确的是( )
A. 若,则
B. 若,则
C. 的最大值为2
D. 的取值范围是[1,3]
12. 已知为的重心,D为边的中点,则( )
A.
B.
C.
D.
三、填空题(本题共4小题,每小题5分,共20分)
13. 若满足,AC=6,BC=k的恰有一个,则的取值范围是______.
14. 在正方体中,E是的中点,连接DE、,则异面直线DE、所成角的正弦值为____.
15. 已知向量,且,则______.
16. 已知中,点在边上,,AD=2,CD=2BD.当取得最小值时,BD=_____.
四、解答题(本题共6小题,共70分)
17. (10分)已知复数,其中且a>0,i为虚数单位,且为纯虚数
(1)求实数的值;
(2)若,求复数并指出其对应复平面内的点所在的象限.
18. (12分)已知向量,满足,,与不共线.
(1)若向量与为方向相反的向量,求实数的值;
(2)若向量与的夹角为,求与的夹角
19. (12分)已知a,为锐角,,
(1)求cos2α的值; (2)求的值.
20. (12分)如图,已知点是正方形所在平面外一 点,M,N分别是AB,PC的中点.
(1)求证:MN∥平面PAD;
(2)若中点为Q,求证:平面平面PAD.
(3)若平面ABCD,AB=PA=2,求直线与面 PAD所成的角.
21. (12分)在锐角中,角A,B,C的对边分别为a,b,c,且.
(I)求角的大小; (Ⅱ)求的取值范围
22. (12分)已知函数的最小正周期为,且直线是其图象的一条对称轴
(1)求函数的解析式;
(2)将函数的图象向右平移个单位,再将所得的图象上每一点的纵坐标不变,横坐标伸长为原来的倍后所得到的图象对应的函数记作y=g(x),已知常数,且函数在(0,nπ)内恰有个零点,求常数与n的值.
南阳市名校2022-2023学年高一下学期6月第四次月考
数学答案
一、单选题
1.C 2.A 3.D 4.A 5.A 6.D 7.D 8.C
二、多选题
9.ABD 10.BC 11.ACD 12.ABC
三、填空题
13.
14.
15.
16. 【详解】[方法一]:余弦定理
设CD=2BD=2m>0,
则在中,,
在中,ADcOs∠ADC=4m2+4-4m,
所以
当且仅当即时,等号成立
所以当取最小值时,
故答案为:.
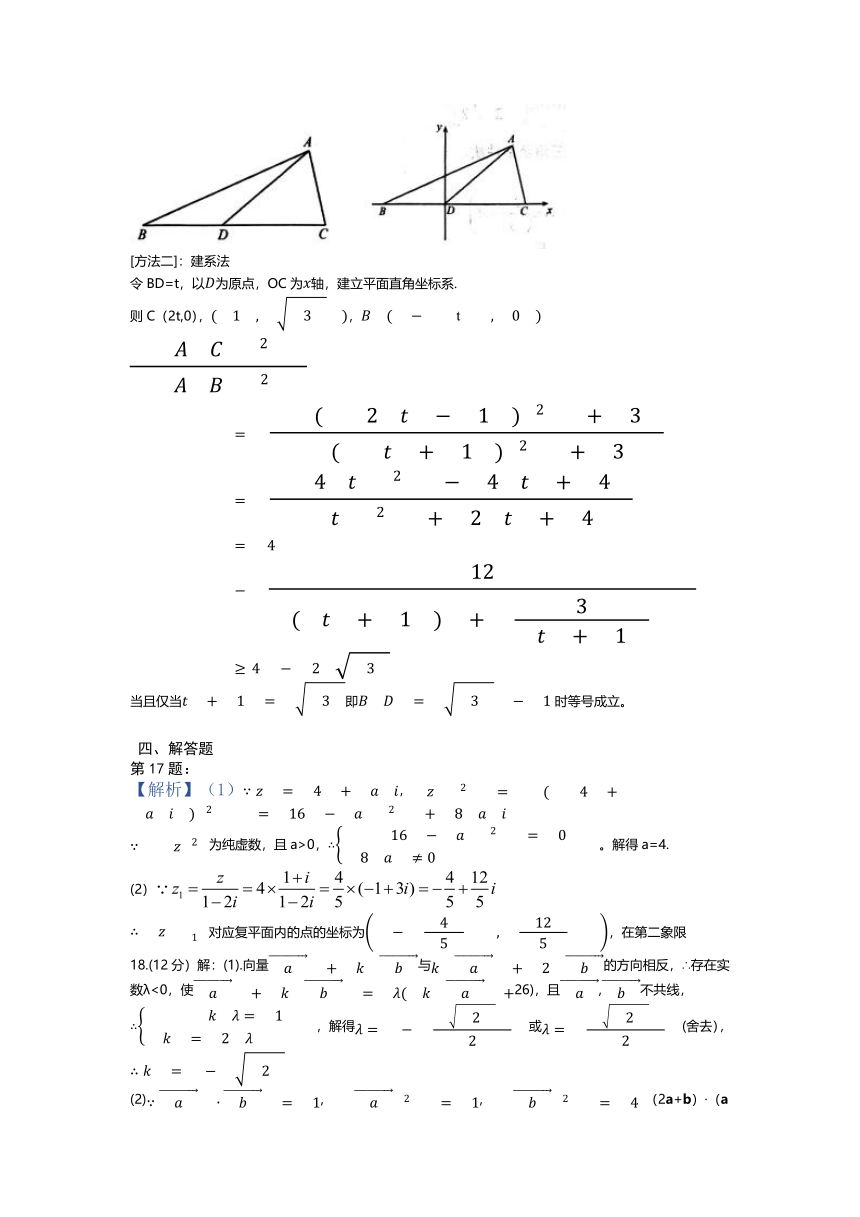
[方法二]:建系法
令BD=t,以为原点,OC为轴,建立平面直角坐标系.
则C(2t,0),,
当且仅当即时等号成立。
四、解答题
第17题:
【解析】(1),
为纯虚数,且a>0,∴。解得a=4.
(2)
对应复平面内的点的坐标为,在第二象限
18.(12分)解:(1).向量与的方向相反,∴存在实数λ<0,使26),且,不共线,∴,解得或(舍去),
(2),, (2a+b)·(a-b)=-3
且
∴
19.(12分)解:(1)因为,,所以因为,所以, 因此,
(2)因为α,为锐角,所以又因为,所以因此. 因为,所以, 因此.
20.(1)证明见解析证明见解析(3)
【详解】(1)取的中点E,连接AE,NE, 因为是PC的中点,所以且, 又是AB的中点,ABCD是正方形,所以AM∥DC且, 所以且NE=AM, 所以四边形为平行四边形,所以, 又平面PAD,AE平面PAD, 所以MN∥平面PAD.
(2)因为为PB的中点,M是的中点 ,所以MQ∥AP,又MQ平面PAD,平面PAD, 所以MQ∥平面PAD, 又MN∥平面PAD,MQ MN=M, MQ,MNc平面MNQ,所以平面平面PAD.
(3)因为平面ABCD,平面PAD, 所以平面平面ABCD, 又为正方形,所以,AB平面ABCD,平面 平面ABCD=AD, 所以平面PAD, 所以即为直线与面所成的角,又AB=PA=2,所以为等腰直角三角 形,所以,即直线与面所成的角为.
21.(12分)(1)
【详解】(1)[方法一]:余弦定理 由,得,即结合余弦定,即即即2, 即∵为锐角三角形,,, 所以又为的一个内角,故
[方法二]【最优解】:正弦定理边化角 由2bsin,结合正弦定理可得:2sinBsin4=<5 sinA4,∴为锐角三角形,故. (Ⅱ)[方法一]:余弦定理基本不等式 因为,并利用余弦定理整理得即. 结合,得由临界状态(不妨取可知而为锐角三角形,所以由余弦定理得,代入化简得故cos A+cosB+cosC的取值范围是
22.(12分)(1);(2)λ=-1,n=1347.
【详解】(1)由三角函数的周期公式可得,令,得由于直线为函数的一条对称轴,所以,, 得,由于,∴k=-1,则, 因此,:
(2)将函数的图象向右平移个单位, 得到函数, 再将所得的图象上每一点的纵坐标不变,横坐标伸长为原来的倍后所得到的图象对应的函数为g(x)=sinx, 令,可得, 令,得,, 则关于的二次方程必有两不等实根、,则,则、异号,
(i)当且时,则方程和在区间均有偶数个根, 从而方程在也有偶数个根,不合乎题意;
(ii)当,则,当时,只有一根,有两根. 所以,关于的方程在上有三个根
由于2021=3×673+2,则方程在(0,1346π)上有3×673=2019个根, 由于方程在区间(1346π,1367π)上只有一个根,在区间(1367π,1368π)上无实解,方程在区间上无实数解,在区间(1367π,1368π)上有两个根,因此,关于的方程在区间(0,1347π)上有个根,在区间上有个根, 不合乎题意;
(iii)当时,则,当时,只有一根,有两根
所以,关于的方程在上有三个根,
由于2021=3×673+2,则方程在(0,1346π)上有3×673=2019个根
由于方程在区间上无实数根,在区间(1347π,1348π)上只有一个实数根, 方程在区间上有两个实数解,在区间上无实数解,
因此,关于的方程在区间(0,1347π)上有个根,在区间 (0,1348π)上有个根,此时,,得=-1.
综上所述:=-1,n=1347.
数学试题
一、单选题(本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,有且只有一项是符合要求的)
1. 若tanα>0,,则角α的终边在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2. 如图所示,水平放置的一个平面图形的直观图是边长为的正方形,则原图形的周长是( )
A. 8cm B. 10cm C. 6cm D. 12cm
3. 若z=1+i,则( )
A. 0 B. 1 C. D. 2
4. 设a,b,c表示不同直线,,表示不同平面,下列命题:①若,,则;②若,,则③若,,则: ④若,,,则其中真命题的个数是( )
A. 1 B. 2 C. 3 D. 4
5. 已知,则( )
A. B. C. D.
6. 已知函数,则下面结论错误的是( )
A. 当时,f(x)的取值范围是
B. y=f(x)在上单调递减
C. y=f(x)的图像关于直线对称
D. y=f(x)的图像可由函数的图像向右平移个单位得到
7. 已知圆锥的母线长为2,底面半径为,则过顶点的截面面积的最大值等于( )
A. B. C. 3 D. 2
8. 设,,,则有( )
A. a>b>c B. a
9. 下列说法不正确的是( )
A. 底面是矩形的四棱柱是长方体
B. 有两个面平行,其余四个面都是平行四边形的几何体叫平行六面体
C. 棱柱的各个侧面都是平行四边形
D. 有两个面平行,其余各面都是四边形的几何体叫棱柱
10. 已知复数,,则( )
A.
B. 复数的虚部为
C. 复数与在复平面内所对应的点位于同一象限
D. 复数在复平面内对应的点在函数的图像上
11. 已知向量,,则下列说法正确的是( )
A. 若,则
B. 若,则
C. 的最大值为2
D. 的取值范围是[1,3]
12. 已知为的重心,D为边的中点,则( )
A.
B.
C.
D.
三、填空题(本题共4小题,每小题5分,共20分)
13. 若满足,AC=6,BC=k的恰有一个,则的取值范围是______.
14. 在正方体中,E是的中点,连接DE、,则异面直线DE、所成角的正弦值为____.
15. 已知向量,且,则______.
16. 已知中,点在边上,,AD=2,CD=2BD.当取得最小值时,BD=_____.
四、解答题(本题共6小题,共70分)
17. (10分)已知复数,其中且a>0,i为虚数单位,且为纯虚数
(1)求实数的值;
(2)若,求复数并指出其对应复平面内的点所在的象限.
18. (12分)已知向量,满足,,与不共线.
(1)若向量与为方向相反的向量,求实数的值;
(2)若向量与的夹角为,求与的夹角
19. (12分)已知a,为锐角,,
(1)求cos2α的值; (2)求的值.
20. (12分)如图,已知点是正方形所在平面外一 点,M,N分别是AB,PC的中点.
(1)求证:MN∥平面PAD;
(2)若中点为Q,求证:平面平面PAD.
(3)若平面ABCD,AB=PA=2,求直线与面 PAD所成的角.
21. (12分)在锐角中,角A,B,C的对边分别为a,b,c,且.
(I)求角的大小; (Ⅱ)求的取值范围
22. (12分)已知函数的最小正周期为,且直线是其图象的一条对称轴
(1)求函数的解析式;
(2)将函数的图象向右平移个单位,再将所得的图象上每一点的纵坐标不变,横坐标伸长为原来的倍后所得到的图象对应的函数记作y=g(x),已知常数,且函数在(0,nπ)内恰有个零点,求常数与n的值.
南阳市名校2022-2023学年高一下学期6月第四次月考
数学答案
一、单选题
1.C 2.A 3.D 4.A 5.A 6.D 7.D 8.C
二、多选题
9.ABD 10.BC 11.ACD 12.ABC
三、填空题
13.
14.
15.
16. 【详解】[方法一]:余弦定理
设CD=2BD=2m>0,
则在中,,
在中,ADcOs∠ADC=4m2+4-4m,
所以
当且仅当即时,等号成立
所以当取最小值时,
故答案为:.
[方法二]:建系法
令BD=t,以为原点,OC为轴,建立平面直角坐标系.
则C(2t,0),,
当且仅当即时等号成立。
四、解答题
第17题:
【解析】(1),
为纯虚数,且a>0,∴。解得a=4.
(2)
对应复平面内的点的坐标为,在第二象限
18.(12分)解:(1).向量与的方向相反,∴存在实数λ<0,使26),且,不共线,∴,解得或(舍去),
(2),, (2a+b)·(a-b)=-3
且
∴
19.(12分)解:(1)因为,,所以因为,所以, 因此,
(2)因为α,为锐角,所以又因为,所以因此. 因为,所以, 因此.
20.(1)证明见解析证明见解析(3)
【详解】(1)取的中点E,连接AE,NE, 因为是PC的中点,所以且, 又是AB的中点,ABCD是正方形,所以AM∥DC且, 所以且NE=AM, 所以四边形为平行四边形,所以, 又平面PAD,AE平面PAD, 所以MN∥平面PAD.
(2)因为为PB的中点,M是的中点 ,所以MQ∥AP,又MQ平面PAD,平面PAD, 所以MQ∥平面PAD, 又MN∥平面PAD,MQ MN=M, MQ,MNc平面MNQ,所以平面平面PAD.
(3)因为平面ABCD,平面PAD, 所以平面平面ABCD, 又为正方形,所以,AB平面ABCD,平面 平面ABCD=AD, 所以平面PAD, 所以即为直线与面所成的角,又AB=PA=2,所以为等腰直角三角 形,所以,即直线与面所成的角为.
21.(12分)(1)
【详解】(1)[方法一]:余弦定理 由,得,即结合余弦定,即即即2, 即∵为锐角三角形,,, 所以又为的一个内角,故
[方法二]【最优解】:正弦定理边化角 由2bsin,结合正弦定理可得:2sinBsin4=<5 sinA4,∴为锐角三角形,故. (Ⅱ)[方法一]:余弦定理基本不等式 因为,并利用余弦定理整理得即. 结合,得由临界状态(不妨取可知而为锐角三角形,所以由余弦定理得,代入化简得故cos A+cosB+cosC的取值范围是
22.(12分)(1);(2)λ=-1,n=1347.
【详解】(1)由三角函数的周期公式可得,令,得由于直线为函数的一条对称轴,所以,, 得,由于,∴k=-1,则, 因此,:
(2)将函数的图象向右平移个单位, 得到函数, 再将所得的图象上每一点的纵坐标不变,横坐标伸长为原来的倍后所得到的图象对应的函数为g(x)=sinx, 令,可得, 令,得,, 则关于的二次方程必有两不等实根、,则,则、异号,
(i)当且时,则方程和在区间均有偶数个根, 从而方程在也有偶数个根,不合乎题意;
(ii)当,则,当时,只有一根,有两根. 所以,关于的方程在上有三个根
由于2021=3×673+2,则方程在(0,1346π)上有3×673=2019个根, 由于方程在区间(1346π,1367π)上只有一个根,在区间(1367π,1368π)上无实解,方程在区间上无实数解,在区间(1367π,1368π)上有两个根,因此,关于的方程在区间(0,1347π)上有个根,在区间上有个根, 不合乎题意;
(iii)当时,则,当时,只有一根,有两根
所以,关于的方程在上有三个根,
由于2021=3×673+2,则方程在(0,1346π)上有3×673=2019个根
由于方程在区间上无实数根,在区间(1347π,1348π)上只有一个实数根, 方程在区间上有两个实数解,在区间上无实数解,
因此,关于的方程在区间(0,1347π)上有个根,在区间 (0,1348π)上有个根,此时,,得=-1.
综上所述:=-1,n=1347.
同课章节目录
