2022-2023学年高一下学期期末复习专题03 圆周运动的描述(含解析)
文档属性
| 名称 | 2022-2023学年高一下学期期末复习专题03 圆周运动的描述(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-06-11 21:00:49 | ||
图片预览




文档简介
专题03 圆周运动的描述
一、单选题
1.如图所示,拖拉机后轮的半径是前轮半径的两倍,A和B是前轮和后轮边缘上的点,若车行进时车轮没有打滑,则( )
A.两轮转动的周期相等
B.前轮和后轮的角速度之比为3:1
C.A点和B点的线速度大小之比为1:2
D.A点和B点的向心加速度大小之比为2:1
2.对于做匀速圆周运动的物体,下列说法中正确的是( )
A.线速度不变 B.周期变化
C.角速度大小不变 D.运动状态不变
3.如图所示,带有一白点的黑色圆盘,绕过其中心且垂直于盘面的轴沿顺时针方向匀速转动,转速为20r/s。在暗室中用每秒闪光25次的频闪光源照射圆盘,则观察到白点转动方向和转动周期分别为( )
A.逆时针转动,周期为0.2s
B.顺时针转动,周期为0.2s
C.逆时针转动,周期为1s
D.顺时针转动,周期为1s
4.在粗糙水平木板上放一个物块,沿逆时针方向做匀速圆周运动,ab为水平直径,cd为竖直直径,在运动中木板始终保持水平,物块相对于木板始终静止,下列说法正确的是( )
A.物块始终受到三个力的作用
B.只有在a、b、c、d四点,物块受到的合外力才指向圆心
C.从a到b,物块处于超重状态
D.从b到d,物块处于超重状态
5.如图所示,内壁光滑的圆锥筒的轴线垂直于水平面,圆锥筒固定不动,两个质量不同的小球A和B紧贴着内壁分别在如图所示的水平面内做匀速圆周运动,则( )
A.球A的线速度一定小于球B的线速度
B.球A的角速度一定大于球B的角速度
C.球A的向心加速度一定等于球B的向心加速度
D.球A对筒壁的压力一定等于球B对筒壁的压力
6.如图所示,半径分别为R和2R的两个转盘A、B处于水平面内,两者边缘紧密接触,靠静摩擦传动,均可以绕竖直方向的转轴O1及O2转动,两个转盘A、B始终不打滑。一个滑块(视为质点,图中未画出)放在转盘A上,离O1的距离为,已知滑块与转盘间的动摩擦因数为μ,重力加速度大小为g,滑动摩擦力等于最大静摩擦力。现使转盘B的转速逐渐增大,要使滑块不滑动,转盘B的角速度的最大值为( )
A. B. C. D.
7.如图所示,某同学用硬塑料管和一个质量为m的铁质螺丝帽研究匀速圆周运动,将螺丝帽套在塑料管上,手握塑料管使其保持竖直并在水平方向做半径为r的匀速圆周运动,则只要运动角速度合适,螺丝帽恰好不下滑,假设螺丝帽与塑料管间的动摩擦因数为μ,认为最大静摩擦力近似等于滑动摩擦力.则在该同学手转塑料管使螺丝帽恰好不下滑时,下述分析正确的是
A.螺丝帽受到的静摩擦力提供向心力
B.螺丝帽的线速度大小为
C.若杆的转动加快,螺丝帽有可能相对杆向上运动
D.若螺丝帽的质量变为原来的2倍,则转动的角速度至少要变成原来倍才能使其在原来轨道做圆周运动
8.明代出版的《天工开物》一书中,有牛力齿轮(牛转翻车)的图画,如图所示,这说明勤劳勇敢的先辈们已经掌握了齿轮传动技术。A、B两轮边缘质点做匀速圆周运动的半径分别为、,A、B两轮边缘的齿轮数分别为、,在两轮转动过程中(不打滑),下列说法正确的是( )
A.A、B两轮边缘质点的线速度大小之比
B.A、B两轮的转速之比
C.A、B两轮的角速度
D.A、B两轮边缘质点的向心加速度大小之比
二、多选题
9.如图所示,正在水平面内旋转的圆盘上有a、b两点,则( )
A.两点的线速度 B.两点的线速度
C.两点的角速度 D.两点的角速度
10.木块随圆桶绕轴线做匀速圆周运动( )
A.木块受重力、筒壁的弹力和摩擦力、离心力的作用
B.圆桶做匀速圆周运动的转速越大桶壁对木块的摩擦力越大
C.木块随筒壁做匀速圆周运动时的向心力由桶壁的弹力提供
D.桶壁对木块的弹力随着转速的增大而增大
11.如图所示,一个圆环绕中心线AB以一定的角速度转动,下列说法正确
A.P、Q两点的线速度相同 B.P、Q两点的角速度相同
C.P、Q两点的线速度之比为:l D.P、Q两点的角速度之比为:1
12.下雨天,同学间会经常转动并甩落雨伞边缘的雨点嬉闹。某次,甲同学沿竖直方向上打着一把雨伞,伞边缘离伞柄的距离,离地面的高度为,旁边有一位乙同学,身高,离伞边缘的最小水平距离为,甲同学要想把雨点甩到乙同学身上,则转动雨伞的角速度可能是(取)( )
A. B. C. D.
三、实验题
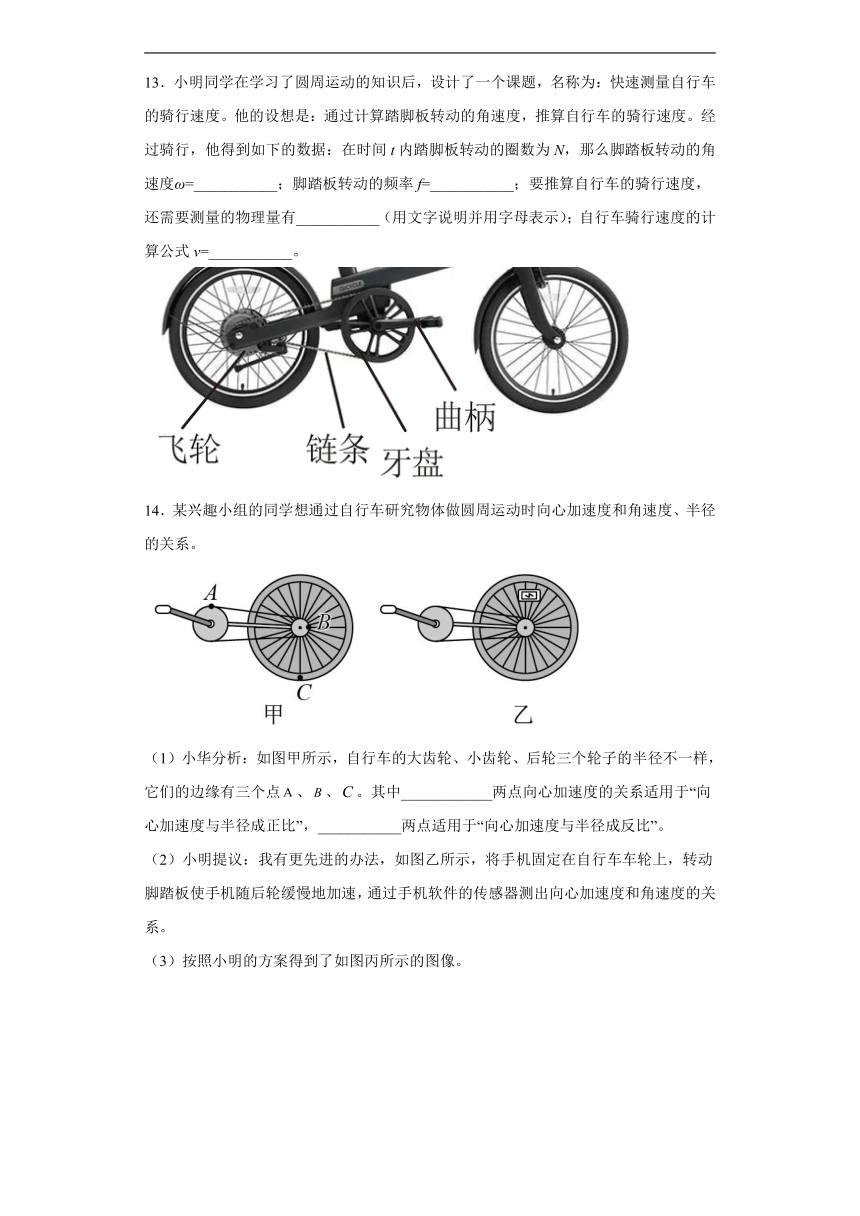
13.小明同学在学习了圆周运动的知识后,设计了一个课题,名称为:快速测量自行车的骑行速度。他的设想是:通过计算踏脚板转动的角速度,推算自行车的骑行速度。经过骑行,他得到如下的数据:在时间t内踏脚板转动的圈数为N,那么脚踏板转动的角速度ω=___________;脚踏板转动的频率f=___________;要推算自行车的骑行速度,还需要测量的物理量有___________(用文字说明并用字母表示);自行车骑行速度的计算公式v=___________。
14.某兴趣小组的同学想通过自行车研究物体做圆周运动时向心加速度和角速度、半径的关系。
(1)小华分析:如图甲所示,自行车的大齿轮、小齿轮、后轮三个轮子的半径不一样,它们的边缘有三个点、、。其中____________两点向心加速度的关系适用于“向心加速度与半径成正比”,___________两点适用于“向心加速度与半径成反比”。
(2)小明提议:我有更先进的办法,如图乙所示,将手机固定在自行车车轮上,转动脚踏板使手机随后轮缓慢地加速,通过手机软件的传感器测出向心加速度和角速度的关系。
(3)按照小明的方案得到了如图丙所示的图像。
①仅由图丙中的曲线可以得到的结论是:半径一定时,角速度越大,向心加速度越__________;
②为了研究向心加速度和角速度的定量关系,小明把坐标改为,多次实验均得到一条过原点的直线,如图丁所示,说明____________________;
③若要研究向心加速度与半径的关系,应该保持__________不变,改变____________,通过软件记录向心加速度的大小。
四、解答题
15.对于做匀速圆周运动的两个物体,下列说法是否正确?试说明理由。
(1)角速度大的物体,线速度也一定大;
(2)周期大的物体,角速度也一定大。
16.如图所示,由于地球自转,地球上的一切物体都随地球一起转动,现有A、B两人,A在赤道上,B在北纬60°处,A、B两人的角速度、线速度分别是多少?(地球半径R=6400km)
17.某同学在乘坐公交车时发现,在加速和转弯过程中,公交车里的扶手会发生偏转。为了研究这一现象,该同学在公交车的横杆上用长度为l的轻质细绳悬挂一个质量为m的小球(可看作质点),在公交车行驶过程中,进行观察和记录:
①沿平直的公路匀加速运动,细绳向后偏离竖直方向角度为θ1,在此状态下的某一时刻,通过汽车的仪表盘读出汽车的速度大小为v1;
②沿圆弧道路匀速转弯的过程中,细绳向圆弧轨道外侧偏离竖直方向角度为,通过汽车的仪表盘读出此过程中汽车的速度大小为v2。
(1)求汽车在①过程中的加速度;
(2)在①的情况下,从静止开始到速度为v1过程中,细绳的拉力对小球是否做功?如果做功,求出细绳对小球做功的大小;如果不做功,请说明理由;
(3)在②过程中,求公交车转弯的半径。并通过计算分析若缩短绳长,细绳偏离竖直方向的角度如何变化。
18.很多青少年在山地自行车上安装了气门嘴灯,夜间骑车时犹如踏着风火轮,格外亮眼。如图甲是某种自行车气门嘴灯,气门嘴灯内部开关结构如图乙所示:弹簧一端固定,另一端与质量为m的小滑块(含触点a)连接,当触点a、b接触,电路接通使气门嘴灯发光,触点b位于车轮边缘。车轮静止且气门嘴灯在最低点时触点a、b距离为L,弹簧劲度系数为,重力加速度大小为g,自行车轮胎半径为R,不计开关中的一切摩擦,滑块和触点a、b均可视为质点。
(1)若自行车匀速行驶过程中气门嘴灯可以一直亮,求自行车行驶的最小速度;
(2)若自行车以的速度匀速行驶,求车轮每转一圈,气门嘴灯的发光时间。
参考答案:
1.D
【详解】B.根据v=ωr和vA=vB , 可知A、B两点的角速度之比为2:1;故B不正确;
A.据可得前轮与后轮的角速度之比2:1,求得两轮的转动周期为1:2,故A错误;
C.轮A、B分别为同一传动装置前轮和后轮边缘上的一点,所以vA=vB , 故C错误;
D.由,可知向心加速度与半径成反比,则A与B点的向心加速度之比为2:1,故D正确。
故选D。
2.C
【详解】A.做匀速圆周运动的物体线速度大小不变,方向变化,故A错误;
BC.做匀速圆周运动的物体,周期、角速度不变,故B错误,C正确;
D.由于物体的线速度方向变化,故其运动状态发生变化,故D错误;
故选C。
3.A
【详解】白点做匀速圆周运动,每秒沿顺时针方向旋转20圈,在1s内比频闪光源少转5圈,因此观察到白点的转动方向为逆时针;白点每隔回到出发点,而闪光灯每隔闪光次,假设至少经过时间t白点刚好回到出发点而闪光灯刚好闪光,即刚好是和的最小公倍数,则有
t=0.2s
即周期为0.2s,A正确,BCD错误。
故选A。
4.D
【详解】B.物块做匀速圆周运动,合外力提供向心力,方向指向圆心,任何位置都是如此,故B错误;
A.在最高点和最低点,合力指向圆心,水平方向合力0,因此摩擦力等于0,重力和支持力的合力提供向心力,所以并不是始终受到三个力的作用,故A错误;
CD.从a到b,竖直方向分加速度竖直向下,属于失重状态;从b到a加速度指向圆心,竖直方向分加速度竖直向上,属于超重状态。故C错误,D正确。
故选D。
5.C
【详解】ABC.对小球受力分析,小球受到重力和支持力,它们的合力提供向心力,如图:
根据牛顿第二定律,有
解得
A的半径大,则A的线速度大,角速度小,向心加速度相等,故C正确,AB错误;
D.因为支持力
根据题意,两小球的质量不同,故支持力不相等,故D错误。
故选C。
6.B
【详解】两转盘边缘线速度相等,根据
两转盘角速度之比为
滑块恰好不滑动时
转盘B的角速度的最大值
得
故选B。
7.B
【详解】A、螺丝帽恰好不下滑,知螺丝帽受到重力和最大静摩擦力平衡,螺丝帽在水平方向受到的弹力提供向心力,弹力的方向指向圆心,故选项A错误;
BD、根据,解得,根据,解得线速度大小为,角速度大小为,角速度大小与质量无关,故选项B正确,D错误.
C、若杆转动加快,则向心力增大,弹力增大,最大静摩擦力增大,螺丝帽受重力和静摩擦力仍然平衡,故选项C错误.
8.B
【详解】A.A、B两轮是齿轮传动,边缘点线速度大小相等,故A错误;
B.两轮的周期之比
转速
所以两轮的转速之比
故B正确;
C.由公式可知,两轮的角速度
故C错误;
D.由可知
故D错误。
故选B。
9.BC
【详解】本题主要考查线速度、角速度。共轴转动的点,角速度大小相等,根据比较各点的线速度大小。
a、b共轴转动,角速度相同,a点的半径大于b点的半径,根据知,a点的线速度大于b点的线速度,故BC正确,AD错误;
故选BC。
10.CD
【详解】A.木块受重力、筒壁的弹力和摩擦力,没有离心力,故A错误;
B.桶壁对木块的摩擦力与木块本身的重力是一对平衡力,则圆桶做匀速圆周运动的转速越大桶壁对木块的摩擦力不变,故B错误;
C.木块随筒壁做匀速圆周运动时的向心力由桶壁的弹力提供,故C正确;
D.根据牛顿第二定律可知
则桶壁对木块的弹力随着转速的增大而增大,故D正确。
故选CD。
11.BC
【详解】AB.P、Q两点同轴转动,角速度相同,但两点到AB的距离不同,即轨道半径不同,根据可得两点的线速度不同,A错误B正确;
CD.因为,,转动的半径之比为,根据知,P、Q两点的线速度之比,C正确D错误.
故选BC.
【点睛】解决本题的关键知道共轴转动的点角速度大小相等,同一条皮带相连的点的线速度大小相等.
12.BC
【详解】设伞的半径是,乙同学离伞边缘的最小水平距离为,雨点甩到乙同学身上,则雨滴的平抛的水平位移为
转动雨伞的角速度ω,雨滴离开伞时的速度大小为
雨滴做平抛运动,有
则雨滴的水平位移
正好落在乙同学头上时,雨滴下落 ,解得
正好落在乙同学脚上时,雨滴下落 ,解得
则转动雨伞的角速度可能是和。
故选BC。
13. 车轮的半径R,牙盘的齿轮数m、飞轮的齿轮数n
【详解】[1][2] 脚踏板转动的频率
角速度
[3][4]根据车轮的线速度
v=ω0R
可知,要得到骑行速度还需要测量车轮的半径R,牙盘的齿轮数m、飞轮的齿轮数n,其中牙盘线速度与飞轮线速度相同
所以线速度
14. BC AB 大 半径一定时,向心加速度与角速度平方成正比 角速度 半径大小
【详解】(1)[1][2]其中BC两点同轴转动,角速度相同,根据
a=ω2r
则BC两点向心加速度的关系适用于“向心加速度与半径成正比”;因AB两点的线速度相同,则根据
可知,AB两点适用于“向心加速度与半径成反比”。
(3)①[3]仅由图丙中的曲线可以得到的结论是:半径一定时,角速度越大,向心加速度越大;
②[4]为了研究向心加速度和角速度的定量关系,小明把坐标改为,多次实验均得到一条过原点的直线,如图丁所示,说明半径一定时,向心加速度与角速度平方成正比;
③[5][6]若要研究向心加速度与半径的关系,应该保持角速度不变,改变半径大小,通过软件记录向心加速度的大小。
15.(1)错误;(2)错误
【详解】(1)由公式
可知只有r一定的情况下,速度大的物体,线速度才一定大,题中未给出r一定,故该说法错误;
(2)由公式
可知周期大的物体,角速度也一定小,题中“周期大的物体,角速度也一定大”的说法错误。
16.;;
【详解】A、B两人随地球自转,做圆周运动的周期相同,均等于地球自转的周期,但两人做圆周运动的圆周、圆心的位置及轨道半径不同。A、B两人的角速度相等,均等于地球的自转角速度
由得
17.(1) ,(2)做功,;(3),θ变小
【详解】(1)由受力分析可知:重力与细绳拉力的合力
根据牛顿第二定律
可知
(2)细绳的拉力做功,由动能定理
可得
(3)由受力分析可知:重力与细绳拉力的合力
匀速转弯时向心力
解得
可得
由单调性可得绳长l变小,θ变小
18.(1);(2)
【详解】(1)只要气嘴灯位于最高点时ab接触即可保证全程灯亮,弹簧原长时ab的距离为
气嘴灯位于最高点时的向心力为
可解得满足要求的最小速度为
(2)速度为时轮子滚动的周期为
此速度下气嘴灯所需的向心力为
此力恰好等于ab接触时弹簧的弹力,即无重力参与向心力,对应与圆心等高的点,故当气嘴灯位于下半圆周时灯亮,即
一、单选题
1.如图所示,拖拉机后轮的半径是前轮半径的两倍,A和B是前轮和后轮边缘上的点,若车行进时车轮没有打滑,则( )
A.两轮转动的周期相等
B.前轮和后轮的角速度之比为3:1
C.A点和B点的线速度大小之比为1:2
D.A点和B点的向心加速度大小之比为2:1
2.对于做匀速圆周运动的物体,下列说法中正确的是( )
A.线速度不变 B.周期变化
C.角速度大小不变 D.运动状态不变
3.如图所示,带有一白点的黑色圆盘,绕过其中心且垂直于盘面的轴沿顺时针方向匀速转动,转速为20r/s。在暗室中用每秒闪光25次的频闪光源照射圆盘,则观察到白点转动方向和转动周期分别为( )
A.逆时针转动,周期为0.2s
B.顺时针转动,周期为0.2s
C.逆时针转动,周期为1s
D.顺时针转动,周期为1s
4.在粗糙水平木板上放一个物块,沿逆时针方向做匀速圆周运动,ab为水平直径,cd为竖直直径,在运动中木板始终保持水平,物块相对于木板始终静止,下列说法正确的是( )
A.物块始终受到三个力的作用
B.只有在a、b、c、d四点,物块受到的合外力才指向圆心
C.从a到b,物块处于超重状态
D.从b到d,物块处于超重状态
5.如图所示,内壁光滑的圆锥筒的轴线垂直于水平面,圆锥筒固定不动,两个质量不同的小球A和B紧贴着内壁分别在如图所示的水平面内做匀速圆周运动,则( )
A.球A的线速度一定小于球B的线速度
B.球A的角速度一定大于球B的角速度
C.球A的向心加速度一定等于球B的向心加速度
D.球A对筒壁的压力一定等于球B对筒壁的压力
6.如图所示,半径分别为R和2R的两个转盘A、B处于水平面内,两者边缘紧密接触,靠静摩擦传动,均可以绕竖直方向的转轴O1及O2转动,两个转盘A、B始终不打滑。一个滑块(视为质点,图中未画出)放在转盘A上,离O1的距离为,已知滑块与转盘间的动摩擦因数为μ,重力加速度大小为g,滑动摩擦力等于最大静摩擦力。现使转盘B的转速逐渐增大,要使滑块不滑动,转盘B的角速度的最大值为( )
A. B. C. D.
7.如图所示,某同学用硬塑料管和一个质量为m的铁质螺丝帽研究匀速圆周运动,将螺丝帽套在塑料管上,手握塑料管使其保持竖直并在水平方向做半径为r的匀速圆周运动,则只要运动角速度合适,螺丝帽恰好不下滑,假设螺丝帽与塑料管间的动摩擦因数为μ,认为最大静摩擦力近似等于滑动摩擦力.则在该同学手转塑料管使螺丝帽恰好不下滑时,下述分析正确的是
A.螺丝帽受到的静摩擦力提供向心力
B.螺丝帽的线速度大小为
C.若杆的转动加快,螺丝帽有可能相对杆向上运动
D.若螺丝帽的质量变为原来的2倍,则转动的角速度至少要变成原来倍才能使其在原来轨道做圆周运动
8.明代出版的《天工开物》一书中,有牛力齿轮(牛转翻车)的图画,如图所示,这说明勤劳勇敢的先辈们已经掌握了齿轮传动技术。A、B两轮边缘质点做匀速圆周运动的半径分别为、,A、B两轮边缘的齿轮数分别为、,在两轮转动过程中(不打滑),下列说法正确的是( )
A.A、B两轮边缘质点的线速度大小之比
B.A、B两轮的转速之比
C.A、B两轮的角速度
D.A、B两轮边缘质点的向心加速度大小之比
二、多选题
9.如图所示,正在水平面内旋转的圆盘上有a、b两点,则( )
A.两点的线速度 B.两点的线速度
C.两点的角速度 D.两点的角速度
10.木块随圆桶绕轴线做匀速圆周运动( )
A.木块受重力、筒壁的弹力和摩擦力、离心力的作用
B.圆桶做匀速圆周运动的转速越大桶壁对木块的摩擦力越大
C.木块随筒壁做匀速圆周运动时的向心力由桶壁的弹力提供
D.桶壁对木块的弹力随着转速的增大而增大
11.如图所示,一个圆环绕中心线AB以一定的角速度转动,下列说法正确
A.P、Q两点的线速度相同 B.P、Q两点的角速度相同
C.P、Q两点的线速度之比为:l D.P、Q两点的角速度之比为:1
12.下雨天,同学间会经常转动并甩落雨伞边缘的雨点嬉闹。某次,甲同学沿竖直方向上打着一把雨伞,伞边缘离伞柄的距离,离地面的高度为,旁边有一位乙同学,身高,离伞边缘的最小水平距离为,甲同学要想把雨点甩到乙同学身上,则转动雨伞的角速度可能是(取)( )
A. B. C. D.
三、实验题
13.小明同学在学习了圆周运动的知识后,设计了一个课题,名称为:快速测量自行车的骑行速度。他的设想是:通过计算踏脚板转动的角速度,推算自行车的骑行速度。经过骑行,他得到如下的数据:在时间t内踏脚板转动的圈数为N,那么脚踏板转动的角速度ω=___________;脚踏板转动的频率f=___________;要推算自行车的骑行速度,还需要测量的物理量有___________(用文字说明并用字母表示);自行车骑行速度的计算公式v=___________。
14.某兴趣小组的同学想通过自行车研究物体做圆周运动时向心加速度和角速度、半径的关系。
(1)小华分析:如图甲所示,自行车的大齿轮、小齿轮、后轮三个轮子的半径不一样,它们的边缘有三个点、、。其中____________两点向心加速度的关系适用于“向心加速度与半径成正比”,___________两点适用于“向心加速度与半径成反比”。
(2)小明提议:我有更先进的办法,如图乙所示,将手机固定在自行车车轮上,转动脚踏板使手机随后轮缓慢地加速,通过手机软件的传感器测出向心加速度和角速度的关系。
(3)按照小明的方案得到了如图丙所示的图像。
①仅由图丙中的曲线可以得到的结论是:半径一定时,角速度越大,向心加速度越__________;
②为了研究向心加速度和角速度的定量关系,小明把坐标改为,多次实验均得到一条过原点的直线,如图丁所示,说明____________________;
③若要研究向心加速度与半径的关系,应该保持__________不变,改变____________,通过软件记录向心加速度的大小。
四、解答题
15.对于做匀速圆周运动的两个物体,下列说法是否正确?试说明理由。
(1)角速度大的物体,线速度也一定大;
(2)周期大的物体,角速度也一定大。
16.如图所示,由于地球自转,地球上的一切物体都随地球一起转动,现有A、B两人,A在赤道上,B在北纬60°处,A、B两人的角速度、线速度分别是多少?(地球半径R=6400km)
17.某同学在乘坐公交车时发现,在加速和转弯过程中,公交车里的扶手会发生偏转。为了研究这一现象,该同学在公交车的横杆上用长度为l的轻质细绳悬挂一个质量为m的小球(可看作质点),在公交车行驶过程中,进行观察和记录:
①沿平直的公路匀加速运动,细绳向后偏离竖直方向角度为θ1,在此状态下的某一时刻,通过汽车的仪表盘读出汽车的速度大小为v1;
②沿圆弧道路匀速转弯的过程中,细绳向圆弧轨道外侧偏离竖直方向角度为,通过汽车的仪表盘读出此过程中汽车的速度大小为v2。
(1)求汽车在①过程中的加速度;
(2)在①的情况下,从静止开始到速度为v1过程中,细绳的拉力对小球是否做功?如果做功,求出细绳对小球做功的大小;如果不做功,请说明理由;
(3)在②过程中,求公交车转弯的半径。并通过计算分析若缩短绳长,细绳偏离竖直方向的角度如何变化。
18.很多青少年在山地自行车上安装了气门嘴灯,夜间骑车时犹如踏着风火轮,格外亮眼。如图甲是某种自行车气门嘴灯,气门嘴灯内部开关结构如图乙所示:弹簧一端固定,另一端与质量为m的小滑块(含触点a)连接,当触点a、b接触,电路接通使气门嘴灯发光,触点b位于车轮边缘。车轮静止且气门嘴灯在最低点时触点a、b距离为L,弹簧劲度系数为,重力加速度大小为g,自行车轮胎半径为R,不计开关中的一切摩擦,滑块和触点a、b均可视为质点。
(1)若自行车匀速行驶过程中气门嘴灯可以一直亮,求自行车行驶的最小速度;
(2)若自行车以的速度匀速行驶,求车轮每转一圈,气门嘴灯的发光时间。
参考答案:
1.D
【详解】B.根据v=ωr和vA=vB , 可知A、B两点的角速度之比为2:1;故B不正确;
A.据可得前轮与后轮的角速度之比2:1,求得两轮的转动周期为1:2,故A错误;
C.轮A、B分别为同一传动装置前轮和后轮边缘上的一点,所以vA=vB , 故C错误;
D.由,可知向心加速度与半径成反比,则A与B点的向心加速度之比为2:1,故D正确。
故选D。
2.C
【详解】A.做匀速圆周运动的物体线速度大小不变,方向变化,故A错误;
BC.做匀速圆周运动的物体,周期、角速度不变,故B错误,C正确;
D.由于物体的线速度方向变化,故其运动状态发生变化,故D错误;
故选C。
3.A
【详解】白点做匀速圆周运动,每秒沿顺时针方向旋转20圈,在1s内比频闪光源少转5圈,因此观察到白点的转动方向为逆时针;白点每隔回到出发点,而闪光灯每隔闪光次,假设至少经过时间t白点刚好回到出发点而闪光灯刚好闪光,即刚好是和的最小公倍数,则有
t=0.2s
即周期为0.2s,A正确,BCD错误。
故选A。
4.D
【详解】B.物块做匀速圆周运动,合外力提供向心力,方向指向圆心,任何位置都是如此,故B错误;
A.在最高点和最低点,合力指向圆心,水平方向合力0,因此摩擦力等于0,重力和支持力的合力提供向心力,所以并不是始终受到三个力的作用,故A错误;
CD.从a到b,竖直方向分加速度竖直向下,属于失重状态;从b到a加速度指向圆心,竖直方向分加速度竖直向上,属于超重状态。故C错误,D正确。
故选D。
5.C
【详解】ABC.对小球受力分析,小球受到重力和支持力,它们的合力提供向心力,如图:
根据牛顿第二定律,有
解得
A的半径大,则A的线速度大,角速度小,向心加速度相等,故C正确,AB错误;
D.因为支持力
根据题意,两小球的质量不同,故支持力不相等,故D错误。
故选C。
6.B
【详解】两转盘边缘线速度相等,根据
两转盘角速度之比为
滑块恰好不滑动时
转盘B的角速度的最大值
得
故选B。
7.B
【详解】A、螺丝帽恰好不下滑,知螺丝帽受到重力和最大静摩擦力平衡,螺丝帽在水平方向受到的弹力提供向心力,弹力的方向指向圆心,故选项A错误;
BD、根据,解得,根据,解得线速度大小为,角速度大小为,角速度大小与质量无关,故选项B正确,D错误.
C、若杆转动加快,则向心力增大,弹力增大,最大静摩擦力增大,螺丝帽受重力和静摩擦力仍然平衡,故选项C错误.
8.B
【详解】A.A、B两轮是齿轮传动,边缘点线速度大小相等,故A错误;
B.两轮的周期之比
转速
所以两轮的转速之比
故B正确;
C.由公式可知,两轮的角速度
故C错误;
D.由可知
故D错误。
故选B。
9.BC
【详解】本题主要考查线速度、角速度。共轴转动的点,角速度大小相等,根据比较各点的线速度大小。
a、b共轴转动,角速度相同,a点的半径大于b点的半径,根据知,a点的线速度大于b点的线速度,故BC正确,AD错误;
故选BC。
10.CD
【详解】A.木块受重力、筒壁的弹力和摩擦力,没有离心力,故A错误;
B.桶壁对木块的摩擦力与木块本身的重力是一对平衡力,则圆桶做匀速圆周运动的转速越大桶壁对木块的摩擦力不变,故B错误;
C.木块随筒壁做匀速圆周运动时的向心力由桶壁的弹力提供,故C正确;
D.根据牛顿第二定律可知
则桶壁对木块的弹力随着转速的增大而增大,故D正确。
故选CD。
11.BC
【详解】AB.P、Q两点同轴转动,角速度相同,但两点到AB的距离不同,即轨道半径不同,根据可得两点的线速度不同,A错误B正确;
CD.因为,,转动的半径之比为,根据知,P、Q两点的线速度之比,C正确D错误.
故选BC.
【点睛】解决本题的关键知道共轴转动的点角速度大小相等,同一条皮带相连的点的线速度大小相等.
12.BC
【详解】设伞的半径是,乙同学离伞边缘的最小水平距离为,雨点甩到乙同学身上,则雨滴的平抛的水平位移为
转动雨伞的角速度ω,雨滴离开伞时的速度大小为
雨滴做平抛运动,有
则雨滴的水平位移
正好落在乙同学头上时,雨滴下落 ,解得
正好落在乙同学脚上时,雨滴下落 ,解得
则转动雨伞的角速度可能是和。
故选BC。
13. 车轮的半径R,牙盘的齿轮数m、飞轮的齿轮数n
【详解】[1][2] 脚踏板转动的频率
角速度
[3][4]根据车轮的线速度
v=ω0R
可知,要得到骑行速度还需要测量车轮的半径R,牙盘的齿轮数m、飞轮的齿轮数n,其中牙盘线速度与飞轮线速度相同
所以线速度
14. BC AB 大 半径一定时,向心加速度与角速度平方成正比 角速度 半径大小
【详解】(1)[1][2]其中BC两点同轴转动,角速度相同,根据
a=ω2r
则BC两点向心加速度的关系适用于“向心加速度与半径成正比”;因AB两点的线速度相同,则根据
可知,AB两点适用于“向心加速度与半径成反比”。
(3)①[3]仅由图丙中的曲线可以得到的结论是:半径一定时,角速度越大,向心加速度越大;
②[4]为了研究向心加速度和角速度的定量关系,小明把坐标改为,多次实验均得到一条过原点的直线,如图丁所示,说明半径一定时,向心加速度与角速度平方成正比;
③[5][6]若要研究向心加速度与半径的关系,应该保持角速度不变,改变半径大小,通过软件记录向心加速度的大小。
15.(1)错误;(2)错误
【详解】(1)由公式
可知只有r一定的情况下,速度大的物体,线速度才一定大,题中未给出r一定,故该说法错误;
(2)由公式
可知周期大的物体,角速度也一定小,题中“周期大的物体,角速度也一定大”的说法错误。
16.;;
【详解】A、B两人随地球自转,做圆周运动的周期相同,均等于地球自转的周期,但两人做圆周运动的圆周、圆心的位置及轨道半径不同。A、B两人的角速度相等,均等于地球的自转角速度
由得
17.(1) ,(2)做功,;(3),θ变小
【详解】(1)由受力分析可知:重力与细绳拉力的合力
根据牛顿第二定律
可知
(2)细绳的拉力做功,由动能定理
可得
(3)由受力分析可知:重力与细绳拉力的合力
匀速转弯时向心力
解得
可得
由单调性可得绳长l变小,θ变小
18.(1);(2)
【详解】(1)只要气嘴灯位于最高点时ab接触即可保证全程灯亮,弹簧原长时ab的距离为
气嘴灯位于最高点时的向心力为
可解得满足要求的最小速度为
(2)速度为时轮子滚动的周期为
此速度下气嘴灯所需的向心力为
此力恰好等于ab接触时弹簧的弹力,即无重力参与向心力,对应与圆心等高的点,故当气嘴灯位于下半圆周时灯亮,即
同课章节目录
