2023年广东省中考数学考前热身训练(三)(含解析)
文档属性
| 名称 | 2023年广东省中考数学考前热身训练(三)(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 277.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-13 00:00:00 | ||
图片预览

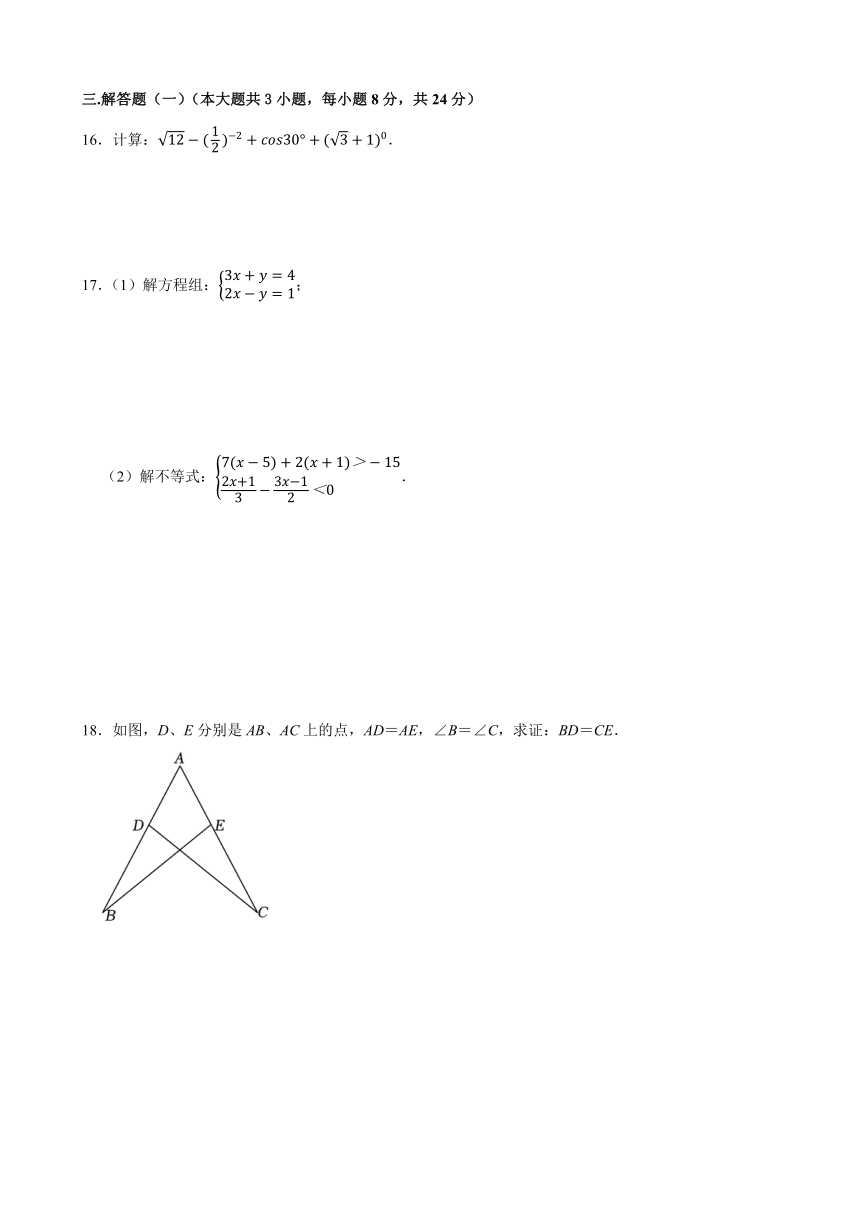

文档简介
2023年广东省中考数学考前热身(三)
一.选择题(共10小题,每小题3分,共30分)
1.﹣5的绝对值是( )
A.5 B.﹣5 C. D.
2.第108届全国糖酒会于2023年4月12~14日在成都市举办,本届糖酒会主题为“全国糖酒会会天下美味”,共设置10大展区及17个专区,展览总面积为32万平方米.将数据32万用科学记数法表示为( )
A.32×104 B.3.2×104 C.3.2×105 D.0.32×106
3.如图,直线l1∥l2,直线l3与l1,l2分别交于A,B两点,过点A作AC⊥l2,垂足为C,若∠1=52°,则∠2的度数是( )
A.32° B.38°
C.48° D.52°
4.下列运算正确的是( )
A. B.a÷a﹣2=a3 C. D.
5.在平面直角坐标系中,将点P(﹣4,﹣2)先向上平移3个单位长度,再向左平移2个单位长度后得到的点的坐标是( )
A.(﹣6,1) B.(﹣2,1) C.(﹣1,﹣4) D.(﹣1,0)
6.某小组7名学生的中考体育分数分别为55,55,57,58,60,60,60,该组数据的众数和中位数分别是( )
A.60,55 B.60,58 C.55,60 D.55,57
7.图为正方体的一种平面展开图,各面都标有数字,则数字为﹣4的面与其对面上的数字之积是( )
A.4 B.12
C.﹣4 D.0
8.关于x的一元二次方程kx2﹣2x0有两个不相等的实数根,则k的值不可能是( )
A.﹣2 B.﹣1 C.0 D.1
9.在△ABC中,D,E分别是边AB,AC上的两个点,并且DE∥BC,AD:BD=3:2,则△ADE与四边形BCED的面积之比为( )
A.3:5 B.4:25
C.9:16 D.9:25
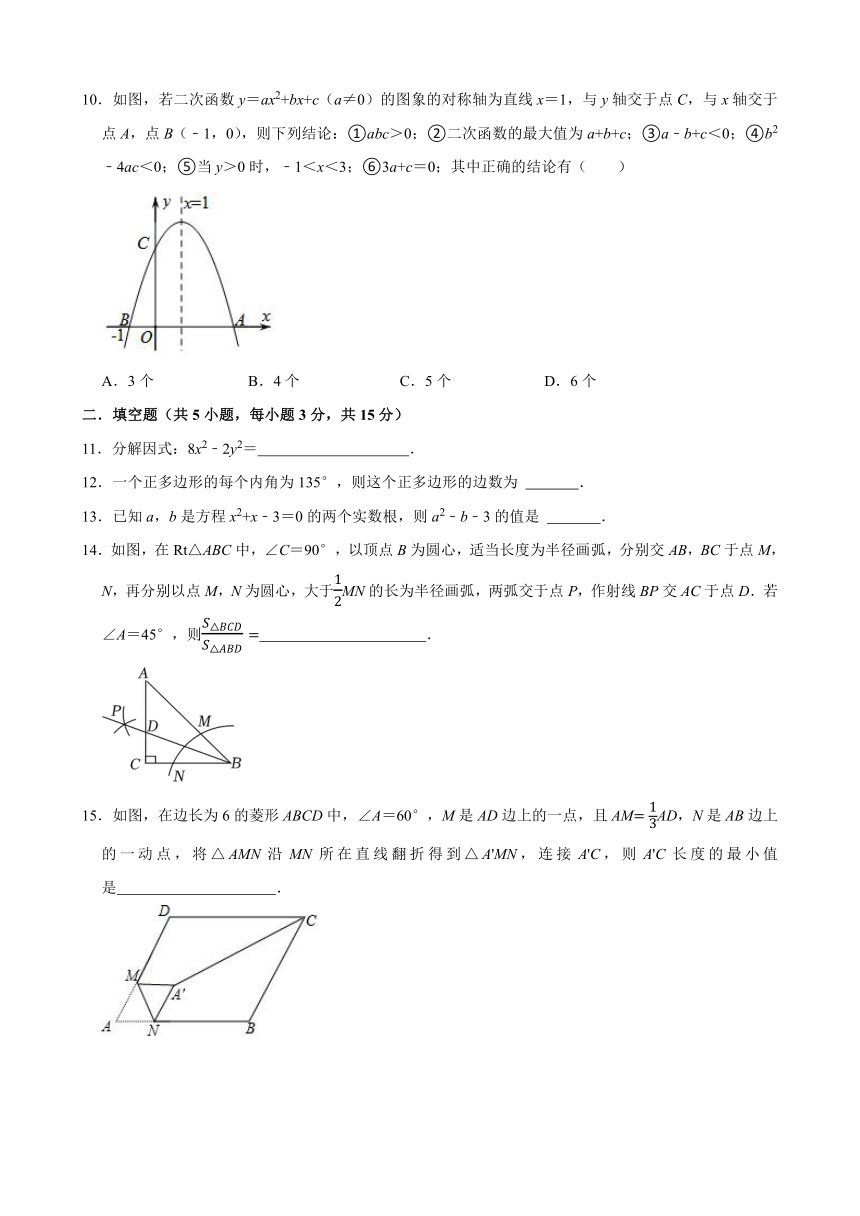
10.如图,若二次函数y=ax2+bx+c(a≠0)的图象的对称轴为直线x=1,与y轴交于点C,与x轴交于点A,点B(﹣1,0),则下列结论:①abc>0;②二次函数的最大值为a+b+c;③a﹣b+c<0;④b2﹣4ac<0;⑤当y>0时,﹣1<x<3;⑥3a+c=0;其中正确的结论有( )
A.3个 B.4个 C.5个 D.6个
二.填空题(共5小题,每小题3分,共15分)
11.分解因式:8x2﹣2y2= .
12.一个正多边形的每个内角为135°,则这个正多边形的边数为 .
13.已知a,b是方程x2+x﹣3=0的两个实数根,则a2﹣b﹣3的值是 .
14.如图,在Rt△ABC中,∠C=90°,以顶点B为圆心,适当长度为半径画弧,分别交AB,BC于点M,N,再分别以点M,N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线BP交AC于点D.若∠A=45°,则 .
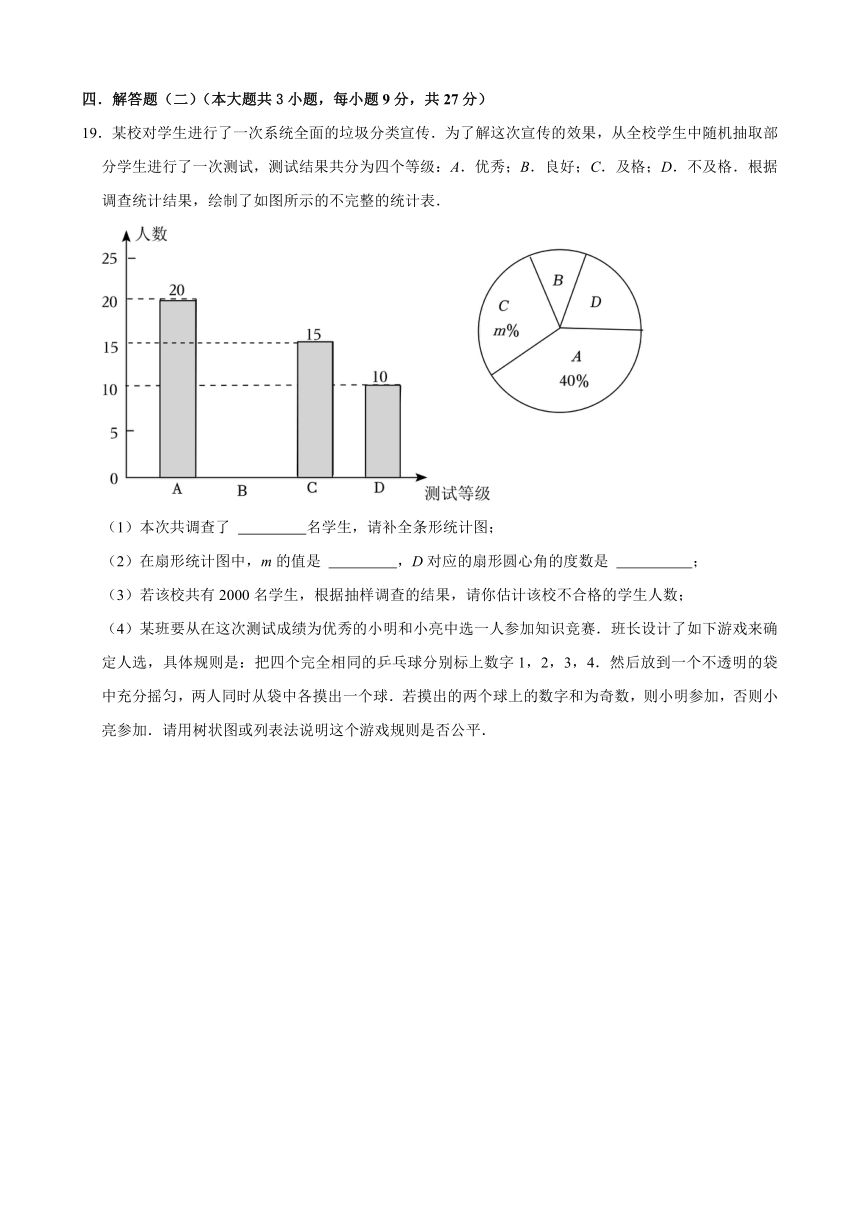
15.如图,在边长为6的菱形ABCD中,∠A=60°,M是AD边上的一点,且AMAD,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A'MN,连接A'C,则A'C长度的最小值是 .
三.解答题(一)(本大题共3小题,每小题8分,共24分)
16.计算:.
17.(1)解方程组:;
(2)解不等式:.
18.如图,D、E分别是AB、AC上的点,AD=AE,∠B=∠C,求证:BD=CE.
四.解答题(二)(本大题共3小题,每小题9分,共27分)
19.某校对学生进行了一次系统全面的垃圾分类宣传.为了解这次宣传的效果,从全校学生中随机抽取部分学生进行了一次测试,测试结果共分为四个等级:A.优秀;B.良好;C.及格;D.不及格.根据调查统计结果,绘制了如图所示的不完整的统计表.
(1)本次共调查了 名学生,请补全条形统计图;
(2)在扇形统计图中,m的值是 ,D对应的扇形圆心角的度数是 ;
(3)若该校共有2000名学生,根据抽样调查的结果,请你估计该校不合格的学生人数;
(4)某班要从在这次测试成绩为优秀的小明和小亮中选一人参加知识竞赛.班长设计了如下游戏来确定人选,具体规则是:把四个完全相同的乒乓球分别标上数字1,2,3,4.然后放到一个不透明的袋中充分摇匀,两人同时从袋中各摸出一个球.若摸出的两个球上的数字和为奇数,则小明参加,否则小亮参加.请用树状图或列表法说明这个游戏规则是否公平.
20.如图,在Rt△ABC中,∠ABC=90°,过点B作AC的平行线BD,使得BD=AB,连结AD交BC于点E,过点B作AD的垂线分别交AD,AC于点F,G,连结DG.
(1)求证:四边形ABDG是菱形.
(2)当EF=3,tan∠BGA=2时,求AC的长.
21.某校组织学生到某品牌运动鞋直销店参加社会实践活动,他们参与了该品牌运动鞋的销售工作,已知该运动鞋每双的成本价为130元,为寻求合适的销售价格进行了4天的试销,试销情况如下表所示:
第1天 第2天 第3天 第4天
售价x(元/双) 225 300 375 450
销售量y(双) 40 30 24 20
(1)观察表中数据,x,y满足什么函数关系?请求出这个函数关系式;
(2)在(1)的条件下,若直销店计划每天的销售利润为4500元,则其售价应定为多少元?
五.解答题(三)(本大题共2小题,每小题12分,共24分)
22.如图,在Rt△ABC中,∠ACB=90°,点D是AB的中点,以CD为直径作⊙O,与BC交于点E,过点E作⊙O的切线EF,交AB于点F.
(1)求证:EF⊥AB;
(2)若⊙O的半径是,,求DF的长.
23.如图1,在平面直角坐标系中,一次函数的图象分别交x,y轴于点A、B,抛物线经过点A、B,点P为第四象限内抛物线上的一个动点.
(1)写出点A、点B的坐标;
(2)求此抛物线对应的函数表达式;
(3)如图2,过点P作PM∥y轴,分别交直线AB、x轴于点C、D,若以点P、B、C为顶点的三角形与△ACD相似,求点P的坐标.
2023年广东省中考数学考前热身(三)
参考答案与试题解析
一.选择题(共10小题)
1.【解答】解:﹣5的绝对值等于5,
即|﹣5|=5.
故选:A.
2.【解答】解:32万=320000=3.2×105.
故选:C.
3.【解答】解:∵直线l1∥l2,∠1=52°,
∴∠ABC=∠1=52°,
∵AC⊥l2,
∴∠ACB=90°,
∴∠2=180°﹣∠ABC﹣∠ACB=180°﹣52°﹣90°=38°,
故选:B.
4.【解答】解:A、与不属于同类二次根式,不能运算,故A不符合题意;
B、a÷a﹣2=a3,故B符合题意;
C、,故C不符合题意;
D、,故D不符合题意;
故选:B.
5.【解答】解:点M(﹣4,﹣2)先向上平移3个单位,再向左平移2个单位,得到点N的坐标是(﹣4﹣2,﹣2+3),即(﹣6,1),
故选:A.
6.【解答】解:将7个数据按从小到大的顺序排列为55,55,57,58,60,60,60,
60出现了三次,次数最多,所以这组数据的众数为60,
中间的一个数是58,所以中位数为58.
故选:B.
7.【解答】解:数字为﹣4的面的对面上的数字是﹣3,其积为(﹣4)×(﹣3)=12.
故选:B.
8.【解答】解:∵关于x的一元二次方程kx2﹣2x0有两个不相等的实数根,
∴,
解得:k<2且k≠0,
∴k的值不可能是0.
故选:C.
9.【解答】解:∵AD:BD=3:2,
∴AD:AB=3:5,
∵DE∥BC,
∴△ADE∽△ABC,
∴()2=()2,
∴△ADE与四边形BCED的面积之比是9:16,
故选:C.
10.【解答】解:∵二次函数对称轴在y轴右侧,与y轴交在正半轴,
∴ab<0,c>0,abc<0.
∴故①不正确;
∵二次函数y=ax2+bx+c(a≠0)图象的对称轴为直线x=1,
∴顶点坐标为(1,a+b+c),且开口向下,二次函数的最大值为a+b+c,
故②正确;
∵抛物线过B(﹣1,0),
∴x=﹣1时,y=0,即a﹣b+c=0,
故③不正确;
∵抛物线与x轴有两个交点,
∴b2﹣4ac>0,
故④不正确;
∵对称轴为直线x=1,B(﹣1,0),
∴A(3,0),
由图象可知,﹣1<x<3时,y>0,
故⑤正确;
∵x1,即b=﹣2a,
而x=﹣1时,y=0,即a﹣b+c=0,
∴a+2a+c=0,
∴c+3a=0.
故⑥正确.
故选:A.
二.填空题(共5小题)
11.【解答】解:8x2﹣2y2
=2(4x2﹣y2)
=2(2x+y)(2x﹣y),
故答案为:2(2x+y)(2x﹣y).
12.【解答】解:180°﹣135°=45°,
360÷45=8.
故答案为:八.
13.【解答】解:∵a,b是方程x2+x﹣3=0的两个实数根,
∴a+b=﹣1,
把x=a代入方程得:a2+a﹣3=0,即a2=3﹣a,
则原式=3﹣a﹣b﹣3
=﹣(a+b)
=1.
故答案为:1.
14.【解答】解:由作法得BD平分∠ABC,
过D点作DH⊥AB于H点,如图,
∴DH=DC,
∴,
∵∠C=90°,∠A=45°,
∴△ABC为等腰直角三角形,
∴ABBC,
∴.
故答案为:.
15.【解答】解:如图,过点M作MH⊥CD交CD延长线于点H,连接CM,
∵AMAD,AD=CD=6,
∴AM=2,MD=4,
∵CD∥AB,
∴∠HDM=∠A=60°,
∴HDMD=2,HMHD,
∴CH=8,
∴MC,
∵将△AMN沿MN所在直线翻折得到△A′MN,
∴AM=A'M=2,
∴点A'在以M为圆心,AM为半径的圆上,
∴当点A'在线段MC上时,A'C长度有最小值,
∴A'C长度的最小值=MC﹣MA'2,
故答案为:2.
三.解答题(共8小题)
16.【解答】解:原式=241
3.
17.【解答】解:(1),
①+②,得:5x=5,
解得x=1,
将x=1代入①,得:3+y=4,
解得y=1,
∴方程组的解为;
(2)由7(x﹣5)+2(x+1)>﹣15,得:x>2,
由0,得:x>1,
则不等式组的解集为x>2.
18.【解答】证明:∵AD=AE,∠B=∠C,
又∠A=∠A,
在△ABE与△ACD中,
,
∴△ABE≌△ACD(AAS),
∴AB=AC,
∴AB﹣AD=AC﹣AE,
∴BD=CE.
19.【解答】解:(1)根据题意得:20÷40%=50(名),50﹣(20+15+10)=5(名),
补全条形统计图,如图所示:
故答案为:50;
(2)根据题意得:15÷50×100%=30%,即m=30,10÷50×360°=72°,
则在扇形统计图中,m的值是30,D对应的扇形圆心角的度数是72°;
故答案为:30,72°;
(3)根据题意得:2000400(名),
则估计该校不合格的学生人数约为400名;
(4)根据题意,列表如下:
1 2 3 4
1 ﹣﹣﹣﹣﹣﹣﹣﹣﹣ (1,2) (1,3) (1,4)
2 (2,1) ﹣﹣﹣﹣﹣﹣﹣﹣﹣ (2,3) (2,4)
3 (3,1) (3,2) ﹣﹣﹣﹣﹣﹣﹣﹣﹣ (3,4)
4 (4,1) (4,2) (4,3) ﹣﹣﹣﹣﹣﹣﹣﹣﹣
所有等可能的情况数有12种,其中和为奇数的有(1,2),(1,4),(2,1),(2,3),(3,2),(3,4),(4,1),(4,3),共8种,
∴P(小明参加),P(小亮参加)=1,
∵,
∴这个游戏规则不公平.
20.【解答】(1)证明:∵AB=BD,
∴△ABD是等腰三角形,
∵BG⊥AD,
∴AF=FD,
在△AFG与△DFG中,
,
∴△AFG≌△DFG(SAS),
∴AG=GD,∠AGF=∠DGF,
∵BD∥AC,
∴∠DBF=∠AGF,
∴∠DGF=∠DBF,
∴BD=DG,
∴AB=BD=DG=AG,
∴四边形ABDG是菱形;
(2)解:∵∠ABC=90°,
∴∠CBF+∠ABF=90°,
∵四边形ABDG是菱形,
∴∠ABF=∠BGA=∠DBG,
∵tan∠BGA=2,
∴tan∠ABF,
∴AF=2BF,
设BF=x,则AF=2x=DF,
∴ABx=BD,
∴AE=AF+EF=2x+3,
在Rt△BEF中,根据勾股定理得:BE2=BF2+EF2=x2+9,
在RtABE中,AB2+BE2=AE2,
∴(x)2+x2+9=(2x+3)2,
解得x=6或x=0(舍去),
∴BF=6,
∴AF=12,
∴AB=BD=6,AE=AF+EF=15,
∴DE=DF﹣EF=12﹣3=9,
∵BD∥AC,
∴△DBE∽△CAE,
∴,
∴,
∴AC=10.
∴AC的长为10.
21.【解答】解:(1)由表中的数据可得:xy=9000,
∴,
∴y是x的反比例函数,
所以这个函数关系式为;
(2)根据题意得:(x﹣130)y=4500,
将代入得,,
解得:x=260,
经检验,x=260是原方程的解且适合题意.
答:售价应定为260元.
22.【解答】(1)证明:连接OE,
∵∠ACB=90°,AD=DB,
∴DC=DB=DA,
∵CD是直径,
∴∠CFD=90°,即DE⊥BC,
∴CE=EB,
∵OC=OD,CE=BE,
∴OE是△CDB的中位线,
∴OE∥BD,
∴∠OEC=∠B,
∵EF是⊙O的切线,
∴∠OEF=90°,
∴∠OEC+∠BEF=90°,
∴∠BEF+∠B=90°,
∴∠EFB=90°,
∴EF⊥AB;
(2)解:连接DE,
在Rt△ABC中,
∵点D是AB的中点,CD=5,
∴AD=BD=5,
∴AB=10,
∵cos∠ACD,
∴AC=106,
∴BC8,
∵CD是⊙O的直径,
∴∠CED=90°,
∴BE=CEBC=4,
∴DE3,
∴S△BDEDE BEBD EF,
∴EF.
∴DF.
23.【解答】解:(1)令x=0,得2,则B(0,﹣2),
令0,解得x=4,则A(4,0),
(2)把A(4,0),B(0,﹣2)代入y=x2+bx+c(a≠0)中,
得,
解得.
∴抛物线的解析式为:y=x2x﹣2;
(3)∵PM∥y轴,
∴∠ADC=90°.
∵∠ACD=∠BCP,
∴以点P、B、C为顶点的三角形与以点A、C、D为顶点的三角形相似,存在两种情况:
①当∠CBP=90°时,如图,过P作PN⊥y轴于N,
∵∠ABO+∠PBN=∠ABO+∠OAB=90°,
∴∠PBN=∠OAB,
∵∠AOB=∠BNP=90°,
∴Rt△PBN∽Rt△BAO.
∴.
设P的坐标为(x,x2x﹣2).
∴,化简得.
解得x=0(舍去)或x.
∴P(,﹣5);
②当∠CPB=90°时,如图2,则PB∥x轴,所以B和P是对称点.
所以当y=﹣2时,则x2x﹣2=﹣2,解得x=0(舍去)或x.
∴P(,﹣2).
综上,点P的坐标(,﹣5)或(,﹣2).
一.选择题(共10小题,每小题3分,共30分)
1.﹣5的绝对值是( )
A.5 B.﹣5 C. D.
2.第108届全国糖酒会于2023年4月12~14日在成都市举办,本届糖酒会主题为“全国糖酒会会天下美味”,共设置10大展区及17个专区,展览总面积为32万平方米.将数据32万用科学记数法表示为( )
A.32×104 B.3.2×104 C.3.2×105 D.0.32×106
3.如图,直线l1∥l2,直线l3与l1,l2分别交于A,B两点,过点A作AC⊥l2,垂足为C,若∠1=52°,则∠2的度数是( )
A.32° B.38°
C.48° D.52°
4.下列运算正确的是( )
A. B.a÷a﹣2=a3 C. D.
5.在平面直角坐标系中,将点P(﹣4,﹣2)先向上平移3个单位长度,再向左平移2个单位长度后得到的点的坐标是( )
A.(﹣6,1) B.(﹣2,1) C.(﹣1,﹣4) D.(﹣1,0)
6.某小组7名学生的中考体育分数分别为55,55,57,58,60,60,60,该组数据的众数和中位数分别是( )
A.60,55 B.60,58 C.55,60 D.55,57
7.图为正方体的一种平面展开图,各面都标有数字,则数字为﹣4的面与其对面上的数字之积是( )
A.4 B.12
C.﹣4 D.0
8.关于x的一元二次方程kx2﹣2x0有两个不相等的实数根,则k的值不可能是( )
A.﹣2 B.﹣1 C.0 D.1
9.在△ABC中,D,E分别是边AB,AC上的两个点,并且DE∥BC,AD:BD=3:2,则△ADE与四边形BCED的面积之比为( )
A.3:5 B.4:25
C.9:16 D.9:25
10.如图,若二次函数y=ax2+bx+c(a≠0)的图象的对称轴为直线x=1,与y轴交于点C,与x轴交于点A,点B(﹣1,0),则下列结论:①abc>0;②二次函数的最大值为a+b+c;③a﹣b+c<0;④b2﹣4ac<0;⑤当y>0时,﹣1<x<3;⑥3a+c=0;其中正确的结论有( )
A.3个 B.4个 C.5个 D.6个
二.填空题(共5小题,每小题3分,共15分)
11.分解因式:8x2﹣2y2= .
12.一个正多边形的每个内角为135°,则这个正多边形的边数为 .
13.已知a,b是方程x2+x﹣3=0的两个实数根,则a2﹣b﹣3的值是 .
14.如图,在Rt△ABC中,∠C=90°,以顶点B为圆心,适当长度为半径画弧,分别交AB,BC于点M,N,再分别以点M,N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线BP交AC于点D.若∠A=45°,则 .
15.如图,在边长为6的菱形ABCD中,∠A=60°,M是AD边上的一点,且AMAD,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A'MN,连接A'C,则A'C长度的最小值是 .
三.解答题(一)(本大题共3小题,每小题8分,共24分)
16.计算:.
17.(1)解方程组:;
(2)解不等式:.
18.如图,D、E分别是AB、AC上的点,AD=AE,∠B=∠C,求证:BD=CE.
四.解答题(二)(本大题共3小题,每小题9分,共27分)
19.某校对学生进行了一次系统全面的垃圾分类宣传.为了解这次宣传的效果,从全校学生中随机抽取部分学生进行了一次测试,测试结果共分为四个等级:A.优秀;B.良好;C.及格;D.不及格.根据调查统计结果,绘制了如图所示的不完整的统计表.
(1)本次共调查了 名学生,请补全条形统计图;
(2)在扇形统计图中,m的值是 ,D对应的扇形圆心角的度数是 ;
(3)若该校共有2000名学生,根据抽样调查的结果,请你估计该校不合格的学生人数;
(4)某班要从在这次测试成绩为优秀的小明和小亮中选一人参加知识竞赛.班长设计了如下游戏来确定人选,具体规则是:把四个完全相同的乒乓球分别标上数字1,2,3,4.然后放到一个不透明的袋中充分摇匀,两人同时从袋中各摸出一个球.若摸出的两个球上的数字和为奇数,则小明参加,否则小亮参加.请用树状图或列表法说明这个游戏规则是否公平.
20.如图,在Rt△ABC中,∠ABC=90°,过点B作AC的平行线BD,使得BD=AB,连结AD交BC于点E,过点B作AD的垂线分别交AD,AC于点F,G,连结DG.
(1)求证:四边形ABDG是菱形.
(2)当EF=3,tan∠BGA=2时,求AC的长.
21.某校组织学生到某品牌运动鞋直销店参加社会实践活动,他们参与了该品牌运动鞋的销售工作,已知该运动鞋每双的成本价为130元,为寻求合适的销售价格进行了4天的试销,试销情况如下表所示:
第1天 第2天 第3天 第4天
售价x(元/双) 225 300 375 450
销售量y(双) 40 30 24 20
(1)观察表中数据,x,y满足什么函数关系?请求出这个函数关系式;
(2)在(1)的条件下,若直销店计划每天的销售利润为4500元,则其售价应定为多少元?
五.解答题(三)(本大题共2小题,每小题12分,共24分)
22.如图,在Rt△ABC中,∠ACB=90°,点D是AB的中点,以CD为直径作⊙O,与BC交于点E,过点E作⊙O的切线EF,交AB于点F.
(1)求证:EF⊥AB;
(2)若⊙O的半径是,,求DF的长.
23.如图1,在平面直角坐标系中,一次函数的图象分别交x,y轴于点A、B,抛物线经过点A、B,点P为第四象限内抛物线上的一个动点.
(1)写出点A、点B的坐标;
(2)求此抛物线对应的函数表达式;
(3)如图2,过点P作PM∥y轴,分别交直线AB、x轴于点C、D,若以点P、B、C为顶点的三角形与△ACD相似,求点P的坐标.
2023年广东省中考数学考前热身(三)
参考答案与试题解析
一.选择题(共10小题)
1.【解答】解:﹣5的绝对值等于5,
即|﹣5|=5.
故选:A.
2.【解答】解:32万=320000=3.2×105.
故选:C.
3.【解答】解:∵直线l1∥l2,∠1=52°,
∴∠ABC=∠1=52°,
∵AC⊥l2,
∴∠ACB=90°,
∴∠2=180°﹣∠ABC﹣∠ACB=180°﹣52°﹣90°=38°,
故选:B.
4.【解答】解:A、与不属于同类二次根式,不能运算,故A不符合题意;
B、a÷a﹣2=a3,故B符合题意;
C、,故C不符合题意;
D、,故D不符合题意;
故选:B.
5.【解答】解:点M(﹣4,﹣2)先向上平移3个单位,再向左平移2个单位,得到点N的坐标是(﹣4﹣2,﹣2+3),即(﹣6,1),
故选:A.
6.【解答】解:将7个数据按从小到大的顺序排列为55,55,57,58,60,60,60,
60出现了三次,次数最多,所以这组数据的众数为60,
中间的一个数是58,所以中位数为58.
故选:B.
7.【解答】解:数字为﹣4的面的对面上的数字是﹣3,其积为(﹣4)×(﹣3)=12.
故选:B.
8.【解答】解:∵关于x的一元二次方程kx2﹣2x0有两个不相等的实数根,
∴,
解得:k<2且k≠0,
∴k的值不可能是0.
故选:C.
9.【解答】解:∵AD:BD=3:2,
∴AD:AB=3:5,
∵DE∥BC,
∴△ADE∽△ABC,
∴()2=()2,
∴△ADE与四边形BCED的面积之比是9:16,
故选:C.
10.【解答】解:∵二次函数对称轴在y轴右侧,与y轴交在正半轴,
∴ab<0,c>0,abc<0.
∴故①不正确;
∵二次函数y=ax2+bx+c(a≠0)图象的对称轴为直线x=1,
∴顶点坐标为(1,a+b+c),且开口向下,二次函数的最大值为a+b+c,
故②正确;
∵抛物线过B(﹣1,0),
∴x=﹣1时,y=0,即a﹣b+c=0,
故③不正确;
∵抛物线与x轴有两个交点,
∴b2﹣4ac>0,
故④不正确;
∵对称轴为直线x=1,B(﹣1,0),
∴A(3,0),
由图象可知,﹣1<x<3时,y>0,
故⑤正确;
∵x1,即b=﹣2a,
而x=﹣1时,y=0,即a﹣b+c=0,
∴a+2a+c=0,
∴c+3a=0.
故⑥正确.
故选:A.
二.填空题(共5小题)
11.【解答】解:8x2﹣2y2
=2(4x2﹣y2)
=2(2x+y)(2x﹣y),
故答案为:2(2x+y)(2x﹣y).
12.【解答】解:180°﹣135°=45°,
360÷45=8.
故答案为:八.
13.【解答】解:∵a,b是方程x2+x﹣3=0的两个实数根,
∴a+b=﹣1,
把x=a代入方程得:a2+a﹣3=0,即a2=3﹣a,
则原式=3﹣a﹣b﹣3
=﹣(a+b)
=1.
故答案为:1.
14.【解答】解:由作法得BD平分∠ABC,
过D点作DH⊥AB于H点,如图,
∴DH=DC,
∴,
∵∠C=90°,∠A=45°,
∴△ABC为等腰直角三角形,
∴ABBC,
∴.
故答案为:.
15.【解答】解:如图,过点M作MH⊥CD交CD延长线于点H,连接CM,
∵AMAD,AD=CD=6,
∴AM=2,MD=4,
∵CD∥AB,
∴∠HDM=∠A=60°,
∴HDMD=2,HMHD,
∴CH=8,
∴MC,
∵将△AMN沿MN所在直线翻折得到△A′MN,
∴AM=A'M=2,
∴点A'在以M为圆心,AM为半径的圆上,
∴当点A'在线段MC上时,A'C长度有最小值,
∴A'C长度的最小值=MC﹣MA'2,
故答案为:2.
三.解答题(共8小题)
16.【解答】解:原式=241
3.
17.【解答】解:(1),
①+②,得:5x=5,
解得x=1,
将x=1代入①,得:3+y=4,
解得y=1,
∴方程组的解为;
(2)由7(x﹣5)+2(x+1)>﹣15,得:x>2,
由0,得:x>1,
则不等式组的解集为x>2.
18.【解答】证明:∵AD=AE,∠B=∠C,
又∠A=∠A,
在△ABE与△ACD中,
,
∴△ABE≌△ACD(AAS),
∴AB=AC,
∴AB﹣AD=AC﹣AE,
∴BD=CE.
19.【解答】解:(1)根据题意得:20÷40%=50(名),50﹣(20+15+10)=5(名),
补全条形统计图,如图所示:
故答案为:50;
(2)根据题意得:15÷50×100%=30%,即m=30,10÷50×360°=72°,
则在扇形统计图中,m的值是30,D对应的扇形圆心角的度数是72°;
故答案为:30,72°;
(3)根据题意得:2000400(名),
则估计该校不合格的学生人数约为400名;
(4)根据题意,列表如下:
1 2 3 4
1 ﹣﹣﹣﹣﹣﹣﹣﹣﹣ (1,2) (1,3) (1,4)
2 (2,1) ﹣﹣﹣﹣﹣﹣﹣﹣﹣ (2,3) (2,4)
3 (3,1) (3,2) ﹣﹣﹣﹣﹣﹣﹣﹣﹣ (3,4)
4 (4,1) (4,2) (4,3) ﹣﹣﹣﹣﹣﹣﹣﹣﹣
所有等可能的情况数有12种,其中和为奇数的有(1,2),(1,4),(2,1),(2,3),(3,2),(3,4),(4,1),(4,3),共8种,
∴P(小明参加),P(小亮参加)=1,
∵,
∴这个游戏规则不公平.
20.【解答】(1)证明:∵AB=BD,
∴△ABD是等腰三角形,
∵BG⊥AD,
∴AF=FD,
在△AFG与△DFG中,
,
∴△AFG≌△DFG(SAS),
∴AG=GD,∠AGF=∠DGF,
∵BD∥AC,
∴∠DBF=∠AGF,
∴∠DGF=∠DBF,
∴BD=DG,
∴AB=BD=DG=AG,
∴四边形ABDG是菱形;
(2)解:∵∠ABC=90°,
∴∠CBF+∠ABF=90°,
∵四边形ABDG是菱形,
∴∠ABF=∠BGA=∠DBG,
∵tan∠BGA=2,
∴tan∠ABF,
∴AF=2BF,
设BF=x,则AF=2x=DF,
∴ABx=BD,
∴AE=AF+EF=2x+3,
在Rt△BEF中,根据勾股定理得:BE2=BF2+EF2=x2+9,
在RtABE中,AB2+BE2=AE2,
∴(x)2+x2+9=(2x+3)2,
解得x=6或x=0(舍去),
∴BF=6,
∴AF=12,
∴AB=BD=6,AE=AF+EF=15,
∴DE=DF﹣EF=12﹣3=9,
∵BD∥AC,
∴△DBE∽△CAE,
∴,
∴,
∴AC=10.
∴AC的长为10.
21.【解答】解:(1)由表中的数据可得:xy=9000,
∴,
∴y是x的反比例函数,
所以这个函数关系式为;
(2)根据题意得:(x﹣130)y=4500,
将代入得,,
解得:x=260,
经检验,x=260是原方程的解且适合题意.
答:售价应定为260元.
22.【解答】(1)证明:连接OE,
∵∠ACB=90°,AD=DB,
∴DC=DB=DA,
∵CD是直径,
∴∠CFD=90°,即DE⊥BC,
∴CE=EB,
∵OC=OD,CE=BE,
∴OE是△CDB的中位线,
∴OE∥BD,
∴∠OEC=∠B,
∵EF是⊙O的切线,
∴∠OEF=90°,
∴∠OEC+∠BEF=90°,
∴∠BEF+∠B=90°,
∴∠EFB=90°,
∴EF⊥AB;
(2)解:连接DE,
在Rt△ABC中,
∵点D是AB的中点,CD=5,
∴AD=BD=5,
∴AB=10,
∵cos∠ACD,
∴AC=106,
∴BC8,
∵CD是⊙O的直径,
∴∠CED=90°,
∴BE=CEBC=4,
∴DE3,
∴S△BDEDE BEBD EF,
∴EF.
∴DF.
23.【解答】解:(1)令x=0,得2,则B(0,﹣2),
令0,解得x=4,则A(4,0),
(2)把A(4,0),B(0,﹣2)代入y=x2+bx+c(a≠0)中,
得,
解得.
∴抛物线的解析式为:y=x2x﹣2;
(3)∵PM∥y轴,
∴∠ADC=90°.
∵∠ACD=∠BCP,
∴以点P、B、C为顶点的三角形与以点A、C、D为顶点的三角形相似,存在两种情况:
①当∠CBP=90°时,如图,过P作PN⊥y轴于N,
∵∠ABO+∠PBN=∠ABO+∠OAB=90°,
∴∠PBN=∠OAB,
∵∠AOB=∠BNP=90°,
∴Rt△PBN∽Rt△BAO.
∴.
设P的坐标为(x,x2x﹣2).
∴,化简得.
解得x=0(舍去)或x.
∴P(,﹣5);
②当∠CPB=90°时,如图2,则PB∥x轴,所以B和P是对称点.
所以当y=﹣2时,则x2x﹣2=﹣2,解得x=0(舍去)或x.
∴P(,﹣2).
综上,点P的坐标(,﹣5)或(,﹣2).
同课章节目录
