圆心角,弧,弦和弦心距的关系[下学期]
图片预览

文档简介
16.2圆心角、弧、弦与弦心距的关系
知识技能目标
1.理解弦及弦心距的概念和特征;
2.通过实践操作,理解并掌握同圆中圆心角、弧、弦和弦心距的关系;
3.利用同圆中圆心角、弧、弦和弦心距的关系解答有关几何问题.
情感态度目标
1. 通过圆的对称性研究同圆中圆心角、弧、弦和弦心距的关系,感受分类讨论及由特殊到一般研究几何图形性质的思想方法;
2.创设具体生动的教学情境,体验数学是充满探索性和创造性的.
重点和难点
重点:同圆中圆心角、弧、弦和弦心距的关系特征;
难点:同圆中,四组量中只要一组量相等,其余三组量也相等
教学过程
一、导入新课:
1、圆是一个旋转图形:
圆可以看成是一个点绕着圆心旋转360度后所形成的曲线
2、圆的性质:同圆的半径相等
二、新课讲解:
1、认识圆心角、弧、弦和弦心距的概念
(1)半径:圆心到圆上任意一点之间的线段
直径:通过圆心且两个端点在圆上的线段
弦:连结圆上任意两点的线段
* 直径是圆中最长的弦
(2)弧:圆上任意两点之间的部分
半圆:圆上任意一条直径的两个端点分成的两条弧
优弧:大于半圆的弧,用三个大写字母表示
劣弧:小于半圆的弧,用两个大写字母表示
(3)圆心角:顶点在圆心的角
圆周角:顶点在圆周上的角
* 同圆中,同弧所对圆心角的度数是圆周角度数的2倍
* 直径所对的圆周角的度数是90度
(4)弦心距:圆心到弦的距离
所对的弦是________________
∠AOD所对的弧是________________
所对的圆心角是________________
OE是弦__________所对的____________。
弦CD所对的弧是____________________。
练习:
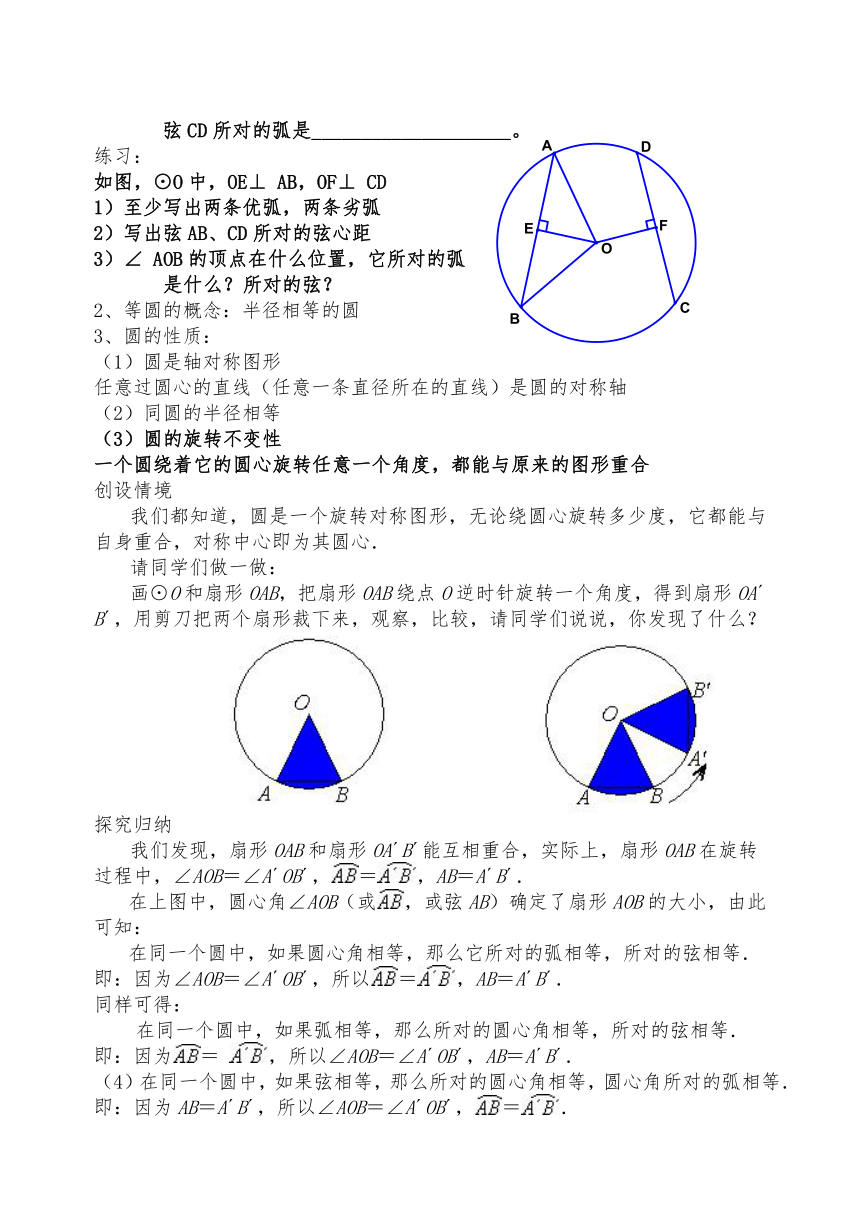
如图,⊙O中,OE⊥ AB,OF⊥ CD
1)至少写出两条优弧,两条劣弧
2)写出弦AB、CD所对的弦心距
3)∠ AOB的顶点在什么位置,它所对的弧
是什么?所对的弦?
2、等圆的概念:半径相等的圆
3、圆的性质:
(1)圆是轴对称图形
任意过圆心的直线(任意一条直径所在的直线)是圆的对称轴
(2)同圆的半径相等
(3)圆的旋转不变性
一个圆绕着它的圆心旋转任意一个角度,都能与原来的图形重合
创设情境
我们都知道,圆是一个旋转对称图形,无论绕圆心旋转多少度,它都能与自身重合,对称中心即为其圆心.
请同学们做一做:
画⊙O和扇形OAB,把扇形OAB绕点O逆时针旋转一个角度,得到扇形OA B ,用剪刀把两个扇形裁下来,观察,比较,请同学们说说,你发现了什么?
探究归纳
我们发现,扇形OAB和扇形OA B 能互相重合,实际上,扇形OAB在旋转过程中,∠AOB=∠A OB ,=,AB=A B .
在上图中,圆心角∠AOB(或,或弦AB)确定了扇形AOB的大小,由此可知:
在同一个圆中,如果圆心角相等,那么它所对的弧相等,所对的弦相等.
即:因为∠AOB=∠A OB ,所以=,AB=A B .
同样可得:
在同一个圆中,如果弧相等,那么所对的圆心角相等,所对的弦相等.
即:因为= ,所以∠AOB=∠A OB ,AB=A B .
(4)在同一个圆中,如果弦相等,那么所对的圆心角相等,圆心角所对的弧相等.
即:因为AB=A B ,所以∠AOB=∠A OB ,=.
上述圆心角、弧、弦三者的关系也可这样叙述:
在同一个圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量也分别相等.
例1、已知:在⊙O中,AB=CD,OE、
OF分别是AB、AC的弦心距
求证:1)
2)OE=OF
例2、已知:⊙O中,
求证:∠B=∠C
例3、已知:⊙O中,
OE、OF分别是弦AB、CD的弦心距
求证:1)AB=CD
2)OE=OF
例4、已知:在⊙O中,AB是直径,弦BC、BD的弦心距分别是OE、OF,弦AC、AD的弦心距分别为OG、OH
1)若OE=OF,求证 :
2)若OE=OF,求证:OG=OH
3)若∠1=∠2,求证∠3=∠4
例5、如图,是圆O的三条劣弧,如果
那么弦AB+CD与弦EF的关系是什么?
思维训练:
下面的说法正确吗 为什么
如图,因为
根据圆心角、弧、弦、弦心距的关系定理可知
解:不正确,没有强调在同圆或等圆中,如同心圆中,同一个圆心角所对的弧不相等。
小结:
利用圆的旋转不变性得到圆的一个重要性质:
在同圆或等圆中,如果两个圆心角、两条劣弧
(或优弧)两条弦或两条弦的弦心距这四组量中
存在一组量相等,那么它们所对应的其余三组也相等
作业:A册 P48~ P49 1~ 4
一课一练
同步 P105~ P107 1~ 7
思考:
已知:AB为⊙O的直径,C为圆周上一点,过圆心O作OD//AC,交⊙O于点D,
求证:
B
4
3
1
2
C
D
B
O
A
知识技能目标
1.理解弦及弦心距的概念和特征;
2.通过实践操作,理解并掌握同圆中圆心角、弧、弦和弦心距的关系;
3.利用同圆中圆心角、弧、弦和弦心距的关系解答有关几何问题.
情感态度目标
1. 通过圆的对称性研究同圆中圆心角、弧、弦和弦心距的关系,感受分类讨论及由特殊到一般研究几何图形性质的思想方法;
2.创设具体生动的教学情境,体验数学是充满探索性和创造性的.
重点和难点
重点:同圆中圆心角、弧、弦和弦心距的关系特征;
难点:同圆中,四组量中只要一组量相等,其余三组量也相等
教学过程
一、导入新课:
1、圆是一个旋转图形:
圆可以看成是一个点绕着圆心旋转360度后所形成的曲线
2、圆的性质:同圆的半径相等
二、新课讲解:
1、认识圆心角、弧、弦和弦心距的概念
(1)半径:圆心到圆上任意一点之间的线段
直径:通过圆心且两个端点在圆上的线段
弦:连结圆上任意两点的线段
* 直径是圆中最长的弦
(2)弧:圆上任意两点之间的部分
半圆:圆上任意一条直径的两个端点分成的两条弧
优弧:大于半圆的弧,用三个大写字母表示
劣弧:小于半圆的弧,用两个大写字母表示
(3)圆心角:顶点在圆心的角
圆周角:顶点在圆周上的角
* 同圆中,同弧所对圆心角的度数是圆周角度数的2倍
* 直径所对的圆周角的度数是90度
(4)弦心距:圆心到弦的距离
所对的弦是________________
∠AOD所对的弧是________________
所对的圆心角是________________
OE是弦__________所对的____________。
弦CD所对的弧是____________________。
练习:
如图,⊙O中,OE⊥ AB,OF⊥ CD
1)至少写出两条优弧,两条劣弧
2)写出弦AB、CD所对的弦心距
3)∠ AOB的顶点在什么位置,它所对的弧
是什么?所对的弦?
2、等圆的概念:半径相等的圆
3、圆的性质:
(1)圆是轴对称图形
任意过圆心的直线(任意一条直径所在的直线)是圆的对称轴
(2)同圆的半径相等
(3)圆的旋转不变性
一个圆绕着它的圆心旋转任意一个角度,都能与原来的图形重合
创设情境
我们都知道,圆是一个旋转对称图形,无论绕圆心旋转多少度,它都能与自身重合,对称中心即为其圆心.
请同学们做一做:
画⊙O和扇形OAB,把扇形OAB绕点O逆时针旋转一个角度,得到扇形OA B ,用剪刀把两个扇形裁下来,观察,比较,请同学们说说,你发现了什么?
探究归纳
我们发现,扇形OAB和扇形OA B 能互相重合,实际上,扇形OAB在旋转过程中,∠AOB=∠A OB ,=,AB=A B .
在上图中,圆心角∠AOB(或,或弦AB)确定了扇形AOB的大小,由此可知:
在同一个圆中,如果圆心角相等,那么它所对的弧相等,所对的弦相等.
即:因为∠AOB=∠A OB ,所以=,AB=A B .
同样可得:
在同一个圆中,如果弧相等,那么所对的圆心角相等,所对的弦相等.
即:因为= ,所以∠AOB=∠A OB ,AB=A B .
(4)在同一个圆中,如果弦相等,那么所对的圆心角相等,圆心角所对的弧相等.
即:因为AB=A B ,所以∠AOB=∠A OB ,=.
上述圆心角、弧、弦三者的关系也可这样叙述:
在同一个圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量也分别相等.
例1、已知:在⊙O中,AB=CD,OE、
OF分别是AB、AC的弦心距
求证:1)
2)OE=OF
例2、已知:⊙O中,
求证:∠B=∠C
例3、已知:⊙O中,
OE、OF分别是弦AB、CD的弦心距
求证:1)AB=CD
2)OE=OF
例4、已知:在⊙O中,AB是直径,弦BC、BD的弦心距分别是OE、OF,弦AC、AD的弦心距分别为OG、OH
1)若OE=OF,求证 :
2)若OE=OF,求证:OG=OH
3)若∠1=∠2,求证∠3=∠4
例5、如图,是圆O的三条劣弧,如果
那么弦AB+CD与弦EF的关系是什么?
思维训练:
下面的说法正确吗 为什么
如图,因为
根据圆心角、弧、弦、弦心距的关系定理可知
解:不正确,没有强调在同圆或等圆中,如同心圆中,同一个圆心角所对的弧不相等。
小结:
利用圆的旋转不变性得到圆的一个重要性质:
在同圆或等圆中,如果两个圆心角、两条劣弧
(或优弧)两条弦或两条弦的弦心距这四组量中
存在一组量相等,那么它们所对应的其余三组也相等
作业:A册 P48~ P49 1~ 4
一课一练
同步 P105~ P107 1~ 7
思考:
已知:AB为⊙O的直径,C为圆周上一点,过圆心O作OD//AC,交⊙O于点D,
求证:
B
4
3
1
2
C
D
B
O
A
