人教版七年级下册8.2.1代入消元法解二元一次方程组 说课课件(共25张PPT)
文档属性
| 名称 | 人教版七年级下册8.2.1代入消元法解二元一次方程组 说课课件(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-13 15:34:11 | ||
图片预览






文档简介
(共25张PPT)
人教版义务教育课程标准实验教科书
七年级下册
代入消元法
教学背景分析
教学目标
教学重点、难点
教法与学法
教学背景分析
教学过程
本节内容的地位与作用
本节主要内容是在上节已认识二元一次方程(组)和二元一次方程(组)的解等概念的基础上,来学习解方程组的第一种方法——代入消元法。并初步体会“将未知数的个数由多化少、逐一解决”的消元思想。它既是对解一元一次方程的延伸与拓展,又是为以后学习求一次函数和二次函数的解析奠定了基础,具有非常重要的作用。
已有知识:
(1)、在《整式加减》一章的化简求值问题中对
“代入”一词的意义与方法已有了一定的理解;
(2)、在前几章几何推理学习中,“等量代换”的
意义已被学生所接纳;
(3)、会解较简单的含字母系数的一元一次方程。
存在困难:
确定代入消元的切入点。
学生已有知识与存在困难
代入消元法
教学背景分析
教学目标
教学重点、难点
教法与学法
教学目标
教学过程
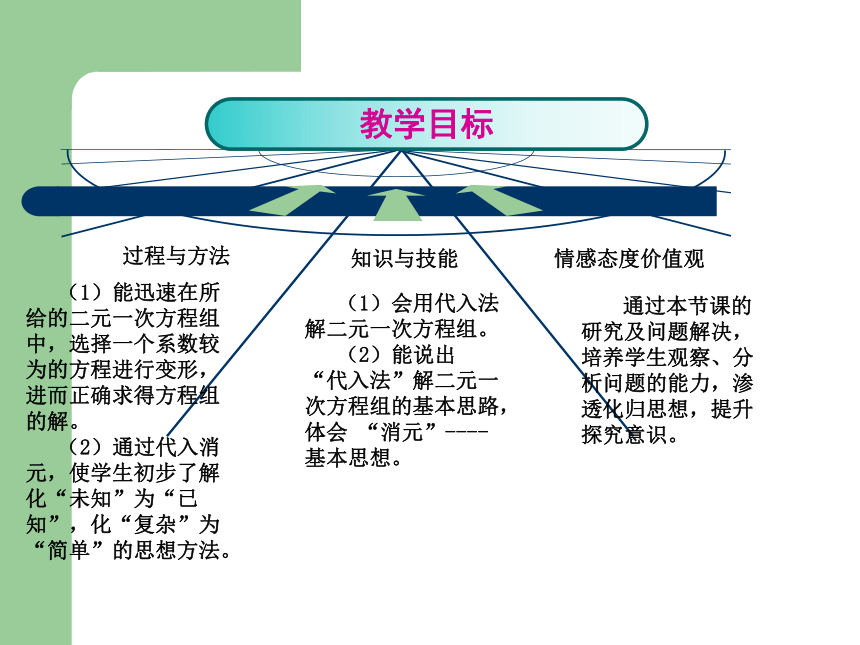
知识与技能
(1)会用代入法解二元一次方程组。
(2)能说出 “代入法”解二元一次方程组的基本思路,体会 “消元”----基本思想。
过程与方法
(1)能迅速在所给的二元一次方程组中,选择一个系数较为的方程进行变形,进而正确求得方程组的解。
(2)通过代入消元,使学生初步了解化“未知”为“已知”,化“复杂”为“简单”的思想方法。
情感态度价值观
通过本节课的研究及问题解决,培养学生观察、分析问题的能力,渗透化归思想,提升探究意识。
教学目标
代入消元法
教材分析
教学目标
教学重点、难点
教法与学法
教学重点、难点
教学过程
重点
会用代入消元法解二元一次方程组。
难点
探索如何用代入法将二元转化为一元的消元过程。
教学重点、难点
代入消元法
教材分析
教学目标
教学重点、难点
教法与学法
教法与学法
教学过程
教法与学法
(一)教法
学生已经有解一元一次方程的经验,解二元一次方程组的关键就是消元,“化二元为一元”,故本节课的教学始终抓住消元的思想方法。针对本节特点,在教学过程中我采用引导发现的教学方式,通过简单实际问题方程组的求解,逐层推进的问题链的设计,突破教学难点,实现新知的教学。
教法与学法
(二)学法
本节课教学,坚持让学生从“问题引入—探究解法—归纳总结—能力提升”的过程来获得新知。学生在对比分析中,由“等量代换”为出发点发现“代入消元”的方法,进而归纳小结得方程解法,体会消元思想。
代入消元法
教材分析
教学目标
教学重点、难点
教法与学法
教学过程
教学过程
引入
新课
课堂
检测
布置
作业
课堂
小结
应用
新知
探究
新知
教学过程
已知如图,长方形长与宽的和为18。
(1)若长是10,则长、宽各是多少?
解:设游泳池的宽为x米,
长为y米,则
x
y
问题情境
如何求解?
x
10
+
=
18
x + y = 18
y =10
{
①
②
已知如图,长方形长与宽的和为18。
(2)若长是宽的2倍,则长、宽各是多少?
解:设游泳池的宽为x米,
长为y米,则
x
y
问题情境
想一想,如何求解?
x
2x
+
=
18
x + y = 18
y =2x
{
①
②
分析
例1 解方程组
2y – 3x = 1
x = y - 1
解:
①
②
把②代入①得:
2y – 3(y – 1)= 1
2y – 3y + 3 = 1
2y – 3y = 1 - 3
- y = - 2
y = 2
把y = 2代入②,得
x = y – 1 = 2 – 1 = 1
∴方程组的解是
x = 1
y = 2
2 y – 3 x = 1
x = y - 1
(y-1)
谈谈思路
例1 解方程组
2y – 3x = 1
x = y - 1
解:
①
②
把②代入①得:
2y – 3(y – 1)= 1
2y – 3y + 3 = 1
2y – 3y = 1 - 3
- y = - 2
y = 2
把y = 2代入②,得
x = y – 1 = 2 – 1 = 1
∴方程组的解是
x = 1
y = 2
谈谈思路
变:
2y – 3x = 1
x – y = – 1
①
②
例2 解方程组
解:
①
②
由①得:
x = 3+ y
③
把③代入②得:
3(3+y)– 8y= 14
把y= – 1代入③,得
x = 2
1、将方程组里的一个方程变形,用含有一个未知数的式子表示另一个未知数;
2、用这个式子代替另一个方程中相应的未知数,得到一个一元一次方程,求得一个未知数的值;
3、把这个未知数的值代入上面的式子,求得另一个未知数的值;
4、写出方程组的解。
用代入法解二元一次方程组的一般步骤
变
代
求
写
x –y = 3
3x -8 y = 14
9+3y– 8y= 14
– 5y= 5
y= – 1
∴方程组的解是
x =2
y = -1
说说方法
归 纳:
代入消元法解方程组的基本思想是:消元。
将方程组的一个方程中的某个未知数用含有另一个未知数的代数式表示,并代入另一个方程,从而消去一个未知数,把解二元一次方程组转化为解一元一次方程。这种解方程组的方法称为代入消元法,简称为代入法。
1、将方程组里的一个方程变形,用含有一个未知数的一次式表示另一个未知数
2、用这个一次式代替另一个方程中相应的未知数,得到一个一元一次方程,求得一个未知数的值
3、把这个未知数的值代入一次式,求得另一个未知数的值
4、写出方程组的解
用代入法解二元一次方程组的一般步骤
1、 解方程组
2x - 4y = 5
x = 3y - 1
①
3x – 6z = 4
x + 5z = 6
②
讨论
4x + 5y = 4
用含x 的一次式表示y:
用含y 的一次式表示x:
x =
y =
学以致用
2、用代入法解二元一次方程组
(1)
(2)
知识拓展
2.代入法的基本思想:消元。
3.代入法解二元一次方程组主要步骤:
一变,二代,三求,四写
1.代入消元法
课堂小结
布置作业
1、若方程5x 2m+n+4y 3m-2n = 9是关于x、y的二元一次方程,求m 、n 的值.
2、如果∣y + 3x - 2∣+∣5x + 2y -2∣= 0,求 x 、y 的值.
选做题
基础题
学案 1、2
解二元一次方程组
(1)
(2)
(3)
课堂小测
人教版义务教育课程标准实验教科书
七年级下册
代入消元法
教学背景分析
教学目标
教学重点、难点
教法与学法
教学背景分析
教学过程
本节内容的地位与作用
本节主要内容是在上节已认识二元一次方程(组)和二元一次方程(组)的解等概念的基础上,来学习解方程组的第一种方法——代入消元法。并初步体会“将未知数的个数由多化少、逐一解决”的消元思想。它既是对解一元一次方程的延伸与拓展,又是为以后学习求一次函数和二次函数的解析奠定了基础,具有非常重要的作用。
已有知识:
(1)、在《整式加减》一章的化简求值问题中对
“代入”一词的意义与方法已有了一定的理解;
(2)、在前几章几何推理学习中,“等量代换”的
意义已被学生所接纳;
(3)、会解较简单的含字母系数的一元一次方程。
存在困难:
确定代入消元的切入点。
学生已有知识与存在困难
代入消元法
教学背景分析
教学目标
教学重点、难点
教法与学法
教学目标
教学过程
知识与技能
(1)会用代入法解二元一次方程组。
(2)能说出 “代入法”解二元一次方程组的基本思路,体会 “消元”----基本思想。
过程与方法
(1)能迅速在所给的二元一次方程组中,选择一个系数较为的方程进行变形,进而正确求得方程组的解。
(2)通过代入消元,使学生初步了解化“未知”为“已知”,化“复杂”为“简单”的思想方法。
情感态度价值观
通过本节课的研究及问题解决,培养学生观察、分析问题的能力,渗透化归思想,提升探究意识。
教学目标
代入消元法
教材分析
教学目标
教学重点、难点
教法与学法
教学重点、难点
教学过程
重点
会用代入消元法解二元一次方程组。
难点
探索如何用代入法将二元转化为一元的消元过程。
教学重点、难点
代入消元法
教材分析
教学目标
教学重点、难点
教法与学法
教法与学法
教学过程
教法与学法
(一)教法
学生已经有解一元一次方程的经验,解二元一次方程组的关键就是消元,“化二元为一元”,故本节课的教学始终抓住消元的思想方法。针对本节特点,在教学过程中我采用引导发现的教学方式,通过简单实际问题方程组的求解,逐层推进的问题链的设计,突破教学难点,实现新知的教学。
教法与学法
(二)学法
本节课教学,坚持让学生从“问题引入—探究解法—归纳总结—能力提升”的过程来获得新知。学生在对比分析中,由“等量代换”为出发点发现“代入消元”的方法,进而归纳小结得方程解法,体会消元思想。
代入消元法
教材分析
教学目标
教学重点、难点
教法与学法
教学过程
教学过程
引入
新课
课堂
检测
布置
作业
课堂
小结
应用
新知
探究
新知
教学过程
已知如图,长方形长与宽的和为18。
(1)若长是10,则长、宽各是多少?
解:设游泳池的宽为x米,
长为y米,则
x
y
问题情境
如何求解?
x
10
+
=
18
x + y = 18
y =10
{
①
②
已知如图,长方形长与宽的和为18。
(2)若长是宽的2倍,则长、宽各是多少?
解:设游泳池的宽为x米,
长为y米,则
x
y
问题情境
想一想,如何求解?
x
2x
+
=
18
x + y = 18
y =2x
{
①
②
分析
例1 解方程组
2y – 3x = 1
x = y - 1
解:
①
②
把②代入①得:
2y – 3(y – 1)= 1
2y – 3y + 3 = 1
2y – 3y = 1 - 3
- y = - 2
y = 2
把y = 2代入②,得
x = y – 1 = 2 – 1 = 1
∴方程组的解是
x = 1
y = 2
2 y – 3 x = 1
x = y - 1
(y-1)
谈谈思路
例1 解方程组
2y – 3x = 1
x = y - 1
解:
①
②
把②代入①得:
2y – 3(y – 1)= 1
2y – 3y + 3 = 1
2y – 3y = 1 - 3
- y = - 2
y = 2
把y = 2代入②,得
x = y – 1 = 2 – 1 = 1
∴方程组的解是
x = 1
y = 2
谈谈思路
变:
2y – 3x = 1
x – y = – 1
①
②
例2 解方程组
解:
①
②
由①得:
x = 3+ y
③
把③代入②得:
3(3+y)– 8y= 14
把y= – 1代入③,得
x = 2
1、将方程组里的一个方程变形,用含有一个未知数的式子表示另一个未知数;
2、用这个式子代替另一个方程中相应的未知数,得到一个一元一次方程,求得一个未知数的值;
3、把这个未知数的值代入上面的式子,求得另一个未知数的值;
4、写出方程组的解。
用代入法解二元一次方程组的一般步骤
变
代
求
写
x –y = 3
3x -8 y = 14
9+3y– 8y= 14
– 5y= 5
y= – 1
∴方程组的解是
x =2
y = -1
说说方法
归 纳:
代入消元法解方程组的基本思想是:消元。
将方程组的一个方程中的某个未知数用含有另一个未知数的代数式表示,并代入另一个方程,从而消去一个未知数,把解二元一次方程组转化为解一元一次方程。这种解方程组的方法称为代入消元法,简称为代入法。
1、将方程组里的一个方程变形,用含有一个未知数的一次式表示另一个未知数
2、用这个一次式代替另一个方程中相应的未知数,得到一个一元一次方程,求得一个未知数的值
3、把这个未知数的值代入一次式,求得另一个未知数的值
4、写出方程组的解
用代入法解二元一次方程组的一般步骤
1、 解方程组
2x - 4y = 5
x = 3y - 1
①
3x – 6z = 4
x + 5z = 6
②
讨论
4x + 5y = 4
用含x 的一次式表示y:
用含y 的一次式表示x:
x =
y =
学以致用
2、用代入法解二元一次方程组
(1)
(2)
知识拓展
2.代入法的基本思想:消元。
3.代入法解二元一次方程组主要步骤:
一变,二代,三求,四写
1.代入消元法
课堂小结
布置作业
1、若方程5x 2m+n+4y 3m-2n = 9是关于x、y的二元一次方程,求m 、n 的值.
2、如果∣y + 3x - 2∣+∣5x + 2y -2∣= 0,求 x 、y 的值.
选做题
基础题
学案 1、2
解二元一次方程组
(1)
(2)
(3)
课堂小测
