菱形的性质[下学期]
图片预览






文档简介
课件17张PPT。 菱 形
(性 质) (一)复习提问
1、什么叫做平行四边形?什么叫矩形?
2、平行四边形和矩形之间的关系是什么? 矩形矩形的定义:有一个角是直角的平行四边形。矩形的性质矩形的判定具有平行四边形的一切特征四个角都是直角对角线相等的平行四边形对角线相等且平分有一个角是直角的平行四边形有三个角是直角的四边形对角线相等且平分的四边形判断下列说法是否正确? ⑴对角线相等的四边形是矩形; ( ) ⑵对角线互相平分且相等的四边形是矩形( ) ⑶有一个角是直角的四边形是矩形; ( ) ⑷有三个角是直角的四边形是矩形; ( ) ⑸四个角都相等的四边形是矩形; ( )
⑹对角线相等,且有一个角是直角的四边形
是矩形; ( ) ⑺对角线互相平分,且有一个角是直角的四边形
是矩形; ( )1、矩形的四个内角都是______。
2、矩形的对角线______且 __________。直角相等互相平分3、在直角三角形中,______角所对的直角边等于斜边的_______。
4、在直角三角形中,斜边上的______等于斜边的______。30度一半中线一半5、平行四边形的一个内角的平分线把较长的边分成5cm、3cm。求平行四边形的周长?
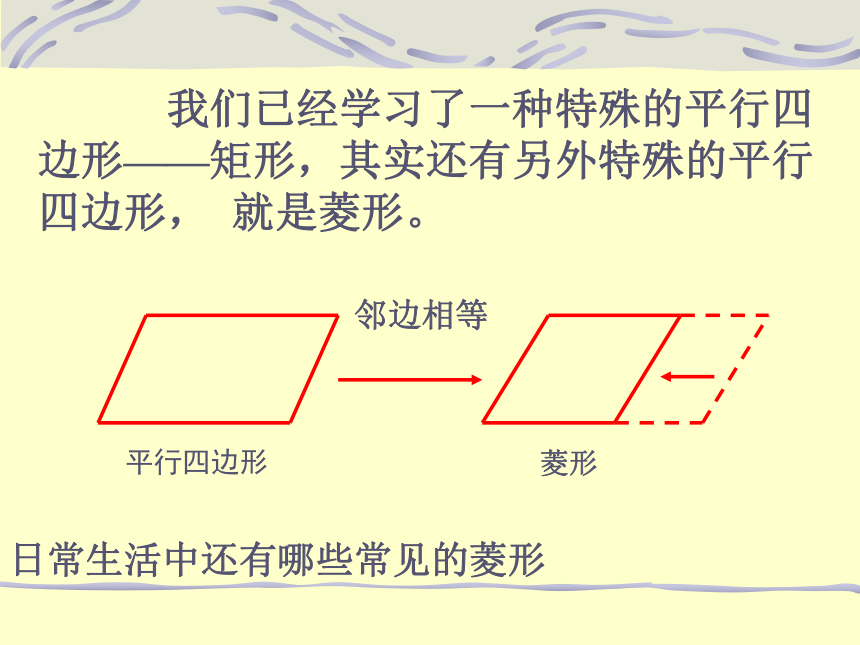
我们已经学习了一种特殊的平行四边形——矩形,其实还有另外特殊的平行四边形, 就是菱形。 邻边相等菱形
日常生活中还有哪些常见的菱形1.菱形定义:
有一组邻边相等的平行四边形叫做菱形. (1)菱形是平行四边形.
(2) 一组邻边相等 2.菱形的性质: 因为菱形是平行四边形,所以它有平行四边形的一切性质,它又是特殊的平行四边形,因此,它又具有特殊的性质 菱形性质定理 1:菱形的四条边都相等. 动手做一做:
将一个矩形的纸对折两次,
剪下一个角,得到一个菱形,观察得到的菱形,
它是轴对称图形吗?有几条对称轴?
对称轴之间有什么位置关系?(书107)探索菱形性质定理2:菱形的对角线互相垂直
并且每一条对角线平分一组对角.你能证明这个性质吗?
已知:菱形ABCD的对角线AC和BD相交于点O,如下图,
求证:AC⊥BD; A D
AC平分∠BAD和∠BCD;
BD平分∠ABC和∠ADC O
B C证明:∵四边形ABCD是菱形
∴AB=AD(菱形的四条边都相等)
在等腰△ABD中
∵BO=DO
∴AC⊥BD,AC平分∠BAD
同理: AC平分∠BCD;
BD平分∠ABC和∠ADC
3.观察对角线把菱形分成的四个三角形,
与一般的平行四边形和矩形进行比较 5、菱形的面积
4、菱形具备有轴对称图形性质,对称轴是两条互相垂直的对角线所在的直线
菱形的面积等于两条对角线长的乘积的一半
即:如果菱形的两条对角线长跟别为a、b;
则菱形的面积:S=1/2 ab
ab 例.已知菱形ABCD的边长为2cm,∠BAD=120°,对角线AC,BD相交于点O,如图,求这个菱形的对角线长和面积
A D
O
B C
练习1 已知菱形ABCD中,E是AB的中点,且DE⊥AB,AB=a.
求:⑴∠ABC的度数 ⑵对角线AC的长⑶菱形ABCD的面积练习2:
1:(口答)矩形,菱形各具有哪些性质?2求证:菱形对角线交点到各边距离相等.方法1:利用全等三角形来证方法2:利用面积来证方法3:利用角平分线的性质来证3.已知菱形的对角线长分别为6cm和 8cm,求菱形的周长和面积. 1、菱形、平行四边形、四边形
的从属关系:
2、菱形性质:
①具有平行四边形的所有性质.
②特有性质:四条边相等;
对角线互相垂直,
且平分每一组对角. 这节课你学到了什么?课堂小结:已知:如图AD是△ABC的角平分线,
DE∥AC交于E,DF∥AB交AC于F.
求证:四边形AEDF是菱形.
A
E
F
B D C
(性 质) (一)复习提问
1、什么叫做平行四边形?什么叫矩形?
2、平行四边形和矩形之间的关系是什么? 矩形矩形的定义:有一个角是直角的平行四边形。矩形的性质矩形的判定具有平行四边形的一切特征四个角都是直角对角线相等的平行四边形对角线相等且平分有一个角是直角的平行四边形有三个角是直角的四边形对角线相等且平分的四边形判断下列说法是否正确? ⑴对角线相等的四边形是矩形; ( ) ⑵对角线互相平分且相等的四边形是矩形( ) ⑶有一个角是直角的四边形是矩形; ( ) ⑷有三个角是直角的四边形是矩形; ( ) ⑸四个角都相等的四边形是矩形; ( )
⑹对角线相等,且有一个角是直角的四边形
是矩形; ( ) ⑺对角线互相平分,且有一个角是直角的四边形
是矩形; ( )1、矩形的四个内角都是______。
2、矩形的对角线______且 __________。直角相等互相平分3、在直角三角形中,______角所对的直角边等于斜边的_______。
4、在直角三角形中,斜边上的______等于斜边的______。30度一半中线一半5、平行四边形的一个内角的平分线把较长的边分成5cm、3cm。求平行四边形的周长?
我们已经学习了一种特殊的平行四边形——矩形,其实还有另外特殊的平行四边形, 就是菱形。 邻边相等菱形
日常生活中还有哪些常见的菱形1.菱形定义:
有一组邻边相等的平行四边形叫做菱形. (1)菱形是平行四边形.
(2) 一组邻边相等 2.菱形的性质: 因为菱形是平行四边形,所以它有平行四边形的一切性质,它又是特殊的平行四边形,因此,它又具有特殊的性质 菱形性质定理 1:菱形的四条边都相等. 动手做一做:
将一个矩形的纸对折两次,
剪下一个角,得到一个菱形,观察得到的菱形,
它是轴对称图形吗?有几条对称轴?
对称轴之间有什么位置关系?(书107)探索菱形性质定理2:菱形的对角线互相垂直
并且每一条对角线平分一组对角.你能证明这个性质吗?
已知:菱形ABCD的对角线AC和BD相交于点O,如下图,
求证:AC⊥BD; A D
AC平分∠BAD和∠BCD;
BD平分∠ABC和∠ADC O
B C证明:∵四边形ABCD是菱形
∴AB=AD(菱形的四条边都相等)
在等腰△ABD中
∵BO=DO
∴AC⊥BD,AC平分∠BAD
同理: AC平分∠BCD;
BD平分∠ABC和∠ADC
3.观察对角线把菱形分成的四个三角形,
与一般的平行四边形和矩形进行比较 5、菱形的面积
4、菱形具备有轴对称图形性质,对称轴是两条互相垂直的对角线所在的直线
菱形的面积等于两条对角线长的乘积的一半
即:如果菱形的两条对角线长跟别为a、b;
则菱形的面积:S=1/2 ab
ab 例.已知菱形ABCD的边长为2cm,∠BAD=120°,对角线AC,BD相交于点O,如图,求这个菱形的对角线长和面积
A D
O
B C
练习1 已知菱形ABCD中,E是AB的中点,且DE⊥AB,AB=a.
求:⑴∠ABC的度数 ⑵对角线AC的长⑶菱形ABCD的面积练习2:
1:(口答)矩形,菱形各具有哪些性质?2求证:菱形对角线交点到各边距离相等.方法1:利用全等三角形来证方法2:利用面积来证方法3:利用角平分线的性质来证3.已知菱形的对角线长分别为6cm和 8cm,求菱形的周长和面积. 1、菱形、平行四边形、四边形
的从属关系:
2、菱形性质:
①具有平行四边形的所有性质.
②特有性质:四条边相等;
对角线互相垂直,
且平分每一组对角. 这节课你学到了什么?课堂小结:已知:如图AD是△ABC的角平分线,
DE∥AC交于E,DF∥AB交AC于F.
求证:四边形AEDF是菱形.
A
E
F
B D C
