山东省聊城市第四中学2022-2023学年高一下学期5月月考数学试题(含答案)
文档属性
| 名称 | 山东省聊城市第四中学2022-2023学年高一下学期5月月考数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 894.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-11 22:42:52 | ||
图片预览



文档简介
聊城市第四中学2022-2023学年高一下学期5月月考
数学试题
本试卷分选择题和非选择题两部分.满分150分.考试用时120分钟
一 单项选择题:本大题共8小题,每小题5分,共40分,在每小题给出四个选项中,只有一项是符合题目要求的.
1.如图,四边形的斜二测画法的直观图为等腰梯形,已知,则下列说法正确的是( )
A.
B.
C.四边形的周长为
D.四边形的面积为
2.已知为虚部单位,复数为纯虚数,则的虚部为( )
A. B.1 C. D.-1
3.已知为虚数单位,,则复数在复平面上所对应的点在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
4.若复数满足,则( )
A. B.5 C. D.6
5.若圆锥的轴截面为等腰直角三角形,则它的底面积与侧面积之比是( )
A. B. C. D.
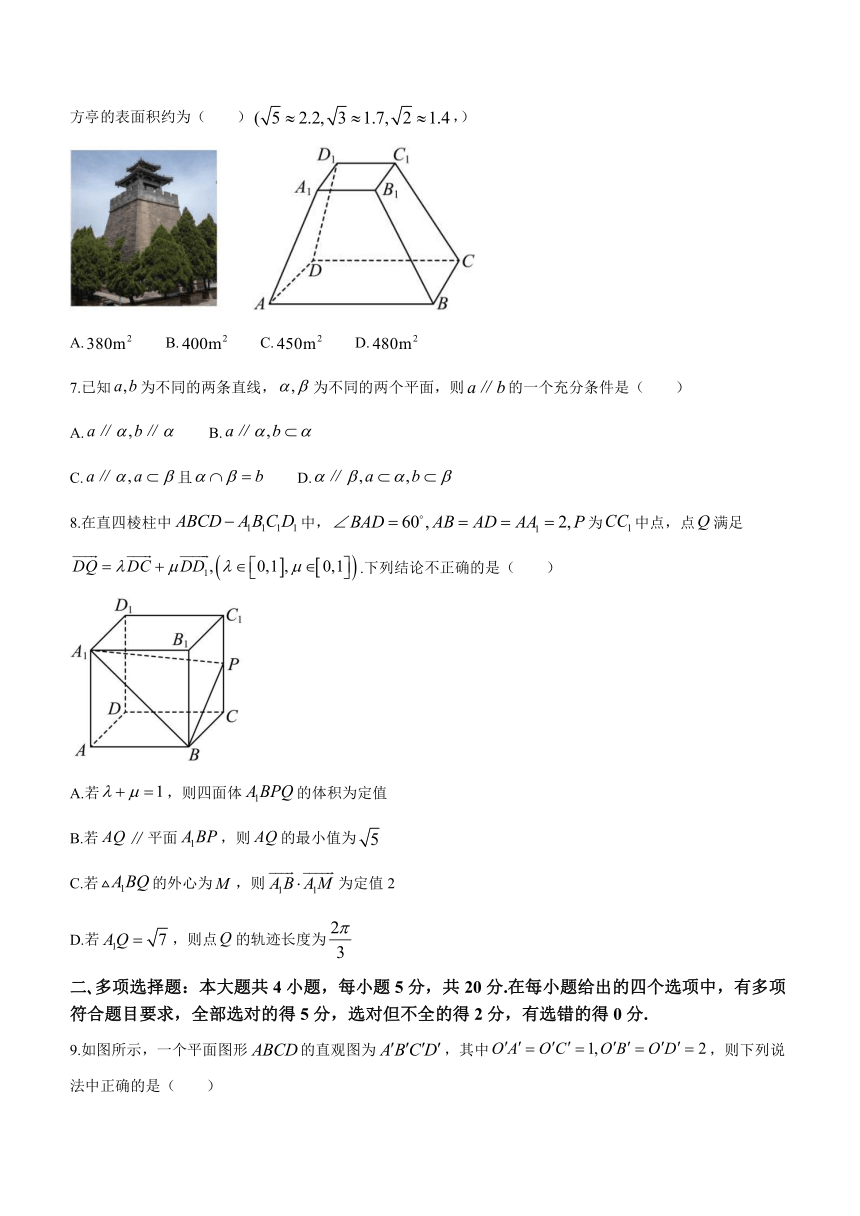
6.《九章算术》是我国古代的数学名著.其“商功”中记载:“正四面形棱台(即正四棱台)建筑物为方亭.”现有如图所示的烽火台,其主体部分为一方亭,将它的主体部分抽象成的正四棱台(如图所示),其中上底面与下底面的面积之比为,方亭的高为棱台上底面边长的3倍.已知方亭的体积为,则该方亭的表面积约为( ),)
A. B. C. D.
7.已知为不同的两条直线,为不同的两个平面,则的一个充分条件是( )
A. B.
C.且 D.
8.在直四棱柱中中,为中点,点满足.下列结论不正确的是( )
A.若,则四面体的体积为定值
B.若平面,则的最小值为
C.若的外心为,则为定值2
D.若,则点的轨迹长度为
二 多项选择题:本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求,全部选对的得5分,选对但不全的得2分,有选错的得0分.
9.如图所示,一个平面图形的直观图为,其中,则下列说法中正确的是( )
A.该平面图形是一个平行四边形但不是正方形
B.该平面图形的面积是8
C.该平面图形绕着直线旋转半周形成的几何体的体积是
D.以该平面图形为底,高为3的直棱柱的体对角线长为
10.已知复数,复数满足,则( )
A.
B.
C.复数在复平面内所对应的点的坐标是
D.复数在复平面内所对应的点为,则
11.下列有关复数的叙述正确的是( )
A.若,则
B.若,则的虚部为
C.若,则不可能为纯虚数
D.若复数满足,则
12.已知正方体的棱长为分别是的中点,则( )
A.
B.平面截此正方体所得截面的周长为
C.三棱锥的表面积为
D.三棱锥的体积为1
三 填空题:本大题共4个小题,每小题5分,共20分.
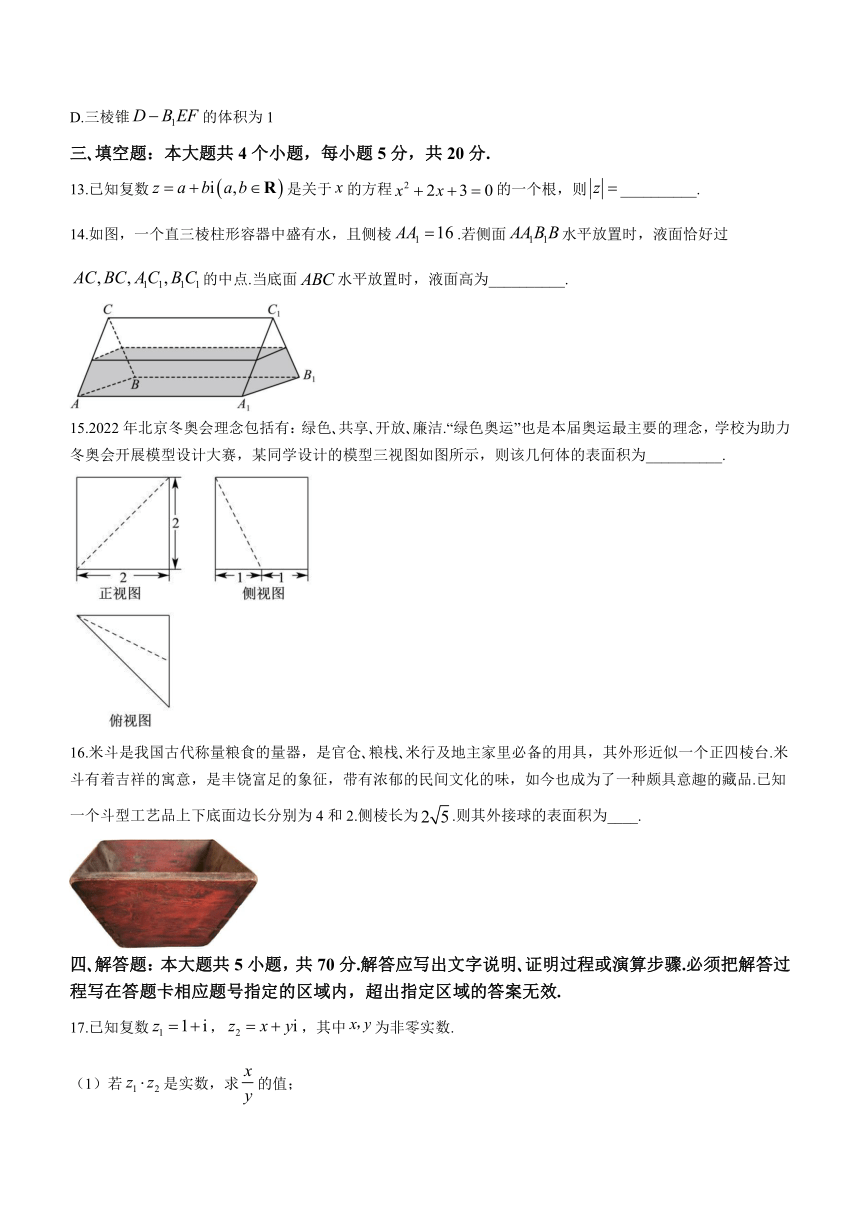
13.已知复数是关于的方程的一个根,则__________.
14.如图,一个直三棱柱形容器中盛有水,且侧棱.若侧面水平放置时,液面恰好过的中点.当底面水平放置时,液面高为__________.
15.2022年北京冬奥会理念包括有:绿色 共享 开放 廉洁.“绿色奥运”也是本届奥运最主要的理念,学校为助力冬奥会开展模型设计大赛,某同学设计的模型三视图如图所示,则该几何体的表面积为__________.
16.米斗是我国古代称量粮食的量器,是官仓 粮栈 米行及地主家里必备的用具,其外形近似一个正四棱台.米斗有着吉祥的寓意,是丰饶富足的象征,带有浓郁的民间文化的味,如今也成为了一种颇具意趣的藏品.已知一个斗型工艺品上下底面边长分别为4和2.侧棱长为.则其外接球的表面积为____.
四 解答题:本大题共5小题,共70分.解答应写出文字说明 证明过程或演算步骤.必须把解答过程写在答题卡相应题号指定的区域内,超出指定区域的答案无效.
17.已知复数,,其中为非零实数.
(1)若是实数,求的值;
(2)若,复数为纯虚数,求实数的值;
18.(1)计算;
(2)若实数x,y满足求x,y的值.
19.如图:在正方体中,为的中点.
(1)求三棱锥的体积;
(2)求证:平面;
(3)若为的中点,求证:平面平面.
20.如图,一个容器的盖子用一个正四棱台和一个球焊接而成,球的半径为R,正四棱台上 下底面边长分别为2.5R和3R,斜高为0.6R,取
(1)求这个盖子的表面积和体积(用R表示,焊接处对面积影响忽略不计)
(2)若R=2cm,为盖子涂色时所用的涂料每0.4kg可以涂1,计算100个这样的盖子涂色约需要涂料多少千克?(内部不涂色,结果精确到0.1千克)?
21.如图,四棱锥中,底面是平行四边形,为中点.
(1)求证:平面;
(2)若分别是线段的中点,是直线上的动点,则线段上是否存在点,使得平面?若存在,请求出的比值:若不存在,请说明理由.
22.如图所示,在四棱锥中,平面PAD,,E是PD的中点.
(1)求证:;
(2)线段AD上是否存在点N,使平面平面PAB,若不存在请说明理由:若存在给出证明.
聊城市第四中学2022-2023学年高一下学期5月月考
数学试题参考答案
一 单项选择题:本大题共8小题,每小题5分,共40分,在每小题给出四个选项中,只有一项是符合题目要求的.
1.D 2.D 3.B 4.A 5.A 6.C 7.D 8.C
二 多项选择题:本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求,全部选对的得5分,选对但不全的得2分,有选错的得0分.
9.BC 10.AD 11.ACD 12.BD
三 填空题:本大题共4个小题,每小题5分,共20分
13. 14.12 15. 16.
四 解答题:本大题共5小题,共70分.解答应写出文字说明 证明过程或演算步骤.必须把解答过程写在答题卡相应题号指定的区域内,超出指定区域的答案无效.
17.(1)∵为实数,
∴,
又∵为非零实数,
∴.
(2)∵,
∴,
∴为纯虚数,
∴
∴m的值为2.
18.【详解】(1)
;
(2),
即,
故,整理得,
所以,
解得.
19.(1)显然平面,于是.
(2)
设,连接,
在正方体中,四边形是正方形,是中点,
是的中点,,
平面平面
平面;
(2)为的中点,为的中点,
,
四边形为平行四边形,,
又平面平面平面,
由(2)知平面平面平面,
平面平面.
20.(1)因为球的半径为R,则该球的表面积为,该球的体积,
又四棱台的上 下底面边长分别为2.5R和3R,则四棱台的上 下底面积分别为和,
而正四棱台的斜高为0.6R,则四棱台的侧面积为,
正四棱台的高为上 下边长分别为2.5R和3R,腰长为0.6R的等腰梯形的高为,
正四棱台的体积,
所以容器盖子的表面积,
体积为().
(2)由(1)知,,当R=2cm时,()
所以100个这样的盖子约需涂料为().
21.【详解】
(1)证明:连接交于,再连接,
因为四边形为平行四边形,
所以为的中点,
又为的中点,
所以在中,,
又平面,平面,
所以平面.
(2)存在点G,使得平面.
与的交点记为.
当为的中点时,
可知,
所以,
M,N分别是线段的中点,
所以,
又,且平面,平面,
所以平面平面,又平面,
所以当为的中点时,
即时,平面.
22.【详解】
(1)因为平面,平面,平面平面,所以;
(2)存在,且当点是的中点时,平面平面.
下面给出证明:
因为 分别是 的中点,所以,
又平面,平面,所以平面.
由(1)知,,又是的中点,
,所以,所以四边形是平行四边形,从
而,
又平面,平面,所以平面.
又因为,所以,平面平面
数学试题
本试卷分选择题和非选择题两部分.满分150分.考试用时120分钟
一 单项选择题:本大题共8小题,每小题5分,共40分,在每小题给出四个选项中,只有一项是符合题目要求的.
1.如图,四边形的斜二测画法的直观图为等腰梯形,已知,则下列说法正确的是( )
A.
B.
C.四边形的周长为
D.四边形的面积为
2.已知为虚部单位,复数为纯虚数,则的虚部为( )
A. B.1 C. D.-1
3.已知为虚数单位,,则复数在复平面上所对应的点在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
4.若复数满足,则( )
A. B.5 C. D.6
5.若圆锥的轴截面为等腰直角三角形,则它的底面积与侧面积之比是( )
A. B. C. D.
6.《九章算术》是我国古代的数学名著.其“商功”中记载:“正四面形棱台(即正四棱台)建筑物为方亭.”现有如图所示的烽火台,其主体部分为一方亭,将它的主体部分抽象成的正四棱台(如图所示),其中上底面与下底面的面积之比为,方亭的高为棱台上底面边长的3倍.已知方亭的体积为,则该方亭的表面积约为( ),)
A. B. C. D.
7.已知为不同的两条直线,为不同的两个平面,则的一个充分条件是( )
A. B.
C.且 D.
8.在直四棱柱中中,为中点,点满足.下列结论不正确的是( )
A.若,则四面体的体积为定值
B.若平面,则的最小值为
C.若的外心为,则为定值2
D.若,则点的轨迹长度为
二 多项选择题:本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求,全部选对的得5分,选对但不全的得2分,有选错的得0分.
9.如图所示,一个平面图形的直观图为,其中,则下列说法中正确的是( )
A.该平面图形是一个平行四边形但不是正方形
B.该平面图形的面积是8
C.该平面图形绕着直线旋转半周形成的几何体的体积是
D.以该平面图形为底,高为3的直棱柱的体对角线长为
10.已知复数,复数满足,则( )
A.
B.
C.复数在复平面内所对应的点的坐标是
D.复数在复平面内所对应的点为,则
11.下列有关复数的叙述正确的是( )
A.若,则
B.若,则的虚部为
C.若,则不可能为纯虚数
D.若复数满足,则
12.已知正方体的棱长为分别是的中点,则( )
A.
B.平面截此正方体所得截面的周长为
C.三棱锥的表面积为
D.三棱锥的体积为1
三 填空题:本大题共4个小题,每小题5分,共20分.
13.已知复数是关于的方程的一个根,则__________.
14.如图,一个直三棱柱形容器中盛有水,且侧棱.若侧面水平放置时,液面恰好过的中点.当底面水平放置时,液面高为__________.
15.2022年北京冬奥会理念包括有:绿色 共享 开放 廉洁.“绿色奥运”也是本届奥运最主要的理念,学校为助力冬奥会开展模型设计大赛,某同学设计的模型三视图如图所示,则该几何体的表面积为__________.
16.米斗是我国古代称量粮食的量器,是官仓 粮栈 米行及地主家里必备的用具,其外形近似一个正四棱台.米斗有着吉祥的寓意,是丰饶富足的象征,带有浓郁的民间文化的味,如今也成为了一种颇具意趣的藏品.已知一个斗型工艺品上下底面边长分别为4和2.侧棱长为.则其外接球的表面积为____.
四 解答题:本大题共5小题,共70分.解答应写出文字说明 证明过程或演算步骤.必须把解答过程写在答题卡相应题号指定的区域内,超出指定区域的答案无效.
17.已知复数,,其中为非零实数.
(1)若是实数,求的值;
(2)若,复数为纯虚数,求实数的值;
18.(1)计算;
(2)若实数x,y满足求x,y的值.
19.如图:在正方体中,为的中点.
(1)求三棱锥的体积;
(2)求证:平面;
(3)若为的中点,求证:平面平面.
20.如图,一个容器的盖子用一个正四棱台和一个球焊接而成,球的半径为R,正四棱台上 下底面边长分别为2.5R和3R,斜高为0.6R,取
(1)求这个盖子的表面积和体积(用R表示,焊接处对面积影响忽略不计)
(2)若R=2cm,为盖子涂色时所用的涂料每0.4kg可以涂1,计算100个这样的盖子涂色约需要涂料多少千克?(内部不涂色,结果精确到0.1千克)?
21.如图,四棱锥中,底面是平行四边形,为中点.
(1)求证:平面;
(2)若分别是线段的中点,是直线上的动点,则线段上是否存在点,使得平面?若存在,请求出的比值:若不存在,请说明理由.
22.如图所示,在四棱锥中,平面PAD,,E是PD的中点.
(1)求证:;
(2)线段AD上是否存在点N,使平面平面PAB,若不存在请说明理由:若存在给出证明.
聊城市第四中学2022-2023学年高一下学期5月月考
数学试题参考答案
一 单项选择题:本大题共8小题,每小题5分,共40分,在每小题给出四个选项中,只有一项是符合题目要求的.
1.D 2.D 3.B 4.A 5.A 6.C 7.D 8.C
二 多项选择题:本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求,全部选对的得5分,选对但不全的得2分,有选错的得0分.
9.BC 10.AD 11.ACD 12.BD
三 填空题:本大题共4个小题,每小题5分,共20分
13. 14.12 15. 16.
四 解答题:本大题共5小题,共70分.解答应写出文字说明 证明过程或演算步骤.必须把解答过程写在答题卡相应题号指定的区域内,超出指定区域的答案无效.
17.(1)∵为实数,
∴,
又∵为非零实数,
∴.
(2)∵,
∴,
∴为纯虚数,
∴
∴m的值为2.
18.【详解】(1)
;
(2),
即,
故,整理得,
所以,
解得.
19.(1)显然平面,于是.
(2)
设,连接,
在正方体中,四边形是正方形,是中点,
是的中点,,
平面平面
平面;
(2)为的中点,为的中点,
,
四边形为平行四边形,,
又平面平面平面,
由(2)知平面平面平面,
平面平面.
20.(1)因为球的半径为R,则该球的表面积为,该球的体积,
又四棱台的上 下底面边长分别为2.5R和3R,则四棱台的上 下底面积分别为和,
而正四棱台的斜高为0.6R,则四棱台的侧面积为,
正四棱台的高为上 下边长分别为2.5R和3R,腰长为0.6R的等腰梯形的高为,
正四棱台的体积,
所以容器盖子的表面积,
体积为().
(2)由(1)知,,当R=2cm时,()
所以100个这样的盖子约需涂料为().
21.【详解】
(1)证明:连接交于,再连接,
因为四边形为平行四边形,
所以为的中点,
又为的中点,
所以在中,,
又平面,平面,
所以平面.
(2)存在点G,使得平面.
与的交点记为.
当为的中点时,
可知,
所以,
M,N分别是线段的中点,
所以,
又,且平面,平面,
所以平面平面,又平面,
所以当为的中点时,
即时,平面.
22.【详解】
(1)因为平面,平面,平面平面,所以;
(2)存在,且当点是的中点时,平面平面.
下面给出证明:
因为 分别是 的中点,所以,
又平面,平面,所以平面.
由(1)知,,又是的中点,
,所以,所以四边形是平行四边形,从
而,
又平面,平面,所以平面.
又因为,所以,平面平面
同课章节目录
