黑龙江大庆红岗区大庆铁人中学2022-2023学年高二下学期期中考试数学试题(含答案)
文档属性
| 名称 | 黑龙江大庆红岗区大庆铁人中学2022-2023学年高二下学期期中考试数学试题(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 447.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-11 00:00:00 | ||
图片预览





文档简介
大庆市重点中学2022-2023学年高二下学期期中考试
数学试题
试题说明:1、本试题满分150分,答题时间120分钟。
2、请将答案填写在答题卡上,考试结束后只交答题卡。
第Ⅰ卷 选择题部分
一、单选题(每小题只有一个选项正确,共8小题,每小题5分,共40分。)
1.已知数列为等差数列,且满足,,则的值为( )
A.2033 B.2123 C.0 D.123
2.设可导函数,则( )
A.-2 B.2 C. D.6
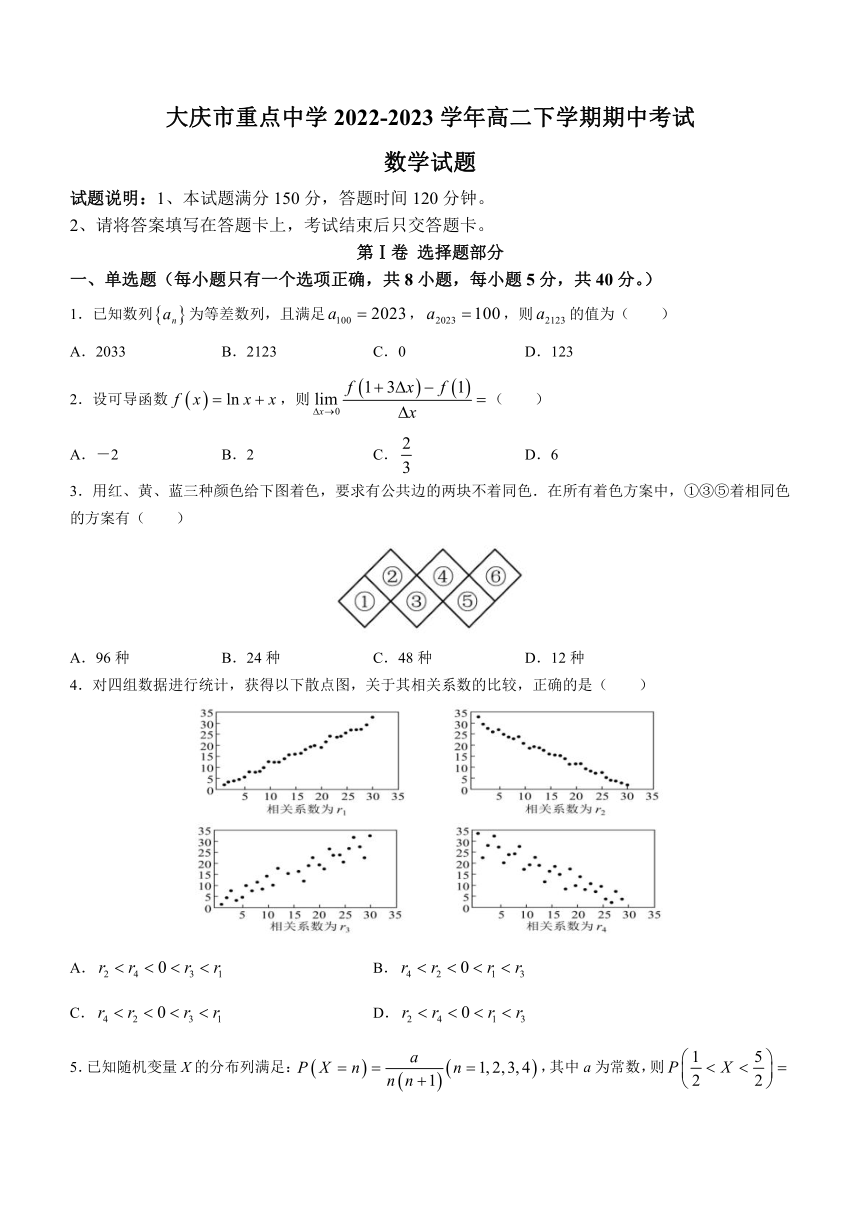
3.用红、黄、蓝三种颜色给下图着色,要求有公共边的两块不着同色.在所有着色方案中,①③⑤着相同色的方案有( )
A.96种 B.24种 C.48种 D.12种
4.对四组数据进行统计,获得以下散点图,关于其相关系数的比较,正确的是( )
A. B.
C. D.
5.已知随机变量X的分布列满足:,其中a为常数,则( )
A. B. C. D.
6.若,,则x+n=( )
A.5 B.3 C.6 D.2或5
7.用1、2、3、4、5组成没有重复数字的五位数,(代表万位,千位,百位,十位,个位依次为a,b,c,d,e)其中满足a>b>c<d<e的五位数有n个。则在的展开式中,的系数是( )
A.56 B.35 C.20 D.84
8.设,,c=1,则( )
A.a<b<c B.a<c<b C.b<a<c D.b<c<a
二、多选题(本题共4小题,共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,部分选对得得2分,有选错的得0分)
9.下列命题正确的是( )
A.对于事件A,B,若A B,且,,则
B.若随机变量且,则
C.若某种水果的果实横径X(单位:mm)服从正态分布,则果实横径在(65,80)的概率为0.7185(若,则)
D.已知随机变量,满足,若,,则,
10.若则下列结论正确的是( )
A. B.
C. D.
11.有3台车床加工同一型号的零件,第1,2,3台加工的次品率分别为6%,5%,4%,加工出来的零件混放在一起.已知第1,2,3台车床加工的零件数的比为5:6:9,现任取一个零件,记事件“零件为第i台车床加工”(i=1,2,3),事件B=“零件为次品”,则下列结论中正确的是( )
A. B.
C. D.
12.一个袋子中装有除颜色外完全相同的10个球,其中有6个黑球,4个白球,现从中任取4个球,记随机变量X为取出白球的个数,随机变量Y为取出黑球的个数,若取出一个白球得2分,取出一个黑球得1分,随机变量Z为取出4个球的总得分,则下列结论中不正确的是( )
A. B.X+Y=4 C.E(X)>E(Y) D.
三、填空题(本题共4小题,每小题5分,共20分)
13.某种机械设备的使用年限x(单位:年)与维修费y(单位:万元)的统计数据如下表所示:
使用年限x(单位:年) 1 2 3 4 5 6 7
维修费y(单位:万元) 2.90 3.30 3.60 4.40 4.80 5.20 5.90
由上表数据可知,y与x的相关系数为______.
(精确到0.01,参考公式和数据:,,,)
14.已知数列的前n项和是,且,若,则称项为“和谐项”,那么数列的所有“和谐项”的和为______.
15.河图是上古时代神话传说中伏羲通过黄河中浮出龙马身上的图案,与自己的观察,画出的“八卦”,而龙马身上的图案就叫做“河图”.把一到十分成五组,如图,其口诀:一六共宗,为水居北:二七同道,为火居南;三八为朋,为木居东;四九为友,为金居西;五十同途,为土居中.“河图”将一到十分成五行属性分别为金,木,水,火,土的五组,在五行的五种属性中,五行相克的规律为:金克木,木克土,土克水,水克火,火克金;五行相生的规律为:木生火,火生土,土生金,金生水,水生木.现从这十个数中随机抽取3个数,则这3个数字的属性互不相克的条件下,取到属性为土的数字的概率为______.
16.某高校大一新生中的6名同学打算参加学校组织的“雅荷文学社”、“青春风街舞社”、“羽乒协会”、“演讲团”、“吉他协会”五个社团,若每名同学必须参加且只能参加1个社团且每个社团至多两人参加,则这6个人中至多有1人参加“演讲团”的不同参加方法数为______.(用数字作答)
四、解答题(本题共6小题,共70分,解答应写出必要的文字说明、证明过程及演算步骤)
17.(10分)已知的展开式中第2项与第3项的二项式系数之比为2:5.
(1)求常数项;
(2)求系数最大的项.
18.(12分)数列满足,,,即
(1)求证:是等比数列;
(2)若,求的前n项和为.
19.(12分)某工厂车间有6台相同型号的机器,各台机器相互独立工作,工作时发生故障的概率都是,且一台机器的故障由一个维修工处理.已知此厂共有甲、乙、丙3名维修工,现有两种配备方案,方案一:由甲、乙、丙三人维护,每人负责2台机器;方案二:由甲乙两人共同维护6台机器,丙负责其他工作。
(1)对于方案一,设X为甲维护的机器某一时刻发生故障的台数,求X的分布列与数学期望E(X);
(2)在两种方案下,分别计算某一时刻机器发生故障时不能得到及时维修的概率,并以此为依据来判断,哪种方案能使工厂的生产效率更高?
20.(12分)已知.
(1)求的单调区间;
(2)若,记,为函数的两个极值点,求的取值范围.
21.(12分)某技术部门对工程师进行达标等级考核,需要进行两轮测试,每轮测试的成绩在90分及以上的定为该轮测试通过,只有通过第一轮测试的人员才能进行第二轮测试,两轮测试的过程及结果相互独立,并规定:①两轮测试均通过的定为一级工程师;②仅通过第一轮测试,而第二轮测试没通过的定为二级工程师;③第一轮测试没通过的不予定级.
现有某公司的甲、乙、丙三位工程师参加等级考核,已知他们通过第一轮测试的概率分别为,,,通过第二轮测试的概率均为.
(1)求经过本次考核,甲,乙,丙三位工程师中恰有两位被定为一级工程师的概率;
(2)公司为鼓励以上三名工程师参加等级考核设制两套奖励方案:
方案一:奖励定为一级工程师2000元,奖励定为二级工程师1500元,未定级给予鼓励奖500元;
方案二:获得一级或二级工程师均奖励2000元,未获得任何等级的不予奖励.
采用哪套方案,公司对于以上三人奖励支出会更少?
22.(12分)已知函数.
(1)当a=2时,求在x=0处的切线方程;
(2)若有两个零点,求a的取值范围;
(3)求证:
大庆市重点中学2022-2023学年高二下学期期中考试
数学答案
1 2 3 4 5 6 7 8 9 10 11 12
C D B A C D B D AD BC ACD AC
13.0.99 14.2047 15.0.4/ 16.5040
17.解:因为第二项与第三项的二项式系数之比是2:5,
则,即,解得n=0(舍)或n=6,所以n的值为6.
的展开式的通项为,
(1)当时,即k=4时,所以常数项为60.
(2)设第k+1项系数最大,由通项得
令,解得,又∵,∴k=2,
∴展开式中系数最大的项为第3项,且.
18.解:(1),,
∵,∴,
∴,又因为.
∴,
所以数列是以2为首项,2为公比的等比数列.
(2)由(1)可得,,,
设,设其前n项和为,
则,①
,②
①减②得:,
所以,所以.
19.解:(1)由题意可知,,
则,,,
所以,随机变量X的分布列如下表所示:
X 0 1 2
P
所以,.
(2)解:对于方案一:“机器发生故障时不能及时维修”等价于“甲、乙、丙三人中,至少有一人负责的2台机器同时发生故障”,考查反面处理这个问题.
设机器发生故障时不能及时维修的概率为,则其概率为.
对于方案二:设机器发生故障时不能及时维修的概率为,则
,
所以,,即方案二能让故障机器更大概率得到及时维修,使得工厂的生产效率更高.
20.解:(1),(x>0),令,则,
当时,,的单调减区间为.
当时,,的单调增区间为.
综上所述,的单调减区间为,的单调增区间为.
(2),,(x>0),
∵,为两个极值点,∴有两个不等的正根,,
∴,,,,得,
,
令,(t>1),得,
,因为t>1,则,则,
∴在(1,+∞)递减,∴,
即的取值范围为.
21.解:(1)设甲,乙,丙被定为一级工程师的事件分别为,,,
事件C表示三位工程师中恰有两位被定为一级工程师.
,
所以
经过本次考核,甲,乙,丙三位工程师中恰有两位被定为一级工程师的概率为
(2)方案一:设甲,乙,丙获得的奖金分别为X,Y,Z,则X,Y,Z的取值均为2000,1500,500;
则,,;
故
,
,
,
;
.
方案二:设甲,乙,丙获得的奖金分别为,,,则,,的取值均为2000,0;
,;
,,
显然,从奖励期望值角度看,公司采用方案二,奖励支出会更少.
22.解:(1)当a=2时,则,,
可得,,
即切点坐标为(0,2),斜率k=3,所以切线方程y=3x+2.
(2)由题意可得:,
因为,则有:
(i)当a≤0时,则,即,
所以在R上单调递减,至多有1个零点,不合题意;
(ⅱ)当a>0时,令时,则;令时,则;
则在上单调递增,在上单调递减,
且当x趋近于-∞时,趋近于+∞,当x趋近于+∞时,趋近于+∞,
若有两个零点,则,
构建,则在(0,+∞)上单调递增,且,
若,则0<a<1;综上所述:a的取值范围为(0,1).
(3)由(2)可知:当a=1时,在(0,+∞)上单调递增,在(-∞,0)上单调递减,
则,
可得,当且仅当x=0时,等号成立;
构建,则,
构建,则,
构建,则,
令,解得x>1;令,解得x<1;
则在(1,+∞)上单调递增,在(-∞,1)上单调递减,所以,
即恒成立,则在R上单调递增,且,
令,解得x>1;令,解得x<1;
即当x>1时,;当x<1时,;
则在(1,+∞)上单调递增,在(-∞,1)上单调递减,所以,
所以,当且仅当x=1时,等号成立;
综上所述:等号不能同时取到,所以.
数学试题
试题说明:1、本试题满分150分,答题时间120分钟。
2、请将答案填写在答题卡上,考试结束后只交答题卡。
第Ⅰ卷 选择题部分
一、单选题(每小题只有一个选项正确,共8小题,每小题5分,共40分。)
1.已知数列为等差数列,且满足,,则的值为( )
A.2033 B.2123 C.0 D.123
2.设可导函数,则( )
A.-2 B.2 C. D.6
3.用红、黄、蓝三种颜色给下图着色,要求有公共边的两块不着同色.在所有着色方案中,①③⑤着相同色的方案有( )
A.96种 B.24种 C.48种 D.12种
4.对四组数据进行统计,获得以下散点图,关于其相关系数的比较,正确的是( )
A. B.
C. D.
5.已知随机变量X的分布列满足:,其中a为常数,则( )
A. B. C. D.
6.若,,则x+n=( )
A.5 B.3 C.6 D.2或5
7.用1、2、3、4、5组成没有重复数字的五位数,(代表万位,千位,百位,十位,个位依次为a,b,c,d,e)其中满足a>b>c<d<e的五位数有n个。则在的展开式中,的系数是( )
A.56 B.35 C.20 D.84
8.设,,c=1,则( )
A.a<b<c B.a<c<b C.b<a<c D.b<c<a
二、多选题(本题共4小题,共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,部分选对得得2分,有选错的得0分)
9.下列命题正确的是( )
A.对于事件A,B,若A B,且,,则
B.若随机变量且,则
C.若某种水果的果实横径X(单位:mm)服从正态分布,则果实横径在(65,80)的概率为0.7185(若,则)
D.已知随机变量,满足,若,,则,
10.若则下列结论正确的是( )
A. B.
C. D.
11.有3台车床加工同一型号的零件,第1,2,3台加工的次品率分别为6%,5%,4%,加工出来的零件混放在一起.已知第1,2,3台车床加工的零件数的比为5:6:9,现任取一个零件,记事件“零件为第i台车床加工”(i=1,2,3),事件B=“零件为次品”,则下列结论中正确的是( )
A. B.
C. D.
12.一个袋子中装有除颜色外完全相同的10个球,其中有6个黑球,4个白球,现从中任取4个球,记随机变量X为取出白球的个数,随机变量Y为取出黑球的个数,若取出一个白球得2分,取出一个黑球得1分,随机变量Z为取出4个球的总得分,则下列结论中不正确的是( )
A. B.X+Y=4 C.E(X)>E(Y) D.
三、填空题(本题共4小题,每小题5分,共20分)
13.某种机械设备的使用年限x(单位:年)与维修费y(单位:万元)的统计数据如下表所示:
使用年限x(单位:年) 1 2 3 4 5 6 7
维修费y(单位:万元) 2.90 3.30 3.60 4.40 4.80 5.20 5.90
由上表数据可知,y与x的相关系数为______.
(精确到0.01,参考公式和数据:,,,)
14.已知数列的前n项和是,且,若,则称项为“和谐项”,那么数列的所有“和谐项”的和为______.
15.河图是上古时代神话传说中伏羲通过黄河中浮出龙马身上的图案,与自己的观察,画出的“八卦”,而龙马身上的图案就叫做“河图”.把一到十分成五组,如图,其口诀:一六共宗,为水居北:二七同道,为火居南;三八为朋,为木居东;四九为友,为金居西;五十同途,为土居中.“河图”将一到十分成五行属性分别为金,木,水,火,土的五组,在五行的五种属性中,五行相克的规律为:金克木,木克土,土克水,水克火,火克金;五行相生的规律为:木生火,火生土,土生金,金生水,水生木.现从这十个数中随机抽取3个数,则这3个数字的属性互不相克的条件下,取到属性为土的数字的概率为______.
16.某高校大一新生中的6名同学打算参加学校组织的“雅荷文学社”、“青春风街舞社”、“羽乒协会”、“演讲团”、“吉他协会”五个社团,若每名同学必须参加且只能参加1个社团且每个社团至多两人参加,则这6个人中至多有1人参加“演讲团”的不同参加方法数为______.(用数字作答)
四、解答题(本题共6小题,共70分,解答应写出必要的文字说明、证明过程及演算步骤)
17.(10分)已知的展开式中第2项与第3项的二项式系数之比为2:5.
(1)求常数项;
(2)求系数最大的项.
18.(12分)数列满足,,,即
(1)求证:是等比数列;
(2)若,求的前n项和为.
19.(12分)某工厂车间有6台相同型号的机器,各台机器相互独立工作,工作时发生故障的概率都是,且一台机器的故障由一个维修工处理.已知此厂共有甲、乙、丙3名维修工,现有两种配备方案,方案一:由甲、乙、丙三人维护,每人负责2台机器;方案二:由甲乙两人共同维护6台机器,丙负责其他工作。
(1)对于方案一,设X为甲维护的机器某一时刻发生故障的台数,求X的分布列与数学期望E(X);
(2)在两种方案下,分别计算某一时刻机器发生故障时不能得到及时维修的概率,并以此为依据来判断,哪种方案能使工厂的生产效率更高?
20.(12分)已知.
(1)求的单调区间;
(2)若,记,为函数的两个极值点,求的取值范围.
21.(12分)某技术部门对工程师进行达标等级考核,需要进行两轮测试,每轮测试的成绩在90分及以上的定为该轮测试通过,只有通过第一轮测试的人员才能进行第二轮测试,两轮测试的过程及结果相互独立,并规定:①两轮测试均通过的定为一级工程师;②仅通过第一轮测试,而第二轮测试没通过的定为二级工程师;③第一轮测试没通过的不予定级.
现有某公司的甲、乙、丙三位工程师参加等级考核,已知他们通过第一轮测试的概率分别为,,,通过第二轮测试的概率均为.
(1)求经过本次考核,甲,乙,丙三位工程师中恰有两位被定为一级工程师的概率;
(2)公司为鼓励以上三名工程师参加等级考核设制两套奖励方案:
方案一:奖励定为一级工程师2000元,奖励定为二级工程师1500元,未定级给予鼓励奖500元;
方案二:获得一级或二级工程师均奖励2000元,未获得任何等级的不予奖励.
采用哪套方案,公司对于以上三人奖励支出会更少?
22.(12分)已知函数.
(1)当a=2时,求在x=0处的切线方程;
(2)若有两个零点,求a的取值范围;
(3)求证:
大庆市重点中学2022-2023学年高二下学期期中考试
数学答案
1 2 3 4 5 6 7 8 9 10 11 12
C D B A C D B D AD BC ACD AC
13.0.99 14.2047 15.0.4/ 16.5040
17.解:因为第二项与第三项的二项式系数之比是2:5,
则,即,解得n=0(舍)或n=6,所以n的值为6.
的展开式的通项为,
(1)当时,即k=4时,所以常数项为60.
(2)设第k+1项系数最大,由通项得
令,解得,又∵,∴k=2,
∴展开式中系数最大的项为第3项,且.
18.解:(1),,
∵,∴,
∴,又因为.
∴,
所以数列是以2为首项,2为公比的等比数列.
(2)由(1)可得,,,
设,设其前n项和为,
则,①
,②
①减②得:,
所以,所以.
19.解:(1)由题意可知,,
则,,,
所以,随机变量X的分布列如下表所示:
X 0 1 2
P
所以,.
(2)解:对于方案一:“机器发生故障时不能及时维修”等价于“甲、乙、丙三人中,至少有一人负责的2台机器同时发生故障”,考查反面处理这个问题.
设机器发生故障时不能及时维修的概率为,则其概率为.
对于方案二:设机器发生故障时不能及时维修的概率为,则
,
所以,,即方案二能让故障机器更大概率得到及时维修,使得工厂的生产效率更高.
20.解:(1),(x>0),令,则,
当时,,的单调减区间为.
当时,,的单调增区间为.
综上所述,的单调减区间为,的单调增区间为.
(2),,(x>0),
∵,为两个极值点,∴有两个不等的正根,,
∴,,,,得,
,
令,(t>1),得,
,因为t>1,则,则,
∴在(1,+∞)递减,∴,
即的取值范围为.
21.解:(1)设甲,乙,丙被定为一级工程师的事件分别为,,,
事件C表示三位工程师中恰有两位被定为一级工程师.
,
所以
经过本次考核,甲,乙,丙三位工程师中恰有两位被定为一级工程师的概率为
(2)方案一:设甲,乙,丙获得的奖金分别为X,Y,Z,则X,Y,Z的取值均为2000,1500,500;
则,,;
故
,
,
,
;
.
方案二:设甲,乙,丙获得的奖金分别为,,,则,,的取值均为2000,0;
,;
,,
显然,从奖励期望值角度看,公司采用方案二,奖励支出会更少.
22.解:(1)当a=2时,则,,
可得,,
即切点坐标为(0,2),斜率k=3,所以切线方程y=3x+2.
(2)由题意可得:,
因为,则有:
(i)当a≤0时,则,即,
所以在R上单调递减,至多有1个零点,不合题意;
(ⅱ)当a>0时,令时,则;令时,则;
则在上单调递增,在上单调递减,
且当x趋近于-∞时,趋近于+∞,当x趋近于+∞时,趋近于+∞,
若有两个零点,则,
构建,则在(0,+∞)上单调递增,且,
若,则0<a<1;综上所述:a的取值范围为(0,1).
(3)由(2)可知:当a=1时,在(0,+∞)上单调递增,在(-∞,0)上单调递减,
则,
可得,当且仅当x=0时,等号成立;
构建,则,
构建,则,
构建,则,
令,解得x>1;令,解得x<1;
则在(1,+∞)上单调递增,在(-∞,1)上单调递减,所以,
即恒成立,则在R上单调递增,且,
令,解得x>1;令,解得x<1;
即当x>1时,;当x<1时,;
则在(1,+∞)上单调递增,在(-∞,1)上单调递减,所以,
所以,当且仅当x=1时,等号成立;
综上所述:等号不能同时取到,所以.
同课章节目录
