期末必考专题:长方体(二)(单元测试)-小学数学五年级下册北师大版(含答案)
文档属性
| 名称 | 期末必考专题:长方体(二)(单元测试)-小学数学五年级下册北师大版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-12 21:31:22 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期末必考专题:长方体(二)(单元测试)-小学数学五年级下册北师大版
一、选择题
1.下面几种包装的食用油,买( )比较划算。
A. B. C. D.
2.一个矿泉水瓶的容积大约是550( )。
A.毫升 B.立方米 C.升 D.立方分米
3.一个正方体的棱长扩大到原来的4倍,它的体积扩大到原来的( )。
A.16倍 B.8倍 C.64倍 D.4倍
4.一根长方体木料的长是1.2米,沿着横截面锯成3段,表面积增加24平方厘米,原来这根木料的体积是( )立方厘米。
A.480 B.28.8 C.720 D.864
5.将一个长方体的高截去5cm就变成了正方体(如图),正方体的表面积比原长方体的表面积减少了60cm2,原长方体的体积是( )立方厘米。
A.27 B.36 C.64 D.72
6.下图中的长方体盒子最多能装( )个这样的小正方体。
A.12 B.18 C.30 D.36
二、填空题
7.在括号里填上合适的单位。
牙膏盒的体积约50( );文具盒的体积约0.35( );
一个热水瓶的容积约2( );一瓶矿泉水的容积是500( )。
8.1.2m3=( )dm3 280cm3=( )dm3 0.6dm3=( )ml
9.如图:每个棱长是1厘米的小正方体堆在墙角处,露在外面的小正方体的面有( )个,露在外面的面积是( )平方厘米,要想补成一个大正方体,至少还需要( )个小正方体。
10.一个正方体的总棱长是216厘米,这个正方体的表面积是( )平方厘米,体积是( )立方厘米。
11.把40颗黄豆放入有水的量杯中(完全浸没),观察水面数据如表,平均每颗黄豆的体积是( )cm3。
放入前 放入后
180mL 204mL
12.一个长方体鱼缸的容积是288L,从里面量这个鱼缸的高正好是0.6m,鱼缸的占地面积是( )m2。
三、判断题
13.棱长是6的正方体体积和表面积一样大。( )
14.一瓶墨水约有60升。( )
15.两个长方体体积相等,表面积也一定相等。( )
16.体积是1dm3的正方体,可以分成10000个棱长是1cm的小正方体。( )
17.把长方体形状的橡皮泥捏成一个正方体,它的形状变了,但体积不变。( )
四、图形计算
18.求出下面图形的表面积和体积。
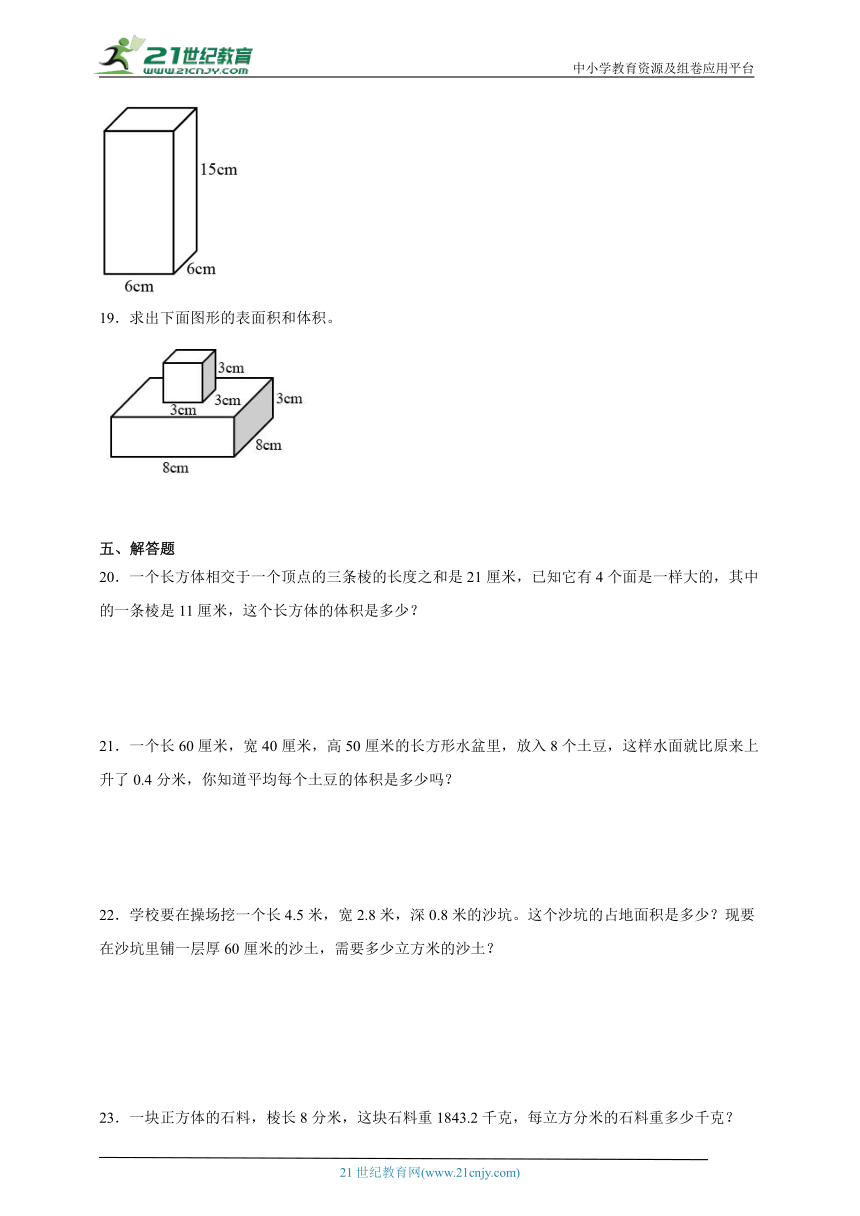
19.求出下面图形的表面积和体积。
五、解答题
20.一个长方体相交于一个顶点的三条棱的长度之和是21厘米,已知它有4个面是一样大的,其中的一条棱是11厘米,这个长方体的体积是多少?
21.一个长60厘米,宽40厘米,高50厘米的长方形水盆里,放入8个土豆,这样水面就比原来上升了0.4分米,你知道平均每个土豆的体积是多少吗?
22.学校要在操场挖一个长4.5米,宽2.8米,深0.8米的沙坑。这个沙坑的占地面积是多少?现要在沙坑里铺一层厚60厘米的沙土,需要多少立方米的沙土?
23.一块正方体的石料,棱长8分米,这块石料重1843.2千克,每立方分米的石料重多少千克?
24.一个无盖的长方体玻璃鱼缸长4分米,宽2.5分米,高6分米。
(1)要制作这样一个鱼缸,至少需玻璃多少平方分米?
(2)35升水倒入这个鱼缸中,水面距离玻璃鱼缸容器口多少分米?
(3)在这个鱼缸中放了30条小金鱼后,水面上升了0.24厘米。每条小金鱼的体积是多少立方厘米?
参考答案:
1.C
【分析】根据单位之间的换算,大单位换算成小单位要乘它们之间的进率;小单位换算成大单位要除以它们之间的进率即可解答。
【详解】A.180mL=0.18L,10÷0.18≈55.56(元/L)
B.900mL=0.9L,42÷0.9≈46.67(元/L)
C.155÷5=31(元/L)
D.200÷6≈33.33(元/L)
55.56>46.67>33.33>31
因此几种包装的食用油,比较划算。
故答案为:C
【点睛】本题主要考查单位之间的换算,大单位换算成小单位要乘它们之间的进率;小单位换算成大单位要除以它们之间的进率。
2.A
【分析】根据生活经验、数据大小及对单位的认识可知:计量矿泉水瓶的容积用“毫升”作单位;据此解答。
【详解】由分析可得:一个矿泉水瓶的容积大约是550毫升。
故答案为:A
【点睛】联系生活实际,根据计量单位和数据的大小,灵活选择合适的计量单位。
3.C
【分析】根据正方体的体积=棱长×棱长×棱长以及积的变化规律,我们可以得到,一个正方体的棱长扩大到原来的4倍,它的体积扩大到原来的(4×4×4)倍。据此解答。
【详解】4×4×4
=16×4
=64
一个正方体的棱长扩大到原来的4倍,它的体积扩大到原来的64倍。
故答案为:C
【点睛】本题考查了正方体的体积及积的变化规律,解题关键是熟记体积公式。
4.C
【分析】根据题意可知,把这个长方体木料锯成3段,表面积增加了24平方厘米,表面积增加的是4个截面的面积,据此可以求出长方体木料的底面积,再根据长方体的体积公式:V=Sh,把数据代入公式解答。
【详解】1.2米=120厘米
24÷4×120
=6×120
=720(立方厘米)
这根长方体木料的体积是720立方厘米。
故答案为:C
【点睛】此题主要考查长方体的表面积公式、体积公式的灵活运用,关键是熟记公式。
5.D
【分析】根据高减少5cm,就剩下一个正方体可知,这个正方体比原长方体表面积减少的4个面是相同的,根据已知表面积减少了60cm2,60÷4÷5=3cm,求出减少面的宽,也就是剩下的正方体的棱长,然后3+5=8(cm)求出原长方体的高,再计算原长方体的体积即可。
【详解】减少的面的宽(剩下正方体的棱长)
60÷4÷5
=15÷5
=3(cm)
原长方体的高3+5=8(cm)
原长方体体积为:
3×3×8
=9×8
=72(cm3)
原来长方体的体积是72cm3。
故答案为:D
【点睛】根据截去后剩下是正方体,可知减少的部分是宽为3cm的4个面,从而可以分别求出长方体的长、宽、高,进而利用长方体的体积的计算方法即可求解。
6.D
【分析】观察图形可知,沿长方体盒子的长摆了4个小正方体,沿盒子的宽摆了3个小正方体,沿盒子的高摆了3个小正方体,根据长方体体积公式:体积=长×宽×高,求出这个长方体盒子最多能装小正方体的个数。
【详解】4×3×3
=12×3
=36(个)
下图中的长方体盒子最多能装36个小正方体。
故答案为:D
【点睛】分析出长、宽、高各摆了几个小正方体。再运用长方体体积公式进行解答。
7. 立方厘米/cm3 立方分米/dm3 升/L 毫升/mL
【分析】根据生活经验以及数据的大小,选择合适的计量单位,即可解答。
【详解】牙膏盒的体积约50立方厘米;
文具盒的体积约0.35立方分米;
一个热水瓶的容积约2升;
一瓶矿泉水的容积是500毫升。
【点睛】此题考查根据情景选择合适的计量单位,要注意联系生活实际、计量单位和数据的大小,灵活的选择。
8. 1200 0.28 600
【分析】1m3=1000dm3;1dm3=1000cm3;1dm3=1000mL;高度单位换算成低级单位,乘进率;低级单位换算成高级单位,除以进率;据此解答。
【详解】1.2m3=1200dm3
280cm3=0.28dm3
0.6dm3=600mL
【点睛】熟记进率是解答本题的关键。
9. 12 12 21
【分析】根据三视图可知,露在外面的面一共有(4+5+3)个,根据正方形的面积公式,可知一个正方形面的面积是1平方厘米,进而求出露在外面的面有多少平方厘米,要想补成一个大正方体,至少可以补成一个棱长为3厘米的正方体,根据正方体的体积公式,用3×3×3即可求出大正方体的体积,然后除以小正方体的体积,即可求出小正方体的个数,再减去原来小正方体个数,即可求出要想补成一个大正方体,至少还需要多少个小正方体。
【详解】4+5+3=12(个)
1×1×12=12(平方厘米)
(3×3×3)÷(1×1×1)
=27÷1
=27(个)
27-6=21(个)
每个棱长是1厘米的小正方体堆在墙角处,露在外面的小正方体的面有12个,露在外面的面积是12平方厘米,要想补成一个大正方体,至少还需要21个小正方体。
【点睛】解答本题的关键是数出有几个露在外面的面。
10. 1944 5832
【分析】根据正方体的棱长和=棱长×12,用216÷12即可求出正方体的棱长,然后根据正方体的表面积=棱长×棱长×6,正方体的体积=棱长×棱长×棱长,代入数据解答。
【详解】216÷12=18(厘米)
18×18×6
=324×6
=1944(平方厘米)
18×18×18
=324×18
=5832(立方厘米)
这个正方体的表面积是1944平方厘米,体积是5832立方厘米。
【点睛】本题考查了正方体的棱长和公式、表面积公式、体积公式的应用,要熟练掌握公式。
11.0.6
【分析】用放入后的容积减去放入前的容积,求出40粒黄豆的体积,再除以40,即可求出1粒黄豆的体积。
【详解】204-180=24(mL)
24mL=24 cm3
24÷40=0.6(cm3)
均每颗黄豆的体积是0.6cm3。
【点睛】本题考查利用排水法测量不规则物体的体积。
12.0.48
【分析】首先把288L换算成0.288m3,根据长方体的容积(体积)公式:V=Sh,那么S=V÷h,把数据代入公式解答。
【详解】288L=0.288m3
0.288÷0.6=0.48(m2)
鱼缸的占地面积是0.48m2。
【点睛】此题主要考查长方体的容积(体积)公式的灵活运用,关键是熟记公式,注意:容积单位与体积之间的换算。
13.×
【分析】根据正方体的表面积公式:表面积=棱长×棱长×6,体积公式:体积=棱长×棱长×棱长,因为表面积和体积不是同类量,所以它们不能进行比较。
【详解】根据分析可知,表面积和体积不是同类量,所以它们不能进行比较;
棱长是6的正方体体积和表面积无法比较。
原题干说法错误。
故答案为:×
【点睛】本题考查的目的是理解正方体的表面积、体积的意义,明确:表面积和体积不是同类量,所以它们不能进行比较,能进行比较的只有同类量。
14.×
【分析】根据生活经验以及数据的大小,选择合适的计量单位,即可解答。
【详解】一瓶墨水约有60毫升,原题说法错误。
故答案为:×
【点睛】此题考查根据情景选择合适的计量单位,要注意联系生活实际、计量单位和数据的大小,灵活地选择。
15.×
【分析】长方体的表面积=(长×宽+长×高+宽×高)×2,长方体的体积=长×宽×高,据此解答。
【详解】根据题意,若一个长方体的长宽高为6厘米,8厘米,10厘米,另一个长宽高为4厘米,10厘米,12厘米;
体积分别为:
6×8×10
=48×10
=480(立方厘米)
4×10×12
=40×12
=480(立方厘米)
表面积分别为:
(6×8+8×10+6×10)×2
=(48+80+60)×2
=(128+60)×2
=188×2
=376(平方厘米)
(4×10+10×12+4×12)×2
=(40+120+48)×2
=(160+48)×2
=208×2
=416(平方厘米)
两个长方体的体积都是480立方厘米,体积相等,表面积不相等。
故答案为:×
【点睛】本题考查了长方体的体积和表面积公式。
16.×
【分析】根据正方体体积公式:体积=棱长×棱长×棱长,代入数据,求出棱长是1厘米的正方体的体积,再用体积是1dm3正方体的体积÷棱长是1cm正方体的体积,即可求出可以分成多少个棱长是1cm的正方体,再进行判断。
【详解】1dm3=1000cm3
1000÷(1×1×1)
=1000÷(1×1)
=1000÷1
=1000(个)
体积是1dm3的正方体,可以分成1000个棱长是1cm的小正方体。
原题干说法错误。
故答案为:×
【点睛】本题考查立体图形的切拼,以及正方体体积公式的应用,注意单位名数的统一。
17.√
【详解】把一个长方体的橡皮泥捏成正方体,长方体和正方体的体积都是这块橡皮泥的体积,但是六个面的形状发生了变化,表面积变了。比如:将一个长10厘米,宽5厘米、高5厘米的长方体橡皮泥捏成一个正方体,橡皮泥的体积都是10×5×5=250立方厘米,形状由长方体变为正方体,所以把长方体形状的橡皮泥捏成一个正方体,它的形状变了,但体积不变。原说法正确。
故答案为:√
18.表面积:432cm2;体积:540cm3
【分析】根据长方体表面积公式:表面积=(长×宽+长×高+宽×高)×2;长方体体积公式:体积=长×宽×高,代入数据,即可解答。
【详解】(6×6+6×15+6×15)×2
=(36+90+90)×2
=(126+90)×2
=216×2
=432(cm2)
6×6×15
=36×15
=540(cm3)
19.表面积:260cm2;体积:219cm3
【分析】表面积=长是8cm,宽是8cm,高是3cm的长方体的表面积+棱长是3cm的侧面积;根据长方体表面积公式:表面积=(长×宽+长×高+宽×高)×2;正方体侧面积公式:棱长×棱长×4,代入数据,即可解答。
体积=长是8cm,宽是8cm,高是3cm的长方体的体积+棱长是3cm的正方体的体积;根据长方体的体积公式:体积=长×宽×高;正方体体积公式:体积=棱长×棱长×棱长,代入数据,即可解答。
【详解】表面积:(8×8+8×3+8×3)×2+3×3×4
=(64+24+24)×2+9×4
=(88+24)×2+36
=112×2+36
=224+36
=260(cm2)
体积:8×8×3+3×3×3
=64×3+9×3
=192+27
=219(cm3)
20.275立方厘米
【分析】一个长方体相交与一个顶点的三条棱的长度之和是21厘米,则长+宽+高=21厘米,已知它有4个面是一样大的,则长、宽、高中有2个棱是相等的,因为11+11=22,所以不能有2个11厘米,所以另外两个棱相等;用21-11求出另外两条棱的和,再除以2,求出一条棱的长度,再根据长方体体积公式:体积=长×宽×高,代入数据,即可解答。
【详解】(21-11)÷2
=10÷2
=5(厘米)
11×5×5
=55×5
=275(立方厘米)
答:这个长方体的体积是275立方厘米。
【点睛】本体考查长方体特征以及长方体体积公式的应用,关键是熟记公式。
21.1200立方厘米
【分析】根据不规则物体的体积公式:容器的底面积×水面变化的高度=不规则物体的体积,再除以8即可求出平均每个土豆的体积。
【详解】0.4分米=4厘米
60×40×4=9600(立方厘米)
9600÷8=1200(立方厘米)
答:平均每个土豆的体积是1200立方厘米。
【点睛】本题主要考查不规则物体体积公式,熟练掌握它的公式并灵活运用。
22.12.6平方米;7.56立方米
【分析】占地面积就是底面面积;用底面积乘沙土厚度,注意单位要统一;根据长方体的容积(体积)公式:V=abh,把数据代入公式解答。
【详解】4.5×2.8=12.6(平方米)
60厘米=0.6米
12.6×0.6=7.56(立方米)
答:这个沙坑的占地面积是12.6平方米,需要7.56立方米的沙土。
【点睛】本题主要考查长方体体积的计算。
23.3.6千克
【分析】根据正方体的体积=棱长×棱长×棱长,用8×8×8即可求出石料的体积,然后用1843.2千克除以石料的体积即可求出每立方分米的石料重多少千克。
【详解】1843.2÷(8×8×8)
=1843.2÷512
=3.6(千克)
答:每立方分米的石料重3.6千克。
【点睛】本题主要考查了正方体体积公式的灵活应用。
24.(1)88平方分米;(2)2.5分米;(3)8立方厘米
【分析】(1)无盖的长方体表面积只有5个面的面积,根据无盖的长方体面积=长×宽+长×高×2+宽×高×2,用4×2.5+4×6×2+2.5×6×2即可求出无盖的长方体鱼缸的表面积。
(2)35升=35立方分米,根据长方体的体积=长×宽×高,用35÷4÷2.5即可求出水的高度,然后用鱼缸的高度减去水的高度,即可求出水面距离玻璃鱼缸容器口多少分米;
(3)0.24厘米=0.024分米,根据物体的体积=上升部分水的体积,物体的体积=长×宽×上升部分的高度,用4×2.5×0.024即可求出30条金鱼的体积。然后把结果化为立方厘米,再根据除法的意义,用鱼的总体积除以30,即可求出每条鱼的体积,据此解答。
【详解】(1)4×2.5+4×6×2+2.5×6×2
=10+48+30
=88(平方分米)
答:要制作这样一个鱼缸,至少需玻璃88平方分米。
(2)35升=35立方分米
35÷4÷2.5=3.5(分米)
6-3.5=2.5(分米)
答:水面距离玻璃鱼缸容器口2.5分米。
(3)0.24厘米=0.024分米
4×2.5×0.024=0.24(立方分米)
0.24立方分米=240立方厘米
240÷30=8(立方厘米)
答:每条小金鱼的体积是8立方厘米。
【点睛】本题主要考查了长方体表面积公式、体积公式的灵活应用,要注意统一单位。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末必考专题:长方体(二)(单元测试)-小学数学五年级下册北师大版
一、选择题
1.下面几种包装的食用油,买( )比较划算。
A. B. C. D.
2.一个矿泉水瓶的容积大约是550( )。
A.毫升 B.立方米 C.升 D.立方分米
3.一个正方体的棱长扩大到原来的4倍,它的体积扩大到原来的( )。
A.16倍 B.8倍 C.64倍 D.4倍
4.一根长方体木料的长是1.2米,沿着横截面锯成3段,表面积增加24平方厘米,原来这根木料的体积是( )立方厘米。
A.480 B.28.8 C.720 D.864
5.将一个长方体的高截去5cm就变成了正方体(如图),正方体的表面积比原长方体的表面积减少了60cm2,原长方体的体积是( )立方厘米。
A.27 B.36 C.64 D.72
6.下图中的长方体盒子最多能装( )个这样的小正方体。
A.12 B.18 C.30 D.36
二、填空题
7.在括号里填上合适的单位。
牙膏盒的体积约50( );文具盒的体积约0.35( );
一个热水瓶的容积约2( );一瓶矿泉水的容积是500( )。
8.1.2m3=( )dm3 280cm3=( )dm3 0.6dm3=( )ml
9.如图:每个棱长是1厘米的小正方体堆在墙角处,露在外面的小正方体的面有( )个,露在外面的面积是( )平方厘米,要想补成一个大正方体,至少还需要( )个小正方体。
10.一个正方体的总棱长是216厘米,这个正方体的表面积是( )平方厘米,体积是( )立方厘米。
11.把40颗黄豆放入有水的量杯中(完全浸没),观察水面数据如表,平均每颗黄豆的体积是( )cm3。
放入前 放入后
180mL 204mL
12.一个长方体鱼缸的容积是288L,从里面量这个鱼缸的高正好是0.6m,鱼缸的占地面积是( )m2。
三、判断题
13.棱长是6的正方体体积和表面积一样大。( )
14.一瓶墨水约有60升。( )
15.两个长方体体积相等,表面积也一定相等。( )
16.体积是1dm3的正方体,可以分成10000个棱长是1cm的小正方体。( )
17.把长方体形状的橡皮泥捏成一个正方体,它的形状变了,但体积不变。( )
四、图形计算
18.求出下面图形的表面积和体积。
19.求出下面图形的表面积和体积。
五、解答题
20.一个长方体相交于一个顶点的三条棱的长度之和是21厘米,已知它有4个面是一样大的,其中的一条棱是11厘米,这个长方体的体积是多少?
21.一个长60厘米,宽40厘米,高50厘米的长方形水盆里,放入8个土豆,这样水面就比原来上升了0.4分米,你知道平均每个土豆的体积是多少吗?
22.学校要在操场挖一个长4.5米,宽2.8米,深0.8米的沙坑。这个沙坑的占地面积是多少?现要在沙坑里铺一层厚60厘米的沙土,需要多少立方米的沙土?
23.一块正方体的石料,棱长8分米,这块石料重1843.2千克,每立方分米的石料重多少千克?
24.一个无盖的长方体玻璃鱼缸长4分米,宽2.5分米,高6分米。
(1)要制作这样一个鱼缸,至少需玻璃多少平方分米?
(2)35升水倒入这个鱼缸中,水面距离玻璃鱼缸容器口多少分米?
(3)在这个鱼缸中放了30条小金鱼后,水面上升了0.24厘米。每条小金鱼的体积是多少立方厘米?
参考答案:
1.C
【分析】根据单位之间的换算,大单位换算成小单位要乘它们之间的进率;小单位换算成大单位要除以它们之间的进率即可解答。
【详解】A.180mL=0.18L,10÷0.18≈55.56(元/L)
B.900mL=0.9L,42÷0.9≈46.67(元/L)
C.155÷5=31(元/L)
D.200÷6≈33.33(元/L)
55.56>46.67>33.33>31
因此几种包装的食用油,比较划算。
故答案为:C
【点睛】本题主要考查单位之间的换算,大单位换算成小单位要乘它们之间的进率;小单位换算成大单位要除以它们之间的进率。
2.A
【分析】根据生活经验、数据大小及对单位的认识可知:计量矿泉水瓶的容积用“毫升”作单位;据此解答。
【详解】由分析可得:一个矿泉水瓶的容积大约是550毫升。
故答案为:A
【点睛】联系生活实际,根据计量单位和数据的大小,灵活选择合适的计量单位。
3.C
【分析】根据正方体的体积=棱长×棱长×棱长以及积的变化规律,我们可以得到,一个正方体的棱长扩大到原来的4倍,它的体积扩大到原来的(4×4×4)倍。据此解答。
【详解】4×4×4
=16×4
=64
一个正方体的棱长扩大到原来的4倍,它的体积扩大到原来的64倍。
故答案为:C
【点睛】本题考查了正方体的体积及积的变化规律,解题关键是熟记体积公式。
4.C
【分析】根据题意可知,把这个长方体木料锯成3段,表面积增加了24平方厘米,表面积增加的是4个截面的面积,据此可以求出长方体木料的底面积,再根据长方体的体积公式:V=Sh,把数据代入公式解答。
【详解】1.2米=120厘米
24÷4×120
=6×120
=720(立方厘米)
这根长方体木料的体积是720立方厘米。
故答案为:C
【点睛】此题主要考查长方体的表面积公式、体积公式的灵活运用,关键是熟记公式。
5.D
【分析】根据高减少5cm,就剩下一个正方体可知,这个正方体比原长方体表面积减少的4个面是相同的,根据已知表面积减少了60cm2,60÷4÷5=3cm,求出减少面的宽,也就是剩下的正方体的棱长,然后3+5=8(cm)求出原长方体的高,再计算原长方体的体积即可。
【详解】减少的面的宽(剩下正方体的棱长)
60÷4÷5
=15÷5
=3(cm)
原长方体的高3+5=8(cm)
原长方体体积为:
3×3×8
=9×8
=72(cm3)
原来长方体的体积是72cm3。
故答案为:D
【点睛】根据截去后剩下是正方体,可知减少的部分是宽为3cm的4个面,从而可以分别求出长方体的长、宽、高,进而利用长方体的体积的计算方法即可求解。
6.D
【分析】观察图形可知,沿长方体盒子的长摆了4个小正方体,沿盒子的宽摆了3个小正方体,沿盒子的高摆了3个小正方体,根据长方体体积公式:体积=长×宽×高,求出这个长方体盒子最多能装小正方体的个数。
【详解】4×3×3
=12×3
=36(个)
下图中的长方体盒子最多能装36个小正方体。
故答案为:D
【点睛】分析出长、宽、高各摆了几个小正方体。再运用长方体体积公式进行解答。
7. 立方厘米/cm3 立方分米/dm3 升/L 毫升/mL
【分析】根据生活经验以及数据的大小,选择合适的计量单位,即可解答。
【详解】牙膏盒的体积约50立方厘米;
文具盒的体积约0.35立方分米;
一个热水瓶的容积约2升;
一瓶矿泉水的容积是500毫升。
【点睛】此题考查根据情景选择合适的计量单位,要注意联系生活实际、计量单位和数据的大小,灵活的选择。
8. 1200 0.28 600
【分析】1m3=1000dm3;1dm3=1000cm3;1dm3=1000mL;高度单位换算成低级单位,乘进率;低级单位换算成高级单位,除以进率;据此解答。
【详解】1.2m3=1200dm3
280cm3=0.28dm3
0.6dm3=600mL
【点睛】熟记进率是解答本题的关键。
9. 12 12 21
【分析】根据三视图可知,露在外面的面一共有(4+5+3)个,根据正方形的面积公式,可知一个正方形面的面积是1平方厘米,进而求出露在外面的面有多少平方厘米,要想补成一个大正方体,至少可以补成一个棱长为3厘米的正方体,根据正方体的体积公式,用3×3×3即可求出大正方体的体积,然后除以小正方体的体积,即可求出小正方体的个数,再减去原来小正方体个数,即可求出要想补成一个大正方体,至少还需要多少个小正方体。
【详解】4+5+3=12(个)
1×1×12=12(平方厘米)
(3×3×3)÷(1×1×1)
=27÷1
=27(个)
27-6=21(个)
每个棱长是1厘米的小正方体堆在墙角处,露在外面的小正方体的面有12个,露在外面的面积是12平方厘米,要想补成一个大正方体,至少还需要21个小正方体。
【点睛】解答本题的关键是数出有几个露在外面的面。
10. 1944 5832
【分析】根据正方体的棱长和=棱长×12,用216÷12即可求出正方体的棱长,然后根据正方体的表面积=棱长×棱长×6,正方体的体积=棱长×棱长×棱长,代入数据解答。
【详解】216÷12=18(厘米)
18×18×6
=324×6
=1944(平方厘米)
18×18×18
=324×18
=5832(立方厘米)
这个正方体的表面积是1944平方厘米,体积是5832立方厘米。
【点睛】本题考查了正方体的棱长和公式、表面积公式、体积公式的应用,要熟练掌握公式。
11.0.6
【分析】用放入后的容积减去放入前的容积,求出40粒黄豆的体积,再除以40,即可求出1粒黄豆的体积。
【详解】204-180=24(mL)
24mL=24 cm3
24÷40=0.6(cm3)
均每颗黄豆的体积是0.6cm3。
【点睛】本题考查利用排水法测量不规则物体的体积。
12.0.48
【分析】首先把288L换算成0.288m3,根据长方体的容积(体积)公式:V=Sh,那么S=V÷h,把数据代入公式解答。
【详解】288L=0.288m3
0.288÷0.6=0.48(m2)
鱼缸的占地面积是0.48m2。
【点睛】此题主要考查长方体的容积(体积)公式的灵活运用,关键是熟记公式,注意:容积单位与体积之间的换算。
13.×
【分析】根据正方体的表面积公式:表面积=棱长×棱长×6,体积公式:体积=棱长×棱长×棱长,因为表面积和体积不是同类量,所以它们不能进行比较。
【详解】根据分析可知,表面积和体积不是同类量,所以它们不能进行比较;
棱长是6的正方体体积和表面积无法比较。
原题干说法错误。
故答案为:×
【点睛】本题考查的目的是理解正方体的表面积、体积的意义,明确:表面积和体积不是同类量,所以它们不能进行比较,能进行比较的只有同类量。
14.×
【分析】根据生活经验以及数据的大小,选择合适的计量单位,即可解答。
【详解】一瓶墨水约有60毫升,原题说法错误。
故答案为:×
【点睛】此题考查根据情景选择合适的计量单位,要注意联系生活实际、计量单位和数据的大小,灵活地选择。
15.×
【分析】长方体的表面积=(长×宽+长×高+宽×高)×2,长方体的体积=长×宽×高,据此解答。
【详解】根据题意,若一个长方体的长宽高为6厘米,8厘米,10厘米,另一个长宽高为4厘米,10厘米,12厘米;
体积分别为:
6×8×10
=48×10
=480(立方厘米)
4×10×12
=40×12
=480(立方厘米)
表面积分别为:
(6×8+8×10+6×10)×2
=(48+80+60)×2
=(128+60)×2
=188×2
=376(平方厘米)
(4×10+10×12+4×12)×2
=(40+120+48)×2
=(160+48)×2
=208×2
=416(平方厘米)
两个长方体的体积都是480立方厘米,体积相等,表面积不相等。
故答案为:×
【点睛】本题考查了长方体的体积和表面积公式。
16.×
【分析】根据正方体体积公式:体积=棱长×棱长×棱长,代入数据,求出棱长是1厘米的正方体的体积,再用体积是1dm3正方体的体积÷棱长是1cm正方体的体积,即可求出可以分成多少个棱长是1cm的正方体,再进行判断。
【详解】1dm3=1000cm3
1000÷(1×1×1)
=1000÷(1×1)
=1000÷1
=1000(个)
体积是1dm3的正方体,可以分成1000个棱长是1cm的小正方体。
原题干说法错误。
故答案为:×
【点睛】本题考查立体图形的切拼,以及正方体体积公式的应用,注意单位名数的统一。
17.√
【详解】把一个长方体的橡皮泥捏成正方体,长方体和正方体的体积都是这块橡皮泥的体积,但是六个面的形状发生了变化,表面积变了。比如:将一个长10厘米,宽5厘米、高5厘米的长方体橡皮泥捏成一个正方体,橡皮泥的体积都是10×5×5=250立方厘米,形状由长方体变为正方体,所以把长方体形状的橡皮泥捏成一个正方体,它的形状变了,但体积不变。原说法正确。
故答案为:√
18.表面积:432cm2;体积:540cm3
【分析】根据长方体表面积公式:表面积=(长×宽+长×高+宽×高)×2;长方体体积公式:体积=长×宽×高,代入数据,即可解答。
【详解】(6×6+6×15+6×15)×2
=(36+90+90)×2
=(126+90)×2
=216×2
=432(cm2)
6×6×15
=36×15
=540(cm3)
19.表面积:260cm2;体积:219cm3
【分析】表面积=长是8cm,宽是8cm,高是3cm的长方体的表面积+棱长是3cm的侧面积;根据长方体表面积公式:表面积=(长×宽+长×高+宽×高)×2;正方体侧面积公式:棱长×棱长×4,代入数据,即可解答。
体积=长是8cm,宽是8cm,高是3cm的长方体的体积+棱长是3cm的正方体的体积;根据长方体的体积公式:体积=长×宽×高;正方体体积公式:体积=棱长×棱长×棱长,代入数据,即可解答。
【详解】表面积:(8×8+8×3+8×3)×2+3×3×4
=(64+24+24)×2+9×4
=(88+24)×2+36
=112×2+36
=224+36
=260(cm2)
体积:8×8×3+3×3×3
=64×3+9×3
=192+27
=219(cm3)
20.275立方厘米
【分析】一个长方体相交与一个顶点的三条棱的长度之和是21厘米,则长+宽+高=21厘米,已知它有4个面是一样大的,则长、宽、高中有2个棱是相等的,因为11+11=22,所以不能有2个11厘米,所以另外两个棱相等;用21-11求出另外两条棱的和,再除以2,求出一条棱的长度,再根据长方体体积公式:体积=长×宽×高,代入数据,即可解答。
【详解】(21-11)÷2
=10÷2
=5(厘米)
11×5×5
=55×5
=275(立方厘米)
答:这个长方体的体积是275立方厘米。
【点睛】本体考查长方体特征以及长方体体积公式的应用,关键是熟记公式。
21.1200立方厘米
【分析】根据不规则物体的体积公式:容器的底面积×水面变化的高度=不规则物体的体积,再除以8即可求出平均每个土豆的体积。
【详解】0.4分米=4厘米
60×40×4=9600(立方厘米)
9600÷8=1200(立方厘米)
答:平均每个土豆的体积是1200立方厘米。
【点睛】本题主要考查不规则物体体积公式,熟练掌握它的公式并灵活运用。
22.12.6平方米;7.56立方米
【分析】占地面积就是底面面积;用底面积乘沙土厚度,注意单位要统一;根据长方体的容积(体积)公式:V=abh,把数据代入公式解答。
【详解】4.5×2.8=12.6(平方米)
60厘米=0.6米
12.6×0.6=7.56(立方米)
答:这个沙坑的占地面积是12.6平方米,需要7.56立方米的沙土。
【点睛】本题主要考查长方体体积的计算。
23.3.6千克
【分析】根据正方体的体积=棱长×棱长×棱长,用8×8×8即可求出石料的体积,然后用1843.2千克除以石料的体积即可求出每立方分米的石料重多少千克。
【详解】1843.2÷(8×8×8)
=1843.2÷512
=3.6(千克)
答:每立方分米的石料重3.6千克。
【点睛】本题主要考查了正方体体积公式的灵活应用。
24.(1)88平方分米;(2)2.5分米;(3)8立方厘米
【分析】(1)无盖的长方体表面积只有5个面的面积,根据无盖的长方体面积=长×宽+长×高×2+宽×高×2,用4×2.5+4×6×2+2.5×6×2即可求出无盖的长方体鱼缸的表面积。
(2)35升=35立方分米,根据长方体的体积=长×宽×高,用35÷4÷2.5即可求出水的高度,然后用鱼缸的高度减去水的高度,即可求出水面距离玻璃鱼缸容器口多少分米;
(3)0.24厘米=0.024分米,根据物体的体积=上升部分水的体积,物体的体积=长×宽×上升部分的高度,用4×2.5×0.024即可求出30条金鱼的体积。然后把结果化为立方厘米,再根据除法的意义,用鱼的总体积除以30,即可求出每条鱼的体积,据此解答。
【详解】(1)4×2.5+4×6×2+2.5×6×2
=10+48+30
=88(平方分米)
答:要制作这样一个鱼缸,至少需玻璃88平方分米。
(2)35升=35立方分米
35÷4÷2.5=3.5(分米)
6-3.5=2.5(分米)
答:水面距离玻璃鱼缸容器口2.5分米。
(3)0.24厘米=0.024分米
4×2.5×0.024=0.24(立方分米)
0.24立方分米=240立方厘米
240÷30=8(立方厘米)
答:每条小金鱼的体积是8立方厘米。
【点睛】本题主要考查了长方体表面积公式、体积公式的灵活应用,要注意统一单位。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
