三角形中的热点问题举例[下学期]

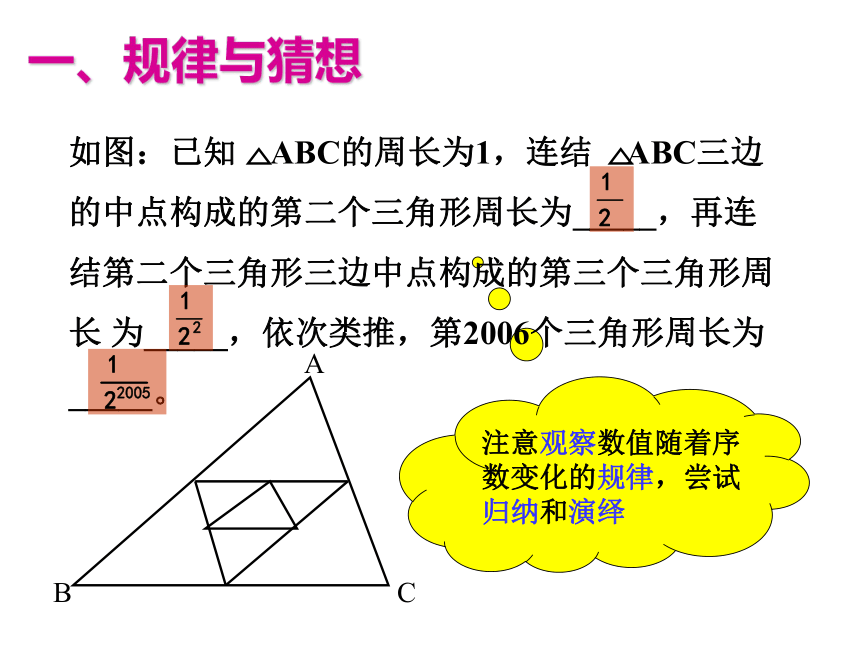
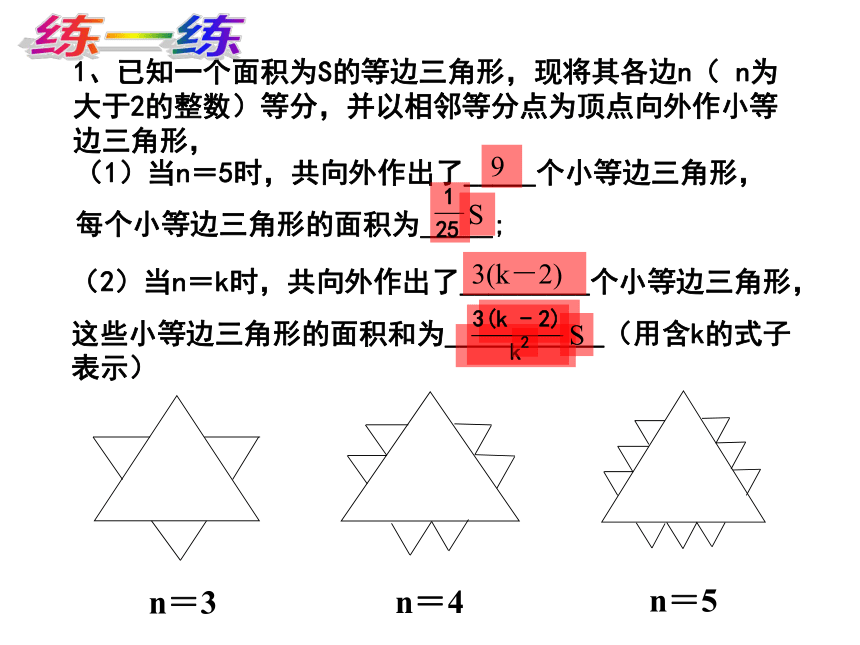
课件14张PPT。引导者：吴菊敏三角形中的热点问题举例观察下列图形的排列规律（其中 是三角形， 是正方形， 圆）， …，若第一个图形是正方形，则第2006个图形是_____（填图形名称）。大胆猜想，让思维活起来！热身运动一、规律与猜想200521、已知一个面积为S的等边三角形，现将其各边n（ n为大于2的整数）等分，并以相邻等分点为顶点向外作小等边三角形，（1）当n＝5时，共向外作出了_____个小等边三角形，
每个小等边三角形的面积为_____;（2）当n＝k时，共向外作出了_________个小等边三角形，
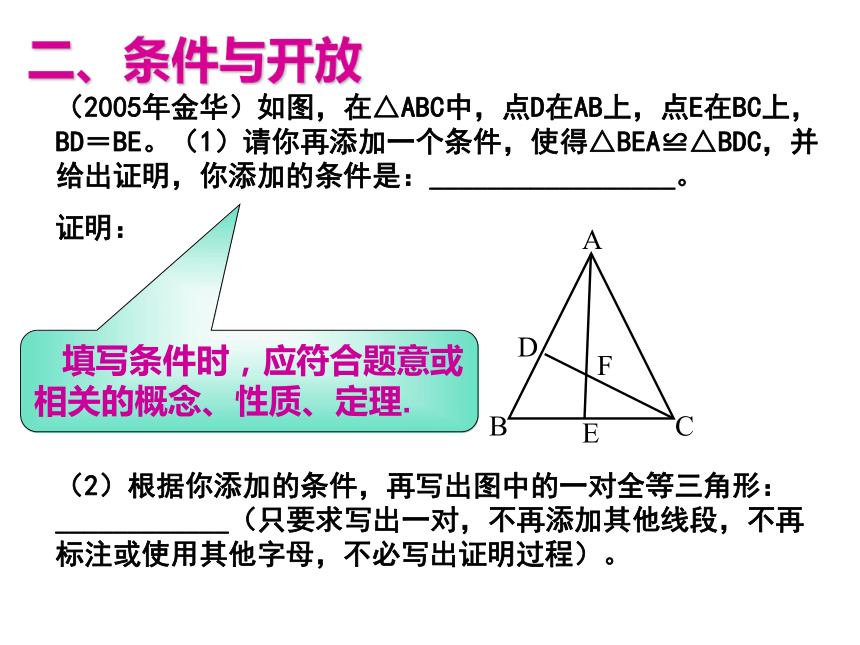
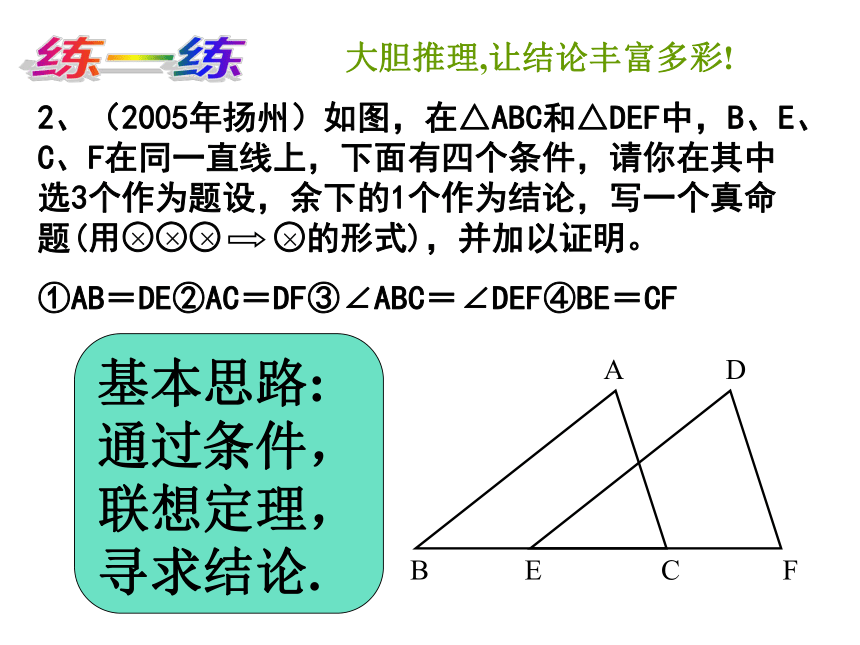
这些小等边三角形的面积和为___________（用含k的式子表示）9S3(k－2)练一练二、条件与开放 填写条件时，应符合题意或相关的概念、性质、定理.练一练大胆推理,让结论丰富多彩!基本思路:通过条件，联想定理，寻求结论.定底定高适当变形直击要点不重不漏(2004年重庆)在如图的方格纸中，每个小方格都是边长为1的正方形，点A、B是方格纸中的两个格点（即正方形的顶点），在这个5×5的方格纸中，请画出一个面积为2个平方单位的格点△ABC.
(你知道这样的点有几个吗？）三、网格与操作●●●●●3、（2005年无锡）练一练如图,在Rt△ABC中 ,∠C＝90°, AC＝6,BC＝8,点E在AC上从A点向C点以2cm每秒的速度移动(运动到C点停止),点F在AB上从B点向A点以1cm每秒的速度移动(运动到A点停止).(1)当运动时间t为几秒时,线段EF平分Rt△ABC的周长? (根据2005年宁夏课改实验区试题改编)四、运动与探索10－t2t＋(10－t)＝12t＝2(2)你能写出△AEF的面积S关于时间t的函数关系式吗?
若能，请求出t的取值范围；10－t如图,在Rt△ABC中 ,∠C＝90°, AC＝6,BC＝8,点E在AC上从A点向C点以2cm每秒的速度移动(运动到C点停止),点F在AB上从B点向A点以1cm每秒的速度移动(运动到A点停止).(0＜t≤3)(3)是否存在时刻t,使得△AEF的面积S达到最大值?若存在,求
出S的值;若不存在,说明理由.10－t如图,在Rt△ABC中 ,∠C＝90°, AC＝6,BC＝8,点E在AC上从A点向C点以2cm每秒的速度移动(运动到C点停止),点F在AB上从B点向A点以1cm每秒的速度移动(运动到A点停止).(0＜t≤3)S＝－ t2＋8t＝－ (t－5)2 ＋20
当t ＝3时,S最大＝使我感触最深的是……
我还感到疑惑的是……回味无穷课后作业大胆尝试，你一定行！脚踏实地
迈向成功结束寄语