探索三角形全等的条件SAS[下学期]

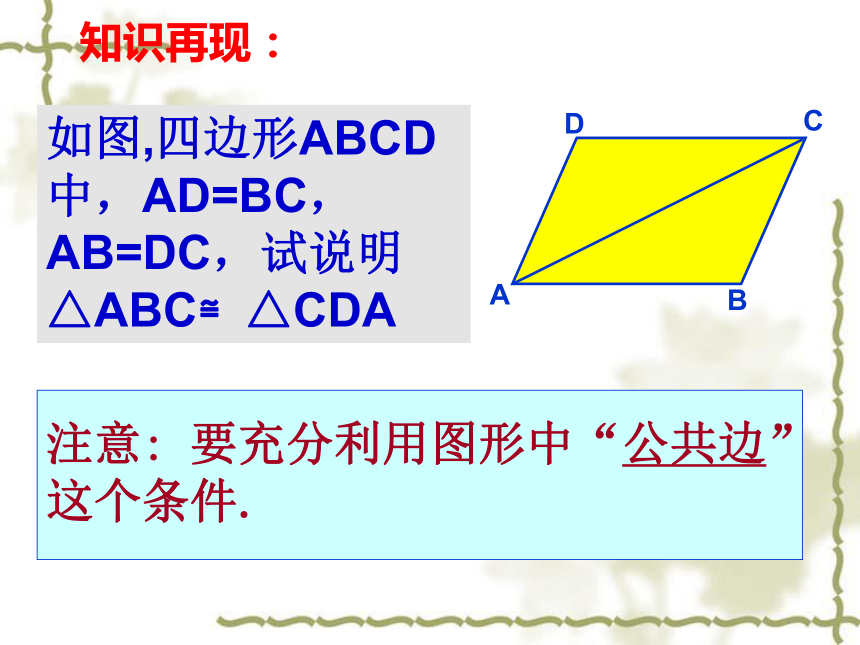
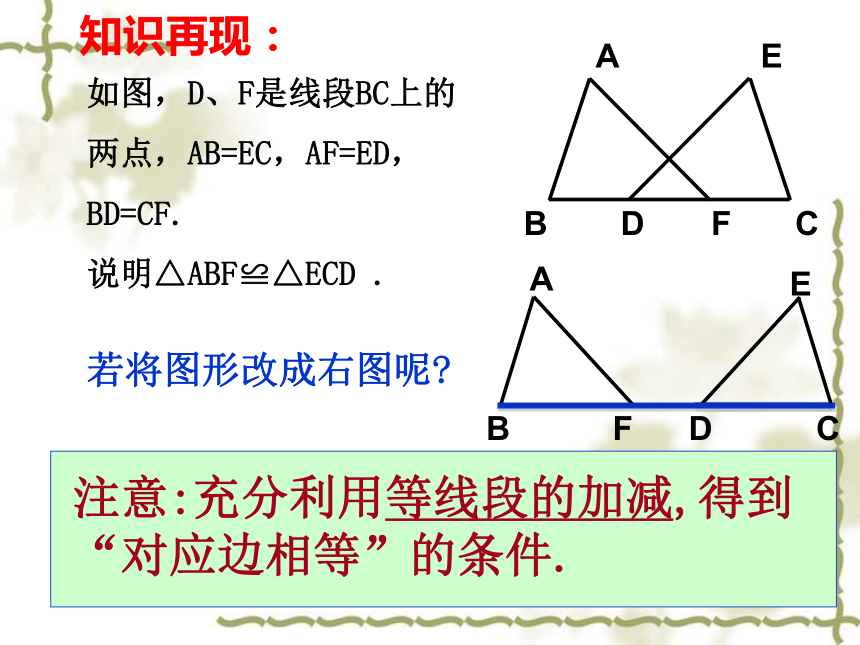
课件19张PPT。11.3探索三角形全等的条件（2）—SAS（边角边）你还记得吗？什么叫全等三角形？两个能完全重合的三角形叫做全等三角形。全等三角形的对应边、对应角有什么重要性质？全等三角形的对应边相等，对应角相等。三边对应相等的两个三角形全等. (SSS)三角形全等的判定方法?知识再现：如图,四边形ABCD中，AD=BC，AB=DC，试说明△ABC≌△CDA注意: 要充分利用图形中“公共边”这个条件.如图，D、F是线段BC上的两点，AB=EC，AF=ED，BD=CF.
说明△ABF≌△ECD . B D F C
若将图形改成右图呢?知识再现：注意:充分利用等线段的加减,得到“对应边相等”的条件.知识再现：探索三角形全等的条件:一个条件,
2. 两个条件, 三个条件:
⑴ 三个角对应相等
⑵　三条边对应相等不能保证三角形全等.
能判定三角形全等.⑶ 两边一角对应相等
⑷ 两角一边对应相等不能保证三角形全等.
不能保证三角形全等.
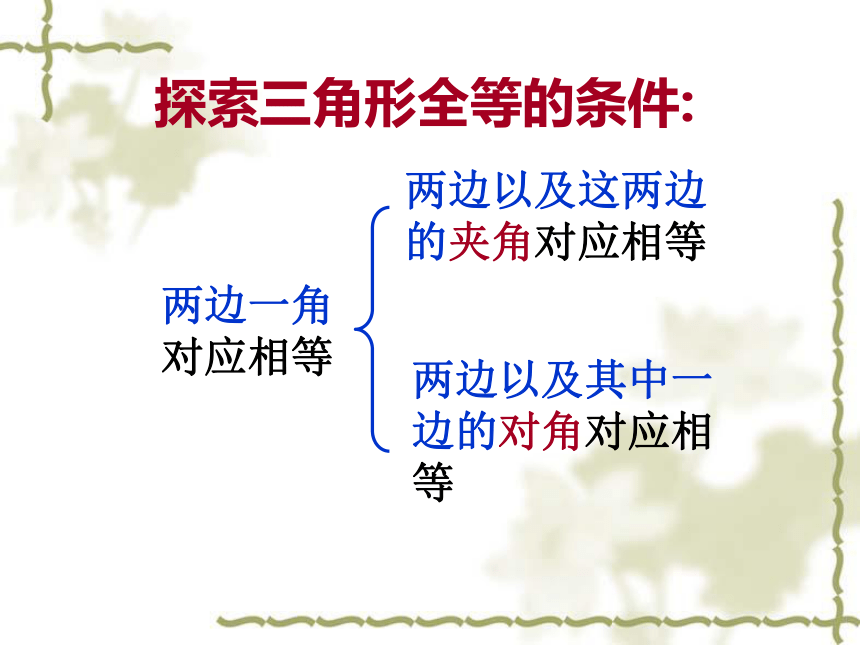
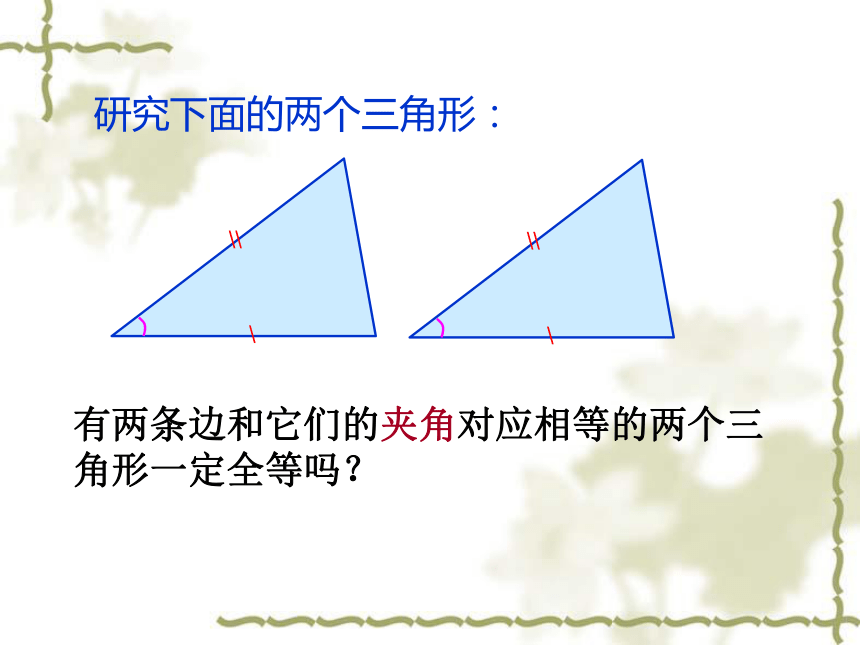
探索三角形全等的条件:两边一角对应相等两边以及这两边的夹角对应相等两边以及其中一边的对角对应相等有两条边和它们的夹角对应相等的两个三角形一定全等吗？研究下面的两个三角形：大家一起做下面的实验：1、画∠MAN=45°；
2、在AM上截取AB=3cm；在AN上截取AC=2cm；
3、连接BC。
剪下所得的△ABC，与周围同学所剪的比较一下，它们全等吗？BC′探究一:两边和它们的夹角对应相等的两个三角形全等，简写成“边角边”或“SAS”在△ABC和△ DEF中，
AB=DE
∠B=∠E
BC=EF
∴ △ABC≌△DEF (SAS)

条件:两个三角形两边以及这两边的夹角对应相等结论:这两个三角形全等条件: AB=DE,
∠B=∠E, BC=EF结论: △ABC≌△DEF P141练一练1: 在下列三角形中,哪两个三角形全等?
⑴⑵⑶⑷⑸⑹解:全等的三角形有:⑴和⑷, ⑶和⑸.
两边以及其中一边的对角对应相等的两个三角形全等吗？探究二: 以2.5cm，3.5cm为三角形的两边，长度为2.5cm的边所对的角为40° ，情况又怎样？动手画一画，你发现了什么？ABCDEF2.5cm3.5cm40°40°3.5cm2.5cm结论：两边及其中一边所对的角对应相等，两个三角形不一定全等.先画一个角40°的角,然后在其中一边上取3.5厘米,最后画40°的角所对的边2.5厘米.已知：如图， AB=CB ，∠ABD= ∠CBD
△ABD 和△CBD 全等吗？
分析:△ ABD ≌△ CBDAB=CB (已知)∠ABD=∠CBD (已知)？ABCD 现在例1的已知条件不改变,而问题改变成:
问:AD=CD，BD平分∠ADC吗？ 已知：如图,AB=CB,∠ABD=∠CBD .
问: AD=CD， BD 平分∠ ADC 吗？归纳：判定两条线段相等或两个角相等可以通过从它们所在的两个三角形全等而得到。1. 如图,AC与BD相交于点O，已知OA=OC，OB=OD，说明△AOB≌△COD的理由。注意: 要充分利用图形中“对顶角相等”这个条件.练一练：2. 如图，AC=BD，∠CAB= ∠DBA，你能判断BC=AD吗？说明理由。3、如图：AB=AC，AD=AE，△ABE和△ACD全等吗？请说明理由。练一练：注意: 要充分利用图形中“公共角”这个条件.你还能得到哪些相等的线段?说明理由.说一说　　这节课你学到了什么？两边和它们的夹角对应相等的两个三角形全等，简写成“边角边”或“SAS”两边以及其中一边的对角对应相等的两个三角形不一定全等.注意:要充分利用图形中“对顶角相等,公共角”这些条件.判定两条线段相等或两个角相等可以通过从它们所在的两个三角形全等而得到。P151~152：1、3、4
评价手册:79~81第1课时作业：