探索规律[下学期]
图片预览


文档简介
二、填空题
14、(2005深圳市课改实验区)已知:,,,……,若(a、b都是正整数),则a+b的最小值是___19____。
1 8 2005甘肃省课改实验区.用黑白两种颜色的正六边形地板砖按图6所示的规律,拼成如下若干地板图案:则第n个图案中,白色的地板砖有 4n+2 块.
16. 2005资阳市课改实验区已知n(n≥2)个点P1,P2,P3,…,Pn在同一平面内,且其中没有任何三点在同一直线上. 设Sn表示过这n个点中的任意2个点所作的所有直线的条数,显然,S2=1,S3=3,S4=6,S5=10,…,由此推断,Sn=______________.
16.(2005江苏省淮安市金湖实验区)已知一列数:1,―2,3,―4,5,―6,7,… 将这列数排成下列形式:
第1行 1
第2行 -2 3
第3行 -4 5 -6
第4行 7 -8 9 -10
第5行 11 -12 13 -14 15
… …
按照上述规律排下去,那么第10行从左边数第5个数等于 -50 .
1、(2005福建漳州)14.观察分析下列数据,按规律填空:,2,,2,,…, (第n个数)。
15. 扑克牌游戏
小明背对小亮,让小亮按下列四个步骤操作:
第一步 分发左、中、右三堆牌,每堆牌不少于两张,
且各堆牌现有的张数相同;
第二步 从左边一堆拿出两张,放入中间一堆;
第三步 从右边一堆拿出一张,放入中间一堆;
第四步 左边一堆有几张牌,就从中间一堆拿几张牌放入左边一堆.
这时,小明准确说出了中间一堆牌现有的张数.你认为中间一堆牌现有的张数是 5 .
16.(2005山东枣庄课改实验区)100个数排成一行,其中任意三个相邻数中,中间一个数都等于它前后两个数的和, 如果这100个数的前两个数依次为1,0,那么这100个数中“0”的个数为 __ 33 _个.
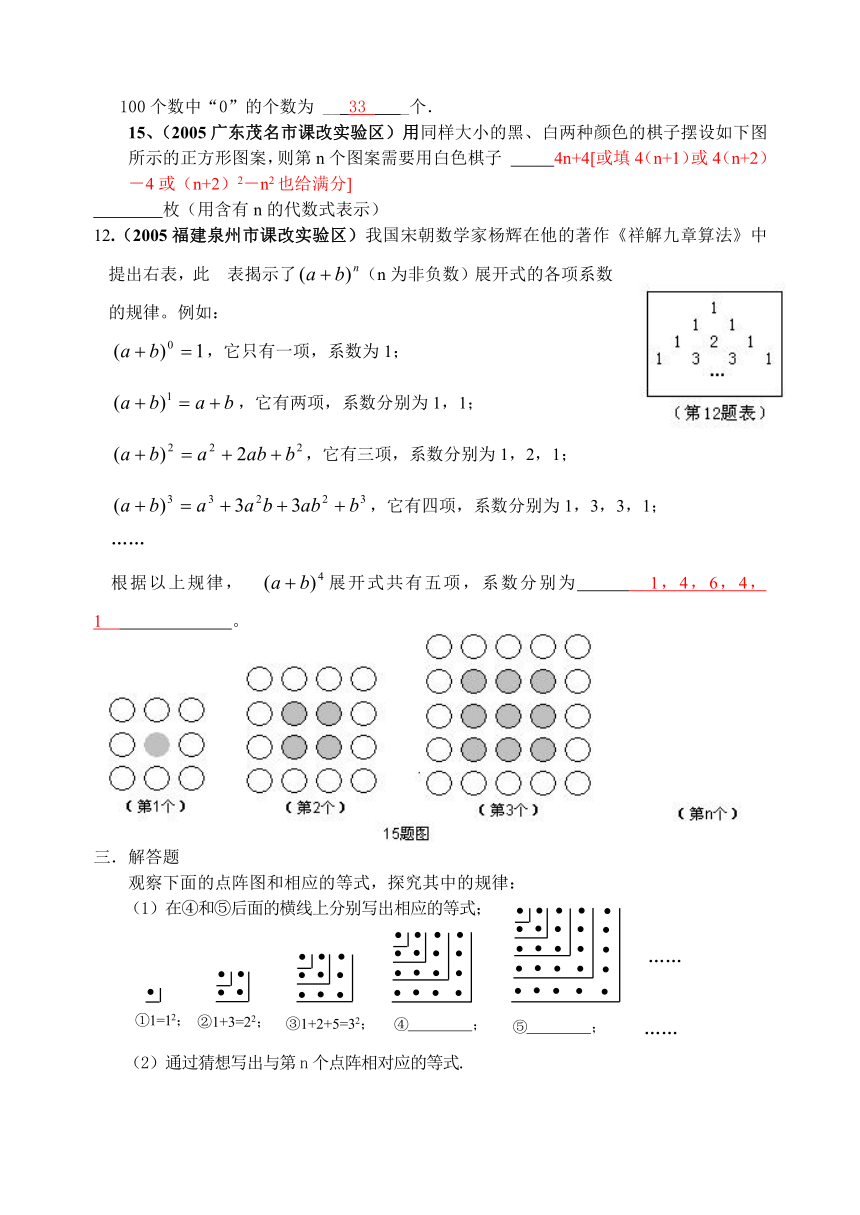
15、(2005广东茂名市课改实验区)用同样大小的黑、白两种颜色的棋子摆设如下图所示的正方形图案,则第n个图案需要用白色棋子 4n+4[或填4(n+1)或4(n+2)-4或(n+2)2-n2也给满分]
枚(用含有n的代数式表示)
12.(2005福建泉州市课改实验区)我国宋朝数学家杨辉在他的著作《祥解九章算法》中提出右表,此 表揭示了(n为非负数)展开式的各项系数的规律。例如:
,它只有一项,系数为1;
,它有两项,系数分别为1,1;
,它有三项,系数分别为1,2,1;
,它有四项,系数分别为1,3,3,1;
……
根据以上规律,展开式共有五项,系数分别为 1,4,6,4,1 。
三.解答题
观察下面的点阵图和相应的等式,探究其中的规律:
(1)在④和⑤后面的横线上分别写出相应的等式;
(2)通过猜想写出与第n个点阵相对应的等式.
18. 答:(1)④1+3+5+7=42;⑤1+3+5+7+9=52. ……………………………………4分
(2)1+3+5+…+(2n-1)=n2 ………………………………………………6分
16、(2005山东济南课改实验区)把数字按如图所示排列起来,从上开始,依次为第一行、第二行、第三行、……,中间用虚线围的一列,从上至下依次为1、5、13、25、……,则第10个数为________。
操作与探究
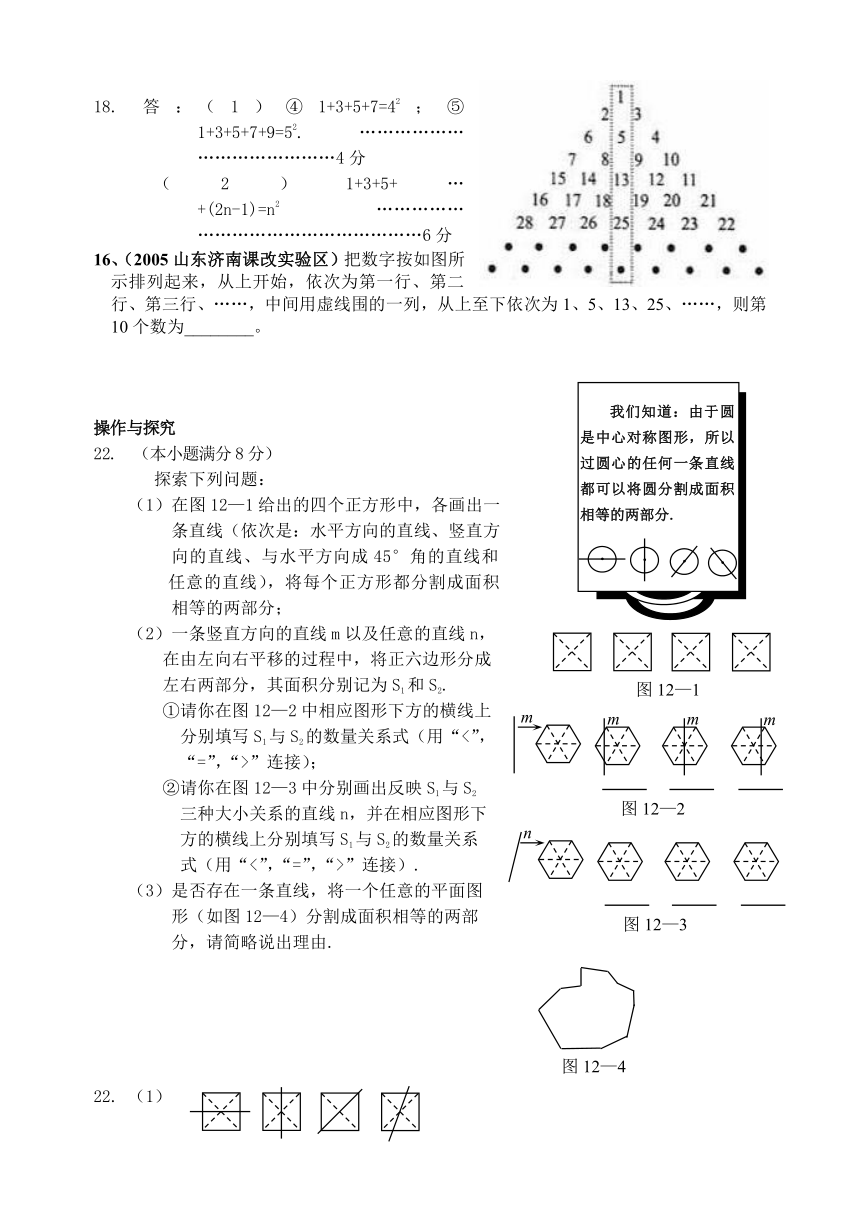
22. (本小题满分8分)
探索下列问题:
(1)在图12—1给出的四个正方形中,各画出一
条直线(依次是:水平方向的直线、竖直方
向的直线、与水平方向成45°角的直线和
任意的直线),将每个正方形都分割成面积
相等的两部分;
(2)一条竖直方向的直线m以及任意的直线n,
在由左向右平移的过程中,将正六边形分成
左右两部分,其面积分别记为S1和S2.
①请你在图12—2中相应图形下方的横线上
分别填写S1与S2的数量关系式(用“<”,
“=”,“>”连接);
②请你在图12—3中分别画出反映S1与S2
三种大小关系的直线n,并在相应图形下
方的横线上分别填写S1与S2的数量关系
式(用“<”,“=”,“>”连接).
(3)是否存在一条直线,将一个任意的平面图
形(如图12—4)分割成面积相等的两部
分,请简略说出理由.
22. (1)
(2)① ……………………………………………………2分
②
………………………………………………………6分
(3)存在.
对于任意一条直线l ,在直线l从平面图形的一侧向另一侧平移的过程中,当图形被直线l分割后,设直线l两侧图形的面积分别为S1,S2.两侧图形的面积由S1S2)的情形,逐渐变为S1>S2(或S125. (本小题满分12分)
如图15—1和15—2,在20×20的等距网格(每格的宽和高均是1个单位长)中,
Rt△ABC从点A与点M重合的位置开始,以每秒1个单位长的速
度先向下平移,当BC边与网的底部重合时,继续同样的速度向右
平移,当点C与点P重合时,Rt△ABC停止移动.设运动时间
为x秒,△QAC的面积为y.
(1)如图15—1,当Rt△ABC向下平移到Rt△A1B1C1的位置时,
请你在网格中画出Rt△A1B1C1关于直线QN成轴对称的图形;
(2)如图15—2,在Rt△ABC向下平移的过程中,请你求出y与
x的函数关系式,并说明当x分别取何值时,y取得最大值和
最小值?最大值和最小值分别是多少?
(3)在Rt△ABC向右平移的过程中,请你说明当x取何值时,y
取得最大值和最小值?最大值和最值分别是多少?为什么?
(说明:在(3)中,将视你解答方法的创新程度,给予1~4分的加分)
25. 解:(1)如图1,△A2B2C2是△A1B1C1关于直线QN成轴对称的图形. …………2分
(2)当△ABC以每秒1个单位长的速度向下平移x秒时(如图2),则有:
MA=x,MB=x+4,MQ=20,
y=S梯形QMBC-S△AMQ-S△ABC
=
=2x+40(0≤x≤16). ……………………………………………………6分
由一次函数的性质可知:
当x=0时,y取得最小值,且y最小=40;
当x=16时,y取得最大值,且y最大=2×16+40=72.………………………………8分
(3)解法一:
当△ABC继续以每秒1个单位长的速度向右平移时,此时16≤x≤32,PB=20-(x-16)=36-x,PC=PB-4=32-x,
∴y=S梯形BAQP-S△CPQ-S△ABC
=-2x+104(16≤x≤32). ………………………………………………10分
由一次函数的性质可知:
当x=32时,y取得最小值,且y最小=-2×32+104=40;
当x=16时,y取得最大值,且y最大=-2×16+104=72.……………………12分
解法二:
在△ABC自左向右平移的过程中,△QAC在每一时刻的位置都对应着(2)中△QAC某一时刻的位置.使得这样的两个三角形关于直线QN成轴对称.
因此,根据轴对称的性质,只需考察△ABC在自上至下平移过程中△QAC面积的变化情况,便可以知道△ABC在自左向右平移过程中△QAC面积的变化情况.
当x=16时,y取得最大值,且y最大=72;
当x=32时,y取得最小值,且y最小=40.……………………12分(再加2分)
说明:(1)本题解法较多,对于其他正确解法,请参照评分标准按步骤给分;
(2)对于(3),如果学生按照解法一的方法求解,不加分;如果按照解法二利用图形变换的方法说明,可考虑加1~4分.
21.(2005广东省佛山市课改实验区)如图,在水平桌面上的两个“E”,当点在一条直线上时,在点O处用①号“E”测得的视力与用②号“E”测得的视力效果相同.
(1)图中满足怎样的关系式?
(2)若①号“E”的测量距离,要使得测得的视力相同,则②号“E”的测量距离应为多少?
23(2005年恩施自治州课改实验区).下图的数阵是由全体奇数排成
(1)图中平行四边形框内的九个数之和与中间的数有什么关系?
(2)在数阵图中任意作一类似(1)中的平行四边形框,这九个数之和还有这种规律吗?请说出理由;
(3)这九个数之和能等于1998吗?2005,1017呢?若能,请写出这九个数中最小的一个,若不能,请说出理由。
23.(1) 平行四边形框内的九个数之和是中间的数的9倍 ( 2分)
(2) 任意作一类似(1)中的平行四边形框,规律仍然成立.
不仿设框中间的数为n,这九个数按大小顺序依次为:
(n-18),(n-16),(n-14),(n-2),n,(n+2),(n+14),(n+16),(n+18).
显然,其和为9n ( 6分)
(3) 这九个数之和不能为1998
若和为1998,则9n=1998,n=222,是偶数,
显然不在数阵中. ( 7分)
这九个数之和也不能为2005
因为2005不能被9整除; (8分)
观察表中规律,框中间数不能在前面两列、也不能在后面两列,各列与18相除余数分别为1,3,5,7,9,11,13,15,17.
若和为1017,则中间数可能为113,而除以18的余数为3,
满足条件,其最小的数为95. ( 10分)
19.(2005河南课改实验区)在数学活动中,小明为了求的值(结果用n表示),设计如图7-1所示的几何图形。
(1)请你利用这个几何图形求
的值为__________。
(2)请你利用图7-2,再设计一个能求
的值的几何图形。
19.解:(1)。………………………………………………………………………4分
(2)如图1-1或如图1-2或如图1-3或如图1-4等,图形正确。……10分
归纳与猜想
18、(2005河北课改实验区)(本小题满分7分)
观察右面的图形(每个正方形的边长均为1)和相应等式,控究其中的规律:
①
②
③
④
……
⑴写出第五个等式,并在右边给出的五个正方形上画出与之对应的图示:
⑵猜想并写出与第n个图形相对应的等式。
18、解:⑴ ……………………………………………………2分
…………………………………………4分
⑵……………………………………………………7分
21. (2005安徽课改实验区)下图中, 图(1)是一个扇形AOB,将其作如下划分:
第一次划分: 如图(2)所示,以OA的一半OA1为半径画弧,再作∠AOB的平分线, 得到扇形的总数为6个, 分别为: 扇形AOB、扇形AOC、扇形COB、扇形A1OB1、扇形A1OC1、扇形C1OB1;
第二次划分: 如图(3)所示, 在扇形C1OB1中, 按上述划分方式继续划分, 可以得到扇形的总数为11个;
第三次划分: 如图(4)所示;
……
依次划分下去.
图(1) 图(2)第一次划分 图(3)第二次划分 图(4)第三次划分
(1) 根据题意, 完成下表:
划分次数 扇形总个数
1 6
2 11
3
4
… …
n
(2) 根据上表, 请你判断按上述划分方式, 能否得到扇形的总数为2005个 为什么
【解】
六、探索规律(本题满分12分)
划分次数 扇形总个数
1 6
2 11
3 16
4 21
21.(1)
9分
(2)不能够得到2005个扇形,因为满足的正整数不存在. 12分
④ ;
③1+2+5=32;
②1+3=22;
①1=12;
……
……
⑤ ;
我们知道:由于圆是中心对称图形,所以过圆心的任何一条直线都可以将圆分割成面积相等的两部分.
图12—1
m
m
m
m
图12—2
n
图12—3
图12—4
O
N
P
Q
M
C
C1
B1
A1
A
B
图15—1
O
N
P
Q
M
C
A
B
图15—2
你能行,加
油呀!
S1S1=S2
S1>S2
S1S1=S2
S1>S2
O
N
P
Q
M
C1
C2
B1
A1
A2
B2
图1
O
N
P
Q
M
C
A
B
C
A
B
图2
图中有规律哟!
图7-2
图7-1
14、(2005深圳市课改实验区)已知:,,,……,若(a、b都是正整数),则a+b的最小值是___19____。
1 8 2005甘肃省课改实验区.用黑白两种颜色的正六边形地板砖按图6所示的规律,拼成如下若干地板图案:则第n个图案中,白色的地板砖有 4n+2 块.
16. 2005资阳市课改实验区已知n(n≥2)个点P1,P2,P3,…,Pn在同一平面内,且其中没有任何三点在同一直线上. 设Sn表示过这n个点中的任意2个点所作的所有直线的条数,显然,S2=1,S3=3,S4=6,S5=10,…,由此推断,Sn=______________.
16.(2005江苏省淮安市金湖实验区)已知一列数:1,―2,3,―4,5,―6,7,… 将这列数排成下列形式:
第1行 1
第2行 -2 3
第3行 -4 5 -6
第4行 7 -8 9 -10
第5行 11 -12 13 -14 15
… …
按照上述规律排下去,那么第10行从左边数第5个数等于 -50 .
1、(2005福建漳州)14.观察分析下列数据,按规律填空:,2,,2,,…, (第n个数)。
15. 扑克牌游戏
小明背对小亮,让小亮按下列四个步骤操作:
第一步 分发左、中、右三堆牌,每堆牌不少于两张,
且各堆牌现有的张数相同;
第二步 从左边一堆拿出两张,放入中间一堆;
第三步 从右边一堆拿出一张,放入中间一堆;
第四步 左边一堆有几张牌,就从中间一堆拿几张牌放入左边一堆.
这时,小明准确说出了中间一堆牌现有的张数.你认为中间一堆牌现有的张数是 5 .
16.(2005山东枣庄课改实验区)100个数排成一行,其中任意三个相邻数中,中间一个数都等于它前后两个数的和, 如果这100个数的前两个数依次为1,0,那么这100个数中“0”的个数为 __ 33 _个.
15、(2005广东茂名市课改实验区)用同样大小的黑、白两种颜色的棋子摆设如下图所示的正方形图案,则第n个图案需要用白色棋子 4n+4[或填4(n+1)或4(n+2)-4或(n+2)2-n2也给满分]
枚(用含有n的代数式表示)
12.(2005福建泉州市课改实验区)我国宋朝数学家杨辉在他的著作《祥解九章算法》中提出右表,此 表揭示了(n为非负数)展开式的各项系数的规律。例如:
,它只有一项,系数为1;
,它有两项,系数分别为1,1;
,它有三项,系数分别为1,2,1;
,它有四项,系数分别为1,3,3,1;
……
根据以上规律,展开式共有五项,系数分别为 1,4,6,4,1 。
三.解答题
观察下面的点阵图和相应的等式,探究其中的规律:
(1)在④和⑤后面的横线上分别写出相应的等式;
(2)通过猜想写出与第n个点阵相对应的等式.
18. 答:(1)④1+3+5+7=42;⑤1+3+5+7+9=52. ……………………………………4分
(2)1+3+5+…+(2n-1)=n2 ………………………………………………6分
16、(2005山东济南课改实验区)把数字按如图所示排列起来,从上开始,依次为第一行、第二行、第三行、……,中间用虚线围的一列,从上至下依次为1、5、13、25、……,则第10个数为________。
操作与探究
22. (本小题满分8分)
探索下列问题:
(1)在图12—1给出的四个正方形中,各画出一
条直线(依次是:水平方向的直线、竖直方
向的直线、与水平方向成45°角的直线和
任意的直线),将每个正方形都分割成面积
相等的两部分;
(2)一条竖直方向的直线m以及任意的直线n,
在由左向右平移的过程中,将正六边形分成
左右两部分,其面积分别记为S1和S2.
①请你在图12—2中相应图形下方的横线上
分别填写S1与S2的数量关系式(用“<”,
“=”,“>”连接);
②请你在图12—3中分别画出反映S1与S2
三种大小关系的直线n,并在相应图形下
方的横线上分别填写S1与S2的数量关系
式(用“<”,“=”,“>”连接).
(3)是否存在一条直线,将一个任意的平面图
形(如图12—4)分割成面积相等的两部
分,请简略说出理由.
22. (1)
(2)① ……………………………………………………2分
②
………………………………………………………6分
(3)存在.
对于任意一条直线l ,在直线l从平面图形的一侧向另一侧平移的过程中,当图形被直线l分割后,设直线l两侧图形的面积分别为S1,S2.两侧图形的面积由S1
如图15—1和15—2,在20×20的等距网格(每格的宽和高均是1个单位长)中,
Rt△ABC从点A与点M重合的位置开始,以每秒1个单位长的速
度先向下平移,当BC边与网的底部重合时,继续同样的速度向右
平移,当点C与点P重合时,Rt△ABC停止移动.设运动时间
为x秒,△QAC的面积为y.
(1)如图15—1,当Rt△ABC向下平移到Rt△A1B1C1的位置时,
请你在网格中画出Rt△A1B1C1关于直线QN成轴对称的图形;
(2)如图15—2,在Rt△ABC向下平移的过程中,请你求出y与
x的函数关系式,并说明当x分别取何值时,y取得最大值和
最小值?最大值和最小值分别是多少?
(3)在Rt△ABC向右平移的过程中,请你说明当x取何值时,y
取得最大值和最小值?最大值和最值分别是多少?为什么?
(说明:在(3)中,将视你解答方法的创新程度,给予1~4分的加分)
25. 解:(1)如图1,△A2B2C2是△A1B1C1关于直线QN成轴对称的图形. …………2分
(2)当△ABC以每秒1个单位长的速度向下平移x秒时(如图2),则有:
MA=x,MB=x+4,MQ=20,
y=S梯形QMBC-S△AMQ-S△ABC
=
=2x+40(0≤x≤16). ……………………………………………………6分
由一次函数的性质可知:
当x=0时,y取得最小值,且y最小=40;
当x=16时,y取得最大值,且y最大=2×16+40=72.………………………………8分
(3)解法一:
当△ABC继续以每秒1个单位长的速度向右平移时,此时16≤x≤32,PB=20-(x-16)=36-x,PC=PB-4=32-x,
∴y=S梯形BAQP-S△CPQ-S△ABC
=-2x+104(16≤x≤32). ………………………………………………10分
由一次函数的性质可知:
当x=32时,y取得最小值,且y最小=-2×32+104=40;
当x=16时,y取得最大值,且y最大=-2×16+104=72.……………………12分
解法二:
在△ABC自左向右平移的过程中,△QAC在每一时刻的位置都对应着(2)中△QAC某一时刻的位置.使得这样的两个三角形关于直线QN成轴对称.
因此,根据轴对称的性质,只需考察△ABC在自上至下平移过程中△QAC面积的变化情况,便可以知道△ABC在自左向右平移过程中△QAC面积的变化情况.
当x=16时,y取得最大值,且y最大=72;
当x=32时,y取得最小值,且y最小=40.……………………12分(再加2分)
说明:(1)本题解法较多,对于其他正确解法,请参照评分标准按步骤给分;
(2)对于(3),如果学生按照解法一的方法求解,不加分;如果按照解法二利用图形变换的方法说明,可考虑加1~4分.
21.(2005广东省佛山市课改实验区)如图,在水平桌面上的两个“E”,当点在一条直线上时,在点O处用①号“E”测得的视力与用②号“E”测得的视力效果相同.
(1)图中满足怎样的关系式?
(2)若①号“E”的测量距离,要使得测得的视力相同,则②号“E”的测量距离应为多少?
23(2005年恩施自治州课改实验区).下图的数阵是由全体奇数排成
(1)图中平行四边形框内的九个数之和与中间的数有什么关系?
(2)在数阵图中任意作一类似(1)中的平行四边形框,这九个数之和还有这种规律吗?请说出理由;
(3)这九个数之和能等于1998吗?2005,1017呢?若能,请写出这九个数中最小的一个,若不能,请说出理由。
23.(1) 平行四边形框内的九个数之和是中间的数的9倍 ( 2分)
(2) 任意作一类似(1)中的平行四边形框,规律仍然成立.
不仿设框中间的数为n,这九个数按大小顺序依次为:
(n-18),(n-16),(n-14),(n-2),n,(n+2),(n+14),(n+16),(n+18).
显然,其和为9n ( 6分)
(3) 这九个数之和不能为1998
若和为1998,则9n=1998,n=222,是偶数,
显然不在数阵中. ( 7分)
这九个数之和也不能为2005
因为2005不能被9整除; (8分)
观察表中规律,框中间数不能在前面两列、也不能在后面两列,各列与18相除余数分别为1,3,5,7,9,11,13,15,17.
若和为1017,则中间数可能为113,而除以18的余数为3,
满足条件,其最小的数为95. ( 10分)
19.(2005河南课改实验区)在数学活动中,小明为了求的值(结果用n表示),设计如图7-1所示的几何图形。
(1)请你利用这个几何图形求
的值为__________。
(2)请你利用图7-2,再设计一个能求
的值的几何图形。
19.解:(1)。………………………………………………………………………4分
(2)如图1-1或如图1-2或如图1-3或如图1-4等,图形正确。……10分
归纳与猜想
18、(2005河北课改实验区)(本小题满分7分)
观察右面的图形(每个正方形的边长均为1)和相应等式,控究其中的规律:
①
②
③
④
……
⑴写出第五个等式,并在右边给出的五个正方形上画出与之对应的图示:
⑵猜想并写出与第n个图形相对应的等式。
18、解:⑴ ……………………………………………………2分
…………………………………………4分
⑵……………………………………………………7分
21. (2005安徽课改实验区)下图中, 图(1)是一个扇形AOB,将其作如下划分:
第一次划分: 如图(2)所示,以OA的一半OA1为半径画弧,再作∠AOB的平分线, 得到扇形的总数为6个, 分别为: 扇形AOB、扇形AOC、扇形COB、扇形A1OB1、扇形A1OC1、扇形C1OB1;
第二次划分: 如图(3)所示, 在扇形C1OB1中, 按上述划分方式继续划分, 可以得到扇形的总数为11个;
第三次划分: 如图(4)所示;
……
依次划分下去.
图(1) 图(2)第一次划分 图(3)第二次划分 图(4)第三次划分
(1) 根据题意, 完成下表:
划分次数 扇形总个数
1 6
2 11
3
4
… …
n
(2) 根据上表, 请你判断按上述划分方式, 能否得到扇形的总数为2005个 为什么
【解】
六、探索规律(本题满分12分)
划分次数 扇形总个数
1 6
2 11
3 16
4 21
21.(1)
9分
(2)不能够得到2005个扇形,因为满足的正整数不存在. 12分
④ ;
③1+2+5=32;
②1+3=22;
①1=12;
……
……
⑤ ;
我们知道:由于圆是中心对称图形,所以过圆心的任何一条直线都可以将圆分割成面积相等的两部分.
图12—1
m
m
m
m
图12—2
n
图12—3
图12—4
O
N
P
Q
M
C
C1
B1
A1
A
B
图15—1
O
N
P
Q
M
C
A
B
图15—2
你能行,加
油呀!
S1
S1>S2
S1
S1>S2
O
N
P
Q
M
C1
C2
B1
A1
A2
B2
图1
O
N
P
Q
M
C
A
B
C
A
B
图2
图中有规律哟!
图7-2
图7-1
