数学人教A版(2019)选择性必修第三册6.3.1二项式定理 课件(共19张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第三册6.3.1二项式定理 课件(共19张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 385.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-12 09:51:17 | ||
图片预览





文档简介
(共19张PPT)
我们在初中学习了(a+b)2=a2+2ab+b2,试写出(a+b)3,(a+b)4的展开式.
能用类比方法写出(a+b)n (n∈N*)的展开式吗?
(a+b)3=a3+3a2b+3ab2+b3,(a+b)4=a4+4a3b+6a2b2+4ab3+b4.
(a+b)n=
导课 ●明标
6.3.1二项式定理
学习目标:
1.正确理解二项式定理,能准确地写出二项式的展开式;(重点)
2. 会用二项展开式的通项公式求指定的项.(重点)
3.会用二项式定理解决与二项展开式有关的问题.(难点)
导课 ●明标
一.独学(自主学习);(5min)
内容:用心静心阅读课本P29-P31,进行圈点勾画,并思考问题:
1.观察
展开式,分析其运算过程,你能发现有什么规律?
2.你能写出(a+b)4的展开式吗?
3.写出(a+b)n的展开式?
二.组议(解决疑惑,交流方法).(3min)
重点讨论“(a+b)n的展开式”
(a+b)2=a2+2ab+b2 (a+b)3=a3+3a2b+3ab2+b3,.
自主 ●合作
展示 ● 质疑
1.观察
展开式,分析其运算过程,你能发现有什么规律?
(a+b)2=a2+2ab+b2 (a+b)3=a3+3a2b+3ab2+b3,.
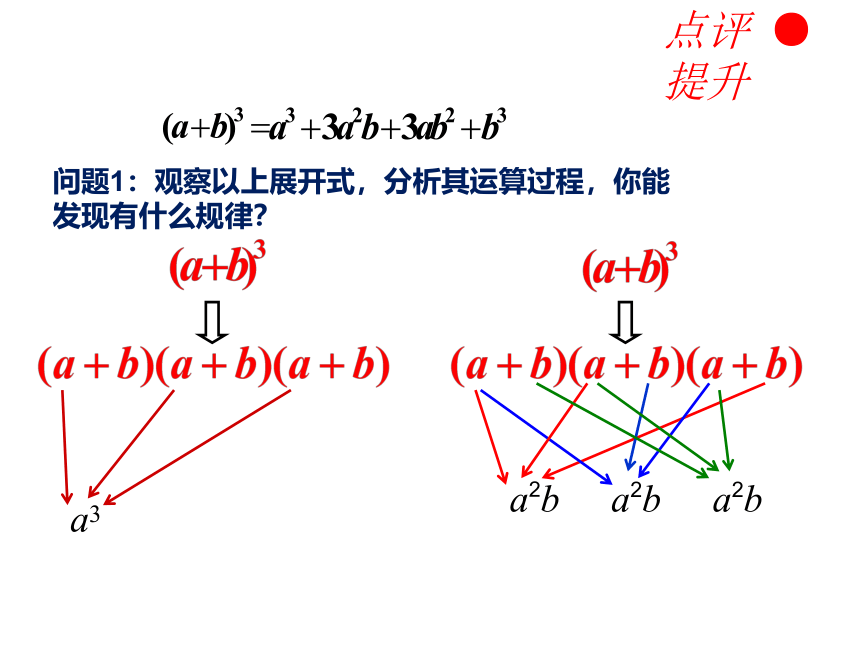
问题1:观察以上展开式,分析其运算过程,你能发现有什么规律?
a3
点评 ●提升
a2b
a2b
a2b
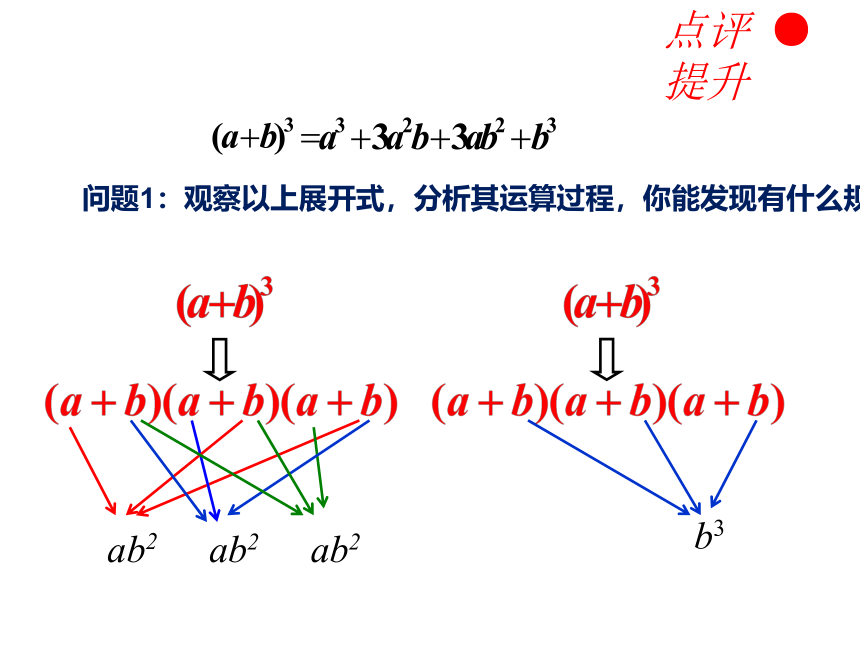
问题1:观察以上展开式,分析其运算过程,你能发现有什么规律?
ab2
ab2
ab2
点评 ●提升
b3
思考:
1.展开式有几项?如何得到?
2.每一项的形式为?
3.同类项的个数是多少?
点评 ●提升
展开式共有:
项的形式:
同类项的个数:
b3
点评 ●提升
点评 ●提升
展示 ● 质疑
点评 ●提升
问题2:你能写出(a+b)4的展开式吗?
展示 ● 质疑
3.写出(a+b)n的展开式?
点评 ●提升
二项式定理 公式(a+b)n= ,
称为二项式定理
二项式系数 _________________
通项 Tk+1=________
二项式定理 的特例
点评 ●提升
例1、
求 的展开式.
解:根据二项式定理,
训练 ●巩固
变式1:
求 的展开式.
解:根据二项式定理,
训练 ●巩固
例2:
解:
(1)
(2)
(3)
训练 ●巩固
根据题意,得
因此, 的系数是
求 的展开式中 的系数。
解:
的展开式的通项:
例3:
训练 ●巩固
1、二项式定理
2、二项展开式的通项
3、二项式系数:
总结●测评
1.求(x+2y)4的展开式.
=x4+8x3y+24x2y2+32xy3+16y4.
2.二项式(x+1)n(n∈N*)的展开式中x2的系数为15,则n等于( )
A.4 B.5
C.6 D.7
解得:n=6或-5(舍去).
C
总结●测评
我们在初中学习了(a+b)2=a2+2ab+b2,试写出(a+b)3,(a+b)4的展开式.
能用类比方法写出(a+b)n (n∈N*)的展开式吗?
(a+b)3=a3+3a2b+3ab2+b3,(a+b)4=a4+4a3b+6a2b2+4ab3+b4.
(a+b)n=
导课 ●明标
6.3.1二项式定理
学习目标:
1.正确理解二项式定理,能准确地写出二项式的展开式;(重点)
2. 会用二项展开式的通项公式求指定的项.(重点)
3.会用二项式定理解决与二项展开式有关的问题.(难点)
导课 ●明标
一.独学(自主学习);(5min)
内容:用心静心阅读课本P29-P31,进行圈点勾画,并思考问题:
1.观察
展开式,分析其运算过程,你能发现有什么规律?
2.你能写出(a+b)4的展开式吗?
3.写出(a+b)n的展开式?
二.组议(解决疑惑,交流方法).(3min)
重点讨论“(a+b)n的展开式”
(a+b)2=a2+2ab+b2 (a+b)3=a3+3a2b+3ab2+b3,.
自主 ●合作
展示 ● 质疑
1.观察
展开式,分析其运算过程,你能发现有什么规律?
(a+b)2=a2+2ab+b2 (a+b)3=a3+3a2b+3ab2+b3,.
问题1:观察以上展开式,分析其运算过程,你能发现有什么规律?
a3
点评 ●提升
a2b
a2b
a2b
问题1:观察以上展开式,分析其运算过程,你能发现有什么规律?
ab2
ab2
ab2
点评 ●提升
b3
思考:
1.展开式有几项?如何得到?
2.每一项的形式为?
3.同类项的个数是多少?
点评 ●提升
展开式共有:
项的形式:
同类项的个数:
b3
点评 ●提升
点评 ●提升
展示 ● 质疑
点评 ●提升
问题2:你能写出(a+b)4的展开式吗?
展示 ● 质疑
3.写出(a+b)n的展开式?
点评 ●提升
二项式定理 公式(a+b)n= ,
称为二项式定理
二项式系数 _________________
通项 Tk+1=________
二项式定理 的特例
点评 ●提升
例1、
求 的展开式.
解:根据二项式定理,
训练 ●巩固
变式1:
求 的展开式.
解:根据二项式定理,
训练 ●巩固
例2:
解:
(1)
(2)
(3)
训练 ●巩固
根据题意,得
因此, 的系数是
求 的展开式中 的系数。
解:
的展开式的通项:
例3:
训练 ●巩固
1、二项式定理
2、二项展开式的通项
3、二项式系数:
总结●测评
1.求(x+2y)4的展开式.
=x4+8x3y+24x2y2+32xy3+16y4.
2.二项式(x+1)n(n∈N*)的展开式中x2的系数为15,则n等于( )
A.4 B.5
C.6 D.7
解得:n=6或-5(舍去).
C
总结●测评
