19.1.2矩形第一课时[下学期]
文档属性
| 名称 | 19.1.2矩形第一课时[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-05-10 21:37:00 | ||
图片预览




文档简介
课件18张PPT。 龙南二中 袁建房复习提问1.什么叫做平行四边形?2.平行四边形有哪些性质?
特殊一般两组对边分别平行的四边形叫做平行四边形 .对边平行且相等.对角相等且邻角互补.
互相平分.
①边:
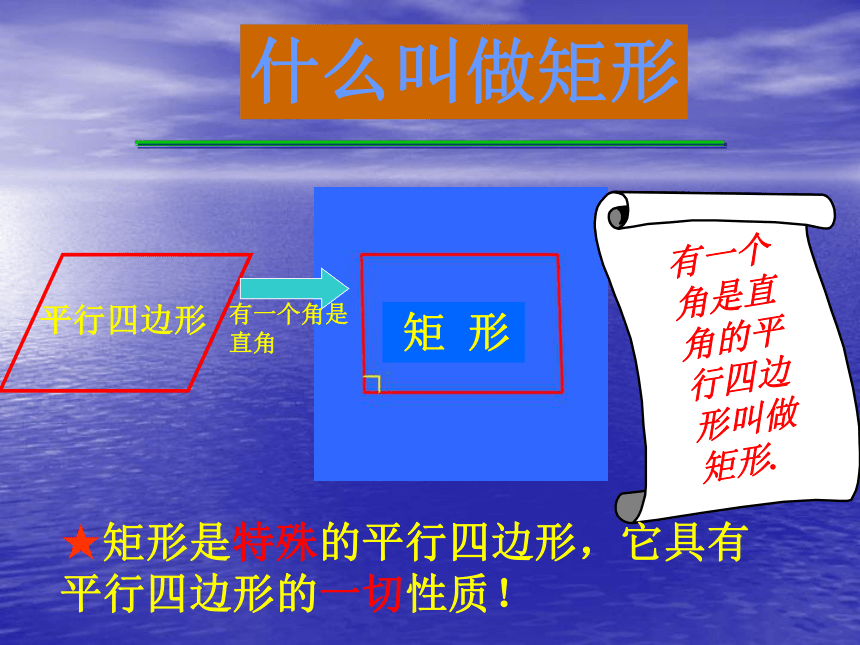
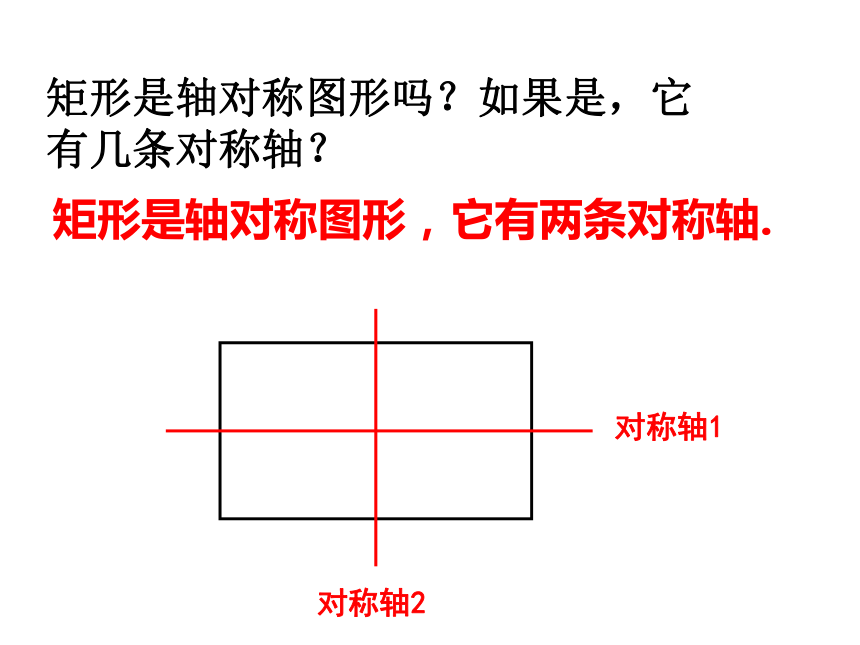
②角:③对角线:观察下面的演示平行四边形长方形有一个角是直角 矩 形有一个角是直角的平行四边形叫做矩形.★矩形是特殊的平行四边形,它具有平行四边形的一切性质!什么叫做矩形你见过生活中矩形的物体吗?矩形是轴对称图形吗?如果是,它有几条对称轴?矩形是轴对称图形,它有两条对称轴.
对称轴1对称轴2首先研究边的性质矩形的性质矩形的四个角都是直角.※ 矩形的性质1两条对角线有何关系?※ 矩形的性质2请证明这个命题!再来研究角的性质矩形的对边平行且相等.O做一做 在平行四边形活动框架上,用橡皮筋做出两条对角线,改变平行四边形的形状。(1) .随着∠D的变化,两条对角线的长度怎样变化?(2). 当∠D是直角时,平行四边形变成矩形,此时两条对角线的长度有什么关系?ABCD矩形的性质矩形的四个角都是直角.※ 矩形的性质1※ 矩形的性质2矩形的对边平行且相等.※ 矩形的性质3O矩形的对角线互相平分且相等.AB
C
D
O如图: OA =OC=______AC,
OB=OD=______BD,
OB是Rt△ABC的什么线?由此你可以得出什么结论?推论:
直角三角形斜边上的中线等于斜边的一半.
回顾:在直角三角形中,300的锐角所对的直角边等于斜边的一半结论△ABO和△DCO是全等的等腰三角形,△AOD与△BOC也是全等的等腰三角形。A
B
精选例题1.判断△AOB的形状
2.求对角线的长.
例1 已知:如图,矩形ABCD的两条对角线相交于点O , ∠AOB=60°,AB=4cm,
60oACDOB∴△OAB是等边三角形。(2)∵AB=4(cm), ∴OA=AB=4(cm)
∴矩形的对角线长AC=BD=2AO =8cm
60o解:(1)
∵四边形ABCD是矩形,∴AC与BD相等且互相平分。∴OA=0B又∠AOB=60o,
拓展延伸, 巩固深化如图:在梯形ABCD 中,AD∥BC, ∠B与
∠C互余,E、F分别为
AD、BC的中点,求
证:EF= (BC-AD)(1)你见过类似的题目吗?若见过,它们有哪些相同点,哪些不同点?你能把它转化为你熟悉的问题吗?(2)若没见过,你从题目中能发现哪些重要条件,它们与求证的结论有什么联系吗?(3)你能否把∠B 、∠C转移到一个三角形中去,把该问题转化为三角形的问题?(4)请试着过E点分别作AB、CD的平行线交BC于M、N点。完成后,你发现四边形ABME,四边形ENCD的形状吗?你还有其它的新发现吗?(5)在Rt△MEN中,你能根据我们这节课的内容发现EF与MN的数量关系吗?你找到了解题的方法吗?B1MFNCDEA分析点拨2
又∵AE=DE,
BF=CF∴BM=AE=DE=NC= AD
∴BC-AD=BC-MB-NC=MN BF-BM=CF-NC
即MF=NF ∴EF= MN
∴EF= (BC-AD)
B12MFNCDEA证明:过E点分别作AB、CD的平行线交BC于M、N
∵AE∥BM,AB∥EM
∴四边形ABME是平行四边形;同理,四边形ENCD是平行四形,
∴∠1=∠B,∠2=∠C,又∵∠B+∠C=90o, ∴∠1+∠2=90o, ∴△MEN为直角三角形;
1.矩形的定义:四边形两组对边
分别平行平行四边形
矩形有一个内角
是直角2.矩形的性质:对边平行且相等四个角都是直角对角线互相平分且相等边:角:对角线:推论:直角三角形斜边上的中线等于斜边的一半课本 :P104练习T1
T3
课后作业
特殊一般两组对边分别平行的四边形叫做平行四边形 .对边平行且相等.对角相等且邻角互补.
互相平分.
①边:
②角:③对角线:观察下面的演示平行四边形长方形有一个角是直角 矩 形有一个角是直角的平行四边形叫做矩形.★矩形是特殊的平行四边形,它具有平行四边形的一切性质!什么叫做矩形你见过生活中矩形的物体吗?矩形是轴对称图形吗?如果是,它有几条对称轴?矩形是轴对称图形,它有两条对称轴.
对称轴1对称轴2首先研究边的性质矩形的性质矩形的四个角都是直角.※ 矩形的性质1两条对角线有何关系?※ 矩形的性质2请证明这个命题!再来研究角的性质矩形的对边平行且相等.O做一做 在平行四边形活动框架上,用橡皮筋做出两条对角线,改变平行四边形的形状。(1) .随着∠D的变化,两条对角线的长度怎样变化?(2). 当∠D是直角时,平行四边形变成矩形,此时两条对角线的长度有什么关系?ABCD矩形的性质矩形的四个角都是直角.※ 矩形的性质1※ 矩形的性质2矩形的对边平行且相等.※ 矩形的性质3O矩形的对角线互相平分且相等.AB
C
D
O如图: OA =OC=______AC,
OB=OD=______BD,
OB是Rt△ABC的什么线?由此你可以得出什么结论?推论:
直角三角形斜边上的中线等于斜边的一半.
回顾:在直角三角形中,300的锐角所对的直角边等于斜边的一半结论△ABO和△DCO是全等的等腰三角形,△AOD与△BOC也是全等的等腰三角形。A
B
精选例题1.判断△AOB的形状
2.求对角线的长.
例1 已知:如图,矩形ABCD的两条对角线相交于点O , ∠AOB=60°,AB=4cm,
60oACDOB∴△OAB是等边三角形。(2)∵AB=4(cm), ∴OA=AB=4(cm)
∴矩形的对角线长AC=BD=2AO =8cm
60o解:(1)
∵四边形ABCD是矩形,∴AC与BD相等且互相平分。∴OA=0B又∠AOB=60o,
拓展延伸, 巩固深化如图:在梯形ABCD 中,AD∥BC, ∠B与
∠C互余,E、F分别为
AD、BC的中点,求
证:EF= (BC-AD)(1)你见过类似的题目吗?若见过,它们有哪些相同点,哪些不同点?你能把它转化为你熟悉的问题吗?(2)若没见过,你从题目中能发现哪些重要条件,它们与求证的结论有什么联系吗?(3)你能否把∠B 、∠C转移到一个三角形中去,把该问题转化为三角形的问题?(4)请试着过E点分别作AB、CD的平行线交BC于M、N点。完成后,你发现四边形ABME,四边形ENCD的形状吗?你还有其它的新发现吗?(5)在Rt△MEN中,你能根据我们这节课的内容发现EF与MN的数量关系吗?你找到了解题的方法吗?B1MFNCDEA分析点拨2
又∵AE=DE,
BF=CF∴BM=AE=DE=NC= AD
∴BC-AD=BC-MB-NC=MN BF-BM=CF-NC
即MF=NF ∴EF= MN
∴EF= (BC-AD)
B12MFNCDEA证明:过E点分别作AB、CD的平行线交BC于M、N
∵AE∥BM,AB∥EM
∴四边形ABME是平行四边形;同理,四边形ENCD是平行四形,
∴∠1=∠B,∠2=∠C,又∵∠B+∠C=90o, ∴∠1+∠2=90o, ∴△MEN为直角三角形;
1.矩形的定义:四边形两组对边
分别平行平行四边形
矩形有一个内角
是直角2.矩形的性质:对边平行且相等四个角都是直角对角线互相平分且相等边:角:对角线:推论:直角三角形斜边上的中线等于斜边的一半课本 :P104练习T1
T3
课后作业
