19.1.2矩形第一课时[下学期]
文档属性
| 名称 | 19.1.2矩形第一课时[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 853.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-10-19 00:00:00 | ||
图片预览


文档简介
课件16张PPT。矩 形平行四边形特性
矩形定义
矩形特征
直角三角形的特征
例1
例2例3练习1小结
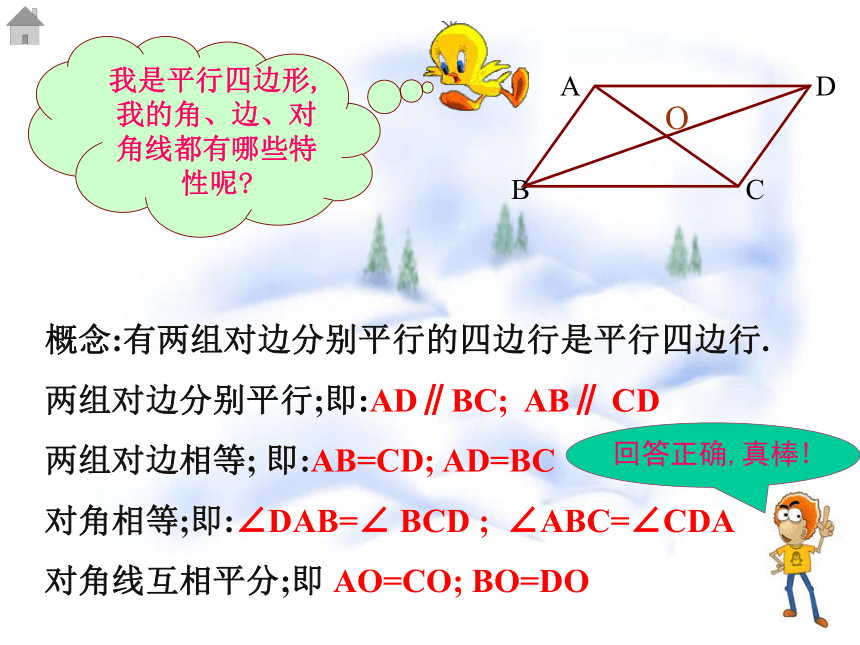
例题练习2寻乌毛泽东旧居矩形课 题我是平行四边形,我的角、边、对角线都有哪些特性呢?概念:有两组对边分别平行的四边行是平行四边行.
两组对边分别平行;即:AD∥BC; AB∥ CD
两组对边相等; 即:AB=CD; AD=BC
对角相等;即:∠DAB=∠ BCD ; ∠ABC=∠CDA
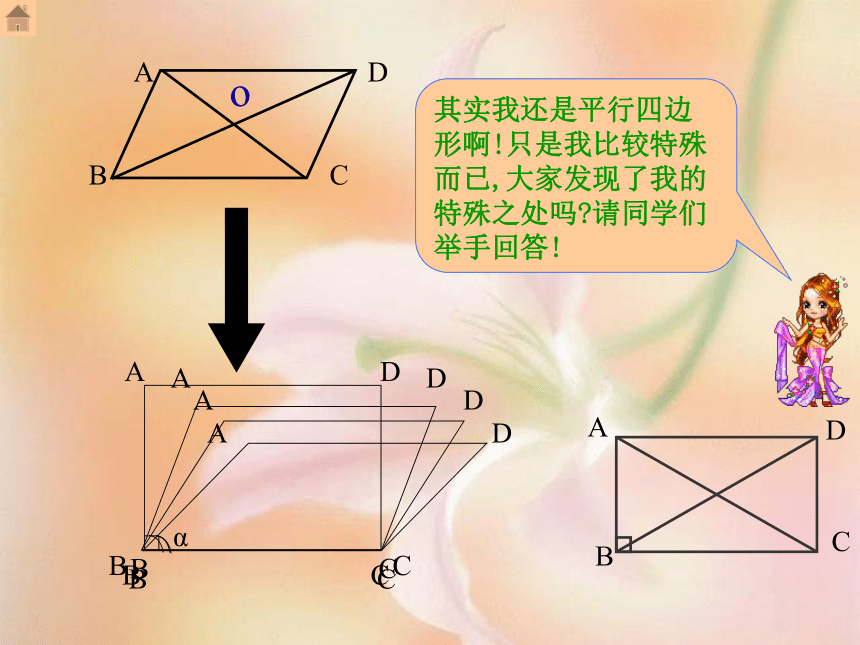
对角线互相平分;即 AO=CO; BO=DO平行四边形特性矩形:有一个角是直角的平行四边形。
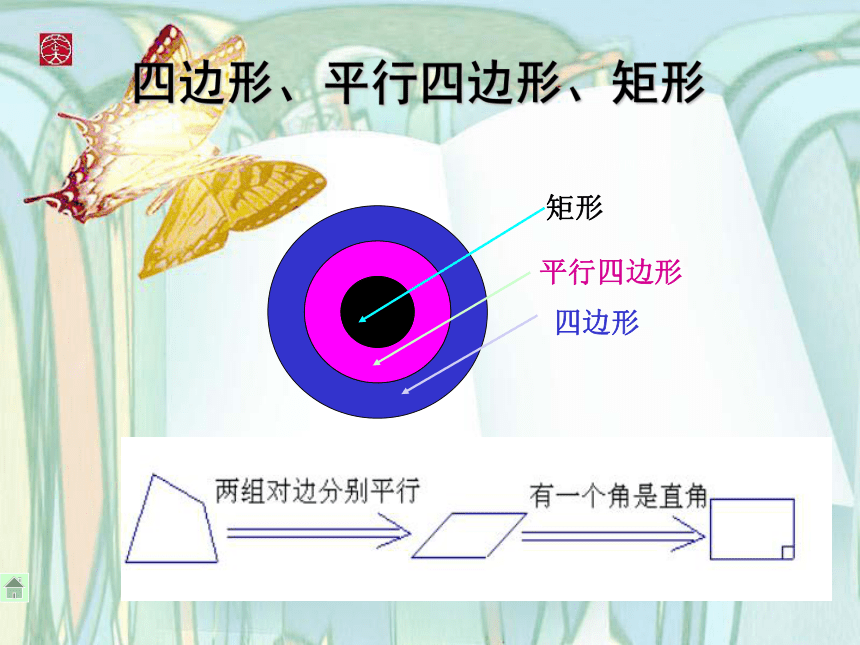
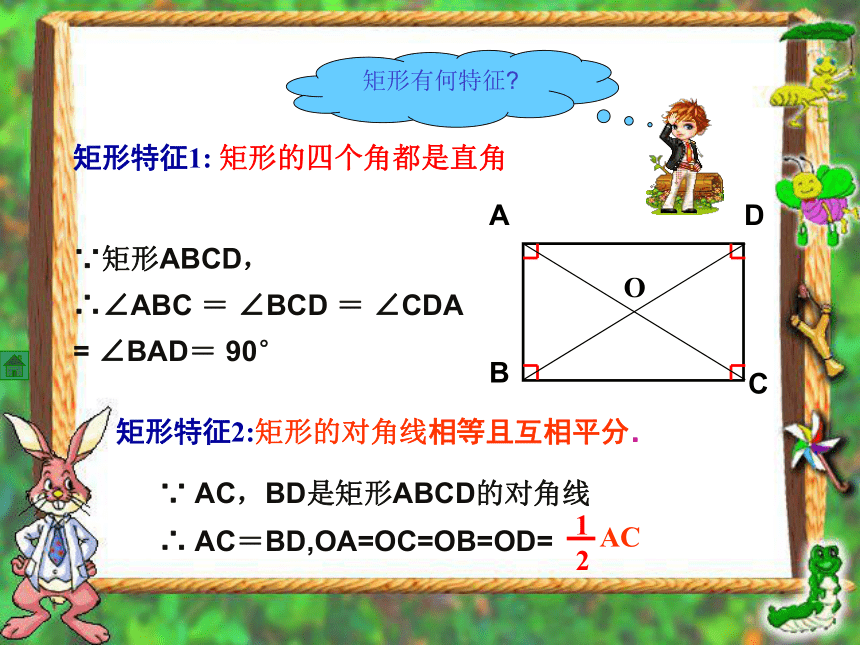
矩形是特殊 的平行四边形。特殊矩形定义四边形、平行四边形、矩形四边形平行四边形矩形矩形特征1: 矩形的四个角都是直角∵矩形ABCD,
∴∠ABC = ∠BCD = ∠CDA = ∠BAD= 90°矩形特征2:矩形的对角线相等且互相平分. ∵ AC,BD是矩形ABCD的对角线
∴ AC=BD,OA=OC=OB=OD=矩形特征直角三角形的特征因此可以得到:
直角三角形中斜
边的中线等于斜边的一半直角三角形特征例1 ∴ △AOB 是等边三角形
∴OA=OB=AB=1.5m ∴AC = 2OA=3m.(2)∵OB=OC ∠BOC=120° ∴ ∠ACB=30°假如已知窗户宽AB=1.5m,高AD=2m,你能求出木条的一半OA的长吗? ∴ OA= OB解:(1)∵四边形ABCD是矩形
∴AC 与 BD 相等且互相平分例2∵∠AOD=120°∴∠AOB=60°解? ∵AB + BC + CD + DA =7,
(BC + BO + CO)-(AB + AO + BO)= 0.5∴ AB + BC =3.5 BC-AB = 0.5
∴ AD = BC =2m,AB = CD =1.5m.又 ∵四边形ABCD是矩形
∴AB = CD,AD = BC
AO = CO=BO = DO练习1解: (1) ∵矩形ABCD ∴OD=OC
∴∠2= ∠ACD= 52°
例3∵ Rt△ADE 又 F是AE的中点
∴EF=DF ∴∠1=∠E=48°
∴∠ODF=180°-48°- 52°=80°
(2)∵ AE=2DF=2.5m
∴ DE2 = AE2 -AD2=2.25
∴ DE=1.5m
2、如图所示,这是我家客厅楼梯,
我准备在楼梯上铺设地毯,已知,
楼梯高AB=4米,长BC=6米,你能帮
我求出地毯的长吗?练习2四个角都是直角
(特性) 互相平分
相等(特性)
(2)角:(3)对角线:邻边:(1)边:对边:
平行
相等互相垂直一、矩形的定义二、矩形的特征小结脸蛋方方是矩形,例如黑板和窗门。对角线段皆相等,相互交叉且平分。内有直角三角形,斜边中线半斜边。若要牢记其定义,直角平行四边形。矩形之歌
矩形定义
矩形特征
直角三角形的特征
例1
例2例3练习1小结
例题练习2寻乌毛泽东旧居矩形课 题我是平行四边形,我的角、边、对角线都有哪些特性呢?概念:有两组对边分别平行的四边行是平行四边行.
两组对边分别平行;即:AD∥BC; AB∥ CD
两组对边相等; 即:AB=CD; AD=BC
对角相等;即:∠DAB=∠ BCD ; ∠ABC=∠CDA
对角线互相平分;即 AO=CO; BO=DO平行四边形特性矩形:有一个角是直角的平行四边形。
矩形是特殊 的平行四边形。特殊矩形定义四边形、平行四边形、矩形四边形平行四边形矩形矩形特征1: 矩形的四个角都是直角∵矩形ABCD,
∴∠ABC = ∠BCD = ∠CDA = ∠BAD= 90°矩形特征2:矩形的对角线相等且互相平分. ∵ AC,BD是矩形ABCD的对角线
∴ AC=BD,OA=OC=OB=OD=矩形特征直角三角形的特征因此可以得到:
直角三角形中斜
边的中线等于斜边的一半直角三角形特征例1 ∴ △AOB 是等边三角形
∴OA=OB=AB=1.5m ∴AC = 2OA=3m.(2)∵OB=OC ∠BOC=120° ∴ ∠ACB=30°假如已知窗户宽AB=1.5m,高AD=2m,你能求出木条的一半OA的长吗? ∴ OA= OB解:(1)∵四边形ABCD是矩形
∴AC 与 BD 相等且互相平分例2∵∠AOD=120°∴∠AOB=60°解? ∵AB + BC + CD + DA =7,
(BC + BO + CO)-(AB + AO + BO)= 0.5∴ AB + BC =3.5 BC-AB = 0.5
∴ AD = BC =2m,AB = CD =1.5m.又 ∵四边形ABCD是矩形
∴AB = CD,AD = BC
AO = CO=BO = DO练习1解: (1) ∵矩形ABCD ∴OD=OC
∴∠2= ∠ACD= 52°
例3∵ Rt△ADE 又 F是AE的中点
∴EF=DF ∴∠1=∠E=48°
∴∠ODF=180°-48°- 52°=80°
(2)∵ AE=2DF=2.5m
∴ DE2 = AE2 -AD2=2.25
∴ DE=1.5m
2、如图所示,这是我家客厅楼梯,
我准备在楼梯上铺设地毯,已知,
楼梯高AB=4米,长BC=6米,你能帮
我求出地毯的长吗?练习2四个角都是直角
(特性) 互相平分
相等(特性)
(2)角:(3)对角线:邻边:(1)边:对边:
平行
相等互相垂直一、矩形的定义二、矩形的特征小结脸蛋方方是矩形,例如黑板和窗门。对角线段皆相等,相互交叉且平分。内有直角三角形,斜边中线半斜边。若要牢记其定义,直角平行四边形。矩形之歌
