2014年人教新课标版七年级数学优质导学案第四章几何图形初步(22页)
文档属性
| 名称 | 2014年人教新课标版七年级数学优质导学案第四章几何图形初步(22页) |  | |
| 格式 | zip | ||
| 文件大小 | 514.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-09-18 19:35:11 | ||
图片预览

文档简介
第四章 几何图形初步
《4.1.1几何图形(1)》导学案NO:42
班级_______姓名_______小组_______小组评价_______教师评价_____
一、学习目标
1. 通过观察生活中的大量图片或实物,体验、感受、认识以生活中的事物为原型的几何图形,认识简单的几何体;
2.能由实物形状想象出几何图形,由几何图形想象出实物形状。
二、自主学习
1、请同学们阅读教材P116至P119第一行,完成下列填空:
(1)各种各样的物体,数学中只关注的是它们的 、 、
(2)有些几何图形的各部分不都在同一平面内,这样的几何图形叫做
(3)有些几何图形的各个部分都在同一平面内,这样的几何图形叫做
2、思考并回答下列各题:
(1)如图,下面是一些具体的物体与实物,试找出与立体图形类似的实物。
圣诞帽子 油桶 塔顶 西瓜
点拨:通过观察才能反映物体外观的主要特征,再抽象出具体的立体几何图形。
(2)下列几何体中(如图)属于棱锥的是( )
(1) (2) (3) (4) (5) (6)
A、①⑤ B、① C、①⑤⑥ D、⑤⑥
3、自学检测
(1)完成教材P119的练习;
(2)下面几种图形:①三角形;②长方形; ( http: / / www.21cnjy.com )③正方形;④圆;⑤圆锥;⑥圆柱。其中属于平面图形的是 ,属于立体图形的是
三、合作探究
1. 奥运会的标志是五环,每一个环的形状与 ( http: / / www.21cnjy.com )__类似;①电视机、②铅笔、③西瓜、④烟囱帽 ___与足球的形状类似;古埃及金字塔类似于几何体 。
2.月球、西瓜、易拉罐、篮球、热水瓶胆、书本等物体中,形状类似圆柱的有 个。
3.下列图形中,不是立体图形的是( )
A、球 B、圆 C、圆锥 D、圆柱
4.下列立体图形中,属于柱体的是( )
( http: / / www.21cnjy.com )
5.长方体属于( )A、棱锥 B、棱柱 C、圆柱 D、以上都不对
6.下列几何体中,不完全由平面围成的是( )
四、达标检测
1.完成教材P123的习题4.1第1、2题;
2.把下面几何体的标号写在相对应的括号里.
长方体有:{ } 棱柱体有:{ }
圆柱体有:{ } 球 体有:{ }
圆锥体有:{ }
五、拓展提高
由棱长是1cm 的若干个小正方体组成如图所示的几何体,那么这个几何体的表面积是( )
A、36cm B、33cm C、30cm D、27cm
分析:从不同的方向观察该几何体,想象图形的每一层
是由几个小正方体组成的,再由正方体的表面积公式计算。
《4.1.1几何图形(2)》导学案NO:43
班级_______姓名_______小组_______小组评价_______教师评价_____
一、学习目标
1. 经历从不同方向观察物体的活动过程,初步体会从不同方向观察同一物体可能看到不一样的结果;能作出一些简单物体的三视图;
2.了解多面体平面展开图,重点是正方体、圆锥、圆柱的平面展开图;能根据展开图初步判断和制作立体模型;
二、自主学习
1、请同学们阅读教材P119至P120,对 ( http: / / www.21cnjy.com )于一些立体图形的问题,我们通常把它们转化为平面图形来研究和处理。从不同方向看立体图形,往往会得到不同形状的平面图形。我们通常从三个方面看,即 、 、 。有些立体图形是由一些平面图形围成的,将它们的表面适当剪开,可以展开成 。这样的 称为相应立体图形的展开图。
2、请同学们对这个部分的两个探究进行动手操作,通过实际观察体会对立体图形的三视图及展开图。
3、自学检测
(1)完成教材P120的练习1、2题;
(2)如图所示,该物体从上往下看是( )
(3)下面六个正方形连在一起的图形,经折叠后能围成正方体的图形是 。
三、合作探究
1、从正面看、从左面看、从 ( http: / / www.21cnjy.com )上面看都一样的几何体是 、 ;从上面看一个几何体所形成的图形是圆,这个几何体可能是 。
2、如图是用4个长方体搭成的图形,从左面看,它应是下列图形中的( )
3、 如图,把左边的图形折叠起来,它会变为( )
( http: / / www.21cnjy.com )
4、如图,太阳在房子的后方,那么房子在地面上的影子是( )
5、观察右上图,这是由一些相同小正方体构成的立体图形的三种视图,构成这个立体图形的小正方体的个数是______
6.想一想,哪种几何体的表面展开成如下的平面图形,画出表示这些几何体的立体图形.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
四、达标检测
1、完成课本P124第3、4、5、6题;
2、一个几何体,是由许多规格相同的小正 ( http: / / www.21cnjy.com )方体堆积而成的,某主视图、左视图如图所示,要摆成这样的图形,至少需用________块正方体,最多需用_________正方体.
五、拓展提高
如图所示,一只昆虫要沿正方体表面从正方体的一个顶点A爬到相距它最远的另一个顶点,画出它爬行的最短路线?
《4.1.4点、线、面、体》导学案NO:44
班级_______姓名_______小组_______小组评价_______教师评价_____
一、学习目标
1. 探究点、线、面、体的几何特征,感受它们之间的关系;
2.感知正方体、圆锥、圆柱的展开图的特点。
二、自主学习
1、请同学们阅读教材P121至123第四行,完成下列填空:
(1)生活中有各种各样的立体图形,常见的几何体有 、 、 、
、 、 、球等。
(2)包围着体的是 。面有 和 两种。
(3)任何一个几何体都由 、 、 构成,平面是无限延伸的,面有平面和曲面,面面相交得 ,线线相交得 。点动成 ,线动成 ,面动成 。点、线、面、体都是几何图形。
2、自学检测:
(1)完成教材P122练习;
(2)笔尖在纸上划过就能写出汉字, ( http: / / www.21cnjy.com )这说明了______;汽车的雨刮器摆动就能刮去挡风玻璃上的雨滴,这说明了______;长方形纸片绕它的一边旋转形成了一个圆柱体,这说明了______.
(3)在下列几何体中,不能展开成平面图形的是( )
A、棱柱 B、圆柱 C、圆锥 D、球
三、合作探究
1. 按组成面的侧面“平”与“曲”划分,与圆柱为同一类的几何体是( )
A、圆锥 B、长方体 C、正方体 D、棱柱
2.圆锥的侧面展开图不可能是( )
A、小半个圆 B、半个圆 C、大半圆 D、圆
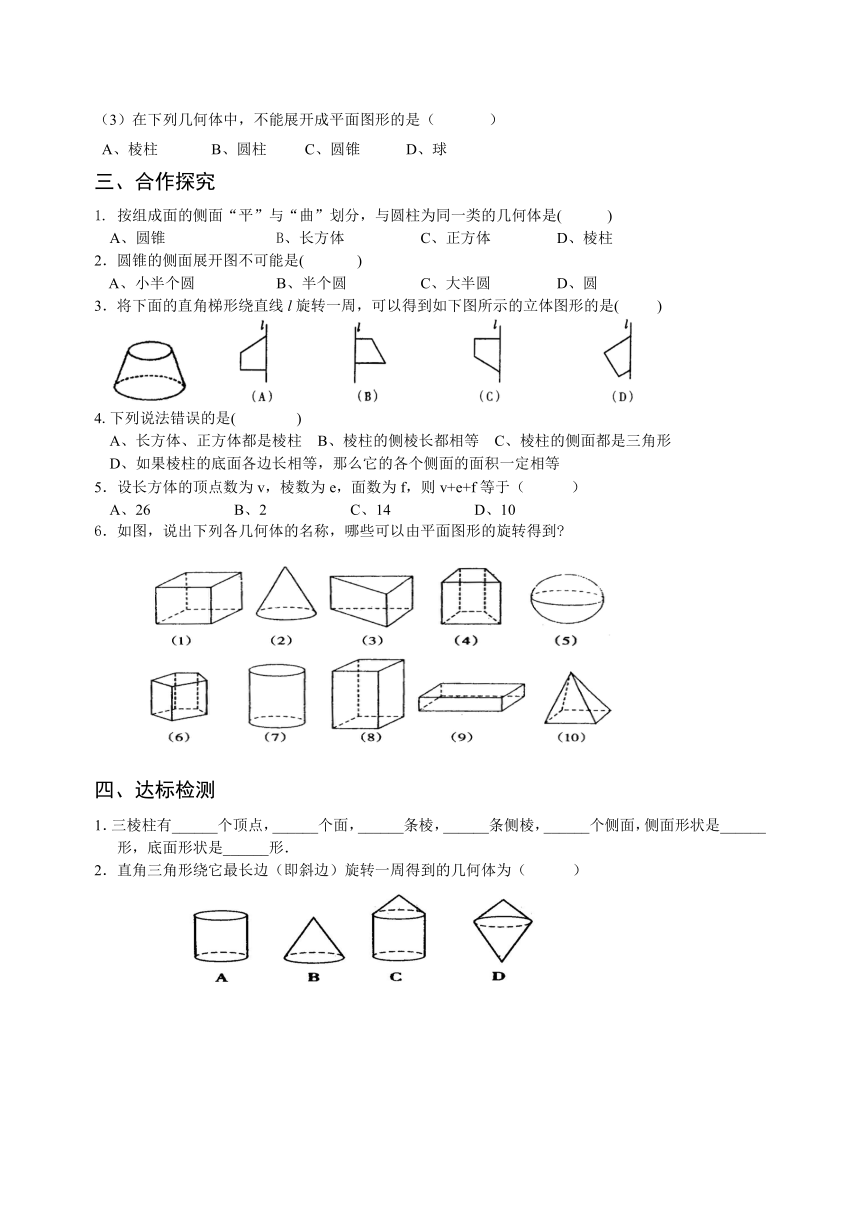
3.将下面的直角梯形绕直线l旋转一周,可以得到如下图所示的立体图形的是( )
4.下列说法错误的是( )
A、长方体、正方体都是棱柱 B、棱柱的侧棱长都相等 C、棱柱的侧面都是三角形
D、如果棱柱的底面各边长相等,那么它的各个侧面的面积一定相等
5.设长方体的顶点数为v,棱数为e,面数为f,则v+e+f等于( )
A、26 B、2 C、14 D、10
6.如图,说出下列各几何体的名称,哪些可以由平面图形的旋转得到
四、达标检测
1.三棱柱有______个顶点,______个面,______条棱,______条侧棱,______个侧面,侧面形状是______形,底面形状是______形.
2.直角三角形绕它最长边(即斜边)旋转一周得到的几何体为( )
3.如图,把第一行的图形绕虚线旋转一周便能形成第二行的某个几何体,请用线连起来.
五、拓展提高
有一个长为4cm、宽为3cm的长方形,分别绕它的长、宽所在直线旋转一周,得到不同的圆柱体,它们的体积分别是多大?
《4.2.1直线、射线、线段》导学案NO:45
班级_______姓名_______小组_______小组评价_______教师评价_____
一、学习目标
1.探究直线、射线、线段的联系和区别,掌握它们的表示方法;
2.理解两点确定一条直线的事实,并体会它在解决实际问题中的作用;
二、自主学习
1、请同学们自学教材P128至P129倒数第四行,并完成下列填空:
(1)直线、射线、线段的比较
直 线 射 线 线 段
相似处
端 点
延伸方向
图 形
表示法
注意:①线段、直线的表示与字母 无关;②射线的表示有方向性,
在前,射线上任意一点在后。
(2)直线:直线的公理 ( http: / / www.21cnjy.com ) (大声朗读三遍);点与直线的位置关系有两种:① ;②
2、自学检测:
(1)完成教材P129的练习题;
(2)要把木条固定在墙上至少要钉______个钉子,这是因为___________________;
(3)如图,点O在线段AB______;点B在射线AB______;
点A是线段AB的一个______.
三、合作探究
1.经过一点的直线有______条;经过两点的直线有______条,并且______一条。
2.把线段向一个方向延长,得到的是________;把线段向两个方向延长,得到的是______.
3.线段有______个端点,射线有______个端点,直线有______个端点.
4.如图,图中有______条射线,______条线段,
这些线段是_______ ___
5.如图,AC,BD交于点O,图中共有______条线段,
它们分别是____ __
6.如图,图中有____ ( http: / / www.21cnjy.com )__条线段,它们是______图中以A点为端点的射线有______条,它们是______图中有______条直线,它们是______
7.根据“反向延长线段CD”这句话,下图表示正确的是( )
8.如图所示,有直线、射线和线段,根据图中的特征判断其中能相交的是( )
四、达标检测
1.下列说法中正确的有( )
①钢笔可看作线段,②探照灯光线可看作射线,③笔直的高速公路可看作一条直线,
④电线杆可看作线段
(A)1个 (B)2个 (C)3个 (D)4个
2.下列说法中正确的语句共有( )
①直线AB与直线BA是同一条直线, ② ( http: / / www.21cnjy.com )线段AB与线段BA表示同一条线段,③射线AB与射线BA表示同一条射线,④延长射线AB至C,使AC=BC,⑤延长线段AB至C,使BC=AB,⑥直线总比线段长.
(A)2个 (B)3个 (C)4个 (D)5个
3.作图:
(1)点P在直线AB上,点M在直线AB外.
(2)直线AB、CD交于点O,点M在直线AB上,但不在CD上.
(3)经过点O的三条直线a,b,c.
五、拓展提高
看图写话
(1) ( http: / / www.21cnjy.com ) (2)
《4.1.1线段的大小比较》导学案NO:46
班级_______姓名_______小组_______小组评价_______教师评价_____
一、学习目标
1.结合图形认识线段间的数量关系,学会比较线段的大小;
2.理解两点之间线段最短的性质并能初步应用。知道两点之间的距离和线段中点的含义。
二、自主学习
1、请同学们自学教材P129至132第五行,并完成下列填空:
(1)仔细观察P129至P130中的图 ( http: / / www.21cnjy.com )形,比较两条线段的长短的方法有两种:(1)把它们放在同一条直线上比较,这种方法称为 法;2)用刻度尺去度量它们的长度进行比较,这种方法称为
(2)如图所示:点M把线段AB分成 ( http: / / www.21cnjy.com )相等的两条线段AM与BM,点M叫做线段AB的中点。这时AM=BM= AB,AB= AM= BM (默记)
(3)线段的性质:两点之间, 最短。(读三遍记忆)
(4)连接两点的线段的 ,叫做这两点之间距离。(读三遍)
2、典例解析
例、已知线段AB=14,在直线AB上有一点C,且BC=4,D是线段AC的中点,求线段AD的长。(请注意解题格式与步骤)
解:(1)当点C在线段AB上时(如图)
AC=AB-BC=14-4=10
D是AC的中点
AD=AC==5
(2)当点C在线段AB延长线上时(如图)
3、自学检测
(1)、完成教材P131练习;
(2)、已知A、B、C为直线上的三点,线段AB=9cm,BC=1cm,那A、C两点间的距离是( )
三、合作探究
1.若A、B、C、D为直线上顺次四点(如图所示),则AB+BD=AC+______;AC+BD=AD+____ __
2.若点C在线段AB的延长线上,则AC与AB的大小关系是______,并且AB+BC=______,AC-AB=______.
3.如图,A是直线BC外一点,请用不等号分别连接下列各式。
AB+AC______BC;AB+BC______AC;AC+BC______AB.
想一想:AB-AC________BC
4.已知线段OA=5cm,OB=3cm,则下列说法正确的是( )
A.AB=2cm B.AB=8cm
C.AB=4cm D.不能确定AB的长度
5.已知线段AB=10cm,AP+BP=20cm.下列说法正确的是( )
A.点P不能在直线AB上 B.点P只能在直线AB上
C.点P只能在线段AB的延长线上 D.点P不能在线段AB上
6.如图,延长线段AB到C,使D为AC的中点,DC=2,求AB的长.
四、达标检测
1.根据图形填空
(1)如图,若AB=BC=CD=DE,那么
①AE=______AB, ②AC=______AE,
③AD=______AE, ④CE=______AD.
(2)如图,已知D、E分别是线段AB、 BC的中点,
①若AB=3cm,BC=5cm,则DE=______cm;
②若AC=8cm,EC=3cm,则AD=______cm.
2.已知数轴上的三点A,B,C所对应的数 ( http: / / www.21cnjy.com )a,b,c满足a<b<c,abc<0和a+b+c=0,那么线段AB与BC的大小关系是( )
A.AB>BC B.AB=BC C.AB<BC D.不确定
3.已知C为线段AB的中点,AB=10cm,D是AB上一点,若CD=2cm,求BD的长.
五、拓展提高
12.已知C,D两点将线段AB分为三部分,且AC∶CD∶DB=2∶3∶4,若AB的中点为M,BD的中点为N,且MN=5cm,求AB的长.
《4.3.1角(1)》导学案NO:47
班级_______姓名_______小组_______小组评价_______教师评价_____
一、学习目标
1.掌握角的两种定义形式和四种表示方法;
2.通过在图片、实例中找角,体会角在实际生活中的应用。
二、自主学习
1、请同学们自学教材P 136,并完成下列填空:
(1)①____________的图 ( http: / / www.21cnjy.com )形叫做角,____________________叫做角的顶点,_____________________叫做角的边.(读三遍)
②角也可以看作是由一条_________绕着它的__________而形成的图形,这条射线的起始位置叫做角的______,其终止位置叫做角的________.(读三遍)
(2)角的表示法
①用一个数字,如; ②用一个大写字母,
如;(在角的顶点有几个角时不能用一个大写字母表示)
③用三个大写字母,如∠ABC;(顶点的字母写在中间)
④用一个希腊字母,如。
(3)一条射线绕其端点O按逆时 ( http: / / www.21cnjy.com )针方向旋转得到∠AOB,当角的终边OB旋转到与角的始边OA成一条直线时,称∠AOB为______;若角的终边继续旋转,当角的终边OB与角的始边OA重合时,称∠AOB为______.
2、自学检测:完成教材P138练习第1题及P143习题4.3第1、2题。
三、合作探究
1.下列说法正确的是( )
A、一个周角就是一条射线 B、平角是一条直线
C、角的两边越长,角就越大 D、∠AOB也可以表示为∠B
2.下列4个图形中,能用∠1、∠AOB、∠O三种方法表示同一角的图形是( )
3.如图所示,点O在直线AB上,图中小于180°的角
共有( ).
A、7个 B、8个 C、9个 D、10个
4.如图,(1)中有______个角,(2)中有______个角;(3)中
有______个角.以此类推,若一个角内有n条射线,则可有______个角.
5.如图,图中能用一个大写字母表示的角有 个。分别把它们表示出来________________________
四、达标检测
1.下列关于角的说法正确的个数是( )
①角是由两条射线组成的图形;②角的边越长,角越大; ③在角一边延长线取一点; ④角可以看作由一条射线绕着它的端点旋转而形成的图形.
A、1个 B、2个 C、3个 D、4个
2.图中共有______个小于平角的角,它们分别是_______________其
中以D为顶点的小于平角的角有______个.
3.图中以OC为边的角有______个,它们分别是______
五、拓展提高
2.用三个字母表示图中所注的∠1、∠2、∠3、∠4:
(1) (2)
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(1)∠1是______;∠2是______;∠3是______;
(2)∠1是______;∠2是______;∠3是______; ∠4是______.
《4.3.1角(2)》导学案NO:48
班级_______姓名_______小组_______小组评价_______教师评价_____
一、学习目标
1.掌握角度的换算关系;
2.能进行角的简单的加、减、乘、除运算。
二、自主学习
1、请同学们自学教材P137,并完成下列填空:
以度、分、秒为单位的角度制规定,把一个 ( http: / / www.21cnjy.com )周角______,每一份叫做1度,记作______;把1度的角______,每一份叫做1分,记作______;把1分的角______,每一份叫做1秒,记作______.这样1周角是______°,1平角是______°,1°=______',1′=______″.
2、典例解析
例1.下列算式正确的是( )
① ② ③
④ A ①和② B①和③ C②和③ D②和④
思路分析:角度的换算只要注意度化分乘以60,分化秒乘以60;分化度除以60,秒化分除以60 ;
例2.计算(1)49°38′+66°22′ (2)180°-79°19′
(3)22°16′×5 (4)182°36′÷4.
3、自学检测
完成教材P138第2、3题及P143第3题。
三、合作探究
1.将一个周角分成360份,其中每一份是_____°的角,直角等于____°,平角等于______°
2.计算
(1)0.4°=______' (2)0.6′=______″
(3)24′=______° (4)12″=______′
(5)57.32°=______°______′______″
(6)17°14′24″=______°
(7)17°40′÷3=______°______′______″
(8)25°36′18″×6=______°______′______″
3.若,则、、( )
A 都是锐角 B 都是钝角 C 两个锐角,一个钝角 D 至少有两个锐角
4.两个锐角相加一定是( )
A 锐角 B 钝角 C 直角 D以上均有可能
5.计算:(2)180°—79°19′ (3)22°16′×5
6.时钟的时针1小时旋转多少度 时钟的分针1分钟旋转多少度 2点整时,时钟的时针与分针之间的夹角是多少度 3点呢?
四、达标检测
1. 直角= 平角= 周角。
2.若,则( )
A B C D 以上都不对
3. 计算
(1)49°38′+66°22′ (2)182°36′÷4 (3)32°16′25″×4-78°25′
五、拓展提高
时钟在8:30时,时针与分针的夹角为多少度 从6时到7时,钟表面上的时针与分针何时成的角?
《4.3.2角的比较与运算》导学案NO:49
班级_______姓名_______小组_______小组评价_______教师评价_____
一、学习目标
1.了解角度的比较方法,掌握角度的和差倍分关系。
2.掌握角平分线的定义和性质,能运用角平分线解决简单的角度问题。
二、自主学习
请同学们自学教材P138至P140,完成下列填空:
1、角的比较:①与线段长短的比较相类似,比较两个角的大小有2种方法:
方法一为:_________________________;方法二为:__________________________
②思考:在上右图中共有几个角,怎么数的?
在图中表示出来。
在右图中,
∠AOB=_________+____________
∠BOC=________________-__________
2、角的平分线
(1)、如图,如果∠AOC=∠BOC,那么射线OC是∠AOB的角平分线。
角平分线的定义:_______________________________________________(读三遍)
符号语言:∵OC平分∠AOB
∴∠AOC=∠BOC
(∠AOB=2∠ 或∠AOB =2∠ ;
或∠AOC=∠ ,∠BOC =∠_____ )
(2)、请画出下面两个角的角平分线,
3、例题示范
例、O是直线AB上一点,
∠AOC=53°,OD平分∠BOC,
求∠BOD的度数?(请注意解题格式与步骤)
4、自学检测
完成教材P140至P141练习。
三、合作探究
1、如下图,用“=”或“>”或“<”填空
(1)∠AOC_______∠AOB+∠BOC
(2)∠AOC_______∠AOB
(3)∠BOD-∠BOC______∠DOC
(4)∠AOD______∠AOC+∠BOD
2、如图,OB是平角∠AOC的角平分线,OD平分∠BOC,求∠AOD的度数。
3、如图,OB是∠AOC的平分线,OD是∠COE的平分线。
⑴如果∠AOB=40°,∠DOE=30°,那么∠BOD是多少度?
⑵如果∠AOE=140°,∠COD=30°,那么∠AOB是多少度?
四、达标检测
1.在小于平角的∠AOB的内部取一点C,并作射线OC,则一定存在( ).
(A)∠AOC>∠BOC (B)∠AOC=∠BOC
(C)∠AOB>∠AOC (D)∠BOC>∠AOC
2.按图填空:
(1)∠ABC是∠ABD与∠DBC的_____;(2)∠BDC是∠ADC与∠ADB的______.
(3)如果BD平分∠ABC,则∠ABD=________= ____ ∠ABC。
五、拓展提高
如图,∠AOB=90°,∠BOC=30°,OM平分∠AOB,ON平分∠BOC,
⑴求∠MON的度数,
⑵若∠AOB=∠α,若∠BOC=∠β(∠β为锐角)其他条件不变,求∠MON的度数。(用含α、β的式子表示)
⑶探究:从⑴⑵中你发现有什么规律?
《4.3.3余角和补角》导学案NO:50
班级_______姓名_______小组_______小组评价_______教师评价_____
一、学习目标
1.认识一个角的余角和补角,探究余角和补角的性质;
2.了解方位角,能确定具体物体的方位,学会简单的逻辑推理。并能对问题的结论
二、自主学习
1、请同学们自学P141至P143第四行,并完成下列填空与探究:
(1)①如果两个角的和是 ,那么这两个角叫做互为余角,其中一个角是另一个角的余角。即∠1是∠2的余角或∠2是∠1的余角。
②如果两个角的和是 ,那么这两个角叫做互为补角,其中一个角是另一个角的补角。即∠3是∠4的补角或∠4是∠3的补角。
(2)探究余角的性质:如右下图∠1 与∠2互余,
∠3 与∠4互余 ,如果∠1=∠3,那么∠2与∠4相等吗,为什么?
(3)探究补角的性质
请同学们自已作图探究,∠1 与∠2互补,∠3 与∠4互补 ,如果∠1=∠3,那么∠2与∠4相等吗,为什么?(对余角和补角的性质读三遍)
2、例题解析
例1、若一个角的补角等于它的余角4倍,求这个角的度数。
解: 设这个角是x °,则它的补角是( ),余角是( ) 。
根据题意得:
( )= 4 ( )
解之得: x =( )
答:这个角的度数是 。
例2、如图,∠AOB=90°,∠COD=∠ ( http: / / www.21cnjy.com )EOD=90°,C,O,E在一条直线上,且∠2=∠4,请说出∠1与∠3之间的关系?并试着说明理由?
3、自学检测:完成P141练习及P144第8、9题。
三、合作探究
1. 一个角的补角是它的3倍,这个角是
2. 如图∠AOB = 90 °,∠COD = 90 °,则∠1 ∠2.
3.A看B的方向是北偏东21°,那么B看A的方向( )
A、南偏东69° B、南偏西69° C、南偏东21° D、南偏西21°
4.如图,下列说法中错误的是( )
A、OC的方向是北偏东60° B、 OC的方向是南偏东60°
C、OB的方向是西南方向 D、 OA的方向是北偏西22°
5.如图.货轮O在航行过程中 ( http: / / www.21cnjy.com ),发现灯塔A在它南偏东60°的方向上,同时在它北偏东40°,南偏西10°,西北(即北偏西45°)方向上又分别发现了客轮B,货轮C和海岛D.仿照表示灯塔方位的方法画出表示客轮B,货轮C和海岛D方向的射线.
四、达标检测
1.70°的余角是 ,补角是 。
∠(∠ 90°)的它的余角是 ,它的补角是 。
2.在点O 北偏西60°的某处有一点A,在点O南偏西20°的某处有一点B,则
∠AOB的度数是( )A、100° B、70° C、180° D、140°
3.(1)一个角的余角为54°求这个角的补角的度数.
(2)两个角的比是7∶3,它们的差是72°,求这两个角的度数.
五、拓展提高
已知∠ 的余角是∠ 的补角的并且求∠ +∠ 的值.
《图形认识初步》复习学案NO:51
班级_______姓名_______小组_______小组评价_______教师评价_____
一、知识点回顾
(一)多姿多彩的图形
立体图形:棱柱、棱锥、圆柱、圆锥、球等。
1、几何图形
平面图形:三角形、四边形、圆等。
主(正)视图---------从正面看
2、几何体的三视图 侧(左、右)视图-----从左(右)边看
俯视图---------------从上面看
3、立体图形的平面展开图
(1)同一个立体图形按不同的方式展开,得到的平现图形不一样的。
(2)了解直棱柱、圆柱、圆锥的平面展开图,能根据展开图判断和制作立体模型。
4、点、线、面、体
(1)几何图形的组成:点、线、面、体。
(2)点动成线,线动成面,面动成体。
(二)直线、射线、线段
1、基本概念(请同学们从它们的图形、端点个数、表示法、作法叙述、延长叙述这五个方面列表比较)
2、直线的性质:两点确定一条直线。
3、画一条线段等于已知线段:(1)度量法 (2)用尺规作图法
4、线段的大小比较方法 :(1)度量法 (2)叠合法
5、线段的中点(二等分点):定义:把一条线段平均分成两条相等线段的点。
图形:
A M B
符号:若点M是线段AB的中点,则AM=BM=AB,AB=2AM=2BM。
6、线段的性质:两点之间,线段最短。
7、两点的距离:连接两点的线段长度叫做两点的距离。
8、点与直线的位置关系:(1)点在直线上 (2)点在直线外。
(三)角
1、角:由公共端点的两条射线所组成的图形叫做角。
2、角的表示法(四种):
3、角的度量单位及换算
4、角的分类:锐角、直角、钝角、平角、周角
5、角的比较方法:(1)度量法 (2)叠合法
6、角的和、差、倍、分及其近似值
7、画一个角等于已知角
8、角的平线线
定义:从一个角的顶点出发,把这个角分成相等的两个角的射线叫做角的平分线。
图形: 符号:
9、互余、互补的概念及性质
10方向角:正方向、北(南)偏东(西)方向、东(西)偏北(南)方向
二、巩固练习
1、计算:30.26°=____ °____′____″; 18°15′36″ =____ __ °;
36°56′+18°14′=____ ; 108°- 56°23′ =________;
27°17′×5 =____ ; 15°20′÷6 =____ (精确到分)
2、下列说法中正确的是( )
A、延长射线OP B、延长直线CD
C、延长线段CD D、反向延长直线CD
3、下面是我们制作的正方体的展开图,每个平面内都标注了字母,请根据要求回答问题:
(1)和面A所对的会是哪一面?
(2)和B面所对的会是哪一面?
(3)面E会和哪些面相交?
4、已知平面内有四个点A、B、C、D,过其中任意两点画直线,最少可画多少条直线,最多可画多少条直线?画出图来.
5、已知点B是线段AD的中点,点C是线段BD的中点,CD=2.5厘米,请你求出线段AB、AC、AD、BD的长各为多少?
6、已知线段AB=4厘米,延长AB到C,使B C=2AB,取AC的中点P,求PB的长.
7、如图,∠AOB是直角,OD平分∠BOC,OE平分∠AOC,求∠EOD的度数。(10分)
《图形认识初步》训练学案NO:52
班级_______姓名_______小组_______小组评价_______教师评价_____
一、选择题
1.如图,下列图形中,不是正方体展开图的是( )
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
A B C D
2.正方体的截面不可能构成的平面图形是( )
A.矩形 B.六边形 C.三角形 D.七边形
3.如果两个角互为补角,而其中一个角比另一个角的4倍少30°,那么这两个角是( )
A.42°,138°或40°,130°; B.42°,138°;
C.30°,150°; D.以上答案都不对
4. 已知点A、B、C都是直线l上的点,且AB=5cm,BC=3cm,那么点A与点C之间的距离是( )
A.8cm B.2cm或6cm C.8cm或2cm D.4cm
5. 下列图形中,能够相交的是 ( )
6.甲从O点出发,沿北偏西30°走了50米到达A点,乙也从O点出发,沿南偏东35°方向走了80米到达B点,则∠AOB为( )
A.65° B.115° C.175° D.185°
7.点P是直线l外一点,A、B、C为直线l上三点,PA=4cm,PB=5cm,PC=2cm,则点P到直线l的距离是( )
A.2cm B.小于2cm C.不大于2cm D.4cm
二、填空题
8.计算:=____ 。
9.时钟表面5点30分时,时针与分针所夹角的度数是__________。
10.已知A、B是直线L外两点,则AB的垂直平分线与直线L的交点的个数是 。
11.已知x、y都是钝角的度数,甲、乙、丙、丁四人计算的结果依次为50°、
26°、72°、90°,你认为 结果是正确的。
12.乘火车从站出发,沿途经过3个车站可到达B站,那么在A、B两站之间最多共有________种不同的票价。
13.如图,在∠AOE的内部从O引出3条射线,那么图中共有_______个角;如果引出5条射线,有_______个角;如果引出条射线,有_______个角。
( http: / / www.21cnjy.com )
14.如图,将一副直角三角板叠在一起,使直角顶点重合于点O,则∠AOB+∠DOC=_______。
15.如图,已知矩形ABCD中,AB=2,BC=4,把矩形绕着一边旋转一周,则围成的几何体的体积为_____。
三、解答题
16.已知线段AD=8,平面上有一点P。
(1)若AP=5,PB等于多少时,点P在AB上?
(2)PB满足什么条件时,点P不在AB上?
(3)当PA=PB时,确定点P的位置;并比较PA+PB与AB的大小。
17.如图所示,AD=DB, E是BC的中点,BE=AC=2cm,线段DE的长,求线段DE。
① ② ③ ④ ⑤ ⑥
_
G
_
F
_
E
_
D
_
C
_
B
_
A
B
O
A
C
E
D
《4.1.1几何图形(1)》导学案NO:42
班级_______姓名_______小组_______小组评价_______教师评价_____
一、学习目标
1. 通过观察生活中的大量图片或实物,体验、感受、认识以生活中的事物为原型的几何图形,认识简单的几何体;
2.能由实物形状想象出几何图形,由几何图形想象出实物形状。
二、自主学习
1、请同学们阅读教材P116至P119第一行,完成下列填空:
(1)各种各样的物体,数学中只关注的是它们的 、 、
(2)有些几何图形的各部分不都在同一平面内,这样的几何图形叫做
(3)有些几何图形的各个部分都在同一平面内,这样的几何图形叫做
2、思考并回答下列各题:
(1)如图,下面是一些具体的物体与实物,试找出与立体图形类似的实物。
圣诞帽子 油桶 塔顶 西瓜
点拨:通过观察才能反映物体外观的主要特征,再抽象出具体的立体几何图形。
(2)下列几何体中(如图)属于棱锥的是( )
(1) (2) (3) (4) (5) (6)
A、①⑤ B、① C、①⑤⑥ D、⑤⑥
3、自学检测
(1)完成教材P119的练习;
(2)下面几种图形:①三角形;②长方形; ( http: / / www.21cnjy.com )③正方形;④圆;⑤圆锥;⑥圆柱。其中属于平面图形的是 ,属于立体图形的是
三、合作探究
1. 奥运会的标志是五环,每一个环的形状与 ( http: / / www.21cnjy.com )__类似;①电视机、②铅笔、③西瓜、④烟囱帽 ___与足球的形状类似;古埃及金字塔类似于几何体 。
2.月球、西瓜、易拉罐、篮球、热水瓶胆、书本等物体中,形状类似圆柱的有 个。
3.下列图形中,不是立体图形的是( )
A、球 B、圆 C、圆锥 D、圆柱
4.下列立体图形中,属于柱体的是( )
( http: / / www.21cnjy.com )
5.长方体属于( )A、棱锥 B、棱柱 C、圆柱 D、以上都不对
6.下列几何体中,不完全由平面围成的是( )
四、达标检测
1.完成教材P123的习题4.1第1、2题;
2.把下面几何体的标号写在相对应的括号里.
长方体有:{ } 棱柱体有:{ }
圆柱体有:{ } 球 体有:{ }
圆锥体有:{ }
五、拓展提高
由棱长是1cm 的若干个小正方体组成如图所示的几何体,那么这个几何体的表面积是( )
A、36cm B、33cm C、30cm D、27cm
分析:从不同的方向观察该几何体,想象图形的每一层
是由几个小正方体组成的,再由正方体的表面积公式计算。
《4.1.1几何图形(2)》导学案NO:43
班级_______姓名_______小组_______小组评价_______教师评价_____
一、学习目标
1. 经历从不同方向观察物体的活动过程,初步体会从不同方向观察同一物体可能看到不一样的结果;能作出一些简单物体的三视图;
2.了解多面体平面展开图,重点是正方体、圆锥、圆柱的平面展开图;能根据展开图初步判断和制作立体模型;
二、自主学习
1、请同学们阅读教材P119至P120,对 ( http: / / www.21cnjy.com )于一些立体图形的问题,我们通常把它们转化为平面图形来研究和处理。从不同方向看立体图形,往往会得到不同形状的平面图形。我们通常从三个方面看,即 、 、 。有些立体图形是由一些平面图形围成的,将它们的表面适当剪开,可以展开成 。这样的 称为相应立体图形的展开图。
2、请同学们对这个部分的两个探究进行动手操作,通过实际观察体会对立体图形的三视图及展开图。
3、自学检测
(1)完成教材P120的练习1、2题;
(2)如图所示,该物体从上往下看是( )
(3)下面六个正方形连在一起的图形,经折叠后能围成正方体的图形是 。
三、合作探究
1、从正面看、从左面看、从 ( http: / / www.21cnjy.com )上面看都一样的几何体是 、 ;从上面看一个几何体所形成的图形是圆,这个几何体可能是 。
2、如图是用4个长方体搭成的图形,从左面看,它应是下列图形中的( )
3、 如图,把左边的图形折叠起来,它会变为( )
( http: / / www.21cnjy.com )
4、如图,太阳在房子的后方,那么房子在地面上的影子是( )
5、观察右上图,这是由一些相同小正方体构成的立体图形的三种视图,构成这个立体图形的小正方体的个数是______
6.想一想,哪种几何体的表面展开成如下的平面图形,画出表示这些几何体的立体图形.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
四、达标检测
1、完成课本P124第3、4、5、6题;
2、一个几何体,是由许多规格相同的小正 ( http: / / www.21cnjy.com )方体堆积而成的,某主视图、左视图如图所示,要摆成这样的图形,至少需用________块正方体,最多需用_________正方体.
五、拓展提高
如图所示,一只昆虫要沿正方体表面从正方体的一个顶点A爬到相距它最远的另一个顶点,画出它爬行的最短路线?
《4.1.4点、线、面、体》导学案NO:44
班级_______姓名_______小组_______小组评价_______教师评价_____
一、学习目标
1. 探究点、线、面、体的几何特征,感受它们之间的关系;
2.感知正方体、圆锥、圆柱的展开图的特点。
二、自主学习
1、请同学们阅读教材P121至123第四行,完成下列填空:
(1)生活中有各种各样的立体图形,常见的几何体有 、 、 、
、 、 、球等。
(2)包围着体的是 。面有 和 两种。
(3)任何一个几何体都由 、 、 构成,平面是无限延伸的,面有平面和曲面,面面相交得 ,线线相交得 。点动成 ,线动成 ,面动成 。点、线、面、体都是几何图形。
2、自学检测:
(1)完成教材P122练习;
(2)笔尖在纸上划过就能写出汉字, ( http: / / www.21cnjy.com )这说明了______;汽车的雨刮器摆动就能刮去挡风玻璃上的雨滴,这说明了______;长方形纸片绕它的一边旋转形成了一个圆柱体,这说明了______.
(3)在下列几何体中,不能展开成平面图形的是( )
A、棱柱 B、圆柱 C、圆锥 D、球
三、合作探究
1. 按组成面的侧面“平”与“曲”划分,与圆柱为同一类的几何体是( )
A、圆锥 B、长方体 C、正方体 D、棱柱
2.圆锥的侧面展开图不可能是( )
A、小半个圆 B、半个圆 C、大半圆 D、圆
3.将下面的直角梯形绕直线l旋转一周,可以得到如下图所示的立体图形的是( )
4.下列说法错误的是( )
A、长方体、正方体都是棱柱 B、棱柱的侧棱长都相等 C、棱柱的侧面都是三角形
D、如果棱柱的底面各边长相等,那么它的各个侧面的面积一定相等
5.设长方体的顶点数为v,棱数为e,面数为f,则v+e+f等于( )
A、26 B、2 C、14 D、10
6.如图,说出下列各几何体的名称,哪些可以由平面图形的旋转得到
四、达标检测
1.三棱柱有______个顶点,______个面,______条棱,______条侧棱,______个侧面,侧面形状是______形,底面形状是______形.
2.直角三角形绕它最长边(即斜边)旋转一周得到的几何体为( )
3.如图,把第一行的图形绕虚线旋转一周便能形成第二行的某个几何体,请用线连起来.
五、拓展提高
有一个长为4cm、宽为3cm的长方形,分别绕它的长、宽所在直线旋转一周,得到不同的圆柱体,它们的体积分别是多大?
《4.2.1直线、射线、线段》导学案NO:45
班级_______姓名_______小组_______小组评价_______教师评价_____
一、学习目标
1.探究直线、射线、线段的联系和区别,掌握它们的表示方法;
2.理解两点确定一条直线的事实,并体会它在解决实际问题中的作用;
二、自主学习
1、请同学们自学教材P128至P129倒数第四行,并完成下列填空:
(1)直线、射线、线段的比较
直 线 射 线 线 段
相似处
端 点
延伸方向
图 形
表示法
注意:①线段、直线的表示与字母 无关;②射线的表示有方向性,
在前,射线上任意一点在后。
(2)直线:直线的公理 ( http: / / www.21cnjy.com ) (大声朗读三遍);点与直线的位置关系有两种:① ;②
2、自学检测:
(1)完成教材P129的练习题;
(2)要把木条固定在墙上至少要钉______个钉子,这是因为___________________;
(3)如图,点O在线段AB______;点B在射线AB______;
点A是线段AB的一个______.
三、合作探究
1.经过一点的直线有______条;经过两点的直线有______条,并且______一条。
2.把线段向一个方向延长,得到的是________;把线段向两个方向延长,得到的是______.
3.线段有______个端点,射线有______个端点,直线有______个端点.
4.如图,图中有______条射线,______条线段,
这些线段是_______ ___
5.如图,AC,BD交于点O,图中共有______条线段,
它们分别是____ __
6.如图,图中有____ ( http: / / www.21cnjy.com )__条线段,它们是______图中以A点为端点的射线有______条,它们是______图中有______条直线,它们是______
7.根据“反向延长线段CD”这句话,下图表示正确的是( )
8.如图所示,有直线、射线和线段,根据图中的特征判断其中能相交的是( )
四、达标检测
1.下列说法中正确的有( )
①钢笔可看作线段,②探照灯光线可看作射线,③笔直的高速公路可看作一条直线,
④电线杆可看作线段
(A)1个 (B)2个 (C)3个 (D)4个
2.下列说法中正确的语句共有( )
①直线AB与直线BA是同一条直线, ② ( http: / / www.21cnjy.com )线段AB与线段BA表示同一条线段,③射线AB与射线BA表示同一条射线,④延长射线AB至C,使AC=BC,⑤延长线段AB至C,使BC=AB,⑥直线总比线段长.
(A)2个 (B)3个 (C)4个 (D)5个
3.作图:
(1)点P在直线AB上,点M在直线AB外.
(2)直线AB、CD交于点O,点M在直线AB上,但不在CD上.
(3)经过点O的三条直线a,b,c.
五、拓展提高
看图写话
(1) ( http: / / www.21cnjy.com ) (2)
《4.1.1线段的大小比较》导学案NO:46
班级_______姓名_______小组_______小组评价_______教师评价_____
一、学习目标
1.结合图形认识线段间的数量关系,学会比较线段的大小;
2.理解两点之间线段最短的性质并能初步应用。知道两点之间的距离和线段中点的含义。
二、自主学习
1、请同学们自学教材P129至132第五行,并完成下列填空:
(1)仔细观察P129至P130中的图 ( http: / / www.21cnjy.com )形,比较两条线段的长短的方法有两种:(1)把它们放在同一条直线上比较,这种方法称为 法;2)用刻度尺去度量它们的长度进行比较,这种方法称为
(2)如图所示:点M把线段AB分成 ( http: / / www.21cnjy.com )相等的两条线段AM与BM,点M叫做线段AB的中点。这时AM=BM= AB,AB= AM= BM (默记)
(3)线段的性质:两点之间, 最短。(读三遍记忆)
(4)连接两点的线段的 ,叫做这两点之间距离。(读三遍)
2、典例解析
例、已知线段AB=14,在直线AB上有一点C,且BC=4,D是线段AC的中点,求线段AD的长。(请注意解题格式与步骤)
解:(1)当点C在线段AB上时(如图)
AC=AB-BC=14-4=10
D是AC的中点
AD=AC==5
(2)当点C在线段AB延长线上时(如图)
3、自学检测
(1)、完成教材P131练习;
(2)、已知A、B、C为直线上的三点,线段AB=9cm,BC=1cm,那A、C两点间的距离是( )
三、合作探究
1.若A、B、C、D为直线上顺次四点(如图所示),则AB+BD=AC+______;AC+BD=AD+____ __
2.若点C在线段AB的延长线上,则AC与AB的大小关系是______,并且AB+BC=______,AC-AB=______.
3.如图,A是直线BC外一点,请用不等号分别连接下列各式。
AB+AC______BC;AB+BC______AC;AC+BC______AB.
想一想:AB-AC________BC
4.已知线段OA=5cm,OB=3cm,则下列说法正确的是( )
A.AB=2cm B.AB=8cm
C.AB=4cm D.不能确定AB的长度
5.已知线段AB=10cm,AP+BP=20cm.下列说法正确的是( )
A.点P不能在直线AB上 B.点P只能在直线AB上
C.点P只能在线段AB的延长线上 D.点P不能在线段AB上
6.如图,延长线段AB到C,使D为AC的中点,DC=2,求AB的长.
四、达标检测
1.根据图形填空
(1)如图,若AB=BC=CD=DE,那么
①AE=______AB, ②AC=______AE,
③AD=______AE, ④CE=______AD.
(2)如图,已知D、E分别是线段AB、 BC的中点,
①若AB=3cm,BC=5cm,则DE=______cm;
②若AC=8cm,EC=3cm,则AD=______cm.
2.已知数轴上的三点A,B,C所对应的数 ( http: / / www.21cnjy.com )a,b,c满足a<b<c,abc<0和a+b+c=0,那么线段AB与BC的大小关系是( )
A.AB>BC B.AB=BC C.AB<BC D.不确定
3.已知C为线段AB的中点,AB=10cm,D是AB上一点,若CD=2cm,求BD的长.
五、拓展提高
12.已知C,D两点将线段AB分为三部分,且AC∶CD∶DB=2∶3∶4,若AB的中点为M,BD的中点为N,且MN=5cm,求AB的长.
《4.3.1角(1)》导学案NO:47
班级_______姓名_______小组_______小组评价_______教师评价_____
一、学习目标
1.掌握角的两种定义形式和四种表示方法;
2.通过在图片、实例中找角,体会角在实际生活中的应用。
二、自主学习
1、请同学们自学教材P 136,并完成下列填空:
(1)①____________的图 ( http: / / www.21cnjy.com )形叫做角,____________________叫做角的顶点,_____________________叫做角的边.(读三遍)
②角也可以看作是由一条_________绕着它的__________而形成的图形,这条射线的起始位置叫做角的______,其终止位置叫做角的________.(读三遍)
(2)角的表示法
①用一个数字,如; ②用一个大写字母,
如;(在角的顶点有几个角时不能用一个大写字母表示)
③用三个大写字母,如∠ABC;(顶点的字母写在中间)
④用一个希腊字母,如。
(3)一条射线绕其端点O按逆时 ( http: / / www.21cnjy.com )针方向旋转得到∠AOB,当角的终边OB旋转到与角的始边OA成一条直线时,称∠AOB为______;若角的终边继续旋转,当角的终边OB与角的始边OA重合时,称∠AOB为______.
2、自学检测:完成教材P138练习第1题及P143习题4.3第1、2题。
三、合作探究
1.下列说法正确的是( )
A、一个周角就是一条射线 B、平角是一条直线
C、角的两边越长,角就越大 D、∠AOB也可以表示为∠B
2.下列4个图形中,能用∠1、∠AOB、∠O三种方法表示同一角的图形是( )
3.如图所示,点O在直线AB上,图中小于180°的角
共有( ).
A、7个 B、8个 C、9个 D、10个
4.如图,(1)中有______个角,(2)中有______个角;(3)中
有______个角.以此类推,若一个角内有n条射线,则可有______个角.
5.如图,图中能用一个大写字母表示的角有 个。分别把它们表示出来________________________
四、达标检测
1.下列关于角的说法正确的个数是( )
①角是由两条射线组成的图形;②角的边越长,角越大; ③在角一边延长线取一点; ④角可以看作由一条射线绕着它的端点旋转而形成的图形.
A、1个 B、2个 C、3个 D、4个
2.图中共有______个小于平角的角,它们分别是_______________其
中以D为顶点的小于平角的角有______个.
3.图中以OC为边的角有______个,它们分别是______
五、拓展提高
2.用三个字母表示图中所注的∠1、∠2、∠3、∠4:
(1) (2)
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(1)∠1是______;∠2是______;∠3是______;
(2)∠1是______;∠2是______;∠3是______; ∠4是______.
《4.3.1角(2)》导学案NO:48
班级_______姓名_______小组_______小组评价_______教师评价_____
一、学习目标
1.掌握角度的换算关系;
2.能进行角的简单的加、减、乘、除运算。
二、自主学习
1、请同学们自学教材P137,并完成下列填空:
以度、分、秒为单位的角度制规定,把一个 ( http: / / www.21cnjy.com )周角______,每一份叫做1度,记作______;把1度的角______,每一份叫做1分,记作______;把1分的角______,每一份叫做1秒,记作______.这样1周角是______°,1平角是______°,1°=______',1′=______″.
2、典例解析
例1.下列算式正确的是( )
① ② ③
④ A ①和② B①和③ C②和③ D②和④
思路分析:角度的换算只要注意度化分乘以60,分化秒乘以60;分化度除以60,秒化分除以60 ;
例2.计算(1)49°38′+66°22′ (2)180°-79°19′
(3)22°16′×5 (4)182°36′÷4.
3、自学检测
完成教材P138第2、3题及P143第3题。
三、合作探究
1.将一个周角分成360份,其中每一份是_____°的角,直角等于____°,平角等于______°
2.计算
(1)0.4°=______' (2)0.6′=______″
(3)24′=______° (4)12″=______′
(5)57.32°=______°______′______″
(6)17°14′24″=______°
(7)17°40′÷3=______°______′______″
(8)25°36′18″×6=______°______′______″
3.若,则、、( )
A 都是锐角 B 都是钝角 C 两个锐角,一个钝角 D 至少有两个锐角
4.两个锐角相加一定是( )
A 锐角 B 钝角 C 直角 D以上均有可能
5.计算:(2)180°—79°19′ (3)22°16′×5
6.时钟的时针1小时旋转多少度 时钟的分针1分钟旋转多少度 2点整时,时钟的时针与分针之间的夹角是多少度 3点呢?
四、达标检测
1. 直角= 平角= 周角。
2.若,则( )
A B C D 以上都不对
3. 计算
(1)49°38′+66°22′ (2)182°36′÷4 (3)32°16′25″×4-78°25′
五、拓展提高
时钟在8:30时,时针与分针的夹角为多少度 从6时到7时,钟表面上的时针与分针何时成的角?
《4.3.2角的比较与运算》导学案NO:49
班级_______姓名_______小组_______小组评价_______教师评价_____
一、学习目标
1.了解角度的比较方法,掌握角度的和差倍分关系。
2.掌握角平分线的定义和性质,能运用角平分线解决简单的角度问题。
二、自主学习
请同学们自学教材P138至P140,完成下列填空:
1、角的比较:①与线段长短的比较相类似,比较两个角的大小有2种方法:
方法一为:_________________________;方法二为:__________________________
②思考:在上右图中共有几个角,怎么数的?
在图中表示出来。
在右图中,
∠AOB=_________+____________
∠BOC=________________-__________
2、角的平分线
(1)、如图,如果∠AOC=∠BOC,那么射线OC是∠AOB的角平分线。
角平分线的定义:_______________________________________________(读三遍)
符号语言:∵OC平分∠AOB
∴∠AOC=∠BOC
(∠AOB=2∠ 或∠AOB =2∠ ;
或∠AOC=∠ ,∠BOC =∠_____ )
(2)、请画出下面两个角的角平分线,
3、例题示范
例、O是直线AB上一点,
∠AOC=53°,OD平分∠BOC,
求∠BOD的度数?(请注意解题格式与步骤)
4、自学检测
完成教材P140至P141练习。
三、合作探究
1、如下图,用“=”或“>”或“<”填空
(1)∠AOC_______∠AOB+∠BOC
(2)∠AOC_______∠AOB
(3)∠BOD-∠BOC______∠DOC
(4)∠AOD______∠AOC+∠BOD
2、如图,OB是平角∠AOC的角平分线,OD平分∠BOC,求∠AOD的度数。
3、如图,OB是∠AOC的平分线,OD是∠COE的平分线。
⑴如果∠AOB=40°,∠DOE=30°,那么∠BOD是多少度?
⑵如果∠AOE=140°,∠COD=30°,那么∠AOB是多少度?
四、达标检测
1.在小于平角的∠AOB的内部取一点C,并作射线OC,则一定存在( ).
(A)∠AOC>∠BOC (B)∠AOC=∠BOC
(C)∠AOB>∠AOC (D)∠BOC>∠AOC
2.按图填空:
(1)∠ABC是∠ABD与∠DBC的_____;(2)∠BDC是∠ADC与∠ADB的______.
(3)如果BD平分∠ABC,则∠ABD=________= ____ ∠ABC。
五、拓展提高
如图,∠AOB=90°,∠BOC=30°,OM平分∠AOB,ON平分∠BOC,
⑴求∠MON的度数,
⑵若∠AOB=∠α,若∠BOC=∠β(∠β为锐角)其他条件不变,求∠MON的度数。(用含α、β的式子表示)
⑶探究:从⑴⑵中你发现有什么规律?
《4.3.3余角和补角》导学案NO:50
班级_______姓名_______小组_______小组评价_______教师评价_____
一、学习目标
1.认识一个角的余角和补角,探究余角和补角的性质;
2.了解方位角,能确定具体物体的方位,学会简单的逻辑推理。并能对问题的结论
二、自主学习
1、请同学们自学P141至P143第四行,并完成下列填空与探究:
(1)①如果两个角的和是 ,那么这两个角叫做互为余角,其中一个角是另一个角的余角。即∠1是∠2的余角或∠2是∠1的余角。
②如果两个角的和是 ,那么这两个角叫做互为补角,其中一个角是另一个角的补角。即∠3是∠4的补角或∠4是∠3的补角。
(2)探究余角的性质:如右下图∠1 与∠2互余,
∠3 与∠4互余 ,如果∠1=∠3,那么∠2与∠4相等吗,为什么?
(3)探究补角的性质
请同学们自已作图探究,∠1 与∠2互补,∠3 与∠4互补 ,如果∠1=∠3,那么∠2与∠4相等吗,为什么?(对余角和补角的性质读三遍)
2、例题解析
例1、若一个角的补角等于它的余角4倍,求这个角的度数。
解: 设这个角是x °,则它的补角是( ),余角是( ) 。
根据题意得:
( )= 4 ( )
解之得: x =( )
答:这个角的度数是 。
例2、如图,∠AOB=90°,∠COD=∠ ( http: / / www.21cnjy.com )EOD=90°,C,O,E在一条直线上,且∠2=∠4,请说出∠1与∠3之间的关系?并试着说明理由?
3、自学检测:完成P141练习及P144第8、9题。
三、合作探究
1. 一个角的补角是它的3倍,这个角是
2. 如图∠AOB = 90 °,∠COD = 90 °,则∠1 ∠2.
3.A看B的方向是北偏东21°,那么B看A的方向( )
A、南偏东69° B、南偏西69° C、南偏东21° D、南偏西21°
4.如图,下列说法中错误的是( )
A、OC的方向是北偏东60° B、 OC的方向是南偏东60°
C、OB的方向是西南方向 D、 OA的方向是北偏西22°
5.如图.货轮O在航行过程中 ( http: / / www.21cnjy.com ),发现灯塔A在它南偏东60°的方向上,同时在它北偏东40°,南偏西10°,西北(即北偏西45°)方向上又分别发现了客轮B,货轮C和海岛D.仿照表示灯塔方位的方法画出表示客轮B,货轮C和海岛D方向的射线.
四、达标检测
1.70°的余角是 ,补角是 。
∠(∠ 90°)的它的余角是 ,它的补角是 。
2.在点O 北偏西60°的某处有一点A,在点O南偏西20°的某处有一点B,则
∠AOB的度数是( )A、100° B、70° C、180° D、140°
3.(1)一个角的余角为54°求这个角的补角的度数.
(2)两个角的比是7∶3,它们的差是72°,求这两个角的度数.
五、拓展提高
已知∠ 的余角是∠ 的补角的并且求∠ +∠ 的值.
《图形认识初步》复习学案NO:51
班级_______姓名_______小组_______小组评价_______教师评价_____
一、知识点回顾
(一)多姿多彩的图形
立体图形:棱柱、棱锥、圆柱、圆锥、球等。
1、几何图形
平面图形:三角形、四边形、圆等。
主(正)视图---------从正面看
2、几何体的三视图 侧(左、右)视图-----从左(右)边看
俯视图---------------从上面看
3、立体图形的平面展开图
(1)同一个立体图形按不同的方式展开,得到的平现图形不一样的。
(2)了解直棱柱、圆柱、圆锥的平面展开图,能根据展开图判断和制作立体模型。
4、点、线、面、体
(1)几何图形的组成:点、线、面、体。
(2)点动成线,线动成面,面动成体。
(二)直线、射线、线段
1、基本概念(请同学们从它们的图形、端点个数、表示法、作法叙述、延长叙述这五个方面列表比较)
2、直线的性质:两点确定一条直线。
3、画一条线段等于已知线段:(1)度量法 (2)用尺规作图法
4、线段的大小比较方法 :(1)度量法 (2)叠合法
5、线段的中点(二等分点):定义:把一条线段平均分成两条相等线段的点。
图形:
A M B
符号:若点M是线段AB的中点,则AM=BM=AB,AB=2AM=2BM。
6、线段的性质:两点之间,线段最短。
7、两点的距离:连接两点的线段长度叫做两点的距离。
8、点与直线的位置关系:(1)点在直线上 (2)点在直线外。
(三)角
1、角:由公共端点的两条射线所组成的图形叫做角。
2、角的表示法(四种):
3、角的度量单位及换算
4、角的分类:锐角、直角、钝角、平角、周角
5、角的比较方法:(1)度量法 (2)叠合法
6、角的和、差、倍、分及其近似值
7、画一个角等于已知角
8、角的平线线
定义:从一个角的顶点出发,把这个角分成相等的两个角的射线叫做角的平分线。
图形: 符号:
9、互余、互补的概念及性质
10方向角:正方向、北(南)偏东(西)方向、东(西)偏北(南)方向
二、巩固练习
1、计算:30.26°=____ °____′____″; 18°15′36″ =____ __ °;
36°56′+18°14′=____ ; 108°- 56°23′ =________;
27°17′×5 =____ ; 15°20′÷6 =____ (精确到分)
2、下列说法中正确的是( )
A、延长射线OP B、延长直线CD
C、延长线段CD D、反向延长直线CD
3、下面是我们制作的正方体的展开图,每个平面内都标注了字母,请根据要求回答问题:
(1)和面A所对的会是哪一面?
(2)和B面所对的会是哪一面?
(3)面E会和哪些面相交?
4、已知平面内有四个点A、B、C、D,过其中任意两点画直线,最少可画多少条直线,最多可画多少条直线?画出图来.
5、已知点B是线段AD的中点,点C是线段BD的中点,CD=2.5厘米,请你求出线段AB、AC、AD、BD的长各为多少?
6、已知线段AB=4厘米,延长AB到C,使B C=2AB,取AC的中点P,求PB的长.
7、如图,∠AOB是直角,OD平分∠BOC,OE平分∠AOC,求∠EOD的度数。(10分)
《图形认识初步》训练学案NO:52
班级_______姓名_______小组_______小组评价_______教师评价_____
一、选择题
1.如图,下列图形中,不是正方体展开图的是( )
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
A B C D
2.正方体的截面不可能构成的平面图形是( )
A.矩形 B.六边形 C.三角形 D.七边形
3.如果两个角互为补角,而其中一个角比另一个角的4倍少30°,那么这两个角是( )
A.42°,138°或40°,130°; B.42°,138°;
C.30°,150°; D.以上答案都不对
4. 已知点A、B、C都是直线l上的点,且AB=5cm,BC=3cm,那么点A与点C之间的距离是( )
A.8cm B.2cm或6cm C.8cm或2cm D.4cm
5. 下列图形中,能够相交的是 ( )
6.甲从O点出发,沿北偏西30°走了50米到达A点,乙也从O点出发,沿南偏东35°方向走了80米到达B点,则∠AOB为( )
A.65° B.115° C.175° D.185°
7.点P是直线l外一点,A、B、C为直线l上三点,PA=4cm,PB=5cm,PC=2cm,则点P到直线l的距离是( )
A.2cm B.小于2cm C.不大于2cm D.4cm
二、填空题
8.计算:=____ 。
9.时钟表面5点30分时,时针与分针所夹角的度数是__________。
10.已知A、B是直线L外两点,则AB的垂直平分线与直线L的交点的个数是 。
11.已知x、y都是钝角的度数,甲、乙、丙、丁四人计算的结果依次为50°、
26°、72°、90°,你认为 结果是正确的。
12.乘火车从站出发,沿途经过3个车站可到达B站,那么在A、B两站之间最多共有________种不同的票价。
13.如图,在∠AOE的内部从O引出3条射线,那么图中共有_______个角;如果引出5条射线,有_______个角;如果引出条射线,有_______个角。
( http: / / www.21cnjy.com )
14.如图,将一副直角三角板叠在一起,使直角顶点重合于点O,则∠AOB+∠DOC=_______。
15.如图,已知矩形ABCD中,AB=2,BC=4,把矩形绕着一边旋转一周,则围成的几何体的体积为_____。
三、解答题
16.已知线段AD=8,平面上有一点P。
(1)若AP=5,PB等于多少时,点P在AB上?
(2)PB满足什么条件时,点P不在AB上?
(3)当PA=PB时,确定点P的位置;并比较PA+PB与AB的大小。
17.如图所示,AD=DB, E是BC的中点,BE=AC=2cm,线段DE的长,求线段DE。
① ② ③ ④ ⑤ ⑥
_
G
_
F
_
E
_
D
_
C
_
B
_
A
B
O
A
C
E
D
