人教版数学六年级下册6 整理和复习(2.图形与几何)课件(66张ppt)
文档属性
| 名称 | 人教版数学六年级下册6 整理和复习(2.图形与几何)课件(66张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-13 08:45:41 | ||
图片预览









文档简介
(共66张PPT)
6 整理和复习
数学配人教版
(六年级/下册)
第1课时 平面图形的认识与测量
第2课时 平面图形的周长与面积
第3课时 立体图形
第4课时 练习十八
第5课时 图形的运动
第6课时 练习十九
第7课时 图形与位置
第8课时 练习二十
2. 图形与几何
1.填空题。
(1)过直线外一点能画( )条直线与已知直线垂直,能画( )条直线与已知直线平行。
第1课时 平面图形的认识与测量
1
1
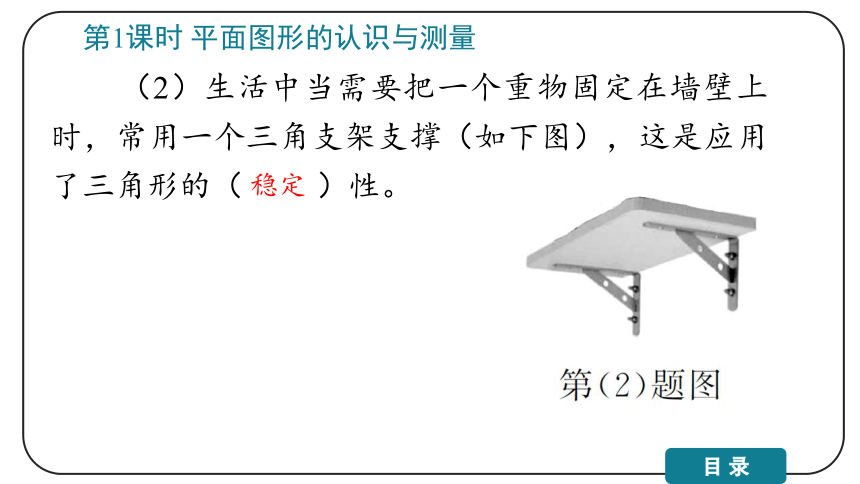
(2)生活中当需要把一个重物固定在墙壁上时,常用一个三角支架支撑(如下图),这是应用了三角形的( )性。
第1课时 平面图形的认识与测量
稳定
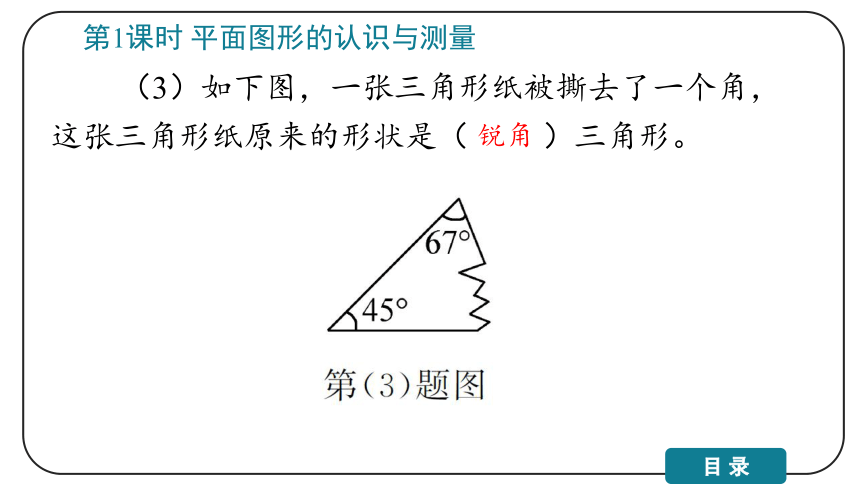
(3)如下图,一张三角形纸被撕去了一个角,这张三角形纸原来的形状是( )三角形。
第1课时 平面图形的认识与测量
锐角
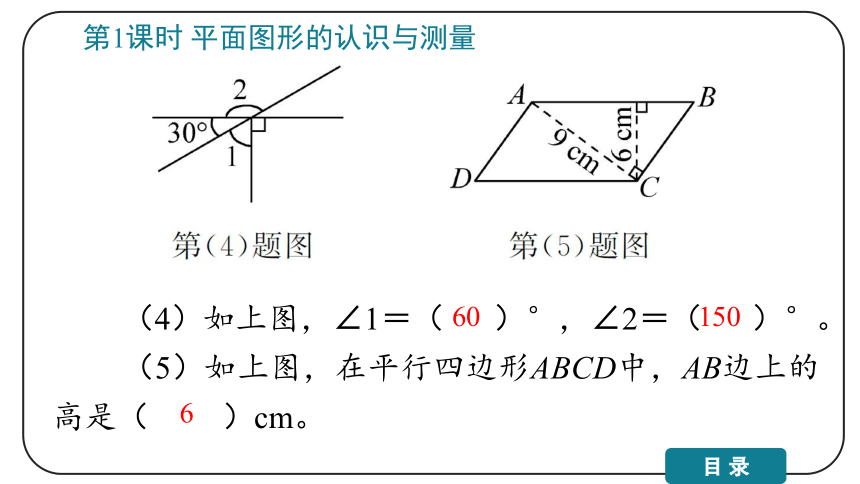
(4)如上图,∠1=( )°,∠2=( )°。
(5)如上图,在平行四边形ABCD中,AB边上的高是( )cm。
第1课时 平面图形的认识与测量
60
150
6
(6)有四条线段,长度分别为4 cm、8 cm、10 cm、12 cm,选其中三条组成三角形,可以组成( )个不同的三角形。
第1课时 平面图形的认识与测量
3
2.选择题。(把正确答案的序号填在括号里)
(1)画一条长14 cm的( )。
(A)直线
(B)射线
(C)线段
第1课时 平面图形的认识与测量
C
(2)一个圆形纸片的半径是4.2 cm,它的直径是( )cm。
(A)8.4
(B)2.1
(C)16.8
第1课时 平面图形的认识与测量
A
(3)用一副三角板可以拼成的角的度数是( )。
(A)160°
(B)135°
(C)65°
第1课时 平面图形的认识与测量
B
(4)两个( )一定能拼成一个平行四边形。
(A)等底等高的三角形
(B)等腰三角形
(C)完全一样的三角形
第1课时 平面图形的认识与测量
C
3.判断题。(对的画“√”,错的画“×”)
(1)如果两条直线都和第三条直线平行,那么这两条直线一定也互相平行。 ( )
(2)两条平行线之间可以画出无数条垂线段,这些垂线段的长度都相等。 ( )
(3)两端都在圆上的线段是圆的直径。
( )
第1课时 平面图形的认识与测量
√
√
×
(4)用一个放大倍率是5倍的放大镜看一个15°的角,看到的角的度数是75°。( )
(5)两个锐角的和一定是钝角。( )
第1课时 平面图形的认识与测量
×
×
4.根据下图回答问题。
(1)图中三角形的两条直角边的长分别是多少?
7÷2=3.5(cm)
6cm
第1课时 平面图形的认识与测量
(2)长方形的长、宽分别是多少?
第1课时 平面图形的认识与测量
长:7cm
宽:3.5cm
(3)梯形的上底、下底、高分别是多少?
第1课时 平面图形的认识与测量
上底:7cm
下底:7+6=13(cm)
高:3.5cm
5.如下图,要想从A、B两点各修一条小路与公路连接,怎样修能使这两条小路最短?请在图上画出来。
第1课时 平面图形的认识与测量
6.如下图,将长方形折起来后得到∠2。已知∠2=70°,求∠1的度数。
∠1=180°-2∠2=40°
第1课时 平面图形的认识与测量
7.一个等腰三角形,如果其中一个内角是50°,那么另外两个内角分别是多少度?
锦囊妙计 分两种情况考虑,50°的角可能是顶角也可能是底角。
情况一:顶角是50°,(180°-50°)÷2=65°,另外两个内角都是65°。
情况二:一个底角是50°,180°-50°×2=80°,另外两个内角分别是50°、80°。
第1课时 平面图形的认识与测量
1.填空题。
(1)如右图,如果平行四边形的面积是8 m2,那么圆的面积是( )m2。
第2课时 平面图形的周长与面积
12.56
136
(2)一个平行四边形和一个三角形等底等高。已知三角形的面积是68 dm2,则平行四边形的面积是( )dm2。
(3)一张长是10 cm、宽是7 cm的长方形纸,最多能剪( )个直径是2 cm的圆片。
(4)估计下图的面积约为( )cm2。(每格的面积是1 cm2)
第2课时 平面图形的周长与面积
15
答案不唯一
50
2.在方格纸上分别画一个三角形和一个梯形,使它们都与图中平行四边形的面积相等。
第2课时 平面图形的周长与面积
答案不唯一
3.计算下面各图形的周长和面积。(单位:cm)
第2课时 平面图形的周长与面积
8+6+10=24(cm)
8×6÷2=24(cm2)
3.计算下面各图形的周长和面积。(单位:cm)
第2课时 平面图形的周长与面积
3.14×20÷2+18×2+20=87.4(cm),
20×16+3.14×(20÷2)2÷2=477(cm2)
4.如下图,明明的妈妈在自己家的院墙边用篱笆围了一个牛栏,篱笆全长20.5 m,牛栏的占地面积是多少平方米?
(20.5-8.5)×8.5÷2=51(m2)
第2课时 平面图形的周长与面积
5.小明沿着一个圆形水池的外沿走了一周,正好走了50步,每步的距离约是0.628 m。这个水池的占地面积约是多少平方米?
0.628×50=31.4(m)
3.14×(31.4÷3.14÷2)2=78.5(m2)
第2课时 平面图形的周长与面积
6.如下图所示,梯形的上底是18 cm,下底是34 cm,阴影部分的面积是510 cm2。这个梯形的面积是多少平方厘米?
510×2÷34=30(cm)
(18+34)×30÷2=780(cm2)
第2课时 平面图形的周长与面积
7.胡伯伯在超市买了4瓶啤酒,售货员将4瓶啤酒捆扎在一起,捆扎方法如下图所示。照这样捆3圈至少用绳子多少厘米?(接头处不计)
(3.14×6+4×6)×3=128.52(cm)
第2课时 平面图形的周长与面积
8.如下图所示,正方形的面积是60 cm2,空白部分的面积是多少平方厘米?
锦囊妙计 圆的半径的平方等于正方形的面积。
第2课时 平面图形的周长与面积
1.填空题。
(1)小明用正方体木块摆成一个立体图形,从三个不同方位看到的形状如下图。摆这个立体图形至少用( )个小正方体,最多用( )个小正方体。
第3课时 立体图形
13
15
(2)一个圆柱的底面周长是25.12 cm,高是8 cm,它的侧面积是( )cm2,它的体积是( )cm3。
(3)一个长方体的底面积是0.4 m2,高是6 dm,它的体积是( )dm3。
(4)一个圆柱形容器中盛满14.13 L水,用这些水倒满一个与它等底等高的圆锥形容器,圆柱形容器中还剩( )L水。
第3课时 立体图形
200.96
401.92
240
9.42
第3课时 立体图形
2.判断题。(对的画“√”,错的画“×”)
(1)表面积相等的两个长方体,它们的体积一定相等。 ( )
(2)用同一张长方形硬纸,可以卷成两个不同的圆柱,它们的体积相等。 ( )
(3)把一个圆柱削成一个最大的圆锥,这个
圆锥的体积是这个圆柱体积的 ( )
×
×
√
3.求下面图形的体积。(单位:dm)
第3课时 立体图形
3.求下面图形的体积。(单位:dm)
第3课时 立体图形
3.14×[(6÷2)2-(4÷2)2]×8=125.6(dm3)
4.一个长方体正好可以切成5个同样大小的正方体,切成的5个正方体的表面积之和比原来长方体的表面积增加了200 cm2。原来长方体的表面积是多少平方厘米?
200÷8=25(cm2)
(5×4+2)×25=550(cm2)
第3课时 立体图形
5.一个棱长是4 dm的正方体容器装满水后,将这些水倒入一个底面积是12 dm2的圆锥形容器里正好装满,这个圆锥形容器的高是多少分米?(容器厚度不计)
第3课时 立体图形
6.一辆货车车厢是一个长方体,它的长是4 m,宽是1.5 m,高是4 dm。如果装满一车沙子,卸后将沙子堆成一个高是5 dm的圆锥,那么这个圆锥的底面积是多少平方米?
第3课时 立体图形
1.填空题。
(1)在括号里填上合适的数或单位。
0.15时=( )分
3500平方米=( )公顷
一瓶果汁的体积大约是300( )。
一个苹果的质量大约是200( )。
第4课时 练习十八
9
0.35
mL
g
第4课时 练习十八
(2)观察 下面这些图分别
是从哪个方向看到的?
左面
上面
前面
2.求阴影部分的面积。
第4课时 练习十八
2.求阴影部分的面积。
第4课时 练习十八
3.如下图所示,一个箱子的下半部分是长方体,这个长方体的长是40 cm,宽是30 cm,高是20 cm,上半部分是圆柱的一半。求这个箱子的表面积和体积。
第4课时 练习十八
第4课时 练习十八
第4课时 练习十八
4.右图所示的立体图形是由棱长为2 cm的小正方体搭成的,所有的表面都涂色。其中,只有1个面涂色的小正方体有( )个;只有2个面涂色的小正方体有( )个;只有3个面涂色的小正方体有( )个;只有4个面涂色的小正方体有( )个;只有5个面涂色的小正方体有( )个。该立体图形的表面积是( )cm2。
锦囊妙计 与其他的小正方体有n个面重合的小正方体,需要涂色的只有(6-n)个面。
第4课时 练习十八
第4课时 练习十八
4.右图所示的立体图形是由棱长为2 cm的小正方体搭成的,所有的表面都涂色。其中,只有1个面涂色的小正方体有( )个;只有2个面涂色的小正方体有( )个;只有3个面涂色的小正方体有( )个;只有4个面涂色的小正方体有( )个;只有5个面涂色的小正方体有( )个。该立体图形的表面积是( )cm2。
1
0
1
4
2
120
5.施工队用混凝土浇筑成一个无盖的长方体水槽(如下图),从外面量长是10 dm,宽是6 dm,高是5 dm。混凝土厚1 dm。
(1)请计算这个水槽的容积。
(10-1×2)×(6-1×2)×(5-1)=128(dm3)
第4课时 练习十八
(2)若给水槽的里面、外面均贴上瓷砖(水槽的外底面不贴),则贴瓷砖的面积是多少?
(10×5+6×5)×2+(10-1×2)×(5-1)×2+(6-1×2)×(5-1)×2+(10-1×2)×(6-1×2)=288(dm2)
288+10×6-(10-1×2)×(6-1×2)=316(dm2)
第4课时 练习十八
1.选择题。(把正确答案的序号填在括号里
(1)下列图形中,对称轴最多的是( )。
第5课时 图形的运动
B
(2) 观察下图,图①( )得到图②。
(A)先绕点O顺时针旋转90°,再向右平移10格
(B)先绕点O逆时针旋转90°,再向右平移10格
(C)先绕点O顺时针旋转90°,再向右平移8格
第5课时 图形的运动
B
第5课时 图形的运动
2.按要求画出图形。
(1)按对称轴将图①补完整。
(2)将(1)中补完整的图①向右平移9格,得到图②。
(3)把图②左下角的顶点记为点O,将图②绕点O逆时针旋转90°,得到图③。
(4)将图③按1∶2缩小,得到图④。
(图④位置不唯一 )
3.一个长是12 cm、宽是9 cm的长方形按1∶3缩小后,缩小的长方形的面积与原长方形的面积的比是( ),缩小的长方形的周长是原长方形周长
的
第5课时 图形的运动
1∶9
1
3
锦囊妙计 把一个长方形按1∶3缩小就是把这
个长方形的长和宽缩小到原来的
1.下面哪些图形是轴对称图形?画出它们所有的对称轴。
第6课时 练习十九
第1、2、4个图形是轴对称图形。
2.下面5个图形的阴影部分面积相等吗?为什么?
它们阴影部分的面积( )。因为图②③④⑤中的各部分图案经过平移和( )后都能变成图( )。
第6课时 练习十九
相等
旋转
①
3.(1)将图①向右平移3格后得到图②;以直线a为对称轴,作图②的轴对称图形,得到图③。
(2)画出三角形绕点O逆时针旋转90°后的图形。
(3)画出长方形按2∶1放大后的图形。
第6课时 练习十九
4.你能利用平移和旋转的方法,将图2恢复到图1的样子吗?请你把“恢复”的过程写下来。
第6课时 练习十九
锦囊妙计 根据平移和旋转的特点结合图1和图2来比较分析。
图2中的左下角图形先向上平移2格,再向右平移2格。右下角的图形先向左平移2格,再绕该图形的左上角顶点逆时针旋转90°。
第6课时 练习十九
1.以学校为观测点。
(1)公园在学校的( )偏( )( )°方向( )m处。
(2)体育场在学校的( )方向( )m处。
(3)农贸市场在学校的( )偏( )( )°方向( )m处。
第7课时 图形与位置
北
东
50
500
正北
200
南
西
35
400
2.在游乐场示意图已标出的位置上写出各个项目的名称,并填空。
第7课时 图形与位置
5,4
(1)大门位于点(0,1),向东走200 m到达旋转木马。
(2)碰碰车位于点( ),在旋转木马的北偏( )( )°方向上。
东
45
(3)云霄飞车位于点(3,6),在碰碰车的( )偏( )( )°方向上。
(4)摩天轮到旋转木马和云霄飞车的距离相等,它位于点( )。
第7课时 图形与位置
北
西
45
5,3
(5)山洞飞车位于点(7,7),向西走600 m到达激流勇进;秋千与这两处距离相等,它位于点( )。
第7课时 图形与位置
4,8
3.量一量,画一画。
(1)轮船在灯塔的北偏( )( )°方向( )m处。
第7课时 图形与位置
西
60
400
第8课时 练习二十
1.彤彤一家到公园玩。
(1)公园大门的位置是( ),动物园的位置是( ),荷花池的位置是( )。( )的位置是(8,5)。
4,6
8,8
12,6
餐厅
第8课时 练习二十
(2)游乐场的位置是(5,2),请在图中标出来。
方向 路程/米 时间/分钟
王老师家→博物馆 8
博物馆→小伟家 11
小伟家→博物馆 9
博物馆→王老师家 7
2.周末,王老师去小伟家家访。
第8课时 练习二十
北偏东65°
450
南偏东55°
600
北偏西55°
600
南偏西65°
450
(1)根据路线图,说一说王老师去小伟家家访和回来时所走的方向和路程,并完成下表。
(2)王老师走完全程的平均速度是多少?
锦囊妙计 用总路程除以总时间。
第8课时 练习二十
60米/分
6 整理和复习
数学配人教版
(六年级/下册)
第1课时 平面图形的认识与测量
第2课时 平面图形的周长与面积
第3课时 立体图形
第4课时 练习十八
第5课时 图形的运动
第6课时 练习十九
第7课时 图形与位置
第8课时 练习二十
2. 图形与几何
1.填空题。
(1)过直线外一点能画( )条直线与已知直线垂直,能画( )条直线与已知直线平行。
第1课时 平面图形的认识与测量
1
1
(2)生活中当需要把一个重物固定在墙壁上时,常用一个三角支架支撑(如下图),这是应用了三角形的( )性。
第1课时 平面图形的认识与测量
稳定
(3)如下图,一张三角形纸被撕去了一个角,这张三角形纸原来的形状是( )三角形。
第1课时 平面图形的认识与测量
锐角
(4)如上图,∠1=( )°,∠2=( )°。
(5)如上图,在平行四边形ABCD中,AB边上的高是( )cm。
第1课时 平面图形的认识与测量
60
150
6
(6)有四条线段,长度分别为4 cm、8 cm、10 cm、12 cm,选其中三条组成三角形,可以组成( )个不同的三角形。
第1课时 平面图形的认识与测量
3
2.选择题。(把正确答案的序号填在括号里)
(1)画一条长14 cm的( )。
(A)直线
(B)射线
(C)线段
第1课时 平面图形的认识与测量
C
(2)一个圆形纸片的半径是4.2 cm,它的直径是( )cm。
(A)8.4
(B)2.1
(C)16.8
第1课时 平面图形的认识与测量
A
(3)用一副三角板可以拼成的角的度数是( )。
(A)160°
(B)135°
(C)65°
第1课时 平面图形的认识与测量
B
(4)两个( )一定能拼成一个平行四边形。
(A)等底等高的三角形
(B)等腰三角形
(C)完全一样的三角形
第1课时 平面图形的认识与测量
C
3.判断题。(对的画“√”,错的画“×”)
(1)如果两条直线都和第三条直线平行,那么这两条直线一定也互相平行。 ( )
(2)两条平行线之间可以画出无数条垂线段,这些垂线段的长度都相等。 ( )
(3)两端都在圆上的线段是圆的直径。
( )
第1课时 平面图形的认识与测量
√
√
×
(4)用一个放大倍率是5倍的放大镜看一个15°的角,看到的角的度数是75°。( )
(5)两个锐角的和一定是钝角。( )
第1课时 平面图形的认识与测量
×
×
4.根据下图回答问题。
(1)图中三角形的两条直角边的长分别是多少?
7÷2=3.5(cm)
6cm
第1课时 平面图形的认识与测量
(2)长方形的长、宽分别是多少?
第1课时 平面图形的认识与测量
长:7cm
宽:3.5cm
(3)梯形的上底、下底、高分别是多少?
第1课时 平面图形的认识与测量
上底:7cm
下底:7+6=13(cm)
高:3.5cm
5.如下图,要想从A、B两点各修一条小路与公路连接,怎样修能使这两条小路最短?请在图上画出来。
第1课时 平面图形的认识与测量
6.如下图,将长方形折起来后得到∠2。已知∠2=70°,求∠1的度数。
∠1=180°-2∠2=40°
第1课时 平面图形的认识与测量
7.一个等腰三角形,如果其中一个内角是50°,那么另外两个内角分别是多少度?
锦囊妙计 分两种情况考虑,50°的角可能是顶角也可能是底角。
情况一:顶角是50°,(180°-50°)÷2=65°,另外两个内角都是65°。
情况二:一个底角是50°,180°-50°×2=80°,另外两个内角分别是50°、80°。
第1课时 平面图形的认识与测量
1.填空题。
(1)如右图,如果平行四边形的面积是8 m2,那么圆的面积是( )m2。
第2课时 平面图形的周长与面积
12.56
136
(2)一个平行四边形和一个三角形等底等高。已知三角形的面积是68 dm2,则平行四边形的面积是( )dm2。
(3)一张长是10 cm、宽是7 cm的长方形纸,最多能剪( )个直径是2 cm的圆片。
(4)估计下图的面积约为( )cm2。(每格的面积是1 cm2)
第2课时 平面图形的周长与面积
15
答案不唯一
50
2.在方格纸上分别画一个三角形和一个梯形,使它们都与图中平行四边形的面积相等。
第2课时 平面图形的周长与面积
答案不唯一
3.计算下面各图形的周长和面积。(单位:cm)
第2课时 平面图形的周长与面积
8+6+10=24(cm)
8×6÷2=24(cm2)
3.计算下面各图形的周长和面积。(单位:cm)
第2课时 平面图形的周长与面积
3.14×20÷2+18×2+20=87.4(cm),
20×16+3.14×(20÷2)2÷2=477(cm2)
4.如下图,明明的妈妈在自己家的院墙边用篱笆围了一个牛栏,篱笆全长20.5 m,牛栏的占地面积是多少平方米?
(20.5-8.5)×8.5÷2=51(m2)
第2课时 平面图形的周长与面积
5.小明沿着一个圆形水池的外沿走了一周,正好走了50步,每步的距离约是0.628 m。这个水池的占地面积约是多少平方米?
0.628×50=31.4(m)
3.14×(31.4÷3.14÷2)2=78.5(m2)
第2课时 平面图形的周长与面积
6.如下图所示,梯形的上底是18 cm,下底是34 cm,阴影部分的面积是510 cm2。这个梯形的面积是多少平方厘米?
510×2÷34=30(cm)
(18+34)×30÷2=780(cm2)
第2课时 平面图形的周长与面积
7.胡伯伯在超市买了4瓶啤酒,售货员将4瓶啤酒捆扎在一起,捆扎方法如下图所示。照这样捆3圈至少用绳子多少厘米?(接头处不计)
(3.14×6+4×6)×3=128.52(cm)
第2课时 平面图形的周长与面积
8.如下图所示,正方形的面积是60 cm2,空白部分的面积是多少平方厘米?
锦囊妙计 圆的半径的平方等于正方形的面积。
第2课时 平面图形的周长与面积
1.填空题。
(1)小明用正方体木块摆成一个立体图形,从三个不同方位看到的形状如下图。摆这个立体图形至少用( )个小正方体,最多用( )个小正方体。
第3课时 立体图形
13
15
(2)一个圆柱的底面周长是25.12 cm,高是8 cm,它的侧面积是( )cm2,它的体积是( )cm3。
(3)一个长方体的底面积是0.4 m2,高是6 dm,它的体积是( )dm3。
(4)一个圆柱形容器中盛满14.13 L水,用这些水倒满一个与它等底等高的圆锥形容器,圆柱形容器中还剩( )L水。
第3课时 立体图形
200.96
401.92
240
9.42
第3课时 立体图形
2.判断题。(对的画“√”,错的画“×”)
(1)表面积相等的两个长方体,它们的体积一定相等。 ( )
(2)用同一张长方形硬纸,可以卷成两个不同的圆柱,它们的体积相等。 ( )
(3)把一个圆柱削成一个最大的圆锥,这个
圆锥的体积是这个圆柱体积的 ( )
×
×
√
3.求下面图形的体积。(单位:dm)
第3课时 立体图形
3.求下面图形的体积。(单位:dm)
第3课时 立体图形
3.14×[(6÷2)2-(4÷2)2]×8=125.6(dm3)
4.一个长方体正好可以切成5个同样大小的正方体,切成的5个正方体的表面积之和比原来长方体的表面积增加了200 cm2。原来长方体的表面积是多少平方厘米?
200÷8=25(cm2)
(5×4+2)×25=550(cm2)
第3课时 立体图形
5.一个棱长是4 dm的正方体容器装满水后,将这些水倒入一个底面积是12 dm2的圆锥形容器里正好装满,这个圆锥形容器的高是多少分米?(容器厚度不计)
第3课时 立体图形
6.一辆货车车厢是一个长方体,它的长是4 m,宽是1.5 m,高是4 dm。如果装满一车沙子,卸后将沙子堆成一个高是5 dm的圆锥,那么这个圆锥的底面积是多少平方米?
第3课时 立体图形
1.填空题。
(1)在括号里填上合适的数或单位。
0.15时=( )分
3500平方米=( )公顷
一瓶果汁的体积大约是300( )。
一个苹果的质量大约是200( )。
第4课时 练习十八
9
0.35
mL
g
第4课时 练习十八
(2)观察 下面这些图分别
是从哪个方向看到的?
左面
上面
前面
2.求阴影部分的面积。
第4课时 练习十八
2.求阴影部分的面积。
第4课时 练习十八
3.如下图所示,一个箱子的下半部分是长方体,这个长方体的长是40 cm,宽是30 cm,高是20 cm,上半部分是圆柱的一半。求这个箱子的表面积和体积。
第4课时 练习十八
第4课时 练习十八
第4课时 练习十八
4.右图所示的立体图形是由棱长为2 cm的小正方体搭成的,所有的表面都涂色。其中,只有1个面涂色的小正方体有( )个;只有2个面涂色的小正方体有( )个;只有3个面涂色的小正方体有( )个;只有4个面涂色的小正方体有( )个;只有5个面涂色的小正方体有( )个。该立体图形的表面积是( )cm2。
锦囊妙计 与其他的小正方体有n个面重合的小正方体,需要涂色的只有(6-n)个面。
第4课时 练习十八
第4课时 练习十八
4.右图所示的立体图形是由棱长为2 cm的小正方体搭成的,所有的表面都涂色。其中,只有1个面涂色的小正方体有( )个;只有2个面涂色的小正方体有( )个;只有3个面涂色的小正方体有( )个;只有4个面涂色的小正方体有( )个;只有5个面涂色的小正方体有( )个。该立体图形的表面积是( )cm2。
1
0
1
4
2
120
5.施工队用混凝土浇筑成一个无盖的长方体水槽(如下图),从外面量长是10 dm,宽是6 dm,高是5 dm。混凝土厚1 dm。
(1)请计算这个水槽的容积。
(10-1×2)×(6-1×2)×(5-1)=128(dm3)
第4课时 练习十八
(2)若给水槽的里面、外面均贴上瓷砖(水槽的外底面不贴),则贴瓷砖的面积是多少?
(10×5+6×5)×2+(10-1×2)×(5-1)×2+(6-1×2)×(5-1)×2+(10-1×2)×(6-1×2)=288(dm2)
288+10×6-(10-1×2)×(6-1×2)=316(dm2)
第4课时 练习十八
1.选择题。(把正确答案的序号填在括号里
(1)下列图形中,对称轴最多的是( )。
第5课时 图形的运动
B
(2) 观察下图,图①( )得到图②。
(A)先绕点O顺时针旋转90°,再向右平移10格
(B)先绕点O逆时针旋转90°,再向右平移10格
(C)先绕点O顺时针旋转90°,再向右平移8格
第5课时 图形的运动
B
第5课时 图形的运动
2.按要求画出图形。
(1)按对称轴将图①补完整。
(2)将(1)中补完整的图①向右平移9格,得到图②。
(3)把图②左下角的顶点记为点O,将图②绕点O逆时针旋转90°,得到图③。
(4)将图③按1∶2缩小,得到图④。
(图④位置不唯一 )
3.一个长是12 cm、宽是9 cm的长方形按1∶3缩小后,缩小的长方形的面积与原长方形的面积的比是( ),缩小的长方形的周长是原长方形周长
的
第5课时 图形的运动
1∶9
1
3
锦囊妙计 把一个长方形按1∶3缩小就是把这
个长方形的长和宽缩小到原来的
1.下面哪些图形是轴对称图形?画出它们所有的对称轴。
第6课时 练习十九
第1、2、4个图形是轴对称图形。
2.下面5个图形的阴影部分面积相等吗?为什么?
它们阴影部分的面积( )。因为图②③④⑤中的各部分图案经过平移和( )后都能变成图( )。
第6课时 练习十九
相等
旋转
①
3.(1)将图①向右平移3格后得到图②;以直线a为对称轴,作图②的轴对称图形,得到图③。
(2)画出三角形绕点O逆时针旋转90°后的图形。
(3)画出长方形按2∶1放大后的图形。
第6课时 练习十九
4.你能利用平移和旋转的方法,将图2恢复到图1的样子吗?请你把“恢复”的过程写下来。
第6课时 练习十九
锦囊妙计 根据平移和旋转的特点结合图1和图2来比较分析。
图2中的左下角图形先向上平移2格,再向右平移2格。右下角的图形先向左平移2格,再绕该图形的左上角顶点逆时针旋转90°。
第6课时 练习十九
1.以学校为观测点。
(1)公园在学校的( )偏( )( )°方向( )m处。
(2)体育场在学校的( )方向( )m处。
(3)农贸市场在学校的( )偏( )( )°方向( )m处。
第7课时 图形与位置
北
东
50
500
正北
200
南
西
35
400
2.在游乐场示意图已标出的位置上写出各个项目的名称,并填空。
第7课时 图形与位置
5,4
(1)大门位于点(0,1),向东走200 m到达旋转木马。
(2)碰碰车位于点( ),在旋转木马的北偏( )( )°方向上。
东
45
(3)云霄飞车位于点(3,6),在碰碰车的( )偏( )( )°方向上。
(4)摩天轮到旋转木马和云霄飞车的距离相等,它位于点( )。
第7课时 图形与位置
北
西
45
5,3
(5)山洞飞车位于点(7,7),向西走600 m到达激流勇进;秋千与这两处距离相等,它位于点( )。
第7课时 图形与位置
4,8
3.量一量,画一画。
(1)轮船在灯塔的北偏( )( )°方向( )m处。
第7课时 图形与位置
西
60
400
第8课时 练习二十
1.彤彤一家到公园玩。
(1)公园大门的位置是( ),动物园的位置是( ),荷花池的位置是( )。( )的位置是(8,5)。
4,6
8,8
12,6
餐厅
第8课时 练习二十
(2)游乐场的位置是(5,2),请在图中标出来。
方向 路程/米 时间/分钟
王老师家→博物馆 8
博物馆→小伟家 11
小伟家→博物馆 9
博物馆→王老师家 7
2.周末,王老师去小伟家家访。
第8课时 练习二十
北偏东65°
450
南偏东55°
600
北偏西55°
600
南偏西65°
450
(1)根据路线图,说一说王老师去小伟家家访和回来时所走的方向和路程,并完成下表。
(2)王老师走完全程的平均速度是多少?
锦囊妙计 用总路程除以总时间。
第8课时 练习二十
60米/分
