18.4 反比例[函数[下学期]
图片预览




文档简介
课件12张PPT。要点、考点聚焦1、反比例函数的定义:一般地,函数y=k/x(k是常数,
k≠0),叫做反比例函数. 2、反比例函数y=k/x(k是常数,k≠0)的图像是双曲线 3、反比例函数的性质.
(1)当k>0时,图像的两个分支分别在第一、三象限内,
在每个象限内,y随x的增大而减小.
(2)当k<0时,图像的两个分支分别在第二、四象限内,
在每个象限内,y随x的增大而增大.
1.(2004年·河北省)若反比例函数y=k/x的图像过点
(3,-4),则此函数的解析式为:
。课前热身2.(2004年·重庆市)已知反比例函数y=k/x与一次函数
y=2x+k的图像的一个交点的纵坐标是-4,则k的值
是 。-83.(2004年·山西省)下列命题中,不正确的是( )
A.
B.函数y=2x-1的图像与x轴只有一个交点
C.一次函数y=-2x-1的图像经过第二、三、四象限
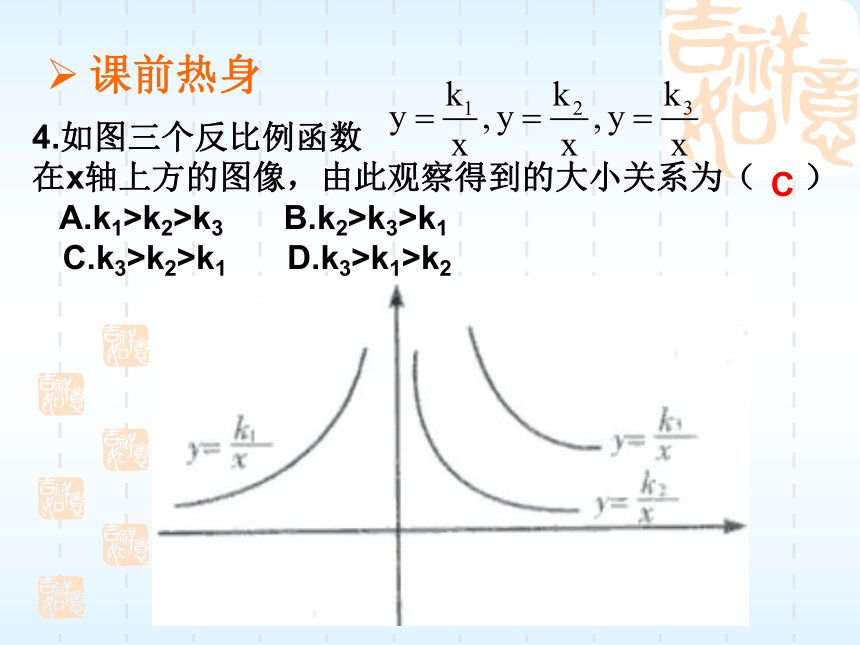
D.在函数y=-1/2x中,y随x的增大而增大D4.如图三个反比例函数
在x轴上方的图像,由此观察得到的大小关系为( )
A.k1>k2>k3 B.k2>k3>k1
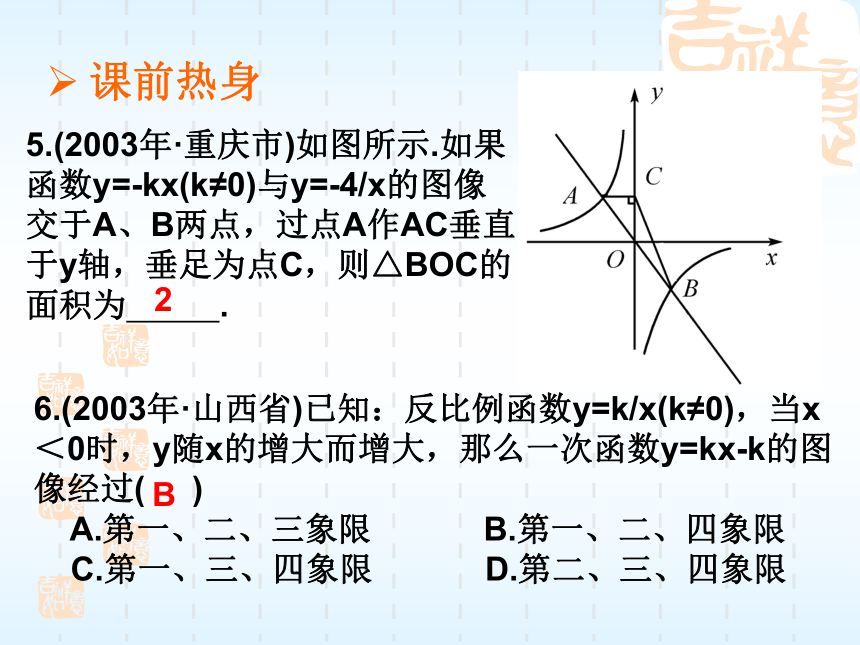
C.k3>k2>k1 D.k3>k1>k2C课前热身5.(2003年·重庆市)如图所示.如果
函数y=-kx(k≠0)与y=-4/x的图像
交于A、B两点,过点A作AC垂直
于y轴,垂足为点C,则△BOC的
面积为 . 2课前热身6.(2003年·山西省)已知:反比例函数y=k/x(k≠0),当x
<0时,y随x的增大而增大,那么一次函数y=kx-k的图
像经过( )
A.第一、二、三象限 B.第一、二、四象限
C.第一、三、四象限 D.第二、三、四象限 B【例1】 (2003年·广西)已知反比例函数y=-1/x的图像上有两点A(x1,y1),B(x2,y2),且x1<x2,那么下列结论正确的是 ( )
A.y1<y2 B.y1>y2
C.y1=y2 D.y1与y2之间的大小关系不能确定典型例题解析D【例2】 (2003年·陕西省)已知反比例函数y=k/x的图像经过点A(-2,3),
(1)求出这个反比例函数的解析式.
(2)经过点A的正比例函数y=k′x的图像与反比例函数y=k/x的图像还有其他交点吗?若有,求出交点坐标;若没有,说明理由.
1、反比例函数的解析式为:y=- 6/x2、有.
∵正、反比例函数的图像均关于原点对称,且点
A在它们的图像上,
∴A(-2,3)关于原点的对称点B(2,-3)也在它们的
图像上.
∴它们相交的另一交点坐标为(2,-3).
【例3】 (2003年·天津市)如图3-3-3所示,已知一次函数y=kx+b(k≠0)的图像与x轴、y轴分别交于A、B两点,且与反比例函数y=m/x(m≠0)的图像在第一象限交于C点,CD垂直于x轴,垂足为D.若OA=OB=OD=1.
(1)求点A、B、D的坐标;
(2)求一次函数和反比例函数的解析式.
1、点A、B、D的坐标分别为
A(-1,0)、B(0,1)、D(1,0) 2、反比例函数的解析式为:y=2/x. 典型例题解析1.研究反比例函数及其图像时:
(1)易漏隐含条件;
(2)研究函数增减性时不分象限,笼统地说:“当k>0
时,y随x的增大而减小;当k<0时,y随x的增大而增
大.”这种说法是错误的,应将两个分支分别讨论.
2.过双曲线上任一点作x轴、y轴的垂线,所得矩形的
面积等于|k|. 方法小结:课时训练1.(2002年·泸州市)如图所示,当k<0时,反比例函数
y=k/x和一次函数y=kx+2的图像大致是图 ( )
B2.(2002年·武汉市)若点(3,4)是反比例函数
的图像上一点,则此函数图像必经过点( )
A.(2,6) B.(2,-6) C.(4,-3) D.(3,-4)A3.如图所示,正比例函数y=kx (k>0)
与反比例函数y=1/x的图像相交于A、C
两点,过A作x轴的垂线交x轴于B,
连接BC.若△ABC面积为S,则
( )
A.S=1 B.S=2
C.S=3 D.不能确定A课时训练4.已知:y=y1+y2,其中y1与x成反比,且比例系数是k1
,y2与x2成正比,且比例系数是k2,若x=-1时,y=0,
则k1与k2的关系是( )
A.k1+k2=0 B.k1-k2=0
C.k1·k2=1 D.k1·k2=-1
B5.如图所示,已知点P是反
比例函数y=k/x的图像在第
二象限内的一点,过P点分
别作x轴、y轴的垂线,垂
足为M、N,若矩形OMPN
的面积为5,则k= . -5课时训练6.已知反比例函数y=(1-2m)/x的图像上有两点
A(x1,y1),B(x2,y2),当x1<0<x2时,有y1<y2.
则m的取值范围是 ( )
A.m<0 B.m>0
C.m> 1/2 D.m<1/2 D课时训练
k≠0),叫做反比例函数. 2、反比例函数y=k/x(k是常数,k≠0)的图像是双曲线 3、反比例函数的性质.
(1)当k>0时,图像的两个分支分别在第一、三象限内,
在每个象限内,y随x的增大而减小.
(2)当k<0时,图像的两个分支分别在第二、四象限内,
在每个象限内,y随x的增大而增大.
1.(2004年·河北省)若反比例函数y=k/x的图像过点
(3,-4),则此函数的解析式为:
。课前热身2.(2004年·重庆市)已知反比例函数y=k/x与一次函数
y=2x+k的图像的一个交点的纵坐标是-4,则k的值
是 。-83.(2004年·山西省)下列命题中,不正确的是( )
A.
B.函数y=2x-1的图像与x轴只有一个交点
C.一次函数y=-2x-1的图像经过第二、三、四象限
D.在函数y=-1/2x中,y随x的增大而增大D4.如图三个反比例函数
在x轴上方的图像,由此观察得到的大小关系为( )
A.k1>k2>k3 B.k2>k3>k1
C.k3>k2>k1 D.k3>k1>k2C课前热身5.(2003年·重庆市)如图所示.如果
函数y=-kx(k≠0)与y=-4/x的图像
交于A、B两点,过点A作AC垂直
于y轴,垂足为点C,则△BOC的
面积为 . 2课前热身6.(2003年·山西省)已知:反比例函数y=k/x(k≠0),当x
<0时,y随x的增大而增大,那么一次函数y=kx-k的图
像经过( )
A.第一、二、三象限 B.第一、二、四象限
C.第一、三、四象限 D.第二、三、四象限 B【例1】 (2003年·广西)已知反比例函数y=-1/x的图像上有两点A(x1,y1),B(x2,y2),且x1<x2,那么下列结论正确的是 ( )
A.y1<y2 B.y1>y2
C.y1=y2 D.y1与y2之间的大小关系不能确定典型例题解析D【例2】 (2003年·陕西省)已知反比例函数y=k/x的图像经过点A(-2,3),
(1)求出这个反比例函数的解析式.
(2)经过点A的正比例函数y=k′x的图像与反比例函数y=k/x的图像还有其他交点吗?若有,求出交点坐标;若没有,说明理由.
1、反比例函数的解析式为:y=- 6/x2、有.
∵正、反比例函数的图像均关于原点对称,且点
A在它们的图像上,
∴A(-2,3)关于原点的对称点B(2,-3)也在它们的
图像上.
∴它们相交的另一交点坐标为(2,-3).
【例3】 (2003年·天津市)如图3-3-3所示,已知一次函数y=kx+b(k≠0)的图像与x轴、y轴分别交于A、B两点,且与反比例函数y=m/x(m≠0)的图像在第一象限交于C点,CD垂直于x轴,垂足为D.若OA=OB=OD=1.
(1)求点A、B、D的坐标;
(2)求一次函数和反比例函数的解析式.
1、点A、B、D的坐标分别为
A(-1,0)、B(0,1)、D(1,0) 2、反比例函数的解析式为:y=2/x. 典型例题解析1.研究反比例函数及其图像时:
(1)易漏隐含条件;
(2)研究函数增减性时不分象限,笼统地说:“当k>0
时,y随x的增大而减小;当k<0时,y随x的增大而增
大.”这种说法是错误的,应将两个分支分别讨论.
2.过双曲线上任一点作x轴、y轴的垂线,所得矩形的
面积等于|k|. 方法小结:课时训练1.(2002年·泸州市)如图所示,当k<0时,反比例函数
y=k/x和一次函数y=kx+2的图像大致是图 ( )
B2.(2002年·武汉市)若点(3,4)是反比例函数
的图像上一点,则此函数图像必经过点( )
A.(2,6) B.(2,-6) C.(4,-3) D.(3,-4)A3.如图所示,正比例函数y=kx (k>0)
与反比例函数y=1/x的图像相交于A、C
两点,过A作x轴的垂线交x轴于B,
连接BC.若△ABC面积为S,则
( )
A.S=1 B.S=2
C.S=3 D.不能确定A课时训练4.已知:y=y1+y2,其中y1与x成反比,且比例系数是k1
,y2与x2成正比,且比例系数是k2,若x=-1时,y=0,
则k1与k2的关系是( )
A.k1+k2=0 B.k1-k2=0
C.k1·k2=1 D.k1·k2=-1
B5.如图所示,已知点P是反
比例函数y=k/x的图像在第
二象限内的一点,过P点分
别作x轴、y轴的垂线,垂
足为M、N,若矩形OMPN
的面积为5,则k= . -5课时训练6.已知反比例函数y=(1-2m)/x的图像上有两点
A(x1,y1),B(x2,y2),当x1<0<x2时,有y1<y2.
则m的取值范围是 ( )
A.m<0 B.m>0
C.m> 1/2 D.m<1/2 D课时训练
