相似三角形[下学期]
图片预览




文档简介
课件20张PPT。相似图形 一、相似三角形
1.相似三角形性质:
①相似三角形的对应角相等,对应边成比例.
②相似三角形对应中线的比,对应角平分线的 比,对应高的比,对应周长的比都等于相似比.
③相似三角形面积的比等于相似比的平方.1.定理 两角对应相等的两个三角形相似.(AA)2.推论1 平行于三角形一边直线截其它两边(或其延长线),所截得的三角形与原三角形相似;
如图:如果DE∥BC,那么△ADE∽△ABC3、三角形相似的判定方法2.推论1 平行于三角形一边直线截其它两边(或其延长线),所截得的三角形与原三角形相似;
如图:如果DE∥BC,那么△ADE∽△ABC3.推论2 平行于三角形一边直线截其它两边(或其延长线),所得的对应线段成比例.
如果DE∥BC,4.相似三角形与全等三角形的关系:
相似比等于1的两个三角形全等.若DE‖BC,则△ADE∽△ABC
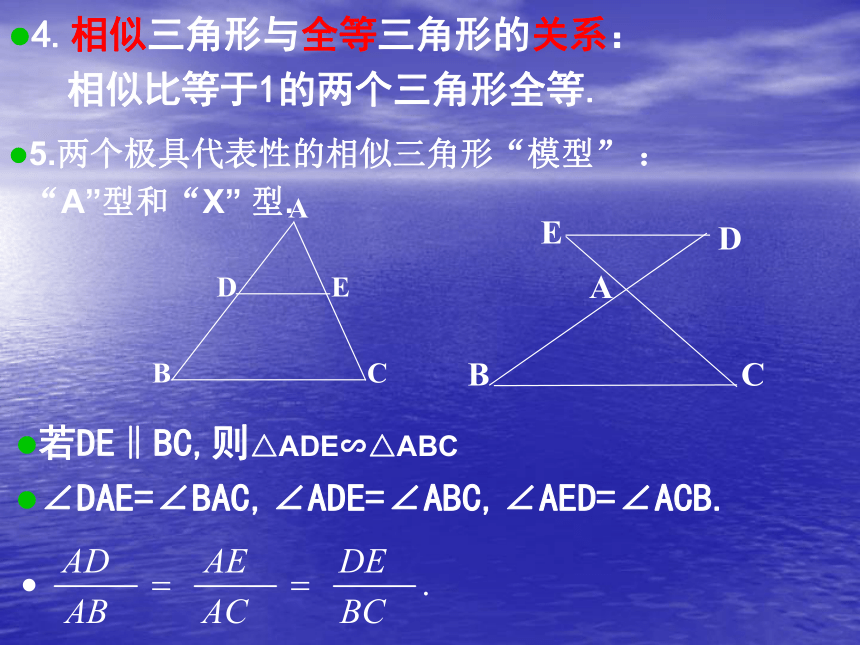
∠DAE=∠BAC,∠ADE=∠ABC,∠AED=∠ACB.5.两个极具代表性的相似三角形“模型” :
“A”型和“X” 型.6.定理 三边对应成比例的两个三角形相似.
(SSS)
7.定理 两边对应成比例,且夹角相等的两个三角形相似;(SAS)
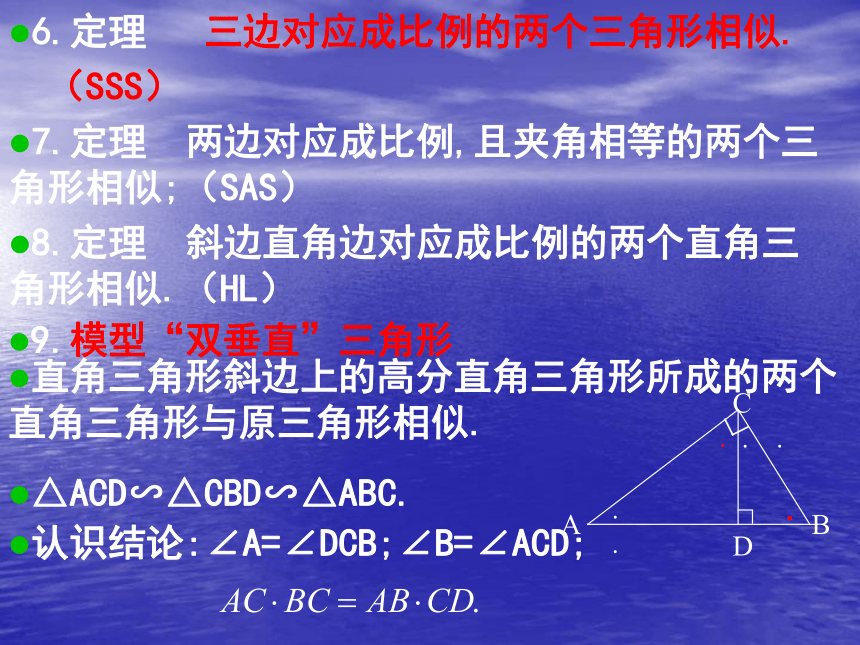
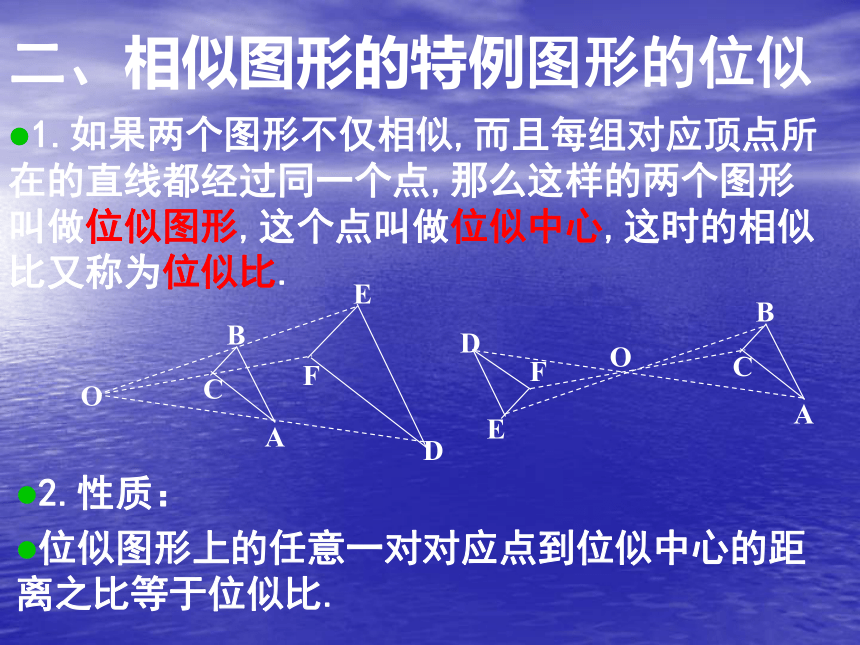
8.定理 斜边直角边对应成比例的两个直角三角形相似.(HL)9.模型“双垂直”三角形△ACD∽△CBD∽△ABC.认识结论:∠A=∠DCB;∠B=∠ACD; 直角三角形斜边上的高分直角三角形所成的两个直角三角形与原三角形相似.二、相似图形的特例图形的位似1.如果两个图形不仅相似,而且每组对应顶点所在的直线都经过同一个点,那么这样的两个图形叫做位似图形,这个点叫做位似中心,这时的相似比又称为位似比.2.性质:
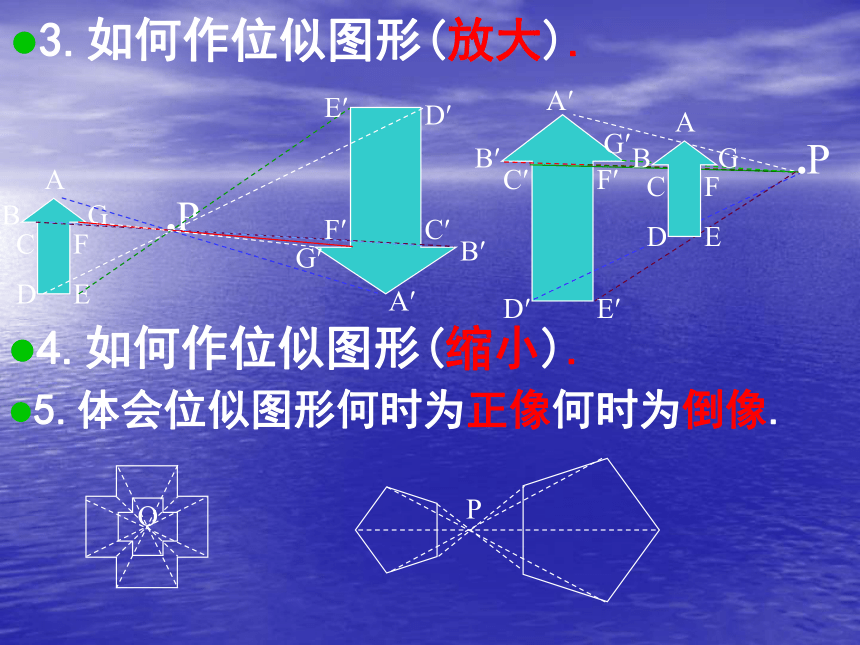
位似图形上的任意一对对应点到位似中心的距离之比等于位似比.3.如何作位似图形(放大).5.体会位似图形何时为正像何时为倒像.4.如何作位似图形(缩小).6.黄金分割如图,点C把线段AB分成两条线段AC和BC,
如果 那么称线段AB被点C
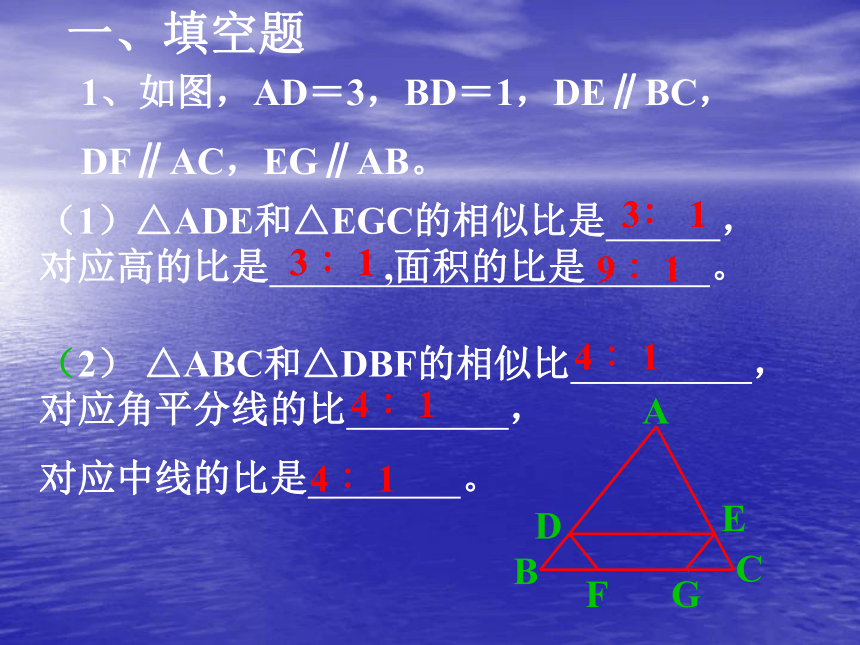
黄金分割,点C叫做线段AB的黄金分割点, 称 或 为黄金比.一、填空题1、如图,AD=3,BD=1,DE∥BC,
DF∥AC,EG∥AB。(1)△ADE和△EGC的相似比是 ,对应高的比是 ,面积的比是 。(2) △ABC和△DBF的相似比 ,对应角平分线的比 ,
对应中线的比是 。3∶ 14 ∶14 ∶14 ∶13 ∶19 ∶1判定下列三角形是否相似,若不相似需要增加什么条件才能相似?
两个全等三角形;
两个等腰三角形;
两个等边三角形;
两个直角三角形;
含300角的直角三角形;√√√一对应角相等一锐角相等提升能力的奥秘如图,P是AB上一点,补充下列条件:
(1) ∠ACP=∠B;
(2)∠APC=∠ACB;其中一定能使
△ ACP∽ △ABC的是( )
(A) (1) (2) (3) (4) (B) (1) (2) (3)
(C) (3) (D) (1) (2) (4)D活动与探究如图:直角三角形的铁片ABC的两条直角边BC,AC的长分别是3和4,用这些铁片剪出一块正方形铁片,求剪下最大的正方形铁片面积。已知,AB∥CD∥EF,
(1)图中有几对相似的三角形?
(2)线段AB、CD与EF有怎样的等量关系?比一比2.如图所示,在△ABC中,底边BC=60cm,高 AD=40cm,四边形PQRS是正方形.
(1)△ASR与△ABC相似吗?为什么?
(2)求正方形PQRS的边长.解:设正方形边长为x
∵△ASR与△ABC相似
3.下列说法正确的是( )
A 所有的等腰三角形都相似
B所有的直角三角形都相似
C所有的等腰直角三角形都相似
D有一个角相等的两个等腰三角形都相似
4.在长度为1的线段上找到两个黄金分割点P、Q。则PQ=( )
A B
C D 5.在直角坐标系中,点A(-2,0),B(0,4),C(0,3)。过点C作直线交x轴于点D,使以D、O、C为顶点的三角形与ΔAOB相似,这样的直线最多可以作( )条
A 2 B 3 C 4 D 6
ABCDDODD
6.如果整张报纸与半张报纸相似,则整张报纸长与宽的比是( )
A B 4:1 C 2:1 D YXX7.如图,∠APD=900,AP=PB=BC=CD,则下列结论成立的是( )
A ΔPAB∽ΔPCA B ΔPAB∽ΔPDA
C ΔABC ∽ ΔDBA
D ΔABC∽ΔDCAC8.如图在梯形ABCD中,AD∥BC,∠A=90°,BD⊥DC,试问:
(1)△ABD与△DCB相似吗?
请说明理由.
(2)如果AD=3, BC=5, 你能求出BD的长吗?9.在AB=20米,AD=30米的矩形ABCD的花坛四周修筑小路:
(1)如果四周的小路的宽均相等,那么小路四所围成的矩形和矩形ABCD相似吗?请说明理由
(2)如果相对两条小路的宽均相等,试问小路的宽x与y的比值为多少时,能使小路四周所围成矩形和矩形ABCD相似?请说明理由.
1.相似三角形性质:
①相似三角形的对应角相等,对应边成比例.
②相似三角形对应中线的比,对应角平分线的 比,对应高的比,对应周长的比都等于相似比.
③相似三角形面积的比等于相似比的平方.1.定理 两角对应相等的两个三角形相似.(AA)2.推论1 平行于三角形一边直线截其它两边(或其延长线),所截得的三角形与原三角形相似;
如图:如果DE∥BC,那么△ADE∽△ABC3、三角形相似的判定方法2.推论1 平行于三角形一边直线截其它两边(或其延长线),所截得的三角形与原三角形相似;
如图:如果DE∥BC,那么△ADE∽△ABC3.推论2 平行于三角形一边直线截其它两边(或其延长线),所得的对应线段成比例.
如果DE∥BC,4.相似三角形与全等三角形的关系:
相似比等于1的两个三角形全等.若DE‖BC,则△ADE∽△ABC
∠DAE=∠BAC,∠ADE=∠ABC,∠AED=∠ACB.5.两个极具代表性的相似三角形“模型” :
“A”型和“X” 型.6.定理 三边对应成比例的两个三角形相似.
(SSS)
7.定理 两边对应成比例,且夹角相等的两个三角形相似;(SAS)
8.定理 斜边直角边对应成比例的两个直角三角形相似.(HL)9.模型“双垂直”三角形△ACD∽△CBD∽△ABC.认识结论:∠A=∠DCB;∠B=∠ACD; 直角三角形斜边上的高分直角三角形所成的两个直角三角形与原三角形相似.二、相似图形的特例图形的位似1.如果两个图形不仅相似,而且每组对应顶点所在的直线都经过同一个点,那么这样的两个图形叫做位似图形,这个点叫做位似中心,这时的相似比又称为位似比.2.性质:
位似图形上的任意一对对应点到位似中心的距离之比等于位似比.3.如何作位似图形(放大).5.体会位似图形何时为正像何时为倒像.4.如何作位似图形(缩小).6.黄金分割如图,点C把线段AB分成两条线段AC和BC,
如果 那么称线段AB被点C
黄金分割,点C叫做线段AB的黄金分割点, 称 或 为黄金比.一、填空题1、如图,AD=3,BD=1,DE∥BC,
DF∥AC,EG∥AB。(1)△ADE和△EGC的相似比是 ,对应高的比是 ,面积的比是 。(2) △ABC和△DBF的相似比 ,对应角平分线的比 ,
对应中线的比是 。3∶ 14 ∶14 ∶14 ∶13 ∶19 ∶1判定下列三角形是否相似,若不相似需要增加什么条件才能相似?
两个全等三角形;
两个等腰三角形;
两个等边三角形;
两个直角三角形;
含300角的直角三角形;√√√一对应角相等一锐角相等提升能力的奥秘如图,P是AB上一点,补充下列条件:
(1) ∠ACP=∠B;
(2)∠APC=∠ACB;其中一定能使
△ ACP∽ △ABC的是( )
(A) (1) (2) (3) (4) (B) (1) (2) (3)
(C) (3) (D) (1) (2) (4)D活动与探究如图:直角三角形的铁片ABC的两条直角边BC,AC的长分别是3和4,用这些铁片剪出一块正方形铁片,求剪下最大的正方形铁片面积。已知,AB∥CD∥EF,
(1)图中有几对相似的三角形?
(2)线段AB、CD与EF有怎样的等量关系?比一比2.如图所示,在△ABC中,底边BC=60cm,高 AD=40cm,四边形PQRS是正方形.
(1)△ASR与△ABC相似吗?为什么?
(2)求正方形PQRS的边长.解:设正方形边长为x
∵△ASR与△ABC相似
3.下列说法正确的是( )
A 所有的等腰三角形都相似
B所有的直角三角形都相似
C所有的等腰直角三角形都相似
D有一个角相等的两个等腰三角形都相似
4.在长度为1的线段上找到两个黄金分割点P、Q。则PQ=( )
A B
C D 5.在直角坐标系中,点A(-2,0),B(0,4),C(0,3)。过点C作直线交x轴于点D,使以D、O、C为顶点的三角形与ΔAOB相似,这样的直线最多可以作( )条
A 2 B 3 C 4 D 6
ABCDDODD
6.如果整张报纸与半张报纸相似,则整张报纸长与宽的比是( )
A B 4:1 C 2:1 D YXX7.如图,∠APD=900,AP=PB=BC=CD,则下列结论成立的是( )
A ΔPAB∽ΔPCA B ΔPAB∽ΔPDA
C ΔABC ∽ ΔDBA
D ΔABC∽ΔDCAC8.如图在梯形ABCD中,AD∥BC,∠A=90°,BD⊥DC,试问:
(1)△ABD与△DCB相似吗?
请说明理由.
(2)如果AD=3, BC=5, 你能求出BD的长吗?9.在AB=20米,AD=30米的矩形ABCD的花坛四周修筑小路:
(1)如果四周的小路的宽均相等,那么小路四所围成的矩形和矩形ABCD相似吗?请说明理由
(2)如果相对两条小路的宽均相等,试问小路的宽x与y的比值为多少时,能使小路四周所围成矩形和矩形ABCD相似?请说明理由.
