人教版 六年级下册数学 3 圆柱与圆锥 单元课件(共84张PPT)
文档属性
| 名称 | 人教版 六年级下册数学 3 圆柱与圆锥 单元课件(共84张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-13 12:28:51 | ||
图片预览




文档简介
(共84张PPT)
3 圆柱与圆锥
数学配人教版
(六年级/下册)
第1课时 圆柱的认识和练习三
第2课时 圆柱的表面积
第3单元巩固练习
第3课时 练习四
第4课时 圆柱的体积(1)
第5课时 圆柱的体积(2)
第6课时 练习五
第7课时 圆锥的认识
第8课时 圆锥的体积
第9课时 练习六
第10课时 练习七
快乐导航
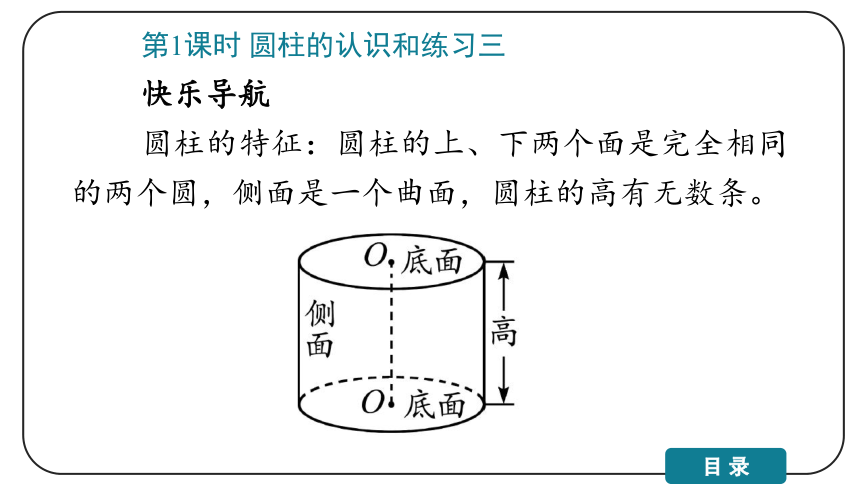
圆柱的特征:圆柱的上、下两个面是完全相同的两个圆,侧面是一个曲面,圆柱的高有无数条。
第1课时 圆柱的认识和练习三
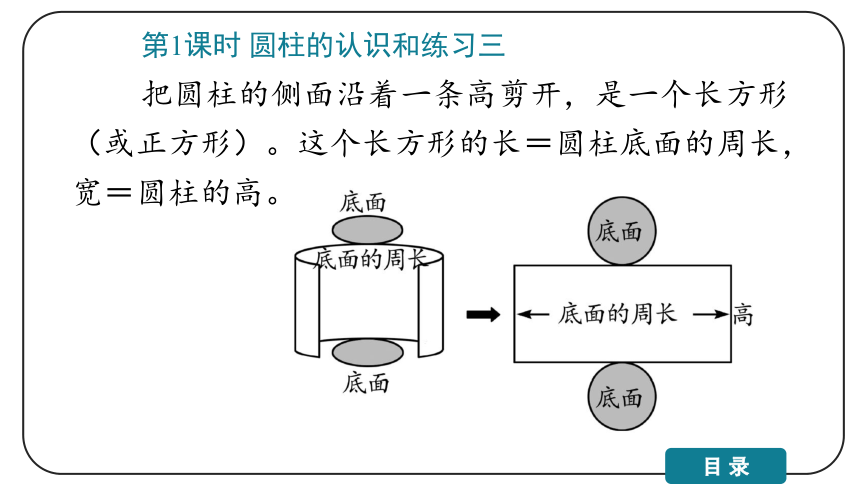
把圆柱的侧面沿着一条高剪开,是一个长方形(或正方形)。这个长方形的长=圆柱底面的周长,宽=圆柱的高。
第1课时 圆柱的认识和练习三
小试身手
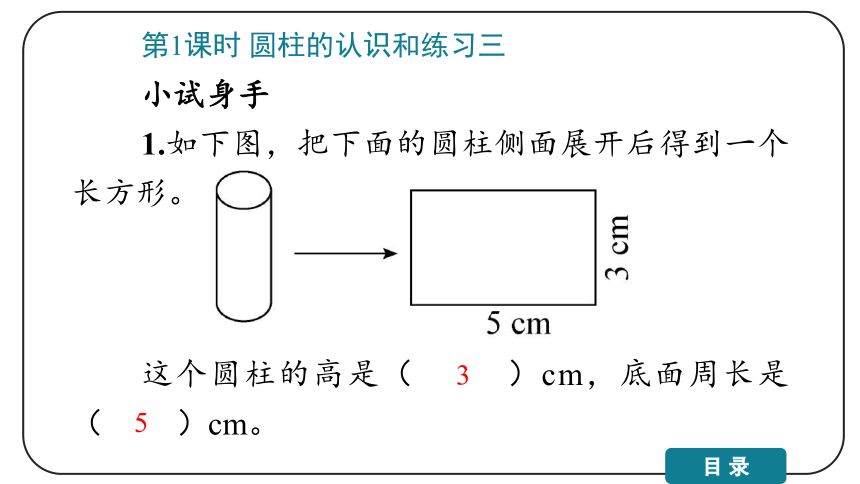
1.如下图,把下面的圆柱侧面展开后得到一个长方形。
第1课时 圆柱的认识和练习三
这个圆柱的高是( )cm,底面周长是( )cm。
3
5
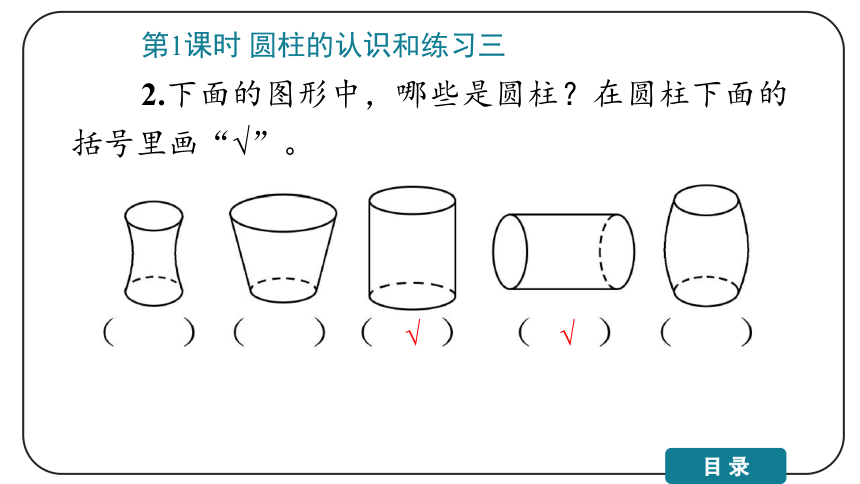
2.下面的图形中,哪些是圆柱?在圆柱下面的括号里画“√”。
第1课时 圆柱的认识和练习三
√
√
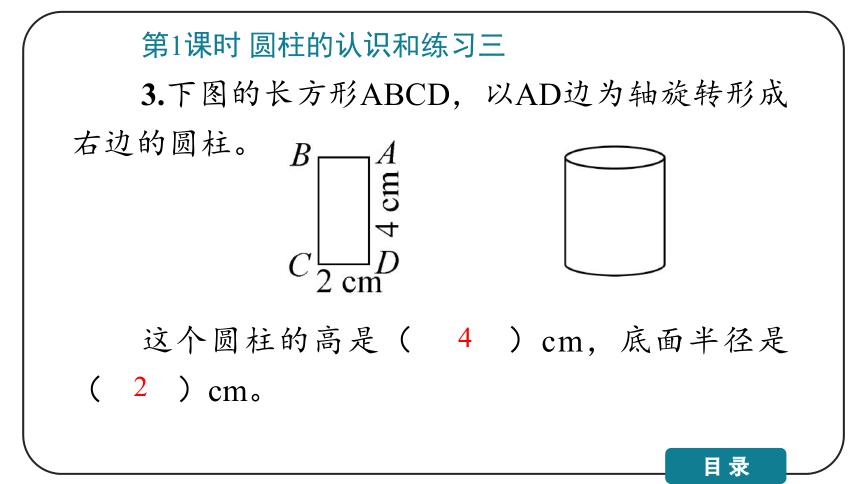
3.下图的长方形ABCD,以AD边为轴旋转形成右边的圆柱。
这个圆柱的高是( )cm,底面半径是( )cm。
4
2
第1课时 圆柱的认识和练习三
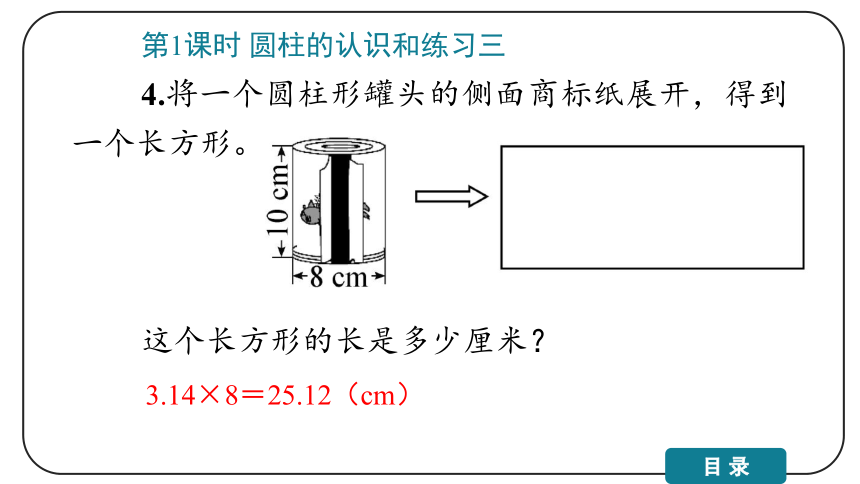
4.将一个圆柱形罐头的侧面商标纸展开,得到一个长方形。
这个长方形的长是多少厘米?
3.14×8=25.12(cm)
第1课时 圆柱的认识和练习三
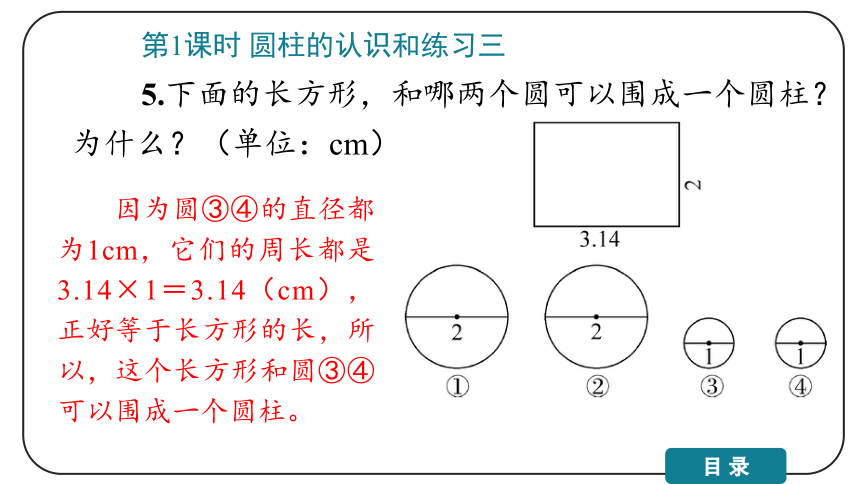
5.下面的长方形,和哪两个圆可以围成一个圆柱?为什么?(单位:cm)
因为圆③④的直径都为1cm,它们的周长都是3.14×1=3.14(cm),正好等于长方形的长,所以,这个长方形和圆③④可以围成一个圆柱。
第1课时 圆柱的认识和练习三
快乐导航
1.圆柱的侧面积=底面周长×高
2.圆柱的表面积=圆柱的侧面积+两个底面的面积
3.在解决圆柱表面积的实际应用问题时,有时只需要计算圆柱的一个底面,有时不需要计算圆柱的底面。解题时要根据实际情况进行计算。
第2课时 圆柱的表面积
小试身手
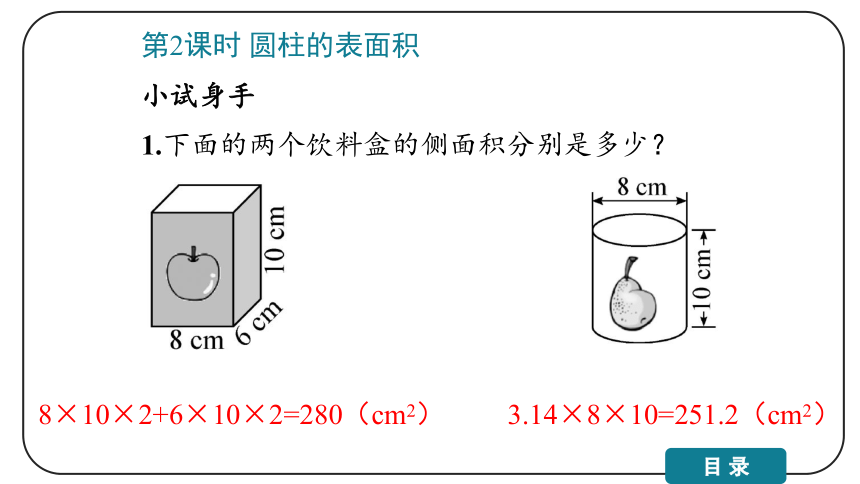
1.下面的两个饮料盒的侧面积分别是多少?
第2课时 圆柱的表面积
8×10×2+6×10×2=280(cm2)
3.14×8×10=251.2(cm2)
2.(1)一个圆柱的底面周长是3.14 cm,高是3 cm。它的侧面积是( )cm2。
(2)一个圆柱的底面直径是2 cm,高是3 cm。它的侧面积是( )cm2。
(3)一个圆柱的底面周长是3.14 cm,高是3 cm。它的一个底面的面积是( )cm2。
(4)一个圆柱的底面直径是2 cm,高是3 cm。它的一个底面的面积是( )cm2。
9.42
18.84
0.785
3.14
第2课时 圆柱的表面积
3.计算下面圆柱的表面积。
3.14×52=78.5(cm2)
2×3.14×5×12=376.8(cm2)
78.5×2+376.8=533.8(cm2)
第2课时 圆柱的表面积
4.做一个无盖的圆柱形铁皮水桶,底面直径为4 dm,高为 5 dm,至少需要多少平方分米的铁皮?
3.14×(4÷2)2=12.56(dm2)
3.14×4×5=62.8(dm2)
12.56+62.8=75.36(dm2)
第2课时 圆柱的表面积
1.求下面各圆柱的表面积。(单位:dm)
第3课时 练习四
3.14×(5÷2)2×2+3.14×5×20=353.25(dm2)
1.求下面各圆柱的表面积。(单位:dm)
第3课时 练习四
3.14×102×2+2×3.14×10×4=879.2(dm2)
2.以下是三个同学量出的某品牌茶叶罐的外包装数据,请你分别根据这三组数据计算出这个茶叶罐的表面积。
张丽:底面周长为25.12 cm,高为10 cm。
李亮:底面直径为8 cm,高为10 cm。
刘芳:底面半径为4 cm,高为10 cm。
第3课时 练习四
张丽:25.12÷3.14=8(cm),
3.14×(8÷2)2×2+3.14×8×10=351.68(cm2)
李亮:3.14×(8÷2)2×2+3.14×8×10=351.68(cm2)
刘芳:3.14×42×2+2×3.14×4×10=351.68(cm2)
3.把一根圆柱形木料如下图那样截成2段,得到2个小圆柱。那么这2个小圆柱的表面积之和与原圆柱形木料的表面积相比,( )。
(A)表面积增加
(B)表面积减少
(C)表面积不变
A
第3课时 练习四
4.一根圆柱形的通风管,直径是30 cm,长1 m。制作这样的一根通风管至少需要多少平方米的铁皮?
30cm=0.3m
3.14×0.3×1=0.942(m2)
第3课时 练习四
5.如右图,把一根圆柱形木料沿底面直径垂直切开,它的一半的表面积是多少平方厘米?
锦囊妙计 圆柱形木料的一半的表面积并不是原来圆柱形木料表面积的一半。
第3课时 练习四
上底和下底可以拼成一个圆,面积是
3.14×(20÷2)2=314(cm2)。
侧面由一个曲面和一个长方形组成,曲面的面积是3.14×20×30÷2=942(cm2),长方形的面积是20×30=600(cm2)。
整个图形的表面积是314+942+600=1856(cm2)。
第3课时 练习四
快乐导航
1.圆柱的体积计算公式推导如下:
圆柱的体积(容积)用含有字母的式子表示是V=Sh或V=πr2h。
第4课时 圆柱的体积(1)
2.在计算圆柱形容器的容积时,数据要从容器里面测量得到。
第4课时 圆柱的体积(1)
小试身手
1.下面长方体的体积是( )cm3,正方体的体积是( )cm3。
第4课时 圆柱的体积(1)
300
125
2.右边圆柱的体积是( )cm3。
75.36
第4课时 圆柱的体积(1)
3.计算下面各圆柱的体积。(单位:cm)
3.14×(4÷2)2×6=75.36(cm3)
第4课时 圆柱的体积(1)
3.计算下面各圆柱的体积。(单位:cm)
3.14×62×2=226.08(cm3)
第4课时 圆柱的体积(1)
4.一个圆柱形桶,从里面量,它的底面半径是1.5 dm,高是6 dm。这个圆柱形桶的容积是多少升?
3.14×1.52×6=42.39(dm3)
42.39dm3=42.39L
第4课时 圆柱的体积(1)
5.这根圆柱形木料最多能做多少个柜子?
3.14×0.32×5÷0.09=15.7(个)
最多能做15个柜子。
第4课时 圆柱的体积(1)
6.如下图所示,数据是从里面测量的。
3.14×(6÷2)2×10=282.6(cm3)
282.6cm3=282.6mL
282.6mL<300mL
这个罐子不能装下300mL的橙汁。
第4课时 圆柱的体积(1)
快乐导航
根据体积不变的特点,把不规则图形转化为圆柱求体积。
第5课时 圆柱的体积(2)
第5课时 圆柱的体积(2)
小试身手
1.下图所示的瓶子是不规则图形,请你分步算出它的容积。
(1)
3.14×(6÷2)2 ×10=282.6(cm3)
282.6cm3=282.6mL
(2)该瓶子上面无水部分的容积是多少毫升?
第5课时 圆柱的体积(2)
3.14×(6÷2)2×8=226.08(cm3 )
226.08 cm3 =226.08 mL
(3)该瓶子的容积是多少毫升?
第5课时 圆柱的体积(2)
282.6+226.08=508.68(mL)
2.一个装满水的圆柱形水杯,从里面量的数据如下图所示。
3.14×(10÷2)2×(10-6)=314(cm3)
314cm3=314mL
第5课时 圆柱的体积(2)
3.有一种饮料瓶的容积是600 mL。现在瓶中装有一些饮料,瓶子正放时饮料高度为20 cm,倒放时空余部分的高度为5 cm。瓶子中有饮料多少毫升?
600÷(20+5)×20=480(mL)
第5课时 圆柱的体积(2)
锦囊妙计 瓶子的容积600 mL相当于饮料的体积加上一个5 cm高的圆柱的体积,也就是(20+5)cm高的圆柱的体积。
1.一个圆柱形蓄水池,从外面量的底面半径是2.2 m,高是3 m。从里面量的底面半径是2 m,高是2.8 m。这个蓄水池的占地面积是( )m2,它所占的空间是( )m3,它最多能装水( )m3。
第6课时 练习五
15.1976
45.5928
35.168
2.一个圆柱的底面积是28.26 cm2,高是10 cm,它的体积是( )cm3。
第6课时 练习五
282.6
3.一个圆柱的底面半径是3 cm,高是10 cm,它的体积是( )cm3。
282.6
第6课时 练习五
4.一个圆柱的底面直径是6 cm,高是10 cm,它的体积是( )cm3。
282.6
第6课时 练习五
5.一个圆柱的底面周长是18.84 cm,高是10 cm,它的体积是( )cm3。
282.6
第6课时 练习五
6.求下面圆柱的表面积和体积。
表面积:3.14×(8÷2)2×2+3.14×8×11=376.8(m2)
体积:3.14×(8÷2)2×11=552.64(m3)
第6课时 练习五
7.把如下图所示的长方形绕长边旋转形成一个圆柱,求这个圆柱的体积。
3.14×22×3=37.68(cm3)
第6课时 练习五
8.下面圆柱形油桶的数据是从里面量得到的。这个油桶能装得下50 L花生油吗?
3.14×(4÷2)2×4=50.24(dm3)
50.24dm3=50.24L
50.24L>50L
这个油桶能装得下50L花生油。
第6课时 练习五
9.如下图所示,把左边袋子里的牛奶倒入右边的杯子中,牛奶的高度是多少厘米?(得数保留整数)
3.14×(8÷2)2=50.24(cm2)
350÷50.24≈7(cm)
第6课时 练习五
锦囊妙计 不论牛奶在袋子里还是杯子里,体积都不变。
快乐导航
圆锥的特征:圆锥的底面是个圆,侧面是一个曲面,圆锥的高只有1条。
第7课时 圆锥的认识
小试身手
1.下面的图形中,哪些是圆锥?在圆锥下面的括号里画“√”。
第7课时 圆锥的认识
√
√
2.旋转右边的直角三角形,可以形成一个圆锥。这个圆锥的底面半径是( )cm,高是( )cm。
2
3
第7课时 圆锥的认识
3.每课速算。
第7课时 圆锥的认识
4.选择题。(把正确答案的序号填在括号里)
(1)一个圆锥沿着它的高平均切成两块,切面一定是两个( )。
(A)扇形
(B)长方形
(C)等腰三角形
C
第7课时 圆锥的认识
(2)下面的图形中,只有一条高的是( )。
(A)平行四边形
(B)梯形
(C)圆锥
C
第7课时 圆锥的认识
(3)下面测量圆锥的高的方法中,正确的是( )。
第7课时 圆锥的认识
A
5.指出下面的圆锥的底面和侧面,画出圆锥的高。
第7课时 圆锥的认识
6.求下面圆锥的底面积。
3.14×22=12.56(cm2)
第7课时 圆锥的认识
7.如下图所示,一堵墙上有两个孔。
下面哪些立体图形可以从三角形孔穿过?哪些立体图形可以从圆形孔穿过?
只有圆锥可以从三角形孔穿过,圆柱、圆锥、球都可以从圆形孔穿过。
第7课时 圆锥的认识
锦囊妙计 分别从上面和侧面看这4个立体图形。
快乐导航
1.圆锥的体积是与它等底等高的圆柱的体积的三分之一。
2.字母公式:
3.应用圆锥体积公式解决问题时,要分析题目已知什么,求什么,然后根据公式求出体积,再进行解答。
第8课时 圆锥的体积
小试身手
1.要探究圆锥和圆柱体积之间的关系,下面三个圆锥中,应选图( )与圆柱进行对比。
第8课时 圆锥的体积
A
2.计算下面圆锥的体积。
第8课时 圆锥的体积
3.一个圆锥与一个圆柱等底等高,这个圆柱的体积是12 cm3,那么这个圆锥的体积是( )cm3。
4
第8课时 圆锥的体积
4.一个圆锥的底面积是20 cm2,它的高是9 cm,它的体积是( )cm3。
60
第8课时 圆锥的体积
5.一堆稻谷,近似于一个圆锥(如下图)。
(1)这堆稻谷大约有多少立方米?
第8课时 圆锥的体积
(2)如果每立方米的稻谷的质量大约是600 kg,那么这堆稻谷的质量大约是多少千克?
600×6.28=3768(kg)
第8课时 圆锥的体积
6.把一段长是3 dm、底面直径是2 dm的圆柱形木桩削成一个最大的圆锥,要削去多少立方分米的木头?
第8课时 圆锥的体积
锦囊妙计 削去的木头的体积是圆柱和圆锥的体积之差。
1.每课速算。
0.56÷0.7=
0.5×0.4=
0.36×1000=
0.36÷1000=
第9课时 练习六
0.8
0.2
360
0.00036
2.(1)一个圆锥的底面积是20 dm2,高是12 dm,这个圆锥的体积是( )dm3。
(2)一个圆柱的体积是300 cm3,与它等底等高的圆锥的体积是( )cm3。
(3)一个圆锥的体积是300 m3,与它等底等高的圆柱的体积是( )m3。
第9课时 练习六
80
100
900
3.判断题。(对的画“√”,错的画“×”)
(1)圆柱的体积一定比圆锥的体积大。
( )
(2)正方体、长方体、圆锥的体积都等于底面积×高。 ( )
(3)有两个等底等高的圆柱和圆锥,如果圆柱的体积是60 cm3,那么圆锥的体积是20 cm3。
( )
×
×
√
第9课时 练习六
4.计算下面圆锥的体积。
第9课时 练习六
5.根据下图数据算出这个冰激凌的体积。
第9课时 练习六
6.下面的帐篷占地面积大约是多少?所占的空间大约是多少?
第9课时 练习六
7.一个圆锥的底面直径是40 cm,从圆锥的顶点沿高切成两半(如下图),表面积增加了480 cm2。这个圆锥的体积是多少立方厘米?
第9课时 练习六
锦囊妙计 从圆锥的顶点沿高切成两半,切面是两个一样的等腰三角形。其中一个等腰三角形的底是圆锥的直径,高是圆锥的高。
第9课时 练习六
1.填表。
第10课时 练习七
图形 名称 半径 直径 高 表面积 体积
—
圆柱
2dm
4dm
75.36dm2
4dm
50.24dm3
圆锥
3cm
6cm
6cm
56.52dm3
2.下面的长方形纸分别沿长和宽卷成不同的圆柱形纸筒,如果给两个纸筒都配上相应的底面,那么
第10课时 练习七
12.56
78.8768
3.14
39.4384
(1)圆柱①的一个底面的面积是( )cm2,体积是( )cm3。
(2)圆柱②的一个底面的面积是( )cm2,体积是( )cm3。
3.把下面这堆沙以2 cm的厚度铺在宽8 m的路面上,能铺多长?
2cm=0.02m
18.84÷8÷0.02=117.75(m)
第10课时 练习七
4.美丽家园小区有个圆柱形游泳池。现在要给它的内壁和底面抹一层防水涂料,每平方米需0.6 kg涂料。
3.14×(40÷2)2+3.14×40×2=1507.2(m2)
0.6×1507.2=904.32(kg)
3.14×(40÷2)2×2=2512(m3)
第10课时 练习七
5.一个圆柱形水桶,从里面量,底面半径为20 cm,装有80 cm深的水。现将一个底面周长为62.8 cm的圆锥形铁块完全沉入水中,水比原来上升了 (水没有溢出)。这个圆锥形铁块的高是多少厘米?
第10课时 练习七
锦囊妙计 水上升部分的体积等于圆锥形铁块的体积。
单元知识清单(P25)
立体图形
特征 底面 两个底面完全相同,都是______ 一个底面,是______
侧面 沿高剪开,展开后是一个长方形或正方形 —
高 两个底面之间的距离,有_______条 顶点到底面圆心的距离,只有_______条
圆
圆
无数
1
面 积 底面积=圆周率×半径的平方, 字母公式:S=______; 侧面积=底面周长×高, 字母公式:S=________; 表面积=侧面积+底面积×2 —
体 积 物体所占空间的大小 底面积×高, 字母公式:V=______或V=________ 底面积×高×
字母公式:V=________或V=__________
续表
易错训练(P25)
1.算一算,比一比。
(1)一个圆柱,它的底面半径是2 cm,高是3 cm,它的体积是多少立方厘米?
(2)一个圆锥,它的底面半径是2 cm,高是3 cm,它的体积是多少立方厘米?
3.14×22×3=37.68(cm3)
(3)一个圆锥,它的底面半径是2 cm,高是9 cm,它的体积是多少立方厘米?
2.圆锥的体积一定是圆柱体积的 吗?圆锥的体积一定比圆柱的体积小吗?
3 圆柱与圆锥
数学配人教版
(六年级/下册)
第1课时 圆柱的认识和练习三
第2课时 圆柱的表面积
第3单元巩固练习
第3课时 练习四
第4课时 圆柱的体积(1)
第5课时 圆柱的体积(2)
第6课时 练习五
第7课时 圆锥的认识
第8课时 圆锥的体积
第9课时 练习六
第10课时 练习七
快乐导航
圆柱的特征:圆柱的上、下两个面是完全相同的两个圆,侧面是一个曲面,圆柱的高有无数条。
第1课时 圆柱的认识和练习三
把圆柱的侧面沿着一条高剪开,是一个长方形(或正方形)。这个长方形的长=圆柱底面的周长,宽=圆柱的高。
第1课时 圆柱的认识和练习三
小试身手
1.如下图,把下面的圆柱侧面展开后得到一个长方形。
第1课时 圆柱的认识和练习三
这个圆柱的高是( )cm,底面周长是( )cm。
3
5
2.下面的图形中,哪些是圆柱?在圆柱下面的括号里画“√”。
第1课时 圆柱的认识和练习三
√
√
3.下图的长方形ABCD,以AD边为轴旋转形成右边的圆柱。
这个圆柱的高是( )cm,底面半径是( )cm。
4
2
第1课时 圆柱的认识和练习三
4.将一个圆柱形罐头的侧面商标纸展开,得到一个长方形。
这个长方形的长是多少厘米?
3.14×8=25.12(cm)
第1课时 圆柱的认识和练习三
5.下面的长方形,和哪两个圆可以围成一个圆柱?为什么?(单位:cm)
因为圆③④的直径都为1cm,它们的周长都是3.14×1=3.14(cm),正好等于长方形的长,所以,这个长方形和圆③④可以围成一个圆柱。
第1课时 圆柱的认识和练习三
快乐导航
1.圆柱的侧面积=底面周长×高
2.圆柱的表面积=圆柱的侧面积+两个底面的面积
3.在解决圆柱表面积的实际应用问题时,有时只需要计算圆柱的一个底面,有时不需要计算圆柱的底面。解题时要根据实际情况进行计算。
第2课时 圆柱的表面积
小试身手
1.下面的两个饮料盒的侧面积分别是多少?
第2课时 圆柱的表面积
8×10×2+6×10×2=280(cm2)
3.14×8×10=251.2(cm2)
2.(1)一个圆柱的底面周长是3.14 cm,高是3 cm。它的侧面积是( )cm2。
(2)一个圆柱的底面直径是2 cm,高是3 cm。它的侧面积是( )cm2。
(3)一个圆柱的底面周长是3.14 cm,高是3 cm。它的一个底面的面积是( )cm2。
(4)一个圆柱的底面直径是2 cm,高是3 cm。它的一个底面的面积是( )cm2。
9.42
18.84
0.785
3.14
第2课时 圆柱的表面积
3.计算下面圆柱的表面积。
3.14×52=78.5(cm2)
2×3.14×5×12=376.8(cm2)
78.5×2+376.8=533.8(cm2)
第2课时 圆柱的表面积
4.做一个无盖的圆柱形铁皮水桶,底面直径为4 dm,高为 5 dm,至少需要多少平方分米的铁皮?
3.14×(4÷2)2=12.56(dm2)
3.14×4×5=62.8(dm2)
12.56+62.8=75.36(dm2)
第2课时 圆柱的表面积
1.求下面各圆柱的表面积。(单位:dm)
第3课时 练习四
3.14×(5÷2)2×2+3.14×5×20=353.25(dm2)
1.求下面各圆柱的表面积。(单位:dm)
第3课时 练习四
3.14×102×2+2×3.14×10×4=879.2(dm2)
2.以下是三个同学量出的某品牌茶叶罐的外包装数据,请你分别根据这三组数据计算出这个茶叶罐的表面积。
张丽:底面周长为25.12 cm,高为10 cm。
李亮:底面直径为8 cm,高为10 cm。
刘芳:底面半径为4 cm,高为10 cm。
第3课时 练习四
张丽:25.12÷3.14=8(cm),
3.14×(8÷2)2×2+3.14×8×10=351.68(cm2)
李亮:3.14×(8÷2)2×2+3.14×8×10=351.68(cm2)
刘芳:3.14×42×2+2×3.14×4×10=351.68(cm2)
3.把一根圆柱形木料如下图那样截成2段,得到2个小圆柱。那么这2个小圆柱的表面积之和与原圆柱形木料的表面积相比,( )。
(A)表面积增加
(B)表面积减少
(C)表面积不变
A
第3课时 练习四
4.一根圆柱形的通风管,直径是30 cm,长1 m。制作这样的一根通风管至少需要多少平方米的铁皮?
30cm=0.3m
3.14×0.3×1=0.942(m2)
第3课时 练习四
5.如右图,把一根圆柱形木料沿底面直径垂直切开,它的一半的表面积是多少平方厘米?
锦囊妙计 圆柱形木料的一半的表面积并不是原来圆柱形木料表面积的一半。
第3课时 练习四
上底和下底可以拼成一个圆,面积是
3.14×(20÷2)2=314(cm2)。
侧面由一个曲面和一个长方形组成,曲面的面积是3.14×20×30÷2=942(cm2),长方形的面积是20×30=600(cm2)。
整个图形的表面积是314+942+600=1856(cm2)。
第3课时 练习四
快乐导航
1.圆柱的体积计算公式推导如下:
圆柱的体积(容积)用含有字母的式子表示是V=Sh或V=πr2h。
第4课时 圆柱的体积(1)
2.在计算圆柱形容器的容积时,数据要从容器里面测量得到。
第4课时 圆柱的体积(1)
小试身手
1.下面长方体的体积是( )cm3,正方体的体积是( )cm3。
第4课时 圆柱的体积(1)
300
125
2.右边圆柱的体积是( )cm3。
75.36
第4课时 圆柱的体积(1)
3.计算下面各圆柱的体积。(单位:cm)
3.14×(4÷2)2×6=75.36(cm3)
第4课时 圆柱的体积(1)
3.计算下面各圆柱的体积。(单位:cm)
3.14×62×2=226.08(cm3)
第4课时 圆柱的体积(1)
4.一个圆柱形桶,从里面量,它的底面半径是1.5 dm,高是6 dm。这个圆柱形桶的容积是多少升?
3.14×1.52×6=42.39(dm3)
42.39dm3=42.39L
第4课时 圆柱的体积(1)
5.这根圆柱形木料最多能做多少个柜子?
3.14×0.32×5÷0.09=15.7(个)
最多能做15个柜子。
第4课时 圆柱的体积(1)
6.如下图所示,数据是从里面测量的。
3.14×(6÷2)2×10=282.6(cm3)
282.6cm3=282.6mL
282.6mL<300mL
这个罐子不能装下300mL的橙汁。
第4课时 圆柱的体积(1)
快乐导航
根据体积不变的特点,把不规则图形转化为圆柱求体积。
第5课时 圆柱的体积(2)
第5课时 圆柱的体积(2)
小试身手
1.下图所示的瓶子是不规则图形,请你分步算出它的容积。
(1)
3.14×(6÷2)2 ×10=282.6(cm3)
282.6cm3=282.6mL
(2)该瓶子上面无水部分的容积是多少毫升?
第5课时 圆柱的体积(2)
3.14×(6÷2)2×8=226.08(cm3 )
226.08 cm3 =226.08 mL
(3)该瓶子的容积是多少毫升?
第5课时 圆柱的体积(2)
282.6+226.08=508.68(mL)
2.一个装满水的圆柱形水杯,从里面量的数据如下图所示。
3.14×(10÷2)2×(10-6)=314(cm3)
314cm3=314mL
第5课时 圆柱的体积(2)
3.有一种饮料瓶的容积是600 mL。现在瓶中装有一些饮料,瓶子正放时饮料高度为20 cm,倒放时空余部分的高度为5 cm。瓶子中有饮料多少毫升?
600÷(20+5)×20=480(mL)
第5课时 圆柱的体积(2)
锦囊妙计 瓶子的容积600 mL相当于饮料的体积加上一个5 cm高的圆柱的体积,也就是(20+5)cm高的圆柱的体积。
1.一个圆柱形蓄水池,从外面量的底面半径是2.2 m,高是3 m。从里面量的底面半径是2 m,高是2.8 m。这个蓄水池的占地面积是( )m2,它所占的空间是( )m3,它最多能装水( )m3。
第6课时 练习五
15.1976
45.5928
35.168
2.一个圆柱的底面积是28.26 cm2,高是10 cm,它的体积是( )cm3。
第6课时 练习五
282.6
3.一个圆柱的底面半径是3 cm,高是10 cm,它的体积是( )cm3。
282.6
第6课时 练习五
4.一个圆柱的底面直径是6 cm,高是10 cm,它的体积是( )cm3。
282.6
第6课时 练习五
5.一个圆柱的底面周长是18.84 cm,高是10 cm,它的体积是( )cm3。
282.6
第6课时 练习五
6.求下面圆柱的表面积和体积。
表面积:3.14×(8÷2)2×2+3.14×8×11=376.8(m2)
体积:3.14×(8÷2)2×11=552.64(m3)
第6课时 练习五
7.把如下图所示的长方形绕长边旋转形成一个圆柱,求这个圆柱的体积。
3.14×22×3=37.68(cm3)
第6课时 练习五
8.下面圆柱形油桶的数据是从里面量得到的。这个油桶能装得下50 L花生油吗?
3.14×(4÷2)2×4=50.24(dm3)
50.24dm3=50.24L
50.24L>50L
这个油桶能装得下50L花生油。
第6课时 练习五
9.如下图所示,把左边袋子里的牛奶倒入右边的杯子中,牛奶的高度是多少厘米?(得数保留整数)
3.14×(8÷2)2=50.24(cm2)
350÷50.24≈7(cm)
第6课时 练习五
锦囊妙计 不论牛奶在袋子里还是杯子里,体积都不变。
快乐导航
圆锥的特征:圆锥的底面是个圆,侧面是一个曲面,圆锥的高只有1条。
第7课时 圆锥的认识
小试身手
1.下面的图形中,哪些是圆锥?在圆锥下面的括号里画“√”。
第7课时 圆锥的认识
√
√
2.旋转右边的直角三角形,可以形成一个圆锥。这个圆锥的底面半径是( )cm,高是( )cm。
2
3
第7课时 圆锥的认识
3.每课速算。
第7课时 圆锥的认识
4.选择题。(把正确答案的序号填在括号里)
(1)一个圆锥沿着它的高平均切成两块,切面一定是两个( )。
(A)扇形
(B)长方形
(C)等腰三角形
C
第7课时 圆锥的认识
(2)下面的图形中,只有一条高的是( )。
(A)平行四边形
(B)梯形
(C)圆锥
C
第7课时 圆锥的认识
(3)下面测量圆锥的高的方法中,正确的是( )。
第7课时 圆锥的认识
A
5.指出下面的圆锥的底面和侧面,画出圆锥的高。
第7课时 圆锥的认识
6.求下面圆锥的底面积。
3.14×22=12.56(cm2)
第7课时 圆锥的认识
7.如下图所示,一堵墙上有两个孔。
下面哪些立体图形可以从三角形孔穿过?哪些立体图形可以从圆形孔穿过?
只有圆锥可以从三角形孔穿过,圆柱、圆锥、球都可以从圆形孔穿过。
第7课时 圆锥的认识
锦囊妙计 分别从上面和侧面看这4个立体图形。
快乐导航
1.圆锥的体积是与它等底等高的圆柱的体积的三分之一。
2.字母公式:
3.应用圆锥体积公式解决问题时,要分析题目已知什么,求什么,然后根据公式求出体积,再进行解答。
第8课时 圆锥的体积
小试身手
1.要探究圆锥和圆柱体积之间的关系,下面三个圆锥中,应选图( )与圆柱进行对比。
第8课时 圆锥的体积
A
2.计算下面圆锥的体积。
第8课时 圆锥的体积
3.一个圆锥与一个圆柱等底等高,这个圆柱的体积是12 cm3,那么这个圆锥的体积是( )cm3。
4
第8课时 圆锥的体积
4.一个圆锥的底面积是20 cm2,它的高是9 cm,它的体积是( )cm3。
60
第8课时 圆锥的体积
5.一堆稻谷,近似于一个圆锥(如下图)。
(1)这堆稻谷大约有多少立方米?
第8课时 圆锥的体积
(2)如果每立方米的稻谷的质量大约是600 kg,那么这堆稻谷的质量大约是多少千克?
600×6.28=3768(kg)
第8课时 圆锥的体积
6.把一段长是3 dm、底面直径是2 dm的圆柱形木桩削成一个最大的圆锥,要削去多少立方分米的木头?
第8课时 圆锥的体积
锦囊妙计 削去的木头的体积是圆柱和圆锥的体积之差。
1.每课速算。
0.56÷0.7=
0.5×0.4=
0.36×1000=
0.36÷1000=
第9课时 练习六
0.8
0.2
360
0.00036
2.(1)一个圆锥的底面积是20 dm2,高是12 dm,这个圆锥的体积是( )dm3。
(2)一个圆柱的体积是300 cm3,与它等底等高的圆锥的体积是( )cm3。
(3)一个圆锥的体积是300 m3,与它等底等高的圆柱的体积是( )m3。
第9课时 练习六
80
100
900
3.判断题。(对的画“√”,错的画“×”)
(1)圆柱的体积一定比圆锥的体积大。
( )
(2)正方体、长方体、圆锥的体积都等于底面积×高。 ( )
(3)有两个等底等高的圆柱和圆锥,如果圆柱的体积是60 cm3,那么圆锥的体积是20 cm3。
( )
×
×
√
第9课时 练习六
4.计算下面圆锥的体积。
第9课时 练习六
5.根据下图数据算出这个冰激凌的体积。
第9课时 练习六
6.下面的帐篷占地面积大约是多少?所占的空间大约是多少?
第9课时 练习六
7.一个圆锥的底面直径是40 cm,从圆锥的顶点沿高切成两半(如下图),表面积增加了480 cm2。这个圆锥的体积是多少立方厘米?
第9课时 练习六
锦囊妙计 从圆锥的顶点沿高切成两半,切面是两个一样的等腰三角形。其中一个等腰三角形的底是圆锥的直径,高是圆锥的高。
第9课时 练习六
1.填表。
第10课时 练习七
图形 名称 半径 直径 高 表面积 体积
—
圆柱
2dm
4dm
75.36dm2
4dm
50.24dm3
圆锥
3cm
6cm
6cm
56.52dm3
2.下面的长方形纸分别沿长和宽卷成不同的圆柱形纸筒,如果给两个纸筒都配上相应的底面,那么
第10课时 练习七
12.56
78.8768
3.14
39.4384
(1)圆柱①的一个底面的面积是( )cm2,体积是( )cm3。
(2)圆柱②的一个底面的面积是( )cm2,体积是( )cm3。
3.把下面这堆沙以2 cm的厚度铺在宽8 m的路面上,能铺多长?
2cm=0.02m
18.84÷8÷0.02=117.75(m)
第10课时 练习七
4.美丽家园小区有个圆柱形游泳池。现在要给它的内壁和底面抹一层防水涂料,每平方米需0.6 kg涂料。
3.14×(40÷2)2+3.14×40×2=1507.2(m2)
0.6×1507.2=904.32(kg)
3.14×(40÷2)2×2=2512(m3)
第10课时 练习七
5.一个圆柱形水桶,从里面量,底面半径为20 cm,装有80 cm深的水。现将一个底面周长为62.8 cm的圆锥形铁块完全沉入水中,水比原来上升了 (水没有溢出)。这个圆锥形铁块的高是多少厘米?
第10课时 练习七
锦囊妙计 水上升部分的体积等于圆锥形铁块的体积。
单元知识清单(P25)
立体图形
特征 底面 两个底面完全相同,都是______ 一个底面,是______
侧面 沿高剪开,展开后是一个长方形或正方形 —
高 两个底面之间的距离,有_______条 顶点到底面圆心的距离,只有_______条
圆
圆
无数
1
面 积 底面积=圆周率×半径的平方, 字母公式:S=______; 侧面积=底面周长×高, 字母公式:S=________; 表面积=侧面积+底面积×2 —
体 积 物体所占空间的大小 底面积×高, 字母公式:V=______或V=________ 底面积×高×
字母公式:V=________或V=__________
续表
易错训练(P25)
1.算一算,比一比。
(1)一个圆柱,它的底面半径是2 cm,高是3 cm,它的体积是多少立方厘米?
(2)一个圆锥,它的底面半径是2 cm,高是3 cm,它的体积是多少立方厘米?
3.14×22×3=37.68(cm3)
(3)一个圆锥,它的底面半径是2 cm,高是9 cm,它的体积是多少立方厘米?
2.圆锥的体积一定是圆柱体积的 吗?圆锥的体积一定比圆柱的体积小吗?
