正方形[下学期]
图片预览



文档简介
课件20张PPT。正方形1. 正方形的定义
由正方形的定义可知,
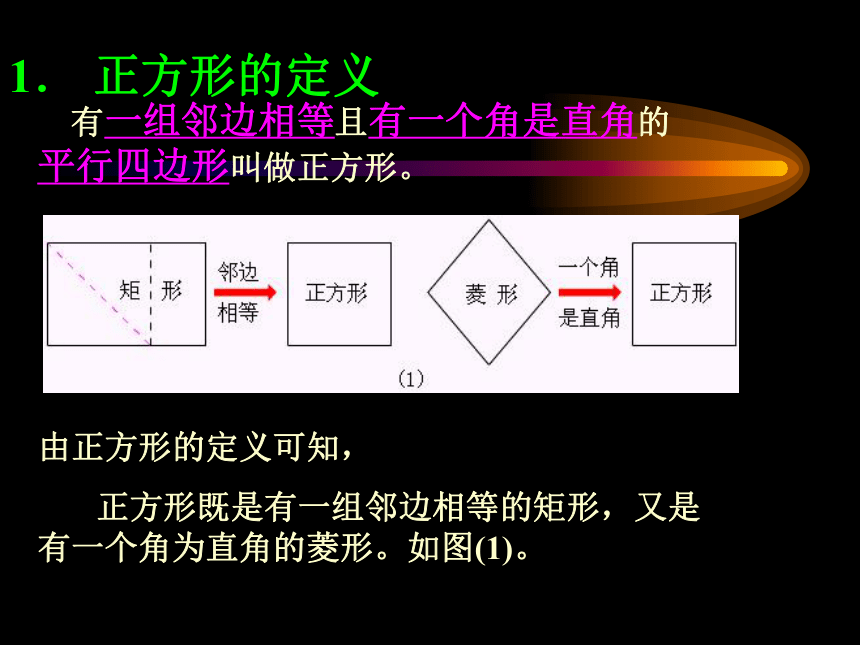
正方形既是有一组邻边相等的矩形,又是 有一个角为直角的菱形。如图(1)。 有一组邻边相等且有一个角是直角的平行四边形叫做正方形。
2. 正方形的性质 因为正方形既是特殊的矩形。又是特殊的菱形。因此正方形既具有矩形的性质,又具有菱形的性质。 正方形性质定理1:
正方形的四个角都是直角。
正方形的四条边都相等。 此外正方形还有:对边平行;内角和为360°的性质。 正方形性质定理2:
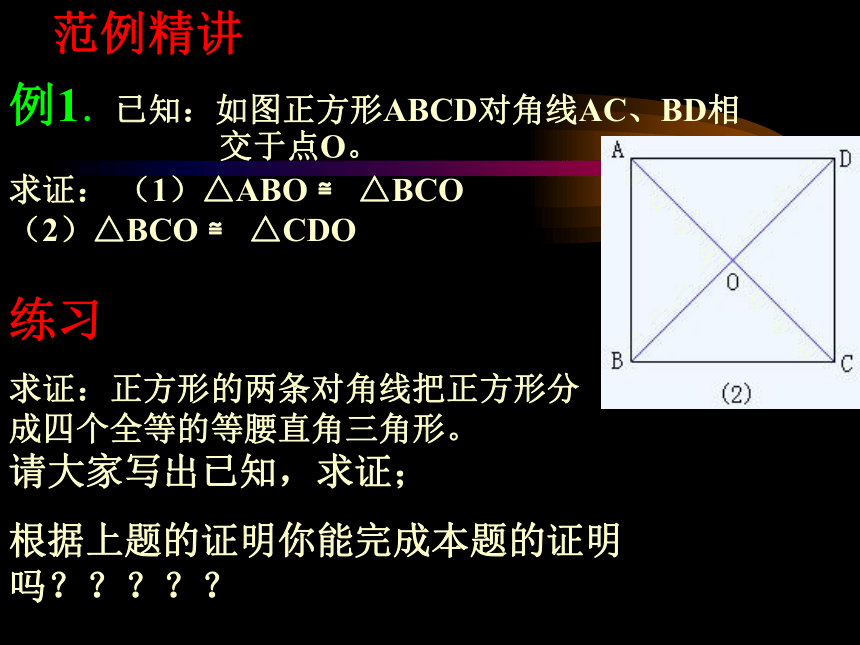
正方形的两条对角线相等,并且互相垂直平 分,且每条对角线平分一组对角。 0D:我的文档左信举j2040600.swf范例精讲 例1.已知:如图正方形ABCD对角线AC、BD相
请大家写出已知,求证;
根据上题的证明你能完成本题的证明吗?????
求证: (1)△ABO ≌ △BCO (2)△BCO ≌ △CDO 交于点O。练习
求证:正方形的两条对角线把正方形分 成四个全等的等腰直角三角形。
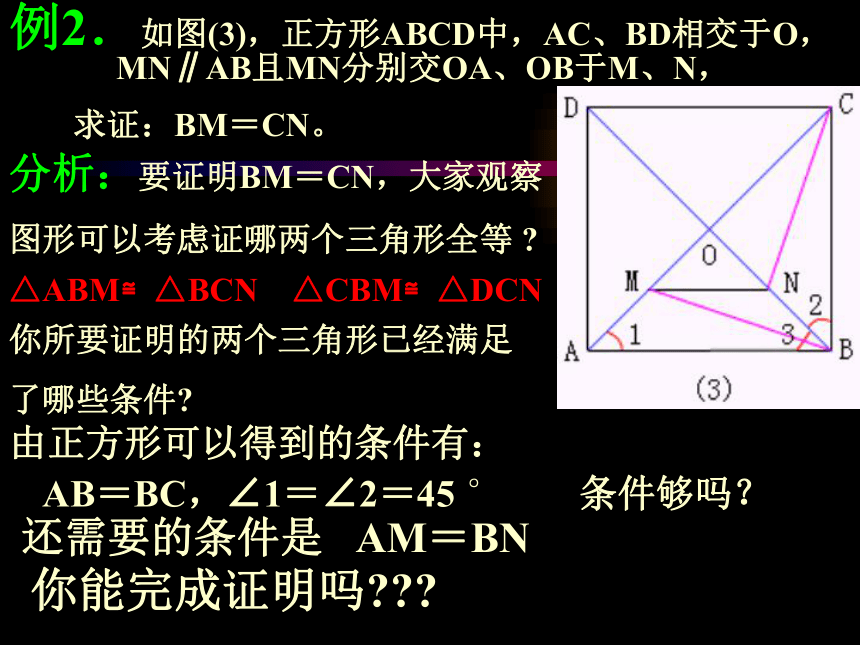
例2.如图(3),正方形ABCD中,AC、BD相交于O,
分析:要证明BM=CN,大家观察
图形可以考虑证哪两个三角形全等 ?
MN∥AB且MN分别交OA、OB于M、N,求证:BM=CN。
你能完成证明吗???
AB=BC,∠1=∠2=45 ° 条件够吗? 还需要的条件是 AM=BN
△ABM≌△BCN △CBM≌△DCN
你所要证明的两个三角形已经满足
了哪些条件?
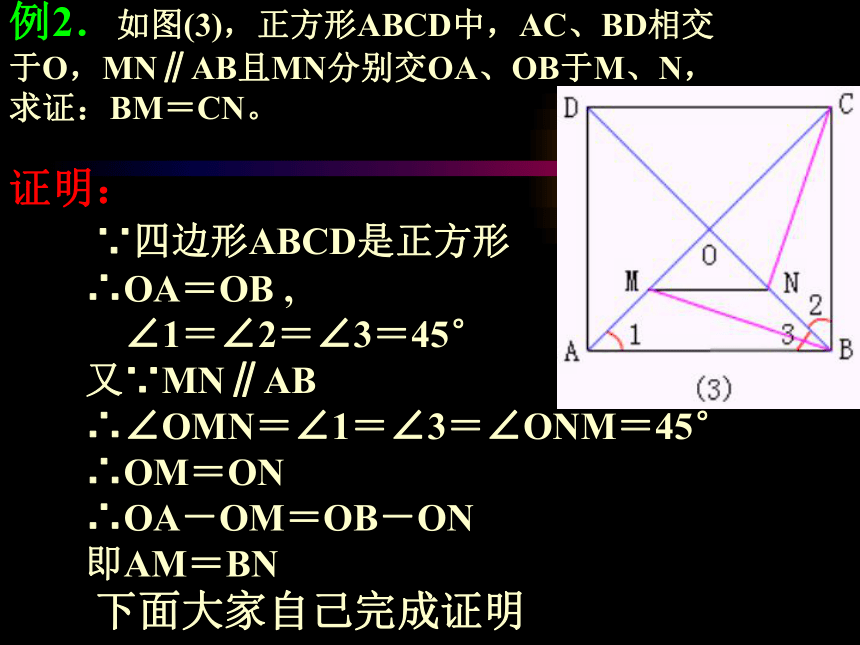
由正方形可以得到的条件有: 例2.如图(3),正方形ABCD中,AC、BD相交于O,MN∥AB且MN分别交OA、OB于M、N,求证:BM=CN。 证明:
∵四边形ABCD是正方形 ∴OA=OB ,
∠1=∠2=∠3=45° 又∵MN∥AB
∴∠OMN=∠1=∠3=∠ONM=45° ∴OM=ON ∴OA-OM=OB-ON 即AM=BN 下面大家自己完成证明 练习1.
已知:正方形ABCD对角线AC、BD相 交于点O,且AB=acm,如图(2)。
求:AC的长及正方形的面积S。 练习2.
已知:在正方形ABCD中,对角线AC、
BD相交于点O,且AC=6cm,如图
求:正方形的面积S。
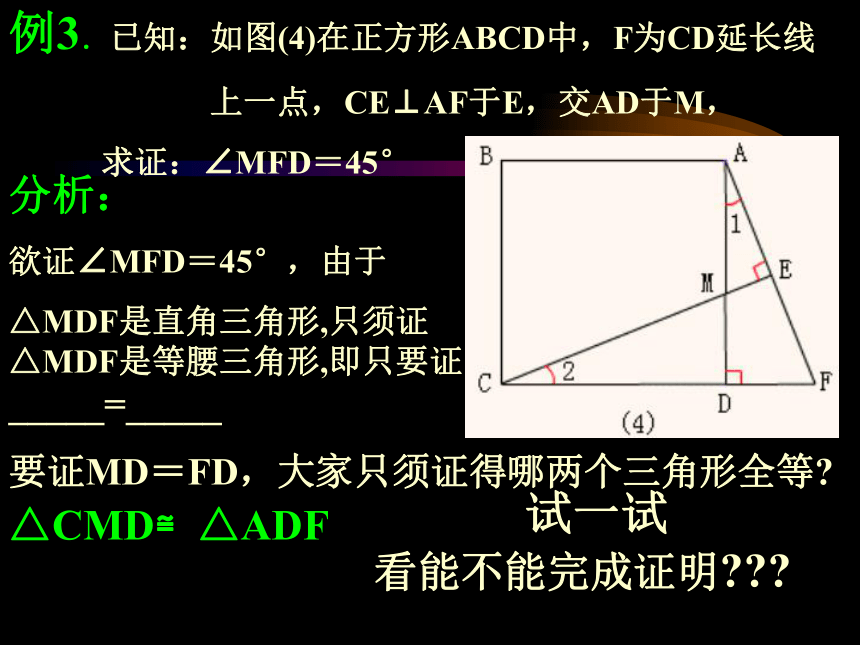
例3.已知:如图(4)在正方形ABCD中,F为CD延长线
上一点,CE⊥AF于E,交AD于M,
求证:∠MFD=45° 分析:
欲证∠MFD=45°,由于
△MDF是直角三角形,只须证△MDF是等腰三角形,即只要证 _____=_____要证MD=FD,大家只须证得哪两个三角形全等?
试一试
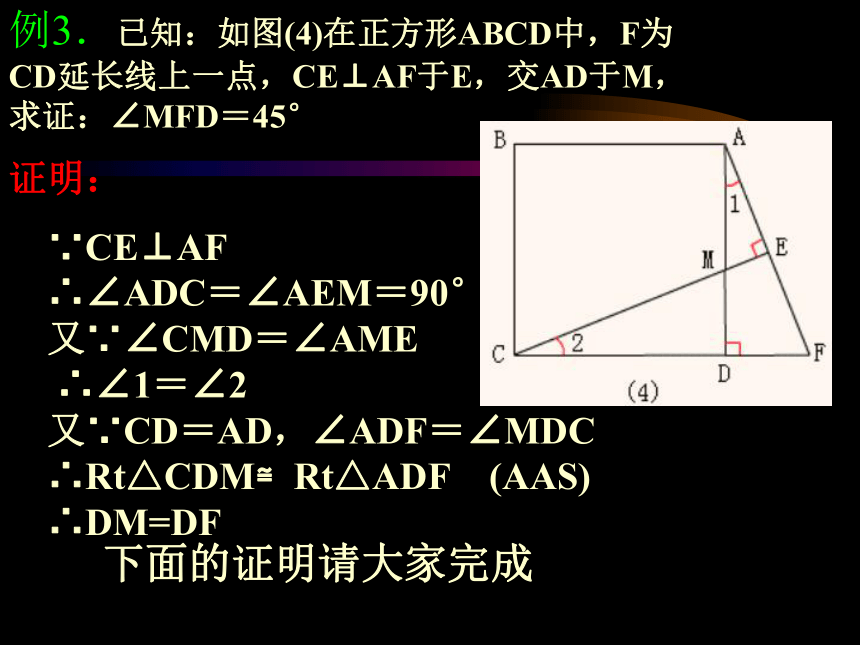
看能不能完成证明???△CMD≌△ADF例3.已知:如图(4)在正方形ABCD中,F为CD延长线上一点,CE⊥AF于E,交AD于M, 求证:∠MFD=45° 证明:
∵CE⊥AF ∴∠ADC=∠AEM=90° 又∵∠CMD=∠AME ∴∠1=∠2 又∵CD=AD,∠ADF=∠MDC ∴Rt△CDM≌Rt△ADF (AAS) ∴DM=DF
下面的证明请大家完成
练习.如图(5),在AB上取一点C,以AC、BC为正方形的一边在同一侧作正方形AEDC和BCFG连结AF、BD延长BD交AF于H。 求证:(1) △ACF≌△DCB
(2) BH⊥AF
证明:
例4.如图(6),△ABC的外面作正方形ABDE和ACFG,连结BG、CE,交点为N。 求证:∠CEA=∠ABG 分析:欲证∠CEA=∠ABG,
大家想一想证明两个角相等的方法,
你有办法了吗???通过自己的努力,看能不能解决问题?
证明:∵四边形ABDE和四边形ACFG是正方形。 ∴AE=AB AG=AC ∠1=∠2=90° 又∵∠EAC=∠1+∠BAC=90°+∠BAC ∠BAG=∠2+∠BAC=90°+∠BAC ∴∠EAC=∠BAG ∴△AEC≌△ABG (SAS)
∴∠CEA=∠ABG 3.图形之间的内在联系你还记得这个图形反映的结论吗?依次连接任意四边形各边中点所成的四边形是平行四边形.依次连接正方形各边中点所成的四边形是一个怎样的图形呢?先猜一猜,再证明.改变四边形的形状后,.对角线具有的关系(对角线相等,对角线垂直)决定了各中点所成四边形的形状.因此原四边形对角线的关系是关键.依次连接对角线垂直的四边形各边中点所成的四边形是一个矩形依次连接对角线相等的四边形各边中点所成的四边形是一个菱形填空:
1.顺次连接任意四边形四边中点得到_______________.
2.顺次连接对角线相等的四边形四边中点得到_____________.(如:连接矩形、等腰梯形的四边中点都得到菱形。)3.顺次连接对角线互相垂直的四边形四边中点得到___________.(如:顺次连接菱形的四边中点得到矩形.)平行四边形菱形矩形习题 已知:如图,A,B,C,D四家工厂分别坐落在正方形城镇的四个角上.仓库P和Q分别位于AD和DC上,且PD=QC.
证明:两条直路BP=AQ,且BP⊥AQ.想一想,做一做驶向胜利的彼岸在右图中,ABCDXA表示一条环行高速公路,X表示一座水库,B,C表示两个大市镇.已知ABCD是一个正方形,XAD表示是一个等边三角形.假如政府要铺设两条输水管XB和XC,从水库向B,C两个市镇供水,那么这两条水管的夹角(即∠BXC)是多少度?习题 1.如图,四边形ABCD是正方形,△ABC是等边三角形.
求:∠θ的度数.2.已知:如图,四个小朋友分别站在正方形ABCD的四条边的点A1,B1,C1,D1处,并且AA1=BB1=CC1=DD1,那么四个小朋友分别所站点为顶点的四边形A1B1C1D1是一个怎样的图形?请证明你的结论. 3.已知:如图,四边形ABCD是一个正方形,E是BC延长线上的一个点,且AC=EC.
求:∠DAE的度数.这
堂
课
你
学
到
了
什
么?回味无穷
正方形既是有一组邻边相等的矩形,又是 有一个角为直角的菱形。如图(1)。 有一组邻边相等且有一个角是直角的平行四边形叫做正方形。
2. 正方形的性质 因为正方形既是特殊的矩形。又是特殊的菱形。因此正方形既具有矩形的性质,又具有菱形的性质。 正方形性质定理1:
正方形的四个角都是直角。
正方形的四条边都相等。 此外正方形还有:对边平行;内角和为360°的性质。 正方形性质定理2:
正方形的两条对角线相等,并且互相垂直平 分,且每条对角线平分一组对角。 0D:我的文档左信举j2040600.swf范例精讲 例1.已知:如图正方形ABCD对角线AC、BD相
请大家写出已知,求证;
根据上题的证明你能完成本题的证明吗?????
求证: (1)△ABO ≌ △BCO (2)△BCO ≌ △CDO 交于点O。练习
求证:正方形的两条对角线把正方形分 成四个全等的等腰直角三角形。
例2.如图(3),正方形ABCD中,AC、BD相交于O,
分析:要证明BM=CN,大家观察
图形可以考虑证哪两个三角形全等 ?
MN∥AB且MN分别交OA、OB于M、N,求证:BM=CN。
你能完成证明吗???
AB=BC,∠1=∠2=45 ° 条件够吗? 还需要的条件是 AM=BN
△ABM≌△BCN △CBM≌△DCN
你所要证明的两个三角形已经满足
了哪些条件?
由正方形可以得到的条件有: 例2.如图(3),正方形ABCD中,AC、BD相交于O,MN∥AB且MN分别交OA、OB于M、N,求证:BM=CN。 证明:
∵四边形ABCD是正方形 ∴OA=OB ,
∠1=∠2=∠3=45° 又∵MN∥AB
∴∠OMN=∠1=∠3=∠ONM=45° ∴OM=ON ∴OA-OM=OB-ON 即AM=BN 下面大家自己完成证明 练习1.
已知:正方形ABCD对角线AC、BD相 交于点O,且AB=acm,如图(2)。
求:AC的长及正方形的面积S。 练习2.
已知:在正方形ABCD中,对角线AC、
BD相交于点O,且AC=6cm,如图
求:正方形的面积S。
例3.已知:如图(4)在正方形ABCD中,F为CD延长线
上一点,CE⊥AF于E,交AD于M,
求证:∠MFD=45° 分析:
欲证∠MFD=45°,由于
△MDF是直角三角形,只须证△MDF是等腰三角形,即只要证 _____=_____要证MD=FD,大家只须证得哪两个三角形全等?
试一试
看能不能完成证明???△CMD≌△ADF例3.已知:如图(4)在正方形ABCD中,F为CD延长线上一点,CE⊥AF于E,交AD于M, 求证:∠MFD=45° 证明:
∵CE⊥AF ∴∠ADC=∠AEM=90° 又∵∠CMD=∠AME ∴∠1=∠2 又∵CD=AD,∠ADF=∠MDC ∴Rt△CDM≌Rt△ADF (AAS) ∴DM=DF
下面的证明请大家完成
练习.如图(5),在AB上取一点C,以AC、BC为正方形的一边在同一侧作正方形AEDC和BCFG连结AF、BD延长BD交AF于H。 求证:(1) △ACF≌△DCB
(2) BH⊥AF
证明:
例4.如图(6),△ABC的外面作正方形ABDE和ACFG,连结BG、CE,交点为N。 求证:∠CEA=∠ABG 分析:欲证∠CEA=∠ABG,
大家想一想证明两个角相等的方法,
你有办法了吗???通过自己的努力,看能不能解决问题?
证明:∵四边形ABDE和四边形ACFG是正方形。 ∴AE=AB AG=AC ∠1=∠2=90° 又∵∠EAC=∠1+∠BAC=90°+∠BAC ∠BAG=∠2+∠BAC=90°+∠BAC ∴∠EAC=∠BAG ∴△AEC≌△ABG (SAS)
∴∠CEA=∠ABG 3.图形之间的内在联系你还记得这个图形反映的结论吗?依次连接任意四边形各边中点所成的四边形是平行四边形.依次连接正方形各边中点所成的四边形是一个怎样的图形呢?先猜一猜,再证明.改变四边形的形状后,.对角线具有的关系(对角线相等,对角线垂直)决定了各中点所成四边形的形状.因此原四边形对角线的关系是关键.依次连接对角线垂直的四边形各边中点所成的四边形是一个矩形依次连接对角线相等的四边形各边中点所成的四边形是一个菱形填空:
1.顺次连接任意四边形四边中点得到_______________.
2.顺次连接对角线相等的四边形四边中点得到_____________.(如:连接矩形、等腰梯形的四边中点都得到菱形。)3.顺次连接对角线互相垂直的四边形四边中点得到___________.(如:顺次连接菱形的四边中点得到矩形.)平行四边形菱形矩形习题 已知:如图,A,B,C,D四家工厂分别坐落在正方形城镇的四个角上.仓库P和Q分别位于AD和DC上,且PD=QC.
证明:两条直路BP=AQ,且BP⊥AQ.想一想,做一做驶向胜利的彼岸在右图中,ABCDXA表示一条环行高速公路,X表示一座水库,B,C表示两个大市镇.已知ABCD是一个正方形,XAD表示是一个等边三角形.假如政府要铺设两条输水管XB和XC,从水库向B,C两个市镇供水,那么这两条水管的夹角(即∠BXC)是多少度?习题 1.如图,四边形ABCD是正方形,△ABC是等边三角形.
求:∠θ的度数.2.已知:如图,四个小朋友分别站在正方形ABCD的四条边的点A1,B1,C1,D1处,并且AA1=BB1=CC1=DD1,那么四个小朋友分别所站点为顶点的四边形A1B1C1D1是一个怎样的图形?请证明你的结论. 3.已知:如图,四边形ABCD是一个正方形,E是BC延长线上的一个点,且AC=EC.
求:∠DAE的度数.这
堂
课
你
学
到
了
什
么?回味无穷
