第18章 平行四边形 单元测试(含答案)
图片预览



文档简介
中小学教育资源及组卷应用平台
第18章 《平行四边形》单元测试
题号 一 二 三 总分
19 20 21 22 23 24
分数
一.选择题(每题3分,共30分)
1.在平行四边形ABCD中,∠A+∠C=100°,则∠D=( )
A.130° B.120° C.70° D.80°
2.现有长为5,5,7的三根木棍,要想钉一个平行四边形的木框,则选用的第四根木棍的长度为( )
A.5 B.7 C.2 D.12
3.如图,在平行四边形ABCD中,已知∠ODA=90°,AC=10cm,BD=6cm,则AD的长为( )
A.4cm B.5cm C.6cm D.8cm
4. 如图,将 ABCD沿对角线AC折叠,使点B落在点B′处.若∠1=∠2=44°,则∠B为( )
A. 66° B. 104° C. 114° D. 124°
5. 从等腰三角形底边上任一点分别作两腰的平行线,所成的平行四边形的周长等于这个等腰三角形的 ( )
A.周长 B.周长的一半 C.腰长 D.腰长的2倍
6.如图,在平行四边形ABCD中,下列各式不一定正确的是 ( )
A. B.C. D.
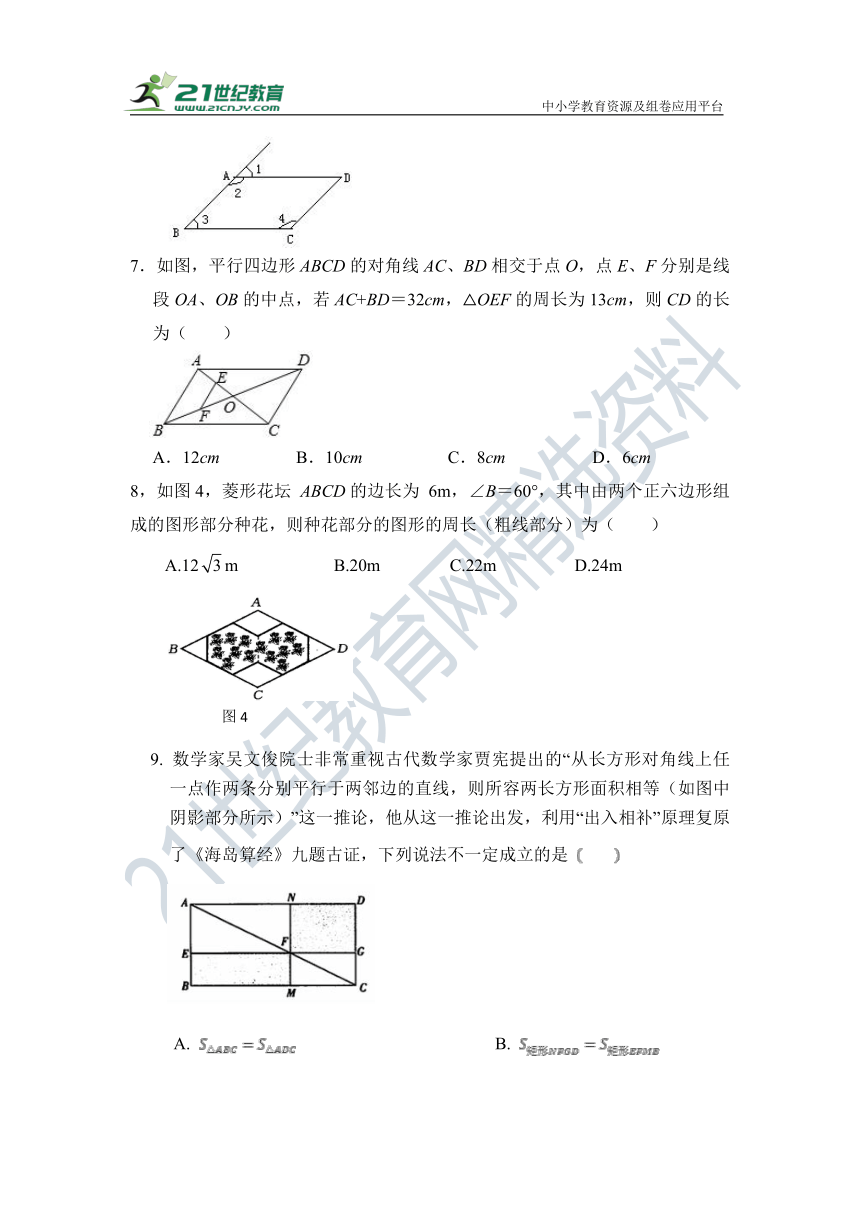
7.如图,平行四边形ABCD的对角线AC、BD相交于点O,点E、F分别是线段OA、OB的中点,若AC+BD=32cm,△OEF的周长为13cm,则CD的长为( )
A.12cm B.10cm C.8cm D.6cm
8,如图4,菱形花坛 ABCD的边长为 6m,∠B=60°,其中由两个正六边形组成的图形部分种花,则种花部分的图形的周长(粗线部分)为( )
A.12m B.20m C.22m D.24m
9. 数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图中阴影部分所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证,下列说法不一定成立的是
A. B.
C. D.
10. 如图,矩形 的对角线 , 相交于点 ,,,若 ,则四边形 的周长为
A. B. C. D.
二、填空题(每题3分,共30分)
11.在平行四边形ABCD中,∠C=∠B+∠D,则∠A= 度.
12.平行四边形ABCD中,AB、BC长分别为12和26,边AD与BC之间的距离为8,则AB与CD间的距离为 .
13.边长为a的正方形的对角线的长度为 .
14,如图10,已知AB∥DC,AE⊥DC,AE=12,BD=15,AC=20, 则梯形ABCD的面积为___.150
15,矩形纸片ABCD中,AD=4cm ,AB=10cm,按如图11方式折叠,使点B与点D重合,折痕为EF,则DE=___cm.
16,矩形ABCD中,对角线AC、BD相交于点O,∠AOB=2∠BOC.若AC=18cm,则AD=___cm.
17. 如图,过矩形 的对角线 上一点 ,分别作矩形两边的平行线 与 ,那么图中矩形 的面积 与矩形 的面积 的大小关系是 .(填“”“”或“”)
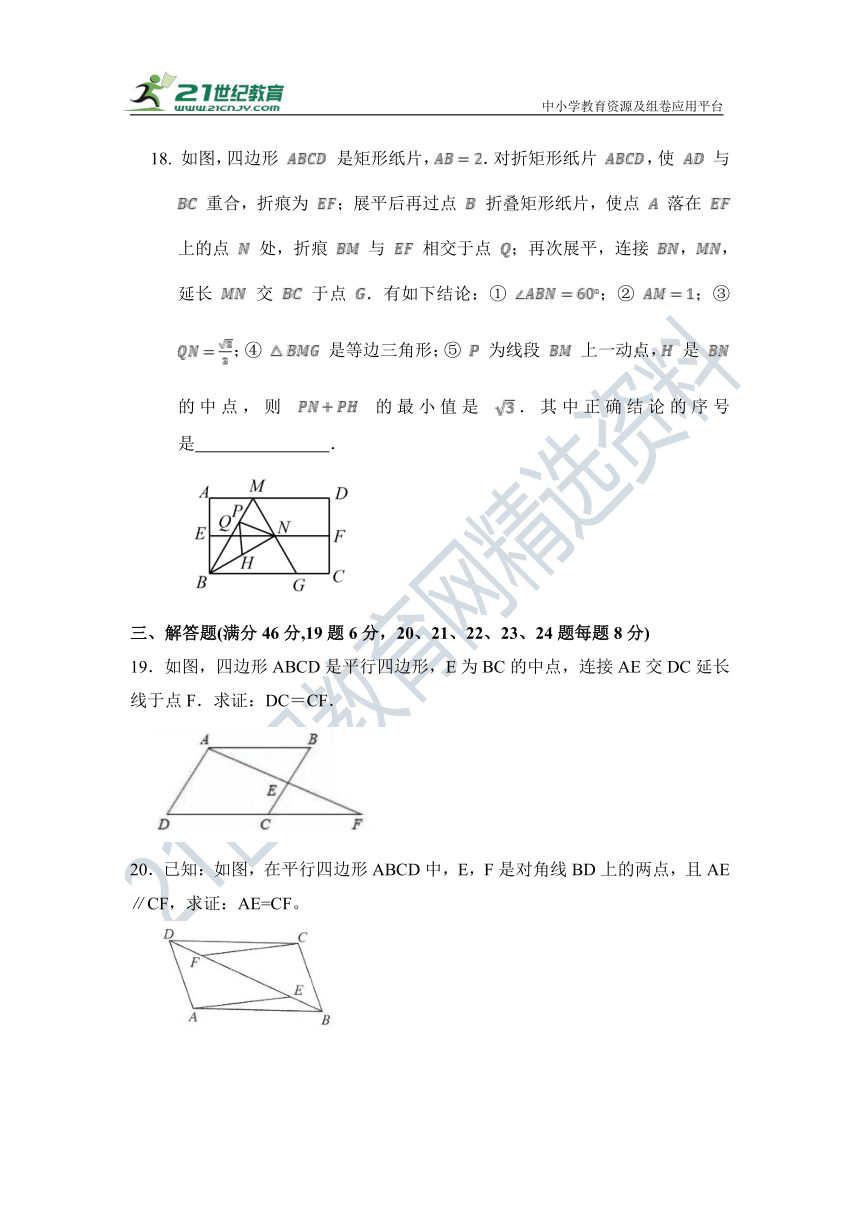
18. 如图,四边形 是矩形纸片,.对折矩形纸片 ,使 与 重合,折痕为 ;展平后再过点 折叠矩形纸片,使点 落在 上的点 处,折痕 与 相交于点 ;再次展平,连接 ,,延长 交 于点 .有如下结论:① ;② ;③ ;④ 是等边三角形;⑤ 为线段 上一动点, 是 的中点,则 的最小值是 .其中正确结论的序号是 .
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19.如图,四边形ABCD是平行四边形,E为BC的中点,连接AE交DC延长线于点F.求证:DC=CF.
20.已知:如图,在平行四边形ABCD中,E,F是对角线BD上的两点,且AE∥CF,求证:AE=CF。
21、如图,在平面直角坐标系中,四边形ABCD的四个顶点坐标分别为A(﹣3,﹣2),B(0,3),C(3,2),D(0,﹣3).四边形ABCD是不是平行四边形?请给出证明.
22、如图,直线a、b相交于点A,C、E分别是直线b、a上两点且BC⊥a,DE⊥b,点M、N是中点.求证:(1)DM=BM;(2)MN⊥BD 。
23.四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.
(1)求证:AM=AD+MC.
(2)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,试判断AM=AD+MC是否成立?若成立,请给出证明,若不成立,请说明理由;
24.已知四边形ABCD是正方形,点E是边BC上的任意一点,AE⊥EF,且直线EF交正方形外角的平分线CF于点F.
(1)如图1,求证:AE=EF;
(2)如图2,当AB=2,点E是边BC的中点时,请直接写出FC的长.
参考答案与解析
一、选择题(每题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 A B A C D D D B D C
二、填空题(每题3分,共24分)
11.在平行四边形ABCD中,∠C=∠B+∠D,则∠A= 120 度.
【分析】根据平行四边形的对边平行,对角相等,可得AD∥BC,∠B=∠D,∠A=∠C,易得∠C=2∠D,∠C+∠D=180°,解方程组即可求得.
【解答】解:∵四边形ABCD是平行四边形,
∴AD∥BC,∠B=∠D,∠A=∠C,
∴∠C=∠B+∠D=2∠D,∠C+∠D=180°,
∴∠A=∠C=120°,
故答案为:120.
【点评】此题考查了平行四边形的性质:平行四边形的对边平行;平行四边形的对角相等.解题的关键是数形结合思想的应用.
12.平行四边形ABCD中,AB、BC长分别为12和26,边AD与BC之间的距离为8,则AB与CD间的距离为 .
【分析】根据平行四边形的面积=AE×BC=CD×AF,即可求出AB与CD之间的距离.
【解答】解:如图,过点A作AE⊥BC于点E、AF⊥CD于点F.
由题意得,S四边形ABCD=AE×BC=CD×AF,
∵AB=12,BC=26,AE=8,
∴26×8=12×AF,
∴AF=,
即AB与CD间的距离为.
故答案是:.
【点评】本题考查了平行四边形的性质,解答本题的关键是熟练平行四边形的面积公式.
13.边长为a的正方形的对角线的长度为 a .
【分析】根据勾股定理即可求出边长为a的正方形的对角线的长度.
【解答】解:边长为a的正方形的对角线的长度为:
=a.
故答案为:a.
14.4﹣2或3. 解析:①当A′D=DC时,如图1,连接ED,
∵点E是AB的中点,AB=4,BC=4,四边形ABCD是矩形,
∴AD=BC=4,∠A=90°,∴DE==6,
∵将△AEF沿EF所在直线翻折,得到△A'EF,∴A′E=AE=2,
∵A′D=DC=AB=4,∴DE=A′E+A′D=6,
∴点E,A′,D三点共线,
∵∠A=90°,∴∠FA′E=∠FA′D=90°,
设AF=x,则A′F=x,FD=4-x,
在Rt△FA′D中,42+x2=(4-x)2,
解得:x=,∴FD=3;
②当A′D=A′C时,如图2,
∵A′D=A′C,∴点A′在线段CD的垂直平分线上,
∴点A′在线段AB的垂直平分线上,
∵点E是AB的中点,∴EA′是AB的垂直平分线,∴∠AEA′=90°,
∵将△AEF沿EF所在直线翻折,得到△A'EF,
∴∠A=∠EA′F=90°,AF=FA′,
∴四边形AEA′F是正方形,
∴AF=AE=2,∴DF=4-2,
故答案为:4-2或3.
14,150;
15,;
16,9;
17.
【解析】由矩形的特征可知,矩形的一条对角线把矩形分成面积相等的两个三角形,即 ,,,
所以 .
18. ①④⑤
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19.【答案】证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴,
∵E为BC的中点,
∴BE=CE
∴AB=CF,
∵AB=DC
∴DC=CF
20.【答案】证明:∵AE∥CF,
∠AEF=∠CFE,
180°-∠AEF=180°-∠CFE,
即∠AEB=∠DFC
∵四边形ABCD是平行四边形,
DC∥AB,DC=AB,
CDF=∠ABE,
在△CDF和△ABE中,
△CDF≌△ABE(AAS),AE=CF
21、解:四边形ABCD是平行四边形.
理由:∵A(﹣3,﹣2),B(0,3),C(3,2),D(0,﹣3),
∴AB=CD,BC=AD,
∴四边形ABCD是平行四边形.
22、
23.四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.
(1)求证:AM=AD+MC.
(2)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,试判断AM=AD+MC是否成立?若成立,请给出证明,若不成立,请说明理由;
【解答】解:(1)如图1,过点E作EF⊥AM于点F,连接EM,
∵四边形ABCD是正方形,∴∠D=∠C=90°,∴∠D=∠AFE,∵AE平分∠DAM,∴∠DAE=∠FAE,
AE=AE,∴△ADE≌△AFE(AAS),∴AD=AF,DE=FE,∵E是CD边的中点,∴DE=EC,
∴FE=EC,EM=EM,∴Rt△EFM≌Rt△ECM(HL),∴FM=MC.∴AM=AF+FM=AD+MC.
(2)AM=AD+MC成立,理由如下:如图2,过点E作EF⊥AM于点F,连接EM,
∵四边形ABCD是矩形,∴∠D=∠C=90°,∴∠D=∠AFE,∵AE平分∠DAM,∴∠DAE=∠FAE,
AE=AE,∴△ADE≌△AFE(AAS),∴AD=AF,DE=FE,∵E是CD边的中点,∴DE=EC,∴FE=EC,
EM=EM,∴Rt△EFM≌Rt△ECM(HL),∴FM=MC.∴AM=AF+FM=AD+MC.所以AM=AD+MC成立.
24.已知四边形ABCD是正方形,点E是边BC上的任意一点,AE⊥EF,且直线EF交正方形外角的平分线CF于点F.
(1)如图1,求证:AE=EF;
(2)如图2,当AB=2,点E是边BC的中点时,请直接写出FC的长.
【解答】(1)证明:如图1,在AB上截取BM=BE,连接ME,∵∠B=90°,∴∠BME=∠BEM=45°,
∴∠AME=135°=∠ECF,∵AB=BC,BM=BE,∴AM=EC,在△AME和△ECF中,
∴△AME≌△ECF(ASA),∴AE=EF;
(2)解:取AB中点M,连接EM,
∵AB=BC,E为BC中点,M为AB中点,∴AM=CE=BE,∴∠BME=∠BME=45°,
∴∠AME=135°=∠ECF,∵∠B=90°,∴∠BAE+∠AEB=90°,
∵∠AEF=90°,∴∠AEB+∠FEC=90°,∴∠BAE=∠FEC,在△AME和△ECF中,
∴△AME≌△ECF(ASA),∴EM=CF,
∵AB=2,点E是边BC的中点,∴BM=BE=1,∴CF=ME=.
图4
第18章 《平行四边形》单元测试
题号 一 二 三 总分
19 20 21 22 23 24
分数
一.选择题(每题3分,共30分)
1.在平行四边形ABCD中,∠A+∠C=100°,则∠D=( )
A.130° B.120° C.70° D.80°
2.现有长为5,5,7的三根木棍,要想钉一个平行四边形的木框,则选用的第四根木棍的长度为( )
A.5 B.7 C.2 D.12
3.如图,在平行四边形ABCD中,已知∠ODA=90°,AC=10cm,BD=6cm,则AD的长为( )
A.4cm B.5cm C.6cm D.8cm
4. 如图,将 ABCD沿对角线AC折叠,使点B落在点B′处.若∠1=∠2=44°,则∠B为( )
A. 66° B. 104° C. 114° D. 124°
5. 从等腰三角形底边上任一点分别作两腰的平行线,所成的平行四边形的周长等于这个等腰三角形的 ( )
A.周长 B.周长的一半 C.腰长 D.腰长的2倍
6.如图,在平行四边形ABCD中,下列各式不一定正确的是 ( )
A. B.C. D.
7.如图,平行四边形ABCD的对角线AC、BD相交于点O,点E、F分别是线段OA、OB的中点,若AC+BD=32cm,△OEF的周长为13cm,则CD的长为( )
A.12cm B.10cm C.8cm D.6cm
8,如图4,菱形花坛 ABCD的边长为 6m,∠B=60°,其中由两个正六边形组成的图形部分种花,则种花部分的图形的周长(粗线部分)为( )
A.12m B.20m C.22m D.24m
9. 数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图中阴影部分所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证,下列说法不一定成立的是
A. B.
C. D.
10. 如图,矩形 的对角线 , 相交于点 ,,,若 ,则四边形 的周长为
A. B. C. D.
二、填空题(每题3分,共30分)
11.在平行四边形ABCD中,∠C=∠B+∠D,则∠A= 度.
12.平行四边形ABCD中,AB、BC长分别为12和26,边AD与BC之间的距离为8,则AB与CD间的距离为 .
13.边长为a的正方形的对角线的长度为 .
14,如图10,已知AB∥DC,AE⊥DC,AE=12,BD=15,AC=20, 则梯形ABCD的面积为___.150
15,矩形纸片ABCD中,AD=4cm ,AB=10cm,按如图11方式折叠,使点B与点D重合,折痕为EF,则DE=___cm.
16,矩形ABCD中,对角线AC、BD相交于点O,∠AOB=2∠BOC.若AC=18cm,则AD=___cm.
17. 如图,过矩形 的对角线 上一点 ,分别作矩形两边的平行线 与 ,那么图中矩形 的面积 与矩形 的面积 的大小关系是 .(填“”“”或“”)
18. 如图,四边形 是矩形纸片,.对折矩形纸片 ,使 与 重合,折痕为 ;展平后再过点 折叠矩形纸片,使点 落在 上的点 处,折痕 与 相交于点 ;再次展平,连接 ,,延长 交 于点 .有如下结论:① ;② ;③ ;④ 是等边三角形;⑤ 为线段 上一动点, 是 的中点,则 的最小值是 .其中正确结论的序号是 .
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19.如图,四边形ABCD是平行四边形,E为BC的中点,连接AE交DC延长线于点F.求证:DC=CF.
20.已知:如图,在平行四边形ABCD中,E,F是对角线BD上的两点,且AE∥CF,求证:AE=CF。
21、如图,在平面直角坐标系中,四边形ABCD的四个顶点坐标分别为A(﹣3,﹣2),B(0,3),C(3,2),D(0,﹣3).四边形ABCD是不是平行四边形?请给出证明.
22、如图,直线a、b相交于点A,C、E分别是直线b、a上两点且BC⊥a,DE⊥b,点M、N是中点.求证:(1)DM=BM;(2)MN⊥BD 。
23.四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.
(1)求证:AM=AD+MC.
(2)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,试判断AM=AD+MC是否成立?若成立,请给出证明,若不成立,请说明理由;
24.已知四边形ABCD是正方形,点E是边BC上的任意一点,AE⊥EF,且直线EF交正方形外角的平分线CF于点F.
(1)如图1,求证:AE=EF;
(2)如图2,当AB=2,点E是边BC的中点时,请直接写出FC的长.
参考答案与解析
一、选择题(每题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 A B A C D D D B D C
二、填空题(每题3分,共24分)
11.在平行四边形ABCD中,∠C=∠B+∠D,则∠A= 120 度.
【分析】根据平行四边形的对边平行,对角相等,可得AD∥BC,∠B=∠D,∠A=∠C,易得∠C=2∠D,∠C+∠D=180°,解方程组即可求得.
【解答】解:∵四边形ABCD是平行四边形,
∴AD∥BC,∠B=∠D,∠A=∠C,
∴∠C=∠B+∠D=2∠D,∠C+∠D=180°,
∴∠A=∠C=120°,
故答案为:120.
【点评】此题考查了平行四边形的性质:平行四边形的对边平行;平行四边形的对角相等.解题的关键是数形结合思想的应用.
12.平行四边形ABCD中,AB、BC长分别为12和26,边AD与BC之间的距离为8,则AB与CD间的距离为 .
【分析】根据平行四边形的面积=AE×BC=CD×AF,即可求出AB与CD之间的距离.
【解答】解:如图,过点A作AE⊥BC于点E、AF⊥CD于点F.
由题意得,S四边形ABCD=AE×BC=CD×AF,
∵AB=12,BC=26,AE=8,
∴26×8=12×AF,
∴AF=,
即AB与CD间的距离为.
故答案是:.
【点评】本题考查了平行四边形的性质,解答本题的关键是熟练平行四边形的面积公式.
13.边长为a的正方形的对角线的长度为 a .
【分析】根据勾股定理即可求出边长为a的正方形的对角线的长度.
【解答】解:边长为a的正方形的对角线的长度为:
=a.
故答案为:a.
14.4﹣2或3. 解析:①当A′D=DC时,如图1,连接ED,
∵点E是AB的中点,AB=4,BC=4,四边形ABCD是矩形,
∴AD=BC=4,∠A=90°,∴DE==6,
∵将△AEF沿EF所在直线翻折,得到△A'EF,∴A′E=AE=2,
∵A′D=DC=AB=4,∴DE=A′E+A′D=6,
∴点E,A′,D三点共线,
∵∠A=90°,∴∠FA′E=∠FA′D=90°,
设AF=x,则A′F=x,FD=4-x,
在Rt△FA′D中,42+x2=(4-x)2,
解得:x=,∴FD=3;
②当A′D=A′C时,如图2,
∵A′D=A′C,∴点A′在线段CD的垂直平分线上,
∴点A′在线段AB的垂直平分线上,
∵点E是AB的中点,∴EA′是AB的垂直平分线,∴∠AEA′=90°,
∵将△AEF沿EF所在直线翻折,得到△A'EF,
∴∠A=∠EA′F=90°,AF=FA′,
∴四边形AEA′F是正方形,
∴AF=AE=2,∴DF=4-2,
故答案为:4-2或3.
14,150;
15,;
16,9;
17.
【解析】由矩形的特征可知,矩形的一条对角线把矩形分成面积相等的两个三角形,即 ,,,
所以 .
18. ①④⑤
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19.【答案】证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴,
∵E为BC的中点,
∴BE=CE
∴AB=CF,
∵AB=DC
∴DC=CF
20.【答案】证明:∵AE∥CF,
∠AEF=∠CFE,
180°-∠AEF=180°-∠CFE,
即∠AEB=∠DFC
∵四边形ABCD是平行四边形,
DC∥AB,DC=AB,
CDF=∠ABE,
在△CDF和△ABE中,
△CDF≌△ABE(AAS),AE=CF
21、解:四边形ABCD是平行四边形.
理由:∵A(﹣3,﹣2),B(0,3),C(3,2),D(0,﹣3),
∴AB=CD,BC=AD,
∴四边形ABCD是平行四边形.
22、
23.四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.
(1)求证:AM=AD+MC.
(2)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,试判断AM=AD+MC是否成立?若成立,请给出证明,若不成立,请说明理由;
【解答】解:(1)如图1,过点E作EF⊥AM于点F,连接EM,
∵四边形ABCD是正方形,∴∠D=∠C=90°,∴∠D=∠AFE,∵AE平分∠DAM,∴∠DAE=∠FAE,
AE=AE,∴△ADE≌△AFE(AAS),∴AD=AF,DE=FE,∵E是CD边的中点,∴DE=EC,
∴FE=EC,EM=EM,∴Rt△EFM≌Rt△ECM(HL),∴FM=MC.∴AM=AF+FM=AD+MC.
(2)AM=AD+MC成立,理由如下:如图2,过点E作EF⊥AM于点F,连接EM,
∵四边形ABCD是矩形,∴∠D=∠C=90°,∴∠D=∠AFE,∵AE平分∠DAM,∴∠DAE=∠FAE,
AE=AE,∴△ADE≌△AFE(AAS),∴AD=AF,DE=FE,∵E是CD边的中点,∴DE=EC,∴FE=EC,
EM=EM,∴Rt△EFM≌Rt△ECM(HL),∴FM=MC.∴AM=AF+FM=AD+MC.所以AM=AD+MC成立.
24.已知四边形ABCD是正方形,点E是边BC上的任意一点,AE⊥EF,且直线EF交正方形外角的平分线CF于点F.
(1)如图1,求证:AE=EF;
(2)如图2,当AB=2,点E是边BC的中点时,请直接写出FC的长.
【解答】(1)证明:如图1,在AB上截取BM=BE,连接ME,∵∠B=90°,∴∠BME=∠BEM=45°,
∴∠AME=135°=∠ECF,∵AB=BC,BM=BE,∴AM=EC,在△AME和△ECF中,
∴△AME≌△ECF(ASA),∴AE=EF;
(2)解:取AB中点M,连接EM,
∵AB=BC,E为BC中点,M为AB中点,∴AM=CE=BE,∴∠BME=∠BME=45°,
∴∠AME=135°=∠ECF,∵∠B=90°,∴∠BAE+∠AEB=90°,
∵∠AEF=90°,∴∠AEB+∠FEC=90°,∴∠BAE=∠FEC,在△AME和△ECF中,
∴△AME≌△ECF(ASA),∴EM=CF,
∵AB=2,点E是边BC的中点,∴BM=BE=1,∴CF=ME=.
图4
