第18章 平行四边形 单元测试(含答案)
文档属性
| 名称 | 第18章 平行四边形 单元测试(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 703.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-13 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第18章 《平行四边形》单元测试
题号 一 二 三 总分
19 20 21 22 23 24
分数
一.选择题(每题3分,共30分)
1.如图,在平行四边形ABCD中,∠ABC的平分线BE交AD于点E,∠AEB=25°,则∠A的大小为( )
A.100° B.120° C.130° D.150°
2.如图,已知平行四边形ABCD的面积为100,P为边CD上的任意一点,E,F分别是线段PA,PB的中点,则图中阴影部分的总面积为( )
A.30 B.25 C.22.5 D.50
3.如图所示,已知四边形ABCD中,R,P分别是BC,CD上的点,E,F分别是AP,RP的中点,当点P在CD上从C向D移动而点R不动时,那么下列结论成立的是( )
A.线段EF的长逐渐增大 B.线段EF的长逐渐减小
C.线段EF的长不变 D.线段EF的长与点P的位置有关
4. 如图,将 ABCD沿对角线AC折叠,使点B落在点B′处.若∠1=∠2=44°,则∠B为( )
A. 66° B. 104° C. 114° D. 124°
5. 从等腰三角形底边上任一点分别作两腰的平行线,所成的平行四边形的周长等于这个等腰三角形的 ( )
A.周长 B.周长的一半 C.腰长 D.腰长的2倍
6.如图,在平行四边形ABCD中,下列各式不一定正确的是 ( )
A. B.C. D.
7.如图,平行四边形ABCD的对角线AC、BD相交于点O,点E、F分别是线段OA、OB的中点,若AC+BD=32cm,△OEF的周长为13cm,则CD的长为( )
A.12cm B.10cm C.8cm D.6cm
8.已知四边形ABCD是平行四边形,下列结论①AB//CD;②AC=BD;③当AC=BD时,它是菱形;④当∠ABC=90°时,它是矩形.其中正确的是( )
A.①② B.①④ C.②③ D.③④
9.如图,在平行四边形ABCD中,AC平分∠DAB,∠DAB=60°,AD=4,则AC的长为( )
A.5 B. C.2 D.
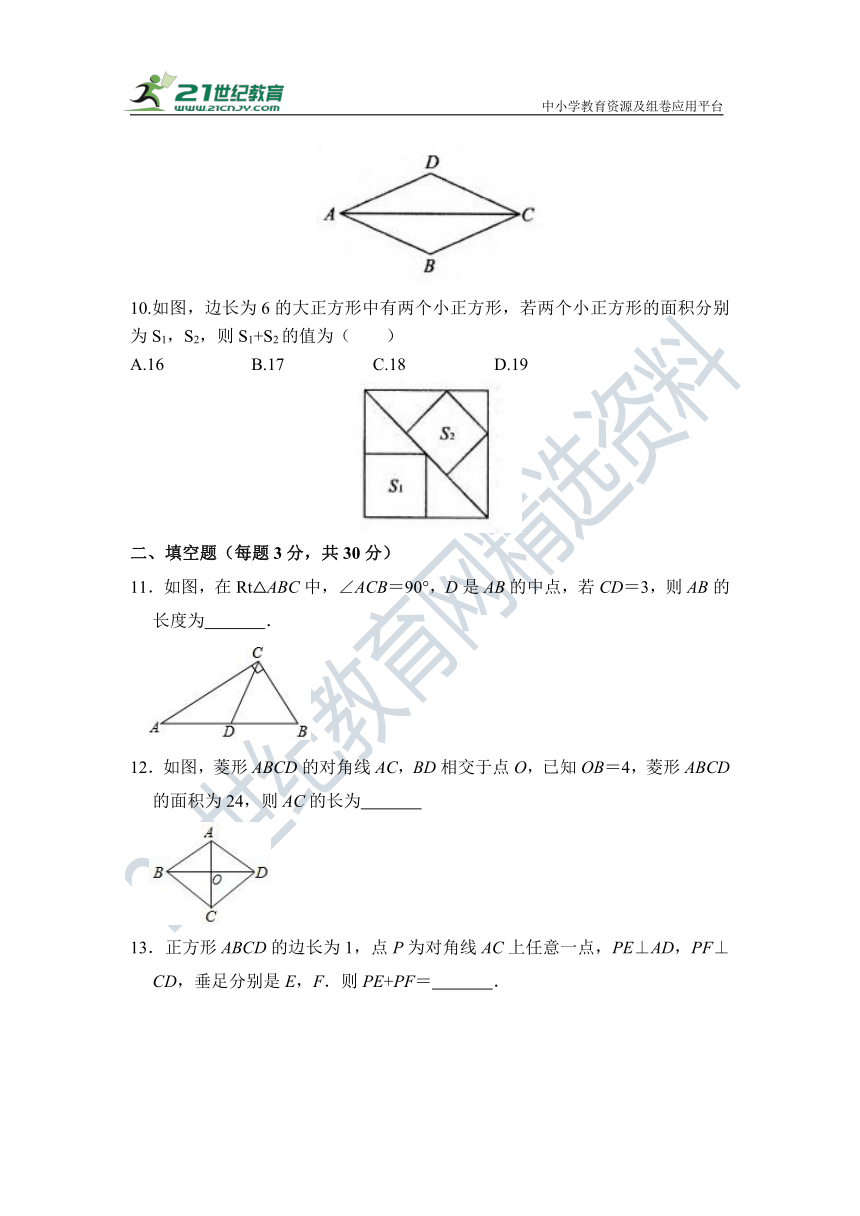
10.如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1,S2,则S1+S2的值为( )
A.16 B.17 C.18 D.19
二、填空题(每题3分,共30分)
11.如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,若CD=3,则AB的长度为 .
12.如图,菱形ABCD的对角线AC,BD相交于点O,已知OB=4,菱形ABCD的面积为24,则AC的长为
13.正方形ABCD的边长为1,点P为对角线AC上任意一点,PE⊥AD,PF⊥CD,垂足分别是E,F.则PE+PF= .
14,如图10,已知AB∥DC,AE⊥DC,AE=12,BD=15,AC=20, 则梯形ABCD的面积为___.150
15,矩形纸片ABCD中,AD=4cm ,AB=10cm,按如图11方式折叠,使点B与点D重合,折痕为EF,则DE=___cm.
16,矩形ABCD中,对角线AC、BD相交于点O,∠AOB=2∠BOC.若AC=18cm,则AD=___cm.
17.如图,在矩形ABCD中,AD=4,点E在边AD上,连接CE,以CE为边向右上方作正方形CEFG,作FH⊥AD,垂足为H,连接AF,当AE为 时,△AEF的面积最大.
18.如图,在矩形ABCD中,AB=,AD=3,E,F分别是边BC、AB上任意点,以线段EF为边,在EF上方作等边△EFG,取边EG的中点H,连接HC,则HC的最小值是 .
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
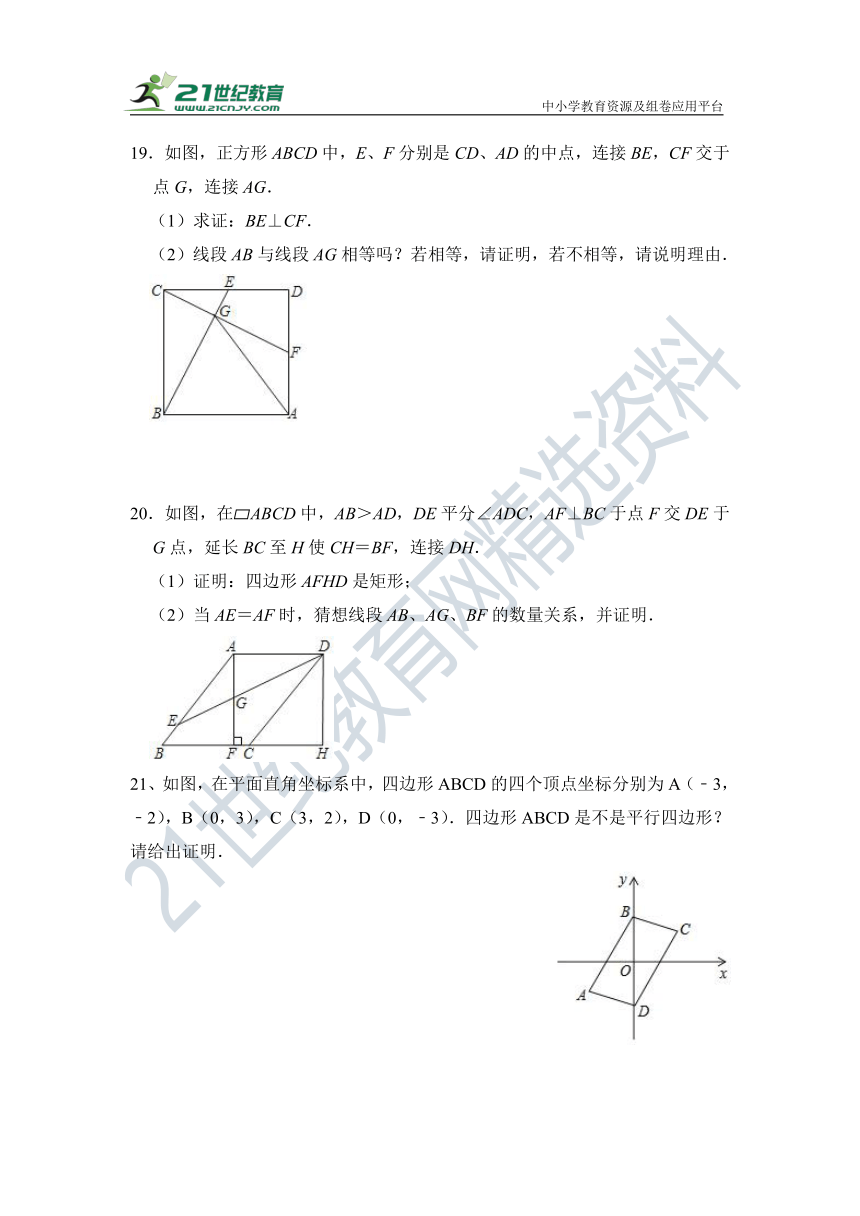
19.如图,正方形ABCD中,E、F分别是CD、AD的中点,连接BE,CF交于点G,连接AG.
(1)求证:BE⊥CF.
(2)线段AB与线段AG相等吗?若相等,请证明,若不相等,请说明理由.
20.如图,在 ABCD中,AB>AD,DE平分∠ADC,AF⊥BC于点F交DE于G点,延长BC至H使CH=BF,连接DH.
(1)证明:四边形AFHD是矩形;
(2)当AE=AF时,猜想线段AB、AG、BF的数量关系,并证明.
21、如图,在平面直角坐标系中,四边形ABCD的四个顶点坐标分别为A(﹣3,﹣2),B(0,3),C(3,2),D(0,﹣3).四边形ABCD是不是平行四边形?请给出证明.
22、如图,直线a、b相交于点A,C、E分别是直线b、a上两点且BC⊥a,DE⊥b,点M、N是中点.求证:(1)DM=BM;(2)MN⊥BD 。
23.如图,在Rt△ABC中,∠ACB=90°,D,E分别为AB,AC边的中点,连接DE并延长至点F,使得DE=EF,连接AF,CF.
(1)求证:四边形ADCF是菱形;
(2)若BC=8,AC=6,求四边形ABCF的周长.
24.两个长为2cm,宽为1cm的矩形摆放在直线上(如图①),CE=2cm,将矩形ABCD绕着点C顺时针旋转a角,将矩形EFGH绕着点E逆时针旋转相同的角度.
(1)当旋转到顶点D,H重合时(如图②),连接AE,CG,求证:△AED≌△GCD;
(2)当a=45°时(如图③),求证:四边形MHND为正方形.
参考答案与解析
一、选择题(每题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 C B C C D D D B D C
二、填空题(每题3分,共24分)
11. 6.
12. 6.
13. 1.
14.4﹣2或3. 解析:①当A′D=DC时,如图1,连接ED,
∵点E是AB的中点,AB=4,BC=4,四边形ABCD是矩形,
∴AD=BC=4,∠A=90°,∴DE==6,
∵将△AEF沿EF所在直线翻折,得到△A'EF,∴A′E=AE=2,
∵A′D=DC=AB=4,∴DE=A′E+A′D=6,
∴点E,A′,D三点共线,
∵∠A=90°,∴∠FA′E=∠FA′D=90°,
设AF=x,则A′F=x,FD=4-x,
在Rt△FA′D中,42+x2=(4-x)2,
解得:x=,∴FD=3;
②当A′D=A′C时,如图2,
∵A′D=A′C,∴点A′在线段CD的垂直平分线上,
∴点A′在线段AB的垂直平分线上,
∵点E是AB的中点,∴EA′是AB的垂直平分线,∴∠AEA′=90°,
∵将△AEF沿EF所在直线翻折,得到△A'EF,
∴∠A=∠EA′F=90°,AF=FA′,
∴四边形AEA′F是正方形,
∴AF=AE=2,∴DF=4-2,
故答案为:4-2或3.
14,150;
15,;
16,9;
17. 2.
18. .
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19.如图,正方形ABCD中,E、F分别是CD、AD的中点,连接BE,CF交于点G,连接AG.
(1)求证:BE⊥CF.
(2)线段AB与线段AG相等吗?若相等,请证明,若不相等,请说明理由.
【解答】(1)证明:∵四边形ABCD是正方形,∴AD=BC=CD,∠BCE=∠CDF=90°,
∵E、F是CD和AD的中点,∴CE=CD,DF=AD,∴CE=DF,
在△BCE和△CDF中,,∴△BCE≌△CDF(SAS),∴∠CBE=∠DCF,
∵∠BCG+∠DCF=90°,∴∠CBE+∠BCG=90°,∴∠BGC=90°,∴BE⊥CF;
(2)解:线段AB与线段AG相等;理由如下:延长CF交BA的延长线于点H,如图所示:
∵F是AD的中点,∴DF=AF,∵四边形ABCD是正方形,∴AB=CD,∠D=∠FAH=90°,
在△CDF和△HAF中,,∴△CDF≌△HAF(ASA),∴CD=AH,∴AB=AH,
∴A是BH中点,由(1)得:BE⊥CF,∴∠BGH=90°,∴AG=AB.
20.如图,在 ABCD中,AB>AD,DE平分∠ADC,AF⊥BC于点F交DE于G点,延长BC至H使CH=BF,连接DH.
(1)证明:四边形AFHD是矩形;
(2)当AE=AF时,猜想线段AB、AG、BF的数量关系,并证明.
【解答】(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,
∵CH=BF,∴FH=BC,∴AD=FH,∴四边形AFHD是平形四边形,
∵AF⊥BC,∴∠AFH=90°,∴平行四边形AFHD是矩形;
(2)猜想:AB=BF+AG,证明:如图,延长BF到M,使HM=AG,连接DM,
∵四边形ABCD是平行四边形,∴AB∥CD,∴∠1=∠2,
∵DE平分∠ADC,∴∠2=∠3,∴∠1=∠3,∴AE=AD,
∵AE=AF,∴AF=AD,四边形AFHD是正方形,∴AD=DH,∠GAD=∠DHM=90°,
在△DAG和△DHM中,∴△DAG≌△DHM(SAS),∴∠2=∠3=∠HDM,∠AGD=∠M,
∵AF∥DH,∴∠AGD=∠HDG=∠2+∠CDH=∠MDH+∠CDH,∴∠M=∠CDM,
∴CD=CM=CH+HM,∵BC=AD=FH,∴BC﹣CF=FH﹣CF,∴BF=CH,∵AB=CD,HM=AG,∴AB=BF+AG.
21、解:四边形ABCD是平行四边形.
理由:∵A(﹣3,﹣2),B(0,3),C(3,2),D(0,﹣3),
∴AB=CD,BC=AD,
∴四边形ABCD是平行四边形.
22、
23.(1)证明:∵点E是边AC的中点,
∴AE=EC.
又∵EF=DE,
∴四边形ADCF是平行四边形.
又∵点D,E分别是边AB,AC的中点,
∴DE是△ABC的中位线.∴DE//BC.
又∵∠ACB=90°,∴∠AED=90°.
∴AC⊥DF.
∴四边形ADCF是菱形.
(2)解:∵四边形ADCF是菱形.
∴CD=CF=AF=AD.
在Rt△ABC中,
∴AD=AB=5.∴CF=AF=5.
∴周长为:10+8+5+5=28.
24.证明:(1)∵AD=CD,ED=CD,∠ADC=∠GDE=90°,
∴∠ADC+∠CDE=∠GDE+∠CDE.
∴∠ADE=∠GDC.
在△AED和△GCD中,
∴△AED≌△GCD.(SAS)
(2)∵a=45°,
∴∠NCE=∠NEC=45°,CN=NE.
∴∠CNE=90°,∴∠DNH=90°.
∵∠D=∠H=90°,
∴四边形MHND是矩形.
∵CN=NE,∴DC-CN=EH-NE,
即DN=NH
∴矩形MHND是正方形.
25.解:(1)∵AB=10,PA=2t,∴BP=10-2t,
故答案为10-2t.
(2)当PB=DE时,四边形PDEB是平行四边形,
∴10-2t=5,∴t=2.5,
答:当t=2.5s时,四边形PDEB是平行四边形.
(3)存在.
①当EP=ED=5时,可得四边形DEPQ,四边形DEP'Q'是菱形,
作EH⊥AB于H.
在Rt△PEH中,∵PE=5,EH=BC=3,
∴,∴AP=1或AP'=9,
∴t=s或s时,可得四边形DEPQ,
四边形DEP'Q'是菱形.
②当DP"=DE时,可得四边形DEQ"P"是菱形,易知AP"=4,∴t=2,
综上所述,满足条件的1的值为s或2s或
第18章 《平行四边形》单元测试
题号 一 二 三 总分
19 20 21 22 23 24
分数
一.选择题(每题3分,共30分)
1.如图,在平行四边形ABCD中,∠ABC的平分线BE交AD于点E,∠AEB=25°,则∠A的大小为( )
A.100° B.120° C.130° D.150°
2.如图,已知平行四边形ABCD的面积为100,P为边CD上的任意一点,E,F分别是线段PA,PB的中点,则图中阴影部分的总面积为( )
A.30 B.25 C.22.5 D.50
3.如图所示,已知四边形ABCD中,R,P分别是BC,CD上的点,E,F分别是AP,RP的中点,当点P在CD上从C向D移动而点R不动时,那么下列结论成立的是( )
A.线段EF的长逐渐增大 B.线段EF的长逐渐减小
C.线段EF的长不变 D.线段EF的长与点P的位置有关
4. 如图,将 ABCD沿对角线AC折叠,使点B落在点B′处.若∠1=∠2=44°,则∠B为( )
A. 66° B. 104° C. 114° D. 124°
5. 从等腰三角形底边上任一点分别作两腰的平行线,所成的平行四边形的周长等于这个等腰三角形的 ( )
A.周长 B.周长的一半 C.腰长 D.腰长的2倍
6.如图,在平行四边形ABCD中,下列各式不一定正确的是 ( )
A. B.C. D.
7.如图,平行四边形ABCD的对角线AC、BD相交于点O,点E、F分别是线段OA、OB的中点,若AC+BD=32cm,△OEF的周长为13cm,则CD的长为( )
A.12cm B.10cm C.8cm D.6cm
8.已知四边形ABCD是平行四边形,下列结论①AB//CD;②AC=BD;③当AC=BD时,它是菱形;④当∠ABC=90°时,它是矩形.其中正确的是( )
A.①② B.①④ C.②③ D.③④
9.如图,在平行四边形ABCD中,AC平分∠DAB,∠DAB=60°,AD=4,则AC的长为( )
A.5 B. C.2 D.
10.如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1,S2,则S1+S2的值为( )
A.16 B.17 C.18 D.19
二、填空题(每题3分,共30分)
11.如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,若CD=3,则AB的长度为 .
12.如图,菱形ABCD的对角线AC,BD相交于点O,已知OB=4,菱形ABCD的面积为24,则AC的长为
13.正方形ABCD的边长为1,点P为对角线AC上任意一点,PE⊥AD,PF⊥CD,垂足分别是E,F.则PE+PF= .
14,如图10,已知AB∥DC,AE⊥DC,AE=12,BD=15,AC=20, 则梯形ABCD的面积为___.150
15,矩形纸片ABCD中,AD=4cm ,AB=10cm,按如图11方式折叠,使点B与点D重合,折痕为EF,则DE=___cm.
16,矩形ABCD中,对角线AC、BD相交于点O,∠AOB=2∠BOC.若AC=18cm,则AD=___cm.
17.如图,在矩形ABCD中,AD=4,点E在边AD上,连接CE,以CE为边向右上方作正方形CEFG,作FH⊥AD,垂足为H,连接AF,当AE为 时,△AEF的面积最大.
18.如图,在矩形ABCD中,AB=,AD=3,E,F分别是边BC、AB上任意点,以线段EF为边,在EF上方作等边△EFG,取边EG的中点H,连接HC,则HC的最小值是 .
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19.如图,正方形ABCD中,E、F分别是CD、AD的中点,连接BE,CF交于点G,连接AG.
(1)求证:BE⊥CF.
(2)线段AB与线段AG相等吗?若相等,请证明,若不相等,请说明理由.
20.如图,在 ABCD中,AB>AD,DE平分∠ADC,AF⊥BC于点F交DE于G点,延长BC至H使CH=BF,连接DH.
(1)证明:四边形AFHD是矩形;
(2)当AE=AF时,猜想线段AB、AG、BF的数量关系,并证明.
21、如图,在平面直角坐标系中,四边形ABCD的四个顶点坐标分别为A(﹣3,﹣2),B(0,3),C(3,2),D(0,﹣3).四边形ABCD是不是平行四边形?请给出证明.
22、如图,直线a、b相交于点A,C、E分别是直线b、a上两点且BC⊥a,DE⊥b,点M、N是中点.求证:(1)DM=BM;(2)MN⊥BD 。
23.如图,在Rt△ABC中,∠ACB=90°,D,E分别为AB,AC边的中点,连接DE并延长至点F,使得DE=EF,连接AF,CF.
(1)求证:四边形ADCF是菱形;
(2)若BC=8,AC=6,求四边形ABCF的周长.
24.两个长为2cm,宽为1cm的矩形摆放在直线上(如图①),CE=2cm,将矩形ABCD绕着点C顺时针旋转a角,将矩形EFGH绕着点E逆时针旋转相同的角度.
(1)当旋转到顶点D,H重合时(如图②),连接AE,CG,求证:△AED≌△GCD;
(2)当a=45°时(如图③),求证:四边形MHND为正方形.
参考答案与解析
一、选择题(每题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 C B C C D D D B D C
二、填空题(每题3分,共24分)
11. 6.
12. 6.
13. 1.
14.4﹣2或3. 解析:①当A′D=DC时,如图1,连接ED,
∵点E是AB的中点,AB=4,BC=4,四边形ABCD是矩形,
∴AD=BC=4,∠A=90°,∴DE==6,
∵将△AEF沿EF所在直线翻折,得到△A'EF,∴A′E=AE=2,
∵A′D=DC=AB=4,∴DE=A′E+A′D=6,
∴点E,A′,D三点共线,
∵∠A=90°,∴∠FA′E=∠FA′D=90°,
设AF=x,则A′F=x,FD=4-x,
在Rt△FA′D中,42+x2=(4-x)2,
解得:x=,∴FD=3;
②当A′D=A′C时,如图2,
∵A′D=A′C,∴点A′在线段CD的垂直平分线上,
∴点A′在线段AB的垂直平分线上,
∵点E是AB的中点,∴EA′是AB的垂直平分线,∴∠AEA′=90°,
∵将△AEF沿EF所在直线翻折,得到△A'EF,
∴∠A=∠EA′F=90°,AF=FA′,
∴四边形AEA′F是正方形,
∴AF=AE=2,∴DF=4-2,
故答案为:4-2或3.
14,150;
15,;
16,9;
17. 2.
18. .
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19.如图,正方形ABCD中,E、F分别是CD、AD的中点,连接BE,CF交于点G,连接AG.
(1)求证:BE⊥CF.
(2)线段AB与线段AG相等吗?若相等,请证明,若不相等,请说明理由.
【解答】(1)证明:∵四边形ABCD是正方形,∴AD=BC=CD,∠BCE=∠CDF=90°,
∵E、F是CD和AD的中点,∴CE=CD,DF=AD,∴CE=DF,
在△BCE和△CDF中,,∴△BCE≌△CDF(SAS),∴∠CBE=∠DCF,
∵∠BCG+∠DCF=90°,∴∠CBE+∠BCG=90°,∴∠BGC=90°,∴BE⊥CF;
(2)解:线段AB与线段AG相等;理由如下:延长CF交BA的延长线于点H,如图所示:
∵F是AD的中点,∴DF=AF,∵四边形ABCD是正方形,∴AB=CD,∠D=∠FAH=90°,
在△CDF和△HAF中,,∴△CDF≌△HAF(ASA),∴CD=AH,∴AB=AH,
∴A是BH中点,由(1)得:BE⊥CF,∴∠BGH=90°,∴AG=AB.
20.如图,在 ABCD中,AB>AD,DE平分∠ADC,AF⊥BC于点F交DE于G点,延长BC至H使CH=BF,连接DH.
(1)证明:四边形AFHD是矩形;
(2)当AE=AF时,猜想线段AB、AG、BF的数量关系,并证明.
【解答】(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,
∵CH=BF,∴FH=BC,∴AD=FH,∴四边形AFHD是平形四边形,
∵AF⊥BC,∴∠AFH=90°,∴平行四边形AFHD是矩形;
(2)猜想:AB=BF+AG,证明:如图,延长BF到M,使HM=AG,连接DM,
∵四边形ABCD是平行四边形,∴AB∥CD,∴∠1=∠2,
∵DE平分∠ADC,∴∠2=∠3,∴∠1=∠3,∴AE=AD,
∵AE=AF,∴AF=AD,四边形AFHD是正方形,∴AD=DH,∠GAD=∠DHM=90°,
在△DAG和△DHM中,∴△DAG≌△DHM(SAS),∴∠2=∠3=∠HDM,∠AGD=∠M,
∵AF∥DH,∴∠AGD=∠HDG=∠2+∠CDH=∠MDH+∠CDH,∴∠M=∠CDM,
∴CD=CM=CH+HM,∵BC=AD=FH,∴BC﹣CF=FH﹣CF,∴BF=CH,∵AB=CD,HM=AG,∴AB=BF+AG.
21、解:四边形ABCD是平行四边形.
理由:∵A(﹣3,﹣2),B(0,3),C(3,2),D(0,﹣3),
∴AB=CD,BC=AD,
∴四边形ABCD是平行四边形.
22、
23.(1)证明:∵点E是边AC的中点,
∴AE=EC.
又∵EF=DE,
∴四边形ADCF是平行四边形.
又∵点D,E分别是边AB,AC的中点,
∴DE是△ABC的中位线.∴DE//BC.
又∵∠ACB=90°,∴∠AED=90°.
∴AC⊥DF.
∴四边形ADCF是菱形.
(2)解:∵四边形ADCF是菱形.
∴CD=CF=AF=AD.
在Rt△ABC中,
∴AD=AB=5.∴CF=AF=5.
∴周长为:10+8+5+5=28.
24.证明:(1)∵AD=CD,ED=CD,∠ADC=∠GDE=90°,
∴∠ADC+∠CDE=∠GDE+∠CDE.
∴∠ADE=∠GDC.
在△AED和△GCD中,
∴△AED≌△GCD.(SAS)
(2)∵a=45°,
∴∠NCE=∠NEC=45°,CN=NE.
∴∠CNE=90°,∴∠DNH=90°.
∵∠D=∠H=90°,
∴四边形MHND是矩形.
∵CN=NE,∴DC-CN=EH-NE,
即DN=NH
∴矩形MHND是正方形.
25.解:(1)∵AB=10,PA=2t,∴BP=10-2t,
故答案为10-2t.
(2)当PB=DE时,四边形PDEB是平行四边形,
∴10-2t=5,∴t=2.5,
答:当t=2.5s时,四边形PDEB是平行四边形.
(3)存在.
①当EP=ED=5时,可得四边形DEPQ,四边形DEP'Q'是菱形,
作EH⊥AB于H.
在Rt△PEH中,∵PE=5,EH=BC=3,
∴,∴AP=1或AP'=9,
∴t=s或s时,可得四边形DEPQ,
四边形DEP'Q'是菱形.
②当DP"=DE时,可得四边形DEQ"P"是菱形,易知AP"=4,∴t=2,
综上所述,满足条件的1的值为s或2s或
