2023年中考数学三轮冲刺专题复习测试卷:二次函数图像与系数的关系(含答案)
文档属性
| 名称 | 2023年中考数学三轮冲刺专题复习测试卷:二次函数图像与系数的关系(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 156.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-13 21:46:26 | ||
图片预览

文档简介
2023年中考数学三轮冲刺专题复习测试卷:二次函数图像与系数的关系
一、单选题(共12题;共24分)
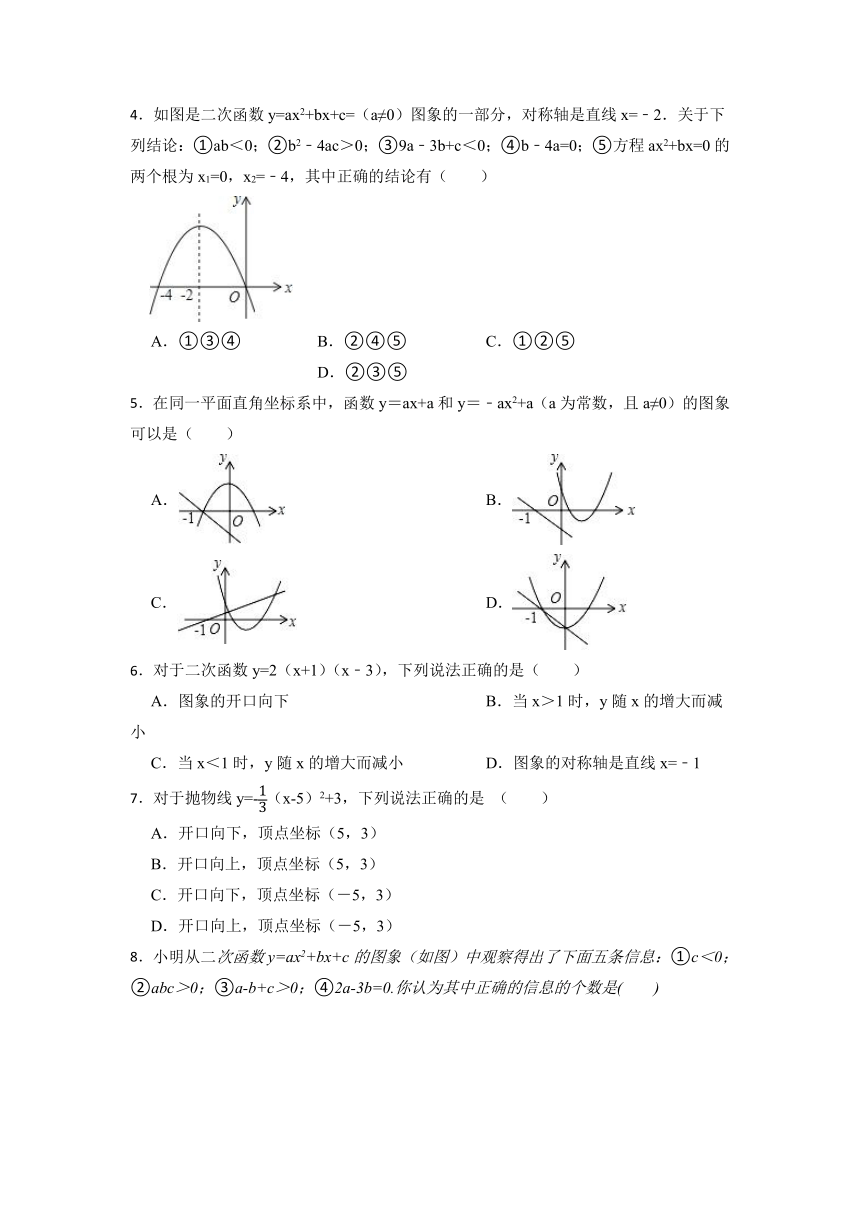
1.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;②b﹣a>c;③4a+2b+c>0;④3a>c;⑤a+b>m(am+b)(m≠1的实数),其中结论正确的有( )
A.①②③ B.②③⑤ C.②③④ D.③④⑤
2.在同一直角坐标系中,函数y=mx+m和y=﹣mx2+2x+2(m是常数,且m≠0)的图像可能是( )
A. B.
C. D.
3.函数与在同一直角坐标系中的大致图象可能是( )
A. B.
C. D.
4.如图是二次函数y=ax2+bx+c=(a≠0)图象的一部分,对称轴是直线x=﹣2.关于下列结论:①ab<0;②b2﹣4ac>0;③9a﹣3b+c<0;④b﹣4a=0;⑤方程ax2+bx=0的两个根为x1=0,x2=﹣4,其中正确的结论有( )
A.①③④ B.②④⑤ C.①②⑤ D.②③⑤
5.在同一平面直角坐标系中,函数y=ax+a和y=﹣ax2+a(a为常数,且a≠0)的图象可以是( )
A. B.
C. D.
6.对于二次函数y=2(x+1)(x﹣3),下列说法正确的是( )
A.图象的开口向下 B.当x>1时,y随x的增大而减小
C.当x<1时,y随x的增大而减小 D.图象的对称轴是直线x=﹣1
7.对于抛物线y=-(x-5)2+3,下列说法正确的是 ( )
A.开口向下,顶点坐标(5,3)
B.开口向上,顶点坐标(5,3)
C.开口向下,顶点坐标(-5,3)
D.开口向上,顶点坐标(-5,3)
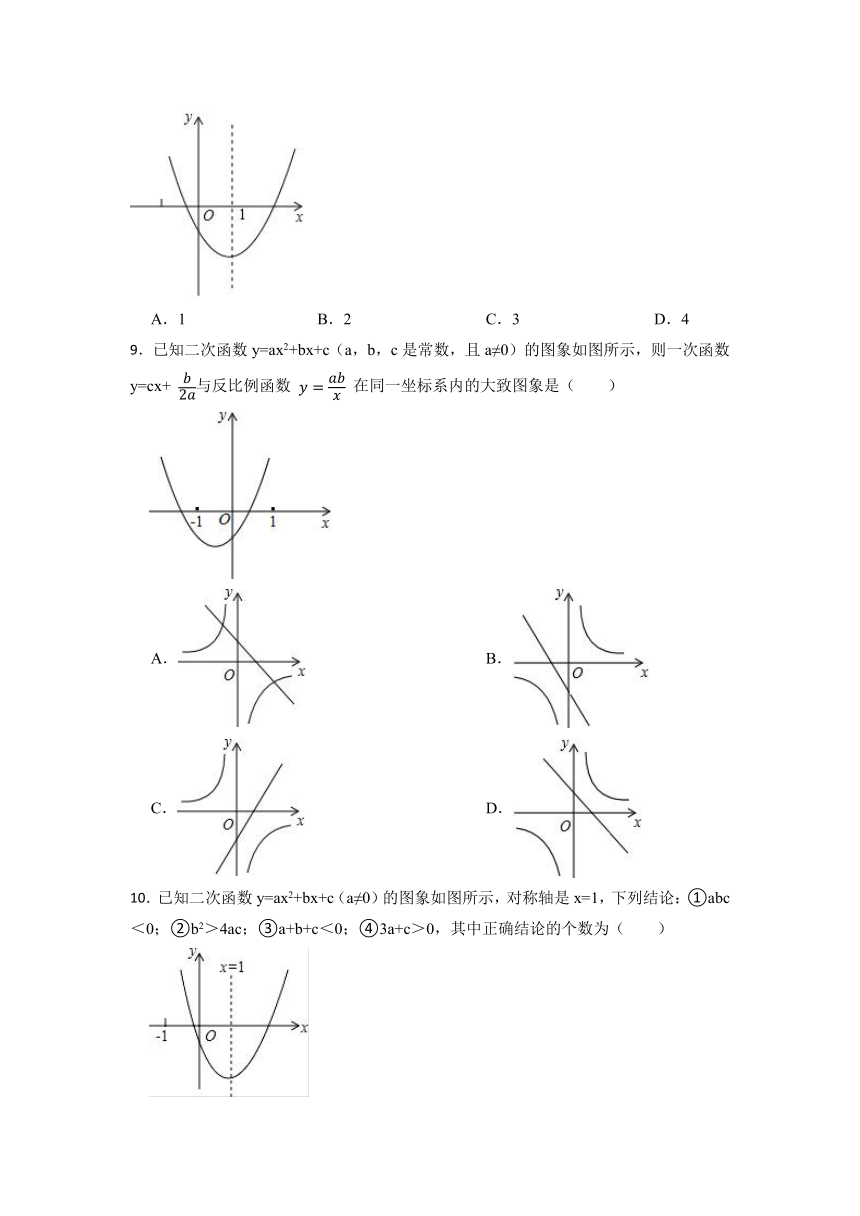
8.小明从二次函数y=ax2+bx+c的图象(如图)中观察得出了下面五条信息:①c<0;②abc>0;③a-b+c>0;④2a-3b=0.你认为其中正确的信息的个数是( )
A.1 B.2 C.3 D.4
9.已知二次函数y=ax2+bx+c(a,b,c是常数,且a≠0)的图象如图所示,则一次函数y=cx+ 与反比例函数 在同一坐标系内的大致图象是( )
A. B.
C. D.
10.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是x=1,下列结论:①abc<0;②b2>4ac;③a+b+c<0;④3a+c>0,其中正确结论的个数为( )
A.1个 B.2个 C.3个 D.4个
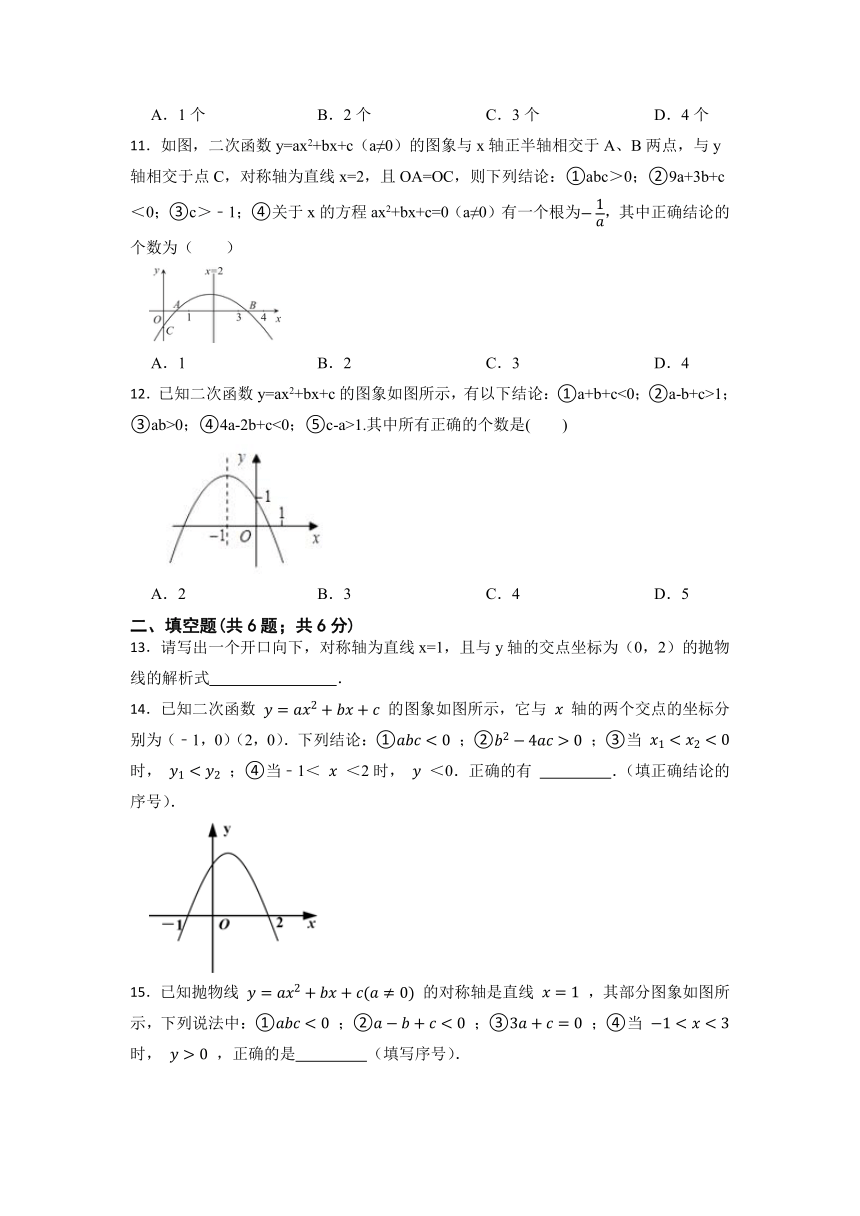
11.如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴正半轴相交于A、B两点,与y轴相交于点C,对称轴为直线x=2,且OA=OC,则下列结论:①abc>0;②9a+3b+c<0;③c>﹣1;④关于x的方程ax2+bx+c=0(a≠0)有一个根为,其中正确结论的个数为( )
A.1 B.2 C.3 D.4
12.已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:①a+b+c<0;②a-b+c>1;③ab>0;④4a-2b+c<0;⑤c-a>1.其中所有正确的个数是( )
A.2 B.3 C.4 D.5
二、填空题(共6题;共6分)
13.请写出一个开口向下,对称轴为直线x=1,且与y轴的交点坐标为(0,2)的抛物线的解析式 .
14.已知二次函数 的图象如图所示,它与 轴的两个交点的坐标分别为(﹣1,0)(2,0).下列结论:① ;② ;③当 时, ;④当﹣1< <2时, <0.正确的有 .(填正确结论的序号).
15.已知抛物线 的对称轴是直线 ,其部分图象如图所示,下列说法中:① ;② ;③ ;④当 时, ,正确的是 (填写序号).
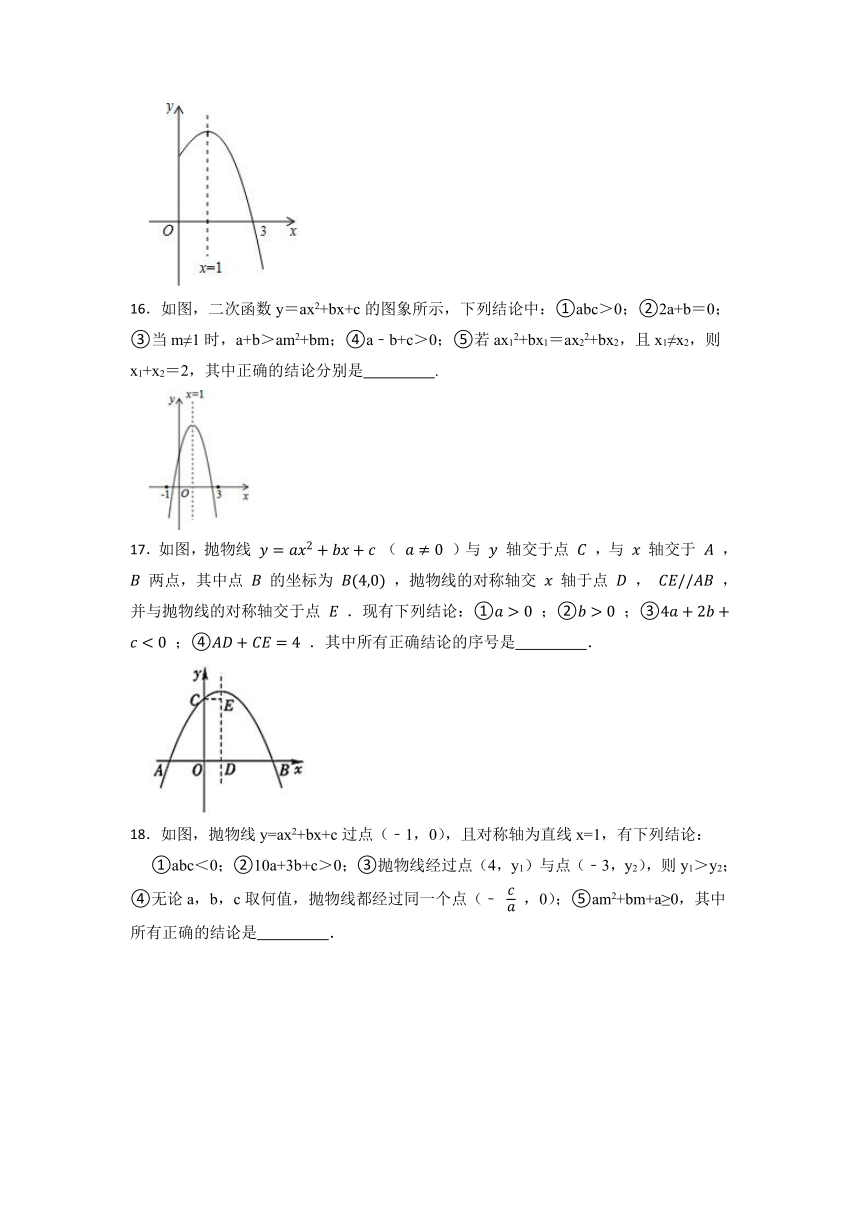
16.如图,二次函数y=ax2+bx+c的图象所示,下列结论中:①abc>0;②2a+b=0;③当m≠1时,a+b>am2+bm;④a﹣b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,则x1+x2=2,其中正确的结论分别是 .
17.如图,抛物线 ( )与 轴交于点 ,与 轴交于 , 两点,其中点 的坐标为 ,抛物线的对称轴交 轴于点 , ,并与抛物线的对称轴交于点 .现有下列结论:① ;② ;③ ;④ .其中所有正确结论的序号是 .
18.如图,抛物线y=ax2+bx+c过点(﹣1,0),且对称轴为直线x=1,有下列结论:
①abc<0;②10a+3b+c>0;③抛物线经过点(4,y1)与点(﹣3,y2),则y1>y2;④无论a,b,c取何值,抛物线都经过同一个点(﹣ ,0);⑤am2+bm+a≥0,其中所有正确的结论是 .
三、综合题(共6题;共70分)
19.在平面直角坐标系xOy中,二次函数y=mx2-(2m+1)x+m-5的图象与x轴有两个公共点.
(1)求m的取值范围;
(2)若m取满足条件的最小的整数,
①写出这个二次函数的表达式;
②当n≤x≤1时,函数值y的取值范围是-6≤y≤4-n,求n的值;
③将此二次函数图象平移,使平移后的图象经过原点O.设平移后的图象对应的函数表达式为y=a(x-h)2 +k,当x<2时,y随x的增大而减小,求k的取值范围.
20.已知抛物线y=ax2+bx+3的对称轴是直线x=1.
(1)求证:2a+b=0
(2)若关于x的方程ax2+bx﹣8=0的一个根为4,求方程的另一个根.
21.已知抛物线经过点(4,3),且当 时, 有最小值 .
(1)求这条抛物线的解析式.
(2)写出 随 的增大而减小的自变量 的取值范围.
22.已知二次函数y=﹣x2+6x﹣5的图象交x轴于A、B两点,点A在B左边,交y轴于点C.
(1)将函数y=﹣x2+6x﹣5的解析式化为y=a(x+m)2+k的形式,并指出该函数图象的开口方向、对称轴和顶点坐标;
(2)点D在该抛物线上,它是点C关于抛物线对称轴的对称点,求△ABD的面积.
23.如图,二次函数y=ax2+2x+c的图象与x轴交于点A(﹣1,0)和点B,与y轴交于点C(0,3).
(1)求该二次函数的表达式;
(2)过点A的直线AD∥BC且交抛物线于另一点D,求直线AD的函数表达式;
(3)在(2)的条件下,请解答下列问题:
①在x轴上是否存在一点P,使得以B、C、P为顶点的三角形与△ABD相似?若存在,求出点P的坐标;若不存在,请说明理由;
②动点M以每秒1个单位的速度沿线段AD从点A向点D运动,同时,动点N以每秒个单位的速度沿线段DB从点D向点B运动,问:在运动过程中,当运动时间t为何值时,△DMN的面积最大,并求出这个最大值.
24.已知:抛物线y=x2+(b﹣1)x﹣5.
(1)写出抛物线的开口方向和它与y轴交点的坐标;
(2)若抛物线的对称轴为直线x=1,求b的值,并画出抛物线的草图(不必列表);
(3)如图,若b>3,过抛物线上一点P(﹣1,c)作直线PA⊥y轴,垂足为A,交抛物线于另一点B,且BP=2PA,求这条抛物线所对应的二次函数解析式.
答案解析部分
1.【答案】B
2.【答案】D
3.【答案】B
4.【答案】B
5.【答案】D
6.【答案】C
7.【答案】A
8.【答案】C
9.【答案】D
10.【答案】C
11.【答案】C
12.【答案】C
13.【答案】y=﹣x2+2x+2
14.【答案】①②③
15.【答案】①③④
16.【答案】②③⑤
17.【答案】②④
18.【答案】②④⑤
19.【答案】解: ∵该二次函数图象与x轴有两个交点∴解:①②函数对称轴是直线x=1.5因为在n≤x≤1范围内,x=n时y取到最大值 而当n≤x≤1时,函数值y的取值范围是-6≤y≤4-n所以 得n=-2或n=4(不合题意)③由题意得a=1,图象经过原点,可得∵当x<2时,y随x的增大而减小 ∴则
(1)解:
∵该二次函数图象与x轴有两个交点
∴
(2)解:①
②函数对称轴是直线x=1.5
因为在n≤x≤1范围内,x=n时y取到最大值
而当n≤x≤1时,函数值y的取值范围是-6≤y≤4-n
所以
得n=-2或n=4(不合题意)
③由题意得a=1,图象经过原点,可得
∵当x<2时,y随x的增大而减小
∴则
20.【答案】(1)证明:∵对称轴是直线x=1=﹣,
∴2a+b=0;
(2)解:∵ax2+bx﹣8=0的一个根为4,
∴16a+4b﹣8=0,
∵2a+b=0,
∴b=﹣2a,
∴16a﹣8a﹣8=0,
解得:a=1,则b=﹣2,
∴ax2+bx﹣8=0为:x2﹣2x﹣8=0,
则(x﹣4)(x+2)=0,
解得:x1=4,x2=﹣2,
故方程的另一个根为:﹣2.
21.【答案】(1)解:设抛物线的解析式为:y=a(x-2)2-1,
把(4,3)代入,得4a-1=3,
∴a=1,
即y=(x-2)2-1 或y=x2-4x+3
(2)解:由y=(x-2)2-1知图形对称轴为x=2,且a=1>0,
∴ 随 的增大而减小的自变量 的取值范围是x<2.
22.【答案】(1)解:∵y=﹣x2+6x﹣5,,
∴该函数图象的开口向下,对称轴为,顶点坐标为;
(2)解:
由y=﹣x2+6x﹣5,令,
即,
解得,
,
,
令,则,
即,
点D在该抛物线上,它是点C关于抛物线对称轴的对称点,对称轴为,
,
.
23.【答案】(1)解:
由题意知:,
解得,
∴二次函数的表达式为y=﹣x2+2x+3
(2)解:
在y=﹣x2+2x+3中,令y=0,则﹣x2+2x+3=0,
解得:x1=﹣1,x2=3,
∴B(3,0),
由已知条件得直线BC的解析式为y=﹣x+3,
∵AD∥BC,
∴设直线AD的解析式为y=﹣x+b,
∴0=1+b,
∴b=﹣1,
∴直线AD的解析式为y=﹣x﹣1.
(3)解:①∵BC∥AD,∴∠DAB=∠CBA,∴只要当:或时,△PBC∽△ABD,解得D(4,﹣5),∴AD=,AB=4,BC=,设P的坐标为(x,0),
即或,
解得x=或x=﹣4.5,∴P(,0)或P(﹣4.5,0),②过点B作BF⊥AD于F,过点N作NE⊥AD于E,在Rt△AFB中,∠BAF=45°,∴sin∠BAF=,∴BF=,BD=,∴sin∠ADB=,∵DM=5-t,DN=t,
又∵sin∠ADB=,NE=,
∴∴当t=时,S△MDN的最大值为
24.【答案】(1)解:∵a=1>0,
∴抛物线开口向上,
当x=0时,y=02+(b﹣1)×0﹣5=﹣5,
∴它与y轴的交点坐标为(0,﹣5)
(2)解:抛物线的对称轴为x=1,
∴﹣ =﹣ =1,
解得b=﹣1,
故抛物线的解析式为y=x2﹣2x﹣5;
图象如下:
(3)解:∵b>3,
∴抛物线的对称轴x=﹣ =﹣ <﹣1,
∴对称轴在点P的左侧,
∵直线PA⊥y轴,且P(﹣1,c),BP=2PA,
∴点B的坐标为(﹣3,c),
把点B(﹣3,c)、P(﹣1,c)代入抛物线解析式y=x2+(b﹣1)x﹣5得,
,
解得 ,
∴抛物线所对应的二次函数解析式为y=x2+4x﹣5;
[或:∵点B(﹣3,c)、P(﹣1,c),
∴BP的中点(﹣2,c)在抛物线的对称轴上,
∴﹣ =﹣ =﹣2,解得b=5.]
一、单选题(共12题;共24分)
1.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;②b﹣a>c;③4a+2b+c>0;④3a>c;⑤a+b>m(am+b)(m≠1的实数),其中结论正确的有( )
A.①②③ B.②③⑤ C.②③④ D.③④⑤
2.在同一直角坐标系中,函数y=mx+m和y=﹣mx2+2x+2(m是常数,且m≠0)的图像可能是( )
A. B.
C. D.
3.函数与在同一直角坐标系中的大致图象可能是( )
A. B.
C. D.
4.如图是二次函数y=ax2+bx+c=(a≠0)图象的一部分,对称轴是直线x=﹣2.关于下列结论:①ab<0;②b2﹣4ac>0;③9a﹣3b+c<0;④b﹣4a=0;⑤方程ax2+bx=0的两个根为x1=0,x2=﹣4,其中正确的结论有( )
A.①③④ B.②④⑤ C.①②⑤ D.②③⑤
5.在同一平面直角坐标系中,函数y=ax+a和y=﹣ax2+a(a为常数,且a≠0)的图象可以是( )
A. B.
C. D.
6.对于二次函数y=2(x+1)(x﹣3),下列说法正确的是( )
A.图象的开口向下 B.当x>1时,y随x的增大而减小
C.当x<1时,y随x的增大而减小 D.图象的对称轴是直线x=﹣1
7.对于抛物线y=-(x-5)2+3,下列说法正确的是 ( )
A.开口向下,顶点坐标(5,3)
B.开口向上,顶点坐标(5,3)
C.开口向下,顶点坐标(-5,3)
D.开口向上,顶点坐标(-5,3)
8.小明从二次函数y=ax2+bx+c的图象(如图)中观察得出了下面五条信息:①c<0;②abc>0;③a-b+c>0;④2a-3b=0.你认为其中正确的信息的个数是( )
A.1 B.2 C.3 D.4
9.已知二次函数y=ax2+bx+c(a,b,c是常数,且a≠0)的图象如图所示,则一次函数y=cx+ 与反比例函数 在同一坐标系内的大致图象是( )
A. B.
C. D.
10.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是x=1,下列结论:①abc<0;②b2>4ac;③a+b+c<0;④3a+c>0,其中正确结论的个数为( )
A.1个 B.2个 C.3个 D.4个
11.如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴正半轴相交于A、B两点,与y轴相交于点C,对称轴为直线x=2,且OA=OC,则下列结论:①abc>0;②9a+3b+c<0;③c>﹣1;④关于x的方程ax2+bx+c=0(a≠0)有一个根为,其中正确结论的个数为( )
A.1 B.2 C.3 D.4
12.已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:①a+b+c<0;②a-b+c>1;③ab>0;④4a-2b+c<0;⑤c-a>1.其中所有正确的个数是( )
A.2 B.3 C.4 D.5
二、填空题(共6题;共6分)
13.请写出一个开口向下,对称轴为直线x=1,且与y轴的交点坐标为(0,2)的抛物线的解析式 .
14.已知二次函数 的图象如图所示,它与 轴的两个交点的坐标分别为(﹣1,0)(2,0).下列结论:① ;② ;③当 时, ;④当﹣1< <2时, <0.正确的有 .(填正确结论的序号).
15.已知抛物线 的对称轴是直线 ,其部分图象如图所示,下列说法中:① ;② ;③ ;④当 时, ,正确的是 (填写序号).
16.如图,二次函数y=ax2+bx+c的图象所示,下列结论中:①abc>0;②2a+b=0;③当m≠1时,a+b>am2+bm;④a﹣b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,则x1+x2=2,其中正确的结论分别是 .
17.如图,抛物线 ( )与 轴交于点 ,与 轴交于 , 两点,其中点 的坐标为 ,抛物线的对称轴交 轴于点 , ,并与抛物线的对称轴交于点 .现有下列结论:① ;② ;③ ;④ .其中所有正确结论的序号是 .
18.如图,抛物线y=ax2+bx+c过点(﹣1,0),且对称轴为直线x=1,有下列结论:
①abc<0;②10a+3b+c>0;③抛物线经过点(4,y1)与点(﹣3,y2),则y1>y2;④无论a,b,c取何值,抛物线都经过同一个点(﹣ ,0);⑤am2+bm+a≥0,其中所有正确的结论是 .
三、综合题(共6题;共70分)
19.在平面直角坐标系xOy中,二次函数y=mx2-(2m+1)x+m-5的图象与x轴有两个公共点.
(1)求m的取值范围;
(2)若m取满足条件的最小的整数,
①写出这个二次函数的表达式;
②当n≤x≤1时,函数值y的取值范围是-6≤y≤4-n,求n的值;
③将此二次函数图象平移,使平移后的图象经过原点O.设平移后的图象对应的函数表达式为y=a(x-h)2 +k,当x<2时,y随x的增大而减小,求k的取值范围.
20.已知抛物线y=ax2+bx+3的对称轴是直线x=1.
(1)求证:2a+b=0
(2)若关于x的方程ax2+bx﹣8=0的一个根为4,求方程的另一个根.
21.已知抛物线经过点(4,3),且当 时, 有最小值 .
(1)求这条抛物线的解析式.
(2)写出 随 的增大而减小的自变量 的取值范围.
22.已知二次函数y=﹣x2+6x﹣5的图象交x轴于A、B两点,点A在B左边,交y轴于点C.
(1)将函数y=﹣x2+6x﹣5的解析式化为y=a(x+m)2+k的形式,并指出该函数图象的开口方向、对称轴和顶点坐标;
(2)点D在该抛物线上,它是点C关于抛物线对称轴的对称点,求△ABD的面积.
23.如图,二次函数y=ax2+2x+c的图象与x轴交于点A(﹣1,0)和点B,与y轴交于点C(0,3).
(1)求该二次函数的表达式;
(2)过点A的直线AD∥BC且交抛物线于另一点D,求直线AD的函数表达式;
(3)在(2)的条件下,请解答下列问题:
①在x轴上是否存在一点P,使得以B、C、P为顶点的三角形与△ABD相似?若存在,求出点P的坐标;若不存在,请说明理由;
②动点M以每秒1个单位的速度沿线段AD从点A向点D运动,同时,动点N以每秒个单位的速度沿线段DB从点D向点B运动,问:在运动过程中,当运动时间t为何值时,△DMN的面积最大,并求出这个最大值.
24.已知:抛物线y=x2+(b﹣1)x﹣5.
(1)写出抛物线的开口方向和它与y轴交点的坐标;
(2)若抛物线的对称轴为直线x=1,求b的值,并画出抛物线的草图(不必列表);
(3)如图,若b>3,过抛物线上一点P(﹣1,c)作直线PA⊥y轴,垂足为A,交抛物线于另一点B,且BP=2PA,求这条抛物线所对应的二次函数解析式.
答案解析部分
1.【答案】B
2.【答案】D
3.【答案】B
4.【答案】B
5.【答案】D
6.【答案】C
7.【答案】A
8.【答案】C
9.【答案】D
10.【答案】C
11.【答案】C
12.【答案】C
13.【答案】y=﹣x2+2x+2
14.【答案】①②③
15.【答案】①③④
16.【答案】②③⑤
17.【答案】②④
18.【答案】②④⑤
19.【答案】解: ∵该二次函数图象与x轴有两个交点∴解:①②函数对称轴是直线x=1.5因为在n≤x≤1范围内,x=n时y取到最大值 而当n≤x≤1时,函数值y的取值范围是-6≤y≤4-n所以 得n=-2或n=4(不合题意)③由题意得a=1,图象经过原点,可得∵当x<2时,y随x的增大而减小 ∴则
(1)解:
∵该二次函数图象与x轴有两个交点
∴
(2)解:①
②函数对称轴是直线x=1.5
因为在n≤x≤1范围内,x=n时y取到最大值
而当n≤x≤1时,函数值y的取值范围是-6≤y≤4-n
所以
得n=-2或n=4(不合题意)
③由题意得a=1,图象经过原点,可得
∵当x<2时,y随x的增大而减小
∴则
20.【答案】(1)证明:∵对称轴是直线x=1=﹣,
∴2a+b=0;
(2)解:∵ax2+bx﹣8=0的一个根为4,
∴16a+4b﹣8=0,
∵2a+b=0,
∴b=﹣2a,
∴16a﹣8a﹣8=0,
解得:a=1,则b=﹣2,
∴ax2+bx﹣8=0为:x2﹣2x﹣8=0,
则(x﹣4)(x+2)=0,
解得:x1=4,x2=﹣2,
故方程的另一个根为:﹣2.
21.【答案】(1)解:设抛物线的解析式为:y=a(x-2)2-1,
把(4,3)代入,得4a-1=3,
∴a=1,
即y=(x-2)2-1 或y=x2-4x+3
(2)解:由y=(x-2)2-1知图形对称轴为x=2,且a=1>0,
∴ 随 的增大而减小的自变量 的取值范围是x<2.
22.【答案】(1)解:∵y=﹣x2+6x﹣5,,
∴该函数图象的开口向下,对称轴为,顶点坐标为;
(2)解:
由y=﹣x2+6x﹣5,令,
即,
解得,
,
,
令,则,
即,
点D在该抛物线上,它是点C关于抛物线对称轴的对称点,对称轴为,
,
.
23.【答案】(1)解:
由题意知:,
解得,
∴二次函数的表达式为y=﹣x2+2x+3
(2)解:
在y=﹣x2+2x+3中,令y=0,则﹣x2+2x+3=0,
解得:x1=﹣1,x2=3,
∴B(3,0),
由已知条件得直线BC的解析式为y=﹣x+3,
∵AD∥BC,
∴设直线AD的解析式为y=﹣x+b,
∴0=1+b,
∴b=﹣1,
∴直线AD的解析式为y=﹣x﹣1.
(3)解:①∵BC∥AD,∴∠DAB=∠CBA,∴只要当:或时,△PBC∽△ABD,解得D(4,﹣5),∴AD=,AB=4,BC=,设P的坐标为(x,0),
即或,
解得x=或x=﹣4.5,∴P(,0)或P(﹣4.5,0),②过点B作BF⊥AD于F,过点N作NE⊥AD于E,在Rt△AFB中,∠BAF=45°,∴sin∠BAF=,∴BF=,BD=,∴sin∠ADB=,∵DM=5-t,DN=t,
又∵sin∠ADB=,NE=,
∴∴当t=时,S△MDN的最大值为
24.【答案】(1)解:∵a=1>0,
∴抛物线开口向上,
当x=0时,y=02+(b﹣1)×0﹣5=﹣5,
∴它与y轴的交点坐标为(0,﹣5)
(2)解:抛物线的对称轴为x=1,
∴﹣ =﹣ =1,
解得b=﹣1,
故抛物线的解析式为y=x2﹣2x﹣5;
图象如下:
(3)解:∵b>3,
∴抛物线的对称轴x=﹣ =﹣ <﹣1,
∴对称轴在点P的左侧,
∵直线PA⊥y轴,且P(﹣1,c),BP=2PA,
∴点B的坐标为(﹣3,c),
把点B(﹣3,c)、P(﹣1,c)代入抛物线解析式y=x2+(b﹣1)x﹣5得,
,
解得 ,
∴抛物线所对应的二次函数解析式为y=x2+4x﹣5;
[或:∵点B(﹣3,c)、P(﹣1,c),
∴BP的中点(﹣2,c)在抛物线的对称轴上,
∴﹣ =﹣ =﹣2,解得b=5.]
同课章节目录
