人教版五年级下册 数学分数的再认识 教案
文档属性
| 名称 | 人教版五年级下册 数学分数的再认识 教案 |  | |
| 格式 | docx | ||
| 文件大小 | 180.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-12 20:32:18 | ||
图片预览



文档简介
分数的再认识
教学目标
1:结合具体情境,经历独立画图表示出分数,概括分数意义的过程,理解分数表示多少的相对性;在具体情境中发展数感,体会分数与生活的密切联系。
2:结合具体情境,经历独立画图表示出分数的过程,通过小组交流,经历概括分数意义,理解分数表示多少的相对性;在具体情境中感知分数与生活的密切联系,发展数感。
3:结合具体情境,经历独立画图表示出分数的过程,通过小组交流帮扶,经历概括分数意义,理解分数表示多少的相对性;在具体情境中感知分数与生活的密切联系,发展数感。
教学重点:理解分数的意义,理解分数表示多少的相对性
教学难点:理解分数表示多少的相对性
课前谈话:
同学们好。
同学们,认识他吗?这就是我国伟大的数学家华罗庚爷爷,他曾经说过:数源于数
这句话怎么理解?(生:数是数出来的)你说得很对,同时我要为第一个大胆发言的你点赞。
数数看(出手指),1个1是1,2 个1是2……
比如我们班有多少个同学?31就是这样1个1个地数出来的。
当然还可以这样数数:1个十是十……
整数可以这样数,那小数呢?(生:)你到来数数看。还可以0.01,0.01地数,
的确,通过计数单位的累加,可以帮助我们认识许许多多的整数和小数。
分数是不是也能这样数呢?
让我们一起进入今天的数学课堂。
教学过程:
导入
1、自主表征
师:出示,这个分数,你打算怎么填?
四分之一、四分之二、四分之三、四分之四、四分之五、四分之六……
填的完吗?
这么多的分数,你知道他们所表示的意义吗?
选个简单的,四分之五吧,用自己喜欢的方式表示的意义,完成后同桌交流。练习纸的第一题,开始吧。
2、反馈交流
三图一屏,分别是没有平均分、平均分成5分、正确的
你认为那幅图可以表示四分之五?
反馈1:(生1:不对,没有平均分。)
师:有道理,分数的前提是平均分。(手点黑板)
反馈2:(生:四分之五要平均分成4份,这里平均分成了5份,不对)
师:分母是4,就要平均分成4份。
反馈3:正确答案,怎么理解?
把一个圆看作单位“1”,平均分成4份,表示这样的5份,用四分之五表示
大家听懂了吗?有什么问题?我可以提个问题吗?
我觉得这是平均分成8份,取了其中的5份,不是八分之五吗?
(生:八分之五是把2个圆看作单位“1”,我们这里是把一个圆看作单位“1”,平均分成4份,表示这样的5份)
谁听懂了他的意思
你们的意思是四分之五以1个圆为单位“1”的,而8分之五却是以两个圆为单位“1”的。看来,规定单位“1”很重要。(练习纸上标“1”,和大括号。)
现在谁来说一说,到底四分之五表示什么意义
把一个圆看作单位“1”,平均分成4分,表示这样的5份,用四分之五表示。
谁能像我这样说?2人说
长方形。
线段。
小结板书:把一个圆看作单位“1”,平均分成4份,这样的5份就是。
同桌之间互相说一说。
看来,当一个单位“1”不够时,需要多个单位“1”一起帮忙。
四分之五的分数单位是多少?有几个分数单位呢?
我们一起数一数。
课件演示逐一累加的过程,数一数。
那么,又该怎么表示呢?
生:要再增加一个单位1
把一个圆看作单位“1”,平均分成4份,这样的9份就是,有9个。
我们一起数一数,验证一下。
小步子练习丰富分数
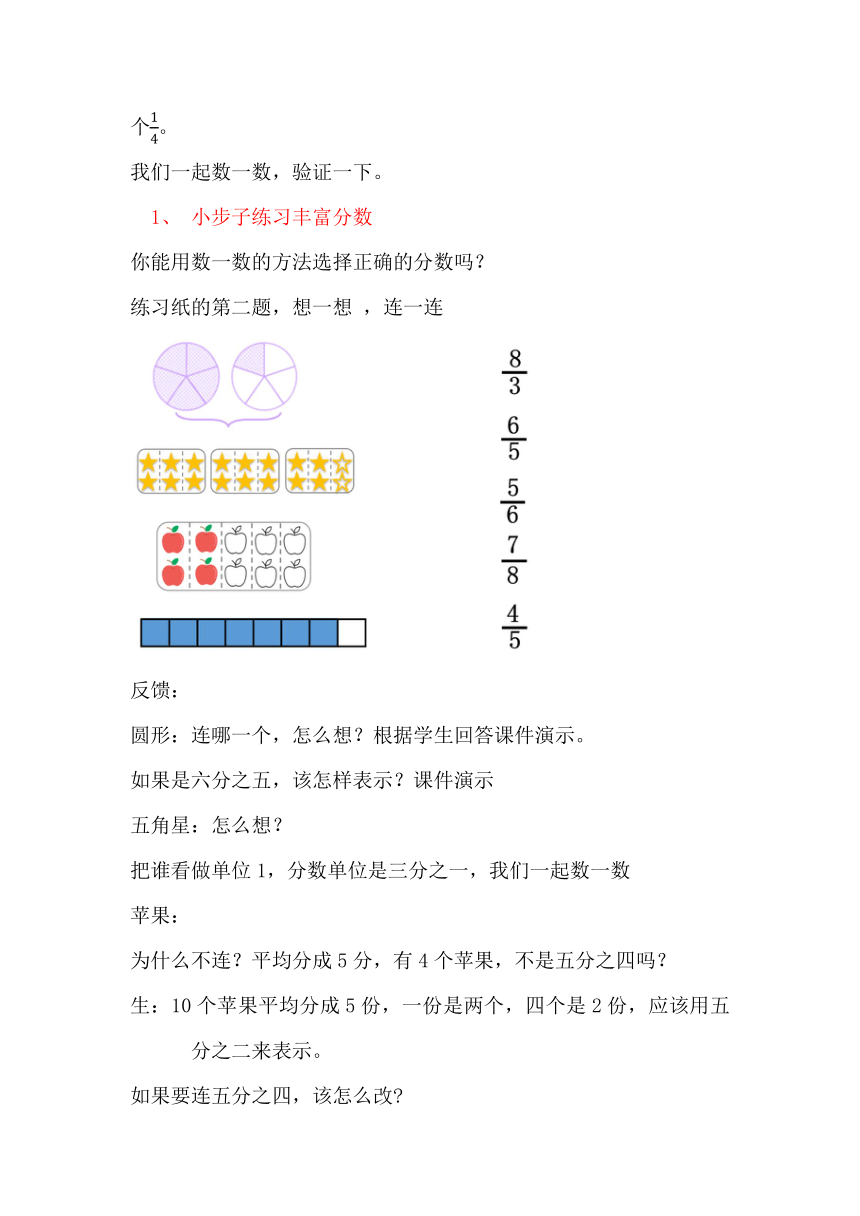
你能用数一数的方法选择正确的分数吗?
练习纸的第二题,想一想 ,连一连
反馈:
圆形:连哪一个,怎么想?根据学生回答课件演示。
如果是六分之五,该怎样表示?课件演示
五角星:怎么想?
把谁看做单位1,分数单位是三分之一,我们一起数一数
苹果:
为什么不连?平均分成5分,有4个苹果,不是五分之四吗?
生:10个苹果平均分成5份,一份是两个,四个是2份,应该用五分之二来表示。
如果要连五分之四,该怎么改
再涂两份
课件修改,连线
正方形:直接连
还是这8个小正方形,变一变,该用哪个分数来表示?四分之七
再变,二分之七
为什么都是8个小正方形,涂了7个,一会儿八分之七,一会儿四分
之七,一会儿二分之七?
生:单位“1”不同
看来把谁看做单位“1”很重要
5、真分数和假分数
(1)数轴上表示分数(图和数轴结合)
师:同学们,刚才我们是用一些图形和物体来表示分数,你能在直线上表示吗?
四分之一
生:把单位“1”平均分成4份,0后面的第一小格是(课件出示)那在哪儿?哦,一个单位“1”不够了,2个是?接着就是……,还能数出无数个这样四分之几的分数。
师:黑板上剩下的这些分数在什么位置呢?
在谁和谁之间??为什么?那么在哪里?在大概在哪里?
(2)真分数和假分数
①观察发现,出示名称
师:仔细观察直线上的分数,你有什么发现?四人小组讨论,看哪个组的发现最多?
(先叫学生分子和分母的大小的)
反馈1:(生:有些分数的分子比分母小,有些分数的分子比分母大,)
师:好,你们关注了分子分母比大小,那这一类分数就孤单了。(生:还有分子等于分母的)
师:是的,根据分子分母的大小,我们可以把分数分成真分数和假分数,(课件)
师:谁来说说,什么是真分数,什么是假分数?
(生:分子比分母小的分数是真分数,分子大于或等于分母的分数是假分数。)
同学们很会观察,还有发现吗?
反馈2:生:分子等于分母的分数都等于1。
师:这样等于的1的分数你还能举几个例子吗?
反馈3:师:关注了1,来想想2,想想3,这些点上表示的分数会有什么特点呢?
生:分子师分母的2倍,都可以表示在2这个点上。、、、
师:分子是分母的倍数时,都等于一个整数。
反馈4:你认为除了这里出示的分数,真分数假分数还有吗?会有多少个?
生:真分数和假分数的个数是无限的。
师:真的吗?就这么一段,能表示出无限个真分数?
那我来考考大家:
师: 如果分子分母是整数,分母是5的真分数有哪些?分母是5的最大真分数是?
师:可能是什么分数?(生:)
如果分子分母是整数,是假分数,x最大是几?是真分数,x最小是几?
6、跑点A
如果所有的分数都隐去,只剩下一个A点,你能快速判断它是真分数还是假分数吗?口答,看谁反应快。
为什么你能这么快速地判断?
因为真分数<1,假分数≥1
完善板书。
师:这里有4个分数,请看(出示a\b\c\d\e)中哪个是、?
你怎么思考的?那么C和D比哪个大?其实,假分数还真有另一种与整数有关的写法呢?这是我们下节课要研究的内容。
师:为什么不选B呢?因为分子分母相等,虽然是假分数,但不符合要求。你为什么不选 a呢? 谁会填?(A\和C相比)?谁会填?(A\和D相比)?说明什么?真验证了你们的结论真分数小于假分数。
辩一辩:
10杯果汁,平均分给9人,每人分得杯果汁。
算式怎么列?
10÷9=。
10杯果汁的,就是一杯果汁的,能从分数与除法的角度研究,非常好。
反馈三:
女生人数是男生人数的。
谁是单位“1”?这句话表示的意思是把男生人数平均分成9份,9人就是单位“1”的,女生10人就是单位“1”的。
原来通过男生和女生两个量的对比,也能理解的意义。
整合:其实,研究到这儿,我们发现,不论是哪种方法,都是先把单位“1”平均分成9份,这样的10份,就是。
课堂小结、延伸概念
通过本节课的学习,你对分数有了哪些新的认识?
教学目标
1:结合具体情境,经历独立画图表示出分数,概括分数意义的过程,理解分数表示多少的相对性;在具体情境中发展数感,体会分数与生活的密切联系。
2:结合具体情境,经历独立画图表示出分数的过程,通过小组交流,经历概括分数意义,理解分数表示多少的相对性;在具体情境中感知分数与生活的密切联系,发展数感。
3:结合具体情境,经历独立画图表示出分数的过程,通过小组交流帮扶,经历概括分数意义,理解分数表示多少的相对性;在具体情境中感知分数与生活的密切联系,发展数感。
教学重点:理解分数的意义,理解分数表示多少的相对性
教学难点:理解分数表示多少的相对性
课前谈话:
同学们好。
同学们,认识他吗?这就是我国伟大的数学家华罗庚爷爷,他曾经说过:数源于数
这句话怎么理解?(生:数是数出来的)你说得很对,同时我要为第一个大胆发言的你点赞。
数数看(出手指),1个1是1,2 个1是2……
比如我们班有多少个同学?31就是这样1个1个地数出来的。
当然还可以这样数数:1个十是十……
整数可以这样数,那小数呢?(生:)你到来数数看。还可以0.01,0.01地数,
的确,通过计数单位的累加,可以帮助我们认识许许多多的整数和小数。
分数是不是也能这样数呢?
让我们一起进入今天的数学课堂。
教学过程:
导入
1、自主表征
师:出示,这个分数,你打算怎么填?
四分之一、四分之二、四分之三、四分之四、四分之五、四分之六……
填的完吗?
这么多的分数,你知道他们所表示的意义吗?
选个简单的,四分之五吧,用自己喜欢的方式表示的意义,完成后同桌交流。练习纸的第一题,开始吧。
2、反馈交流
三图一屏,分别是没有平均分、平均分成5分、正确的
你认为那幅图可以表示四分之五?
反馈1:(生1:不对,没有平均分。)
师:有道理,分数的前提是平均分。(手点黑板)
反馈2:(生:四分之五要平均分成4份,这里平均分成了5份,不对)
师:分母是4,就要平均分成4份。
反馈3:正确答案,怎么理解?
把一个圆看作单位“1”,平均分成4份,表示这样的5份,用四分之五表示
大家听懂了吗?有什么问题?我可以提个问题吗?
我觉得这是平均分成8份,取了其中的5份,不是八分之五吗?
(生:八分之五是把2个圆看作单位“1”,我们这里是把一个圆看作单位“1”,平均分成4份,表示这样的5份)
谁听懂了他的意思
你们的意思是四分之五以1个圆为单位“1”的,而8分之五却是以两个圆为单位“1”的。看来,规定单位“1”很重要。(练习纸上标“1”,和大括号。)
现在谁来说一说,到底四分之五表示什么意义
把一个圆看作单位“1”,平均分成4分,表示这样的5份,用四分之五表示。
谁能像我这样说?2人说
长方形。
线段。
小结板书:把一个圆看作单位“1”,平均分成4份,这样的5份就是。
同桌之间互相说一说。
看来,当一个单位“1”不够时,需要多个单位“1”一起帮忙。
四分之五的分数单位是多少?有几个分数单位呢?
我们一起数一数。
课件演示逐一累加的过程,数一数。
那么,又该怎么表示呢?
生:要再增加一个单位1
把一个圆看作单位“1”,平均分成4份,这样的9份就是,有9个。
我们一起数一数,验证一下。
小步子练习丰富分数
你能用数一数的方法选择正确的分数吗?
练习纸的第二题,想一想 ,连一连
反馈:
圆形:连哪一个,怎么想?根据学生回答课件演示。
如果是六分之五,该怎样表示?课件演示
五角星:怎么想?
把谁看做单位1,分数单位是三分之一,我们一起数一数
苹果:
为什么不连?平均分成5分,有4个苹果,不是五分之四吗?
生:10个苹果平均分成5份,一份是两个,四个是2份,应该用五分之二来表示。
如果要连五分之四,该怎么改
再涂两份
课件修改,连线
正方形:直接连
还是这8个小正方形,变一变,该用哪个分数来表示?四分之七
再变,二分之七
为什么都是8个小正方形,涂了7个,一会儿八分之七,一会儿四分
之七,一会儿二分之七?
生:单位“1”不同
看来把谁看做单位“1”很重要
5、真分数和假分数
(1)数轴上表示分数(图和数轴结合)
师:同学们,刚才我们是用一些图形和物体来表示分数,你能在直线上表示吗?
四分之一
生:把单位“1”平均分成4份,0后面的第一小格是(课件出示)那在哪儿?哦,一个单位“1”不够了,2个是?接着就是……,还能数出无数个这样四分之几的分数。
师:黑板上剩下的这些分数在什么位置呢?
在谁和谁之间??为什么?那么在哪里?在大概在哪里?
(2)真分数和假分数
①观察发现,出示名称
师:仔细观察直线上的分数,你有什么发现?四人小组讨论,看哪个组的发现最多?
(先叫学生分子和分母的大小的)
反馈1:(生:有些分数的分子比分母小,有些分数的分子比分母大,)
师:好,你们关注了分子分母比大小,那这一类分数就孤单了。(生:还有分子等于分母的)
师:是的,根据分子分母的大小,我们可以把分数分成真分数和假分数,(课件)
师:谁来说说,什么是真分数,什么是假分数?
(生:分子比分母小的分数是真分数,分子大于或等于分母的分数是假分数。)
同学们很会观察,还有发现吗?
反馈2:生:分子等于分母的分数都等于1。
师:这样等于的1的分数你还能举几个例子吗?
反馈3:师:关注了1,来想想2,想想3,这些点上表示的分数会有什么特点呢?
生:分子师分母的2倍,都可以表示在2这个点上。、、、
师:分子是分母的倍数时,都等于一个整数。
反馈4:你认为除了这里出示的分数,真分数假分数还有吗?会有多少个?
生:真分数和假分数的个数是无限的。
师:真的吗?就这么一段,能表示出无限个真分数?
那我来考考大家:
师: 如果分子分母是整数,分母是5的真分数有哪些?分母是5的最大真分数是?
师:可能是什么分数?(生:)
如果分子分母是整数,是假分数,x最大是几?是真分数,x最小是几?
6、跑点A
如果所有的分数都隐去,只剩下一个A点,你能快速判断它是真分数还是假分数吗?口答,看谁反应快。
为什么你能这么快速地判断?
因为真分数<1,假分数≥1
完善板书。
师:这里有4个分数,请看(出示a\b\c\d\e)中哪个是、?
你怎么思考的?那么C和D比哪个大?其实,假分数还真有另一种与整数有关的写法呢?这是我们下节课要研究的内容。
师:为什么不选B呢?因为分子分母相等,虽然是假分数,但不符合要求。你为什么不选 a呢? 谁会填?(A\和C相比)?谁会填?(A\和D相比)?说明什么?真验证了你们的结论真分数小于假分数。
辩一辩:
10杯果汁,平均分给9人,每人分得杯果汁。
算式怎么列?
10÷9=。
10杯果汁的,就是一杯果汁的,能从分数与除法的角度研究,非常好。
反馈三:
女生人数是男生人数的。
谁是单位“1”?这句话表示的意思是把男生人数平均分成9份,9人就是单位“1”的,女生10人就是单位“1”的。
原来通过男生和女生两个量的对比,也能理解的意义。
整合:其实,研究到这儿,我们发现,不论是哪种方法,都是先把单位“1”平均分成9份,这样的10份,就是。
课堂小结、延伸概念
通过本节课的学习,你对分数有了哪些新的认识?
