同底数幂的乘法[上学期]
图片预览

文档简介
同底数幂的乘法
执教人:曹劲松
一、教学目标:
1.知识与技能:理解掌握同底数幂乘法的运算性质,并能够熟练运用性质进行计算.
2.过程与方法:通过推导运算性质,培养学生观察、概括与抽象的能力。
3.情感、态度与价值观:通过学生自己发现问题,培养他们解决问题的能力,激发学生勇往直前的斗志,进而培养他们积极的学习态度.
二、学法引导
1.教学方法:尝试指导法、探究法.
2.学生学法:运用归纳法由特殊性推导出公式所具有的一般性,在探究规律过程中渐增对知识的理解.
三、重点:幂的运算性质.
难点:有关字母的广泛含义及“性质”的正确使用.
四、教学过程设计
问题与情境 师生行为 设计意图
创设情境,复习导入
问题:一种电子计算机每秒可进行1012次运算,它工作103秒可进行多少次运算?上面问题中这个积中的两个因式有何特点?式子1012×103的意义是什么? 分析得出算式:1012×103学生回答:底数相同。同底数幂的乘法。 由现实中的实际问题入手,设置情景问题,激发学生的学习兴趣。
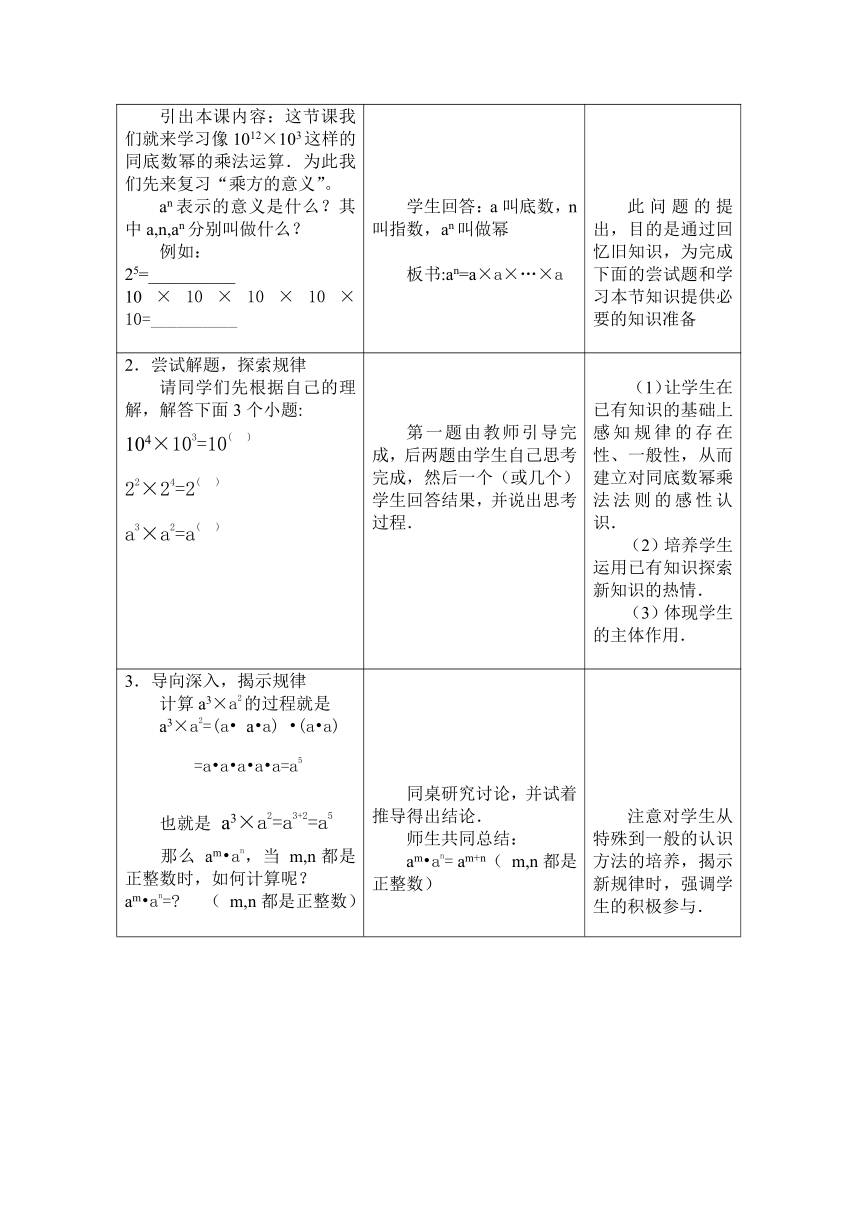
引出本课内容:这节课我们就来学习像1012×103这样的同底数幂的乘法运算.为此我们先来复习“乘方的意义”。an表示的意义是什么?其中a,n,an分别叫做什么?例如:25=__________10×10×10×10×10=__________ 学生回答:a叫底数,n叫指数,an叫做幂板书:an=a×a×…×a 此问题的提出,目的是通过回忆旧知识,为完成下面的尝试题和学习本节知识提供必要的知识准备
2.尝试解题,探索规律请同学们先根据自己的理解,解答下面3个小题:104×103=10( )22×24=2( )a3×a2=a( ) 第一题由教师引导完成,后两题由学生自己思考完成,然后一个(或几个)学生回答结果,并说出思考过程. (1)让学生在已有知识的基础上感知规律的存在性、一般性,从而建立对同底数幂乘法法则的感性认识. (2)培养学生运用已有知识探索新知识的热情. (3)体现学生的主体作用.
3.导向深入,揭示规律计算a3×a2的过程就是a3×a2=(a a a) (a a)=a a a a a=a5也就是 a3×a2=a3+2=a5 那么 am an,当 m,n都是正整数时,如何计算呢?am an= ( m,n都是正整数) 同桌研究讨论,并试着推导得出结论.师生共同总结:am an= am+n( m,n都是正整数) 注意对学生从特殊到一般的认识方法的培养,揭示新规律时,强调学生的积极参与.
引导学生剖析法则:①等号左边是什么运算?②等号两边的底数有什么关系?③等号两边的指数有什么关系? ④公式中的底数a可以表示什么? ⑤当三个或三个以上同底数幂相乘时,是否也具有这一性质呢?现在你能轻松地算出问题中出现的1012×103吗? 学生活动:观察am an ap=am+n+p ( m,n,p都是正整数)请同学们试着用文字概括这个性质:同底数幂相乘底数不变、指数相加运算形式 运算方法师生共同完成
4.尝试反馈,理解新知例1 计算:107 ×104 x2 x5xm x3m+1例2 计算:2×24×23 y y2 y3 学生在练习本上完成例1、例2,由2个学生板演完成之后,由学生判断板演是否正确.教师统计做题正确的人数,同时给予肯定或鼓励.注意问题:例2中第一个 的指数都是1,这是学生做题时易出问题之处. 学生在认识的基础上,尝试运用性质,加深对性质的理解.学生做题正确与否,教师均应以鼓励为主,增强学生学习的信心.
5.反馈练习,巩固知识 练习一 (1)计算: ①105×106②a7 a3 ③ b5 b ④a6 a6(2)计算: ①x10 x ②10×102×10 第(1)题由学生口答;第(2)题在练习本上完成,然后同桌互阅,教师抽查. 练习一主要是对性质运用的强化,形成定势.
③y4 y3 y2 y④–a2 a6练习二下面的计算对不对?如果不对,应怎样改正?(1)b5 b5=2b5(2)b5+b5=b10 (3)x5 x5=2x10 (4)x5x5=x25 (5)c c3=c3 (6)m+m3=m4 此练习以学生抢答方式完成.注意训练学生的表述能力,以提高兴趣. 练习二中主要是通过学生对题目的观察、比较、判断,提高学生的是非辨别能力.(1)(2)小题强调同底数幂乘法与整式加减的区别.(3)(4)小题强调性质中的“不变”、“相加”.(5)小题强调“c ”表示“c ”的一次幂.
6.变式训练,培养能力 练习三 填空: (1)x5 ( )=x8 (2)a ( )=a6 (3)x x3 ( )=x7(4)xm ( )=x3m(5)xα ( )=xα+β练习四填空:(1)8=2x ,则x=_____ .(2)8×4=2x ,则x= ______ .(3)3×27×9=3x,则x=_____ . 学生思考后回答.学生同桌或前后左右结组研究、讨论,然后完成. 这组题的目的是训练学生的逆向思维能力.此组题旨在增强学生应变能力和解题灵活性.
7.总结、扩展同底数幂相乘,底数____________,指数____________. 由学生说出本节体会最深的是哪些? 在性质中强调“不变”、“相加”.学生谈体会,不仅是对本节知识的再现,同时也培养了学生的口头表达能力和概括总结能力.
8.布置作业1.计算:(必做题)(1)a3·a4; (2)x3·x; (3) 105· 10· 103;(4) x7· x· x12.2.计算:(选做题)(1)x·x3 +x2·x2; (2)y3·y-y·y·y2;(3) 32· 3· 9-3· 34; (4) 103· 10+100· 102.3.思考与拓展:(1)(–x) ·(–x)3 (2)–b·(–b)2 ·b2(3)an - 1 ·(–a)2 (4)(x+2y)2·(2y+x)3
五、教学反思:
执教人:曹劲松
一、教学目标:
1.知识与技能:理解掌握同底数幂乘法的运算性质,并能够熟练运用性质进行计算.
2.过程与方法:通过推导运算性质,培养学生观察、概括与抽象的能力。
3.情感、态度与价值观:通过学生自己发现问题,培养他们解决问题的能力,激发学生勇往直前的斗志,进而培养他们积极的学习态度.
二、学法引导
1.教学方法:尝试指导法、探究法.
2.学生学法:运用归纳法由特殊性推导出公式所具有的一般性,在探究规律过程中渐增对知识的理解.
三、重点:幂的运算性质.
难点:有关字母的广泛含义及“性质”的正确使用.
四、教学过程设计
问题与情境 师生行为 设计意图
创设情境,复习导入
问题:一种电子计算机每秒可进行1012次运算,它工作103秒可进行多少次运算?上面问题中这个积中的两个因式有何特点?式子1012×103的意义是什么? 分析得出算式:1012×103学生回答:底数相同。同底数幂的乘法。 由现实中的实际问题入手,设置情景问题,激发学生的学习兴趣。
引出本课内容:这节课我们就来学习像1012×103这样的同底数幂的乘法运算.为此我们先来复习“乘方的意义”。an表示的意义是什么?其中a,n,an分别叫做什么?例如:25=__________10×10×10×10×10=__________ 学生回答:a叫底数,n叫指数,an叫做幂板书:an=a×a×…×a 此问题的提出,目的是通过回忆旧知识,为完成下面的尝试题和学习本节知识提供必要的知识准备
2.尝试解题,探索规律请同学们先根据自己的理解,解答下面3个小题:104×103=10( )22×24=2( )a3×a2=a( ) 第一题由教师引导完成,后两题由学生自己思考完成,然后一个(或几个)学生回答结果,并说出思考过程. (1)让学生在已有知识的基础上感知规律的存在性、一般性,从而建立对同底数幂乘法法则的感性认识. (2)培养学生运用已有知识探索新知识的热情. (3)体现学生的主体作用.
3.导向深入,揭示规律计算a3×a2的过程就是a3×a2=(a a a) (a a)=a a a a a=a5也就是 a3×a2=a3+2=a5 那么 am an,当 m,n都是正整数时,如何计算呢?am an= ( m,n都是正整数) 同桌研究讨论,并试着推导得出结论.师生共同总结:am an= am+n( m,n都是正整数) 注意对学生从特殊到一般的认识方法的培养,揭示新规律时,强调学生的积极参与.
引导学生剖析法则:①等号左边是什么运算?②等号两边的底数有什么关系?③等号两边的指数有什么关系? ④公式中的底数a可以表示什么? ⑤当三个或三个以上同底数幂相乘时,是否也具有这一性质呢?现在你能轻松地算出问题中出现的1012×103吗? 学生活动:观察am an ap=am+n+p ( m,n,p都是正整数)请同学们试着用文字概括这个性质:同底数幂相乘底数不变、指数相加运算形式 运算方法师生共同完成
4.尝试反馈,理解新知例1 计算:107 ×104 x2 x5xm x3m+1例2 计算:2×24×23 y y2 y3 学生在练习本上完成例1、例2,由2个学生板演完成之后,由学生判断板演是否正确.教师统计做题正确的人数,同时给予肯定或鼓励.注意问题:例2中第一个 的指数都是1,这是学生做题时易出问题之处. 学生在认识的基础上,尝试运用性质,加深对性质的理解.学生做题正确与否,教师均应以鼓励为主,增强学生学习的信心.
5.反馈练习,巩固知识 练习一 (1)计算: ①105×106②a7 a3 ③ b5 b ④a6 a6(2)计算: ①x10 x ②10×102×10 第(1)题由学生口答;第(2)题在练习本上完成,然后同桌互阅,教师抽查. 练习一主要是对性质运用的强化,形成定势.
③y4 y3 y2 y④–a2 a6练习二下面的计算对不对?如果不对,应怎样改正?(1)b5 b5=2b5(2)b5+b5=b10 (3)x5 x5=2x10 (4)x5x5=x25 (5)c c3=c3 (6)m+m3=m4 此练习以学生抢答方式完成.注意训练学生的表述能力,以提高兴趣. 练习二中主要是通过学生对题目的观察、比较、判断,提高学生的是非辨别能力.(1)(2)小题强调同底数幂乘法与整式加减的区别.(3)(4)小题强调性质中的“不变”、“相加”.(5)小题强调“c ”表示“c ”的一次幂.
6.变式训练,培养能力 练习三 填空: (1)x5 ( )=x8 (2)a ( )=a6 (3)x x3 ( )=x7(4)xm ( )=x3m(5)xα ( )=xα+β练习四填空:(1)8=2x ,则x=_____ .(2)8×4=2x ,则x= ______ .(3)3×27×9=3x,则x=_____ . 学生思考后回答.学生同桌或前后左右结组研究、讨论,然后完成. 这组题的目的是训练学生的逆向思维能力.此组题旨在增强学生应变能力和解题灵活性.
7.总结、扩展同底数幂相乘,底数____________,指数____________. 由学生说出本节体会最深的是哪些? 在性质中强调“不变”、“相加”.学生谈体会,不仅是对本节知识的再现,同时也培养了学生的口头表达能力和概括总结能力.
8.布置作业1.计算:(必做题)(1)a3·a4; (2)x3·x; (3) 105· 10· 103;(4) x7· x· x12.2.计算:(选做题)(1)x·x3 +x2·x2; (2)y3·y-y·y·y2;(3) 32· 3· 9-3· 34; (4) 103· 10+100· 102.3.思考与拓展:(1)(–x) ·(–x)3 (2)–b·(–b)2 ·b2(3)an - 1 ·(–a)2 (4)(x+2y)2·(2y+x)3
五、教学反思:
