19.2.2菱形的性质[下学期]
文档属性
| 名称 | 19.2.2菱形的性质[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 302.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-05-22 00:00:00 | ||
图片预览


文档简介
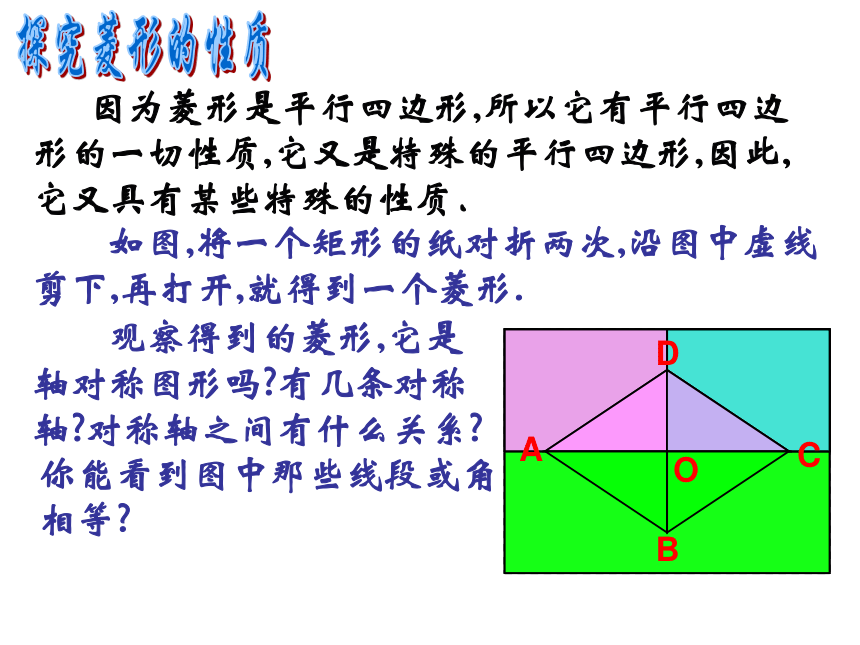
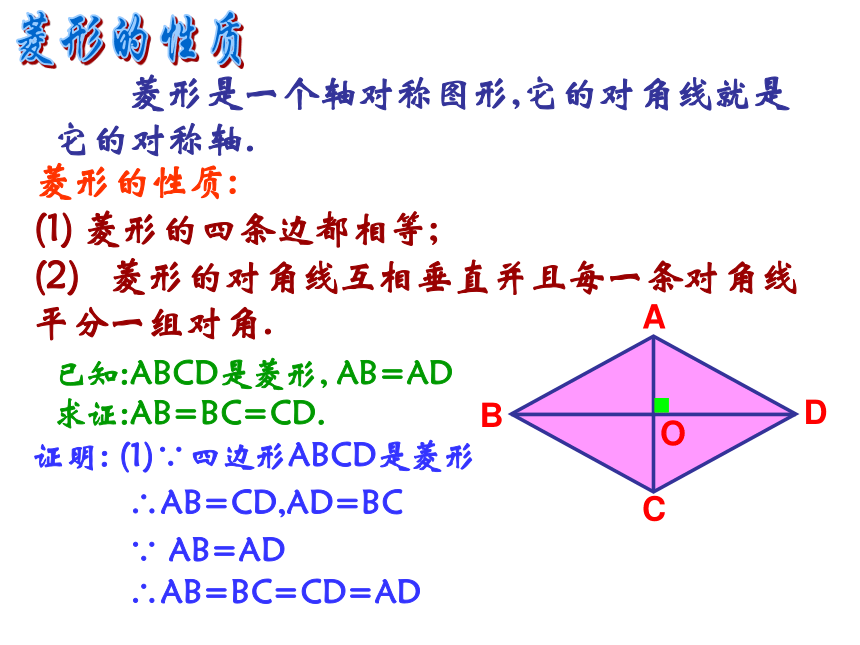
课件15张PPT。第19章 四边形孝感市文昌中学 程世富(19.2.2 特殊的平行四边形---菱形)菱形的定义有一组邻边相等的平行四边形叫做菱形. 定义: 如图,平移平行四边形的一边,使它与相邻的一条边相等,就得到了一个菱形. 菱形在我们的日常生活中也是常见的一种图形.窗格中国结衣帽架装饰材料 如图,将一个矩形的纸对折两次,沿图中虚线剪下,再打开,就得到一个菱形. 观察得到的菱形,它是轴对称图形吗?有几条对称轴?对称轴之间有什么关系?你能看到图中那些线段或角相等?探究菱形的性质ABCDO 因为菱形是平行四边形,所以它有平行四边形的一切性质,它又是特殊的平行四边形,因此,它又具有某些特殊的性质. 菱形的性质(1) 菱形的四条边都相等;(2) 菱形的对角线互相垂直并且每一条对角线平分一组对角. 菱形是一个轴对称图形,它的对角线就是它的对称轴.证明: (1)∵ AB=AD ∴AB=CD,AD=BC 菱形的性质:∵四边形ABCD是菱形∴AB=BC=CD=AD 已知:ABCD是菱形, AB=AD 求证:AB=BC=CD.(2) 菱形的对角线互相垂直并且每一条对角线平分一组对角.已知:菱形ABCD的对角线AC和BD相交于点O,如图,
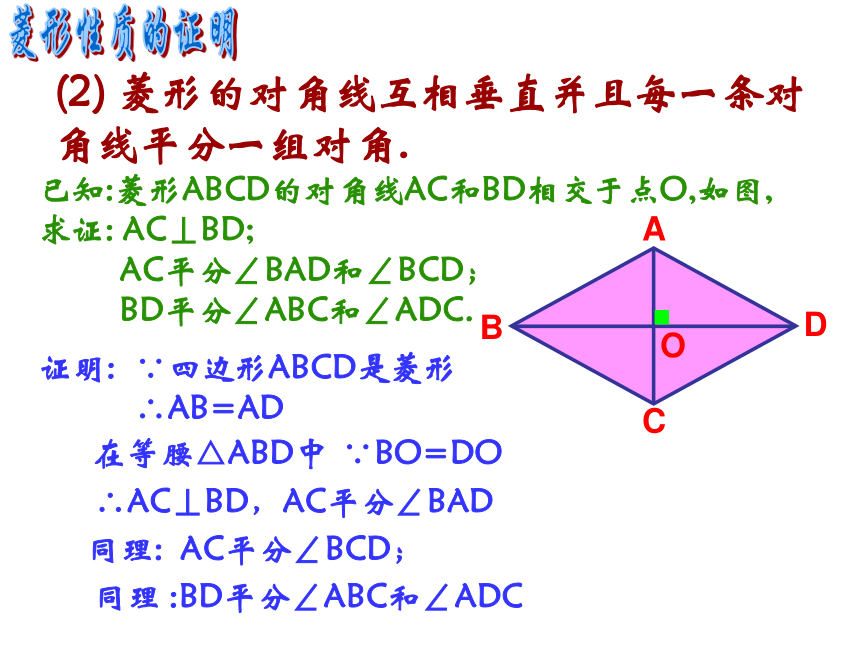
求证: AC⊥BD;
AC平分∠BAD和∠BCD;
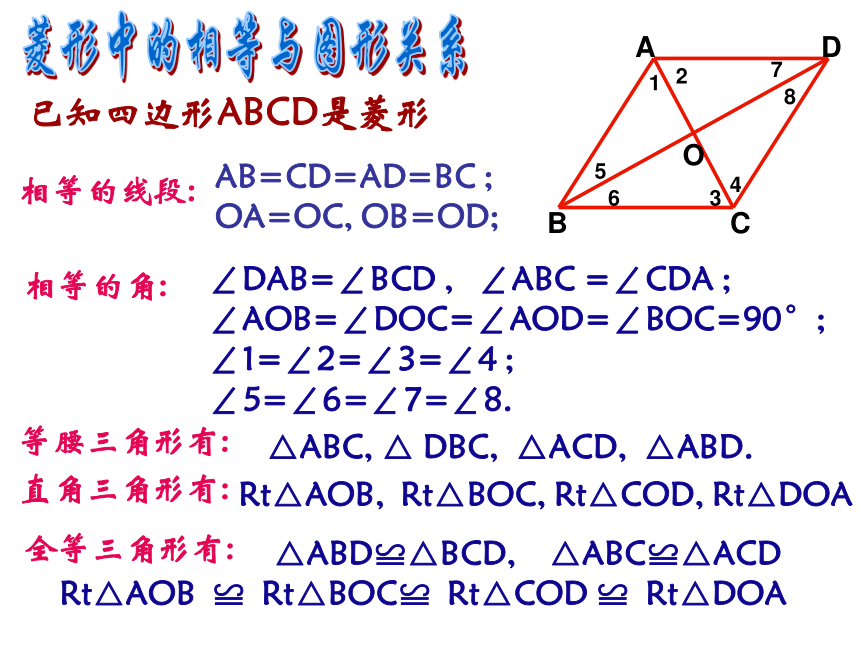
BD平分∠ABC和∠ADC. 证明:∵四边形ABCD是菱形∴AB=AD在等腰△ABD中∵BO=DO∴AC⊥BD,AC平分∠BAD同理: AC平分∠BCD;同理 :BD平分∠ABC和∠ADC菱形性质的证明相等的线段:相等的角:等腰三角形有:直角三角形有:全等三角形有:已知四边形ABCD是菱形AB=CD=AD=BC ; OA=OC, OB=OD;∠DAB=∠BCD , ∠ABC =∠CDA ; ∠AOB=∠DOC=∠AOD=∠BOC=90°; ∠1=∠2=∠3=∠4 ; ∠5=∠6=∠7=∠8.△ABC, △ DBC, △ACD, △ABD.Rt△AOB, Rt△BOC, Rt△COD, Rt△DOA △ABD≌△BCD, △ABC≌△ACD Rt△AOB ≌ Rt△BOC≌ Rt△COD ≌ Rt△DOAABCDO12345678菱形中的相等与图形关系 菱形是特殊的平行四边形,因此可以用平行四边形面积公式来计算菱形的面积, 除此以外,还有计算菱形的面积的方法吗?菱形的面积公式S菱形=S△ABD+S△CBD因此,S菱形=对角线乘积的一半例1. 已知如图,菱形ABCD中,E是AB的中点,且DE⊥AB,AB=1.求: (1)∠ABC的度数; (2)对角线AC、BD的长; (3)菱形ABCD的面积.解: (1) ∵四边形ABCD是菱形∴ AD=AB=1又∵ E为AB中点又∵ DE⊥AB∴ AE=BE=0.5∴ BD=AD=AB=1∴ ∠ABD= 60° 例题∴ BD2=DE2+BE2=DE2+AE2=AD2=1∴△ABD为等边三角形同理 ∠CBD= 60° ∴ ∠ABC= 120° 例1. 已知如图,菱形ABCD中,E是AB的中点,且DE⊥AB,AB=1.求: (1)∠ABC的度数; (2)对角线AC的长; (3)菱形ABCD的面积.解: (2) ∵ AB=BD=1且ABCD为菱形∴ BD⊥AC, OB=0.5在Rt△ABO中,∴ OA=例题∴ OA2=AB2-OB2∴ AC=2OA=(3) ∵ BD=1,AC=∴ S菱形例题例2. 如图,菱形花坛ABCD的边长为20 m, ∠ABC =60°,沿着菱形的对角线修建了两条小路AC和BD,求: 两条小路的长和花坛的面积(分别精确到0.01m和0.01m2) .解: ∵花坛ABCD是菱形∴ AC⊥BDAC=2AO=20 (m)在RtOAB中,AO= AB∴花坛的两条小路长 ∠ABO= ∠ABC= ×60°=30 °∴ BO2=AB2-AO2= ×20=10 (m) =202-102=300 BD=2BO=20 =34.64 (m)花坛的面积S菱形ABCD =4S△OAB∴ BO≈17.32 (m) ≈346.4 (m2) (课本P108/练习)小结有一组邻边相等的平行四边形叫做菱形. 1.菱形的定义:2.菱形的性质:(1) 菱形的四条边都相等;(2) 菱形的对角线互相垂直并且每一条对角线平分一组对角. 菱形是一个轴对称图形,它的对角线就是它的对称轴.S菱形=对角线乘积的一半3.菱形的面积:作业:P113-114习题 19.2/5、11、再见
求证: AC⊥BD;
AC平分∠BAD和∠BCD;
BD平分∠ABC和∠ADC. 证明:∵四边形ABCD是菱形∴AB=AD在等腰△ABD中∵BO=DO∴AC⊥BD,AC平分∠BAD同理: AC平分∠BCD;同理 :BD平分∠ABC和∠ADC菱形性质的证明相等的线段:相等的角:等腰三角形有:直角三角形有:全等三角形有:已知四边形ABCD是菱形AB=CD=AD=BC ; OA=OC, OB=OD;∠DAB=∠BCD , ∠ABC =∠CDA ; ∠AOB=∠DOC=∠AOD=∠BOC=90°; ∠1=∠2=∠3=∠4 ; ∠5=∠6=∠7=∠8.△ABC, △ DBC, △ACD, △ABD.Rt△AOB, Rt△BOC, Rt△COD, Rt△DOA △ABD≌△BCD, △ABC≌△ACD Rt△AOB ≌ Rt△BOC≌ Rt△COD ≌ Rt△DOAABCDO12345678菱形中的相等与图形关系 菱形是特殊的平行四边形,因此可以用平行四边形面积公式来计算菱形的面积, 除此以外,还有计算菱形的面积的方法吗?菱形的面积公式S菱形=S△ABD+S△CBD因此,S菱形=对角线乘积的一半例1. 已知如图,菱形ABCD中,E是AB的中点,且DE⊥AB,AB=1.求: (1)∠ABC的度数; (2)对角线AC、BD的长; (3)菱形ABCD的面积.解: (1) ∵四边形ABCD是菱形∴ AD=AB=1又∵ E为AB中点又∵ DE⊥AB∴ AE=BE=0.5∴ BD=AD=AB=1∴ ∠ABD= 60° 例题∴ BD2=DE2+BE2=DE2+AE2=AD2=1∴△ABD为等边三角形同理 ∠CBD= 60° ∴ ∠ABC= 120° 例1. 已知如图,菱形ABCD中,E是AB的中点,且DE⊥AB,AB=1.求: (1)∠ABC的度数; (2)对角线AC的长; (3)菱形ABCD的面积.解: (2) ∵ AB=BD=1且ABCD为菱形∴ BD⊥AC, OB=0.5在Rt△ABO中,∴ OA=例题∴ OA2=AB2-OB2∴ AC=2OA=(3) ∵ BD=1,AC=∴ S菱形例题例2. 如图,菱形花坛ABCD的边长为20 m, ∠ABC =60°,沿着菱形的对角线修建了两条小路AC和BD,求: 两条小路的长和花坛的面积(分别精确到0.01m和0.01m2) .解: ∵花坛ABCD是菱形∴ AC⊥BDAC=2AO=20 (m)在RtOAB中,AO= AB∴花坛的两条小路长 ∠ABO= ∠ABC= ×60°=30 °∴ BO2=AB2-AO2= ×20=10 (m) =202-102=300 BD=2BO=20 =34.64 (m)花坛的面积S菱形ABCD =4S△OAB∴ BO≈17.32 (m) ≈346.4 (m2) (课本P108/练习)小结有一组邻边相等的平行四边形叫做菱形. 1.菱形的定义:2.菱形的性质:(1) 菱形的四条边都相等;(2) 菱形的对角线互相垂直并且每一条对角线平分一组对角. 菱形是一个轴对称图形,它的对角线就是它的对称轴.S菱形=对角线乘积的一半3.菱形的面积:作业:P113-114习题 19.2/5、11、再见
