矩形的性质[下学期]
图片预览




文档简介
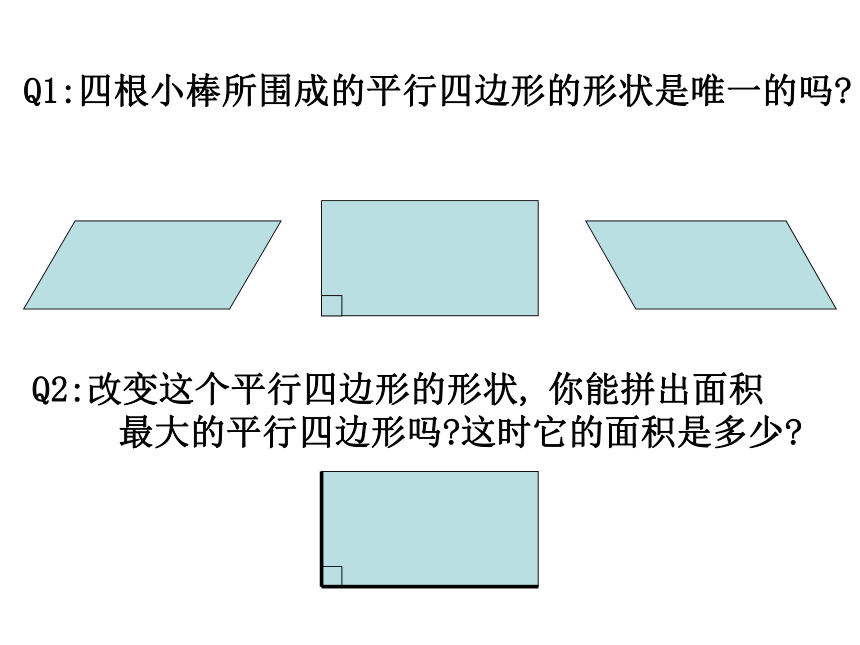
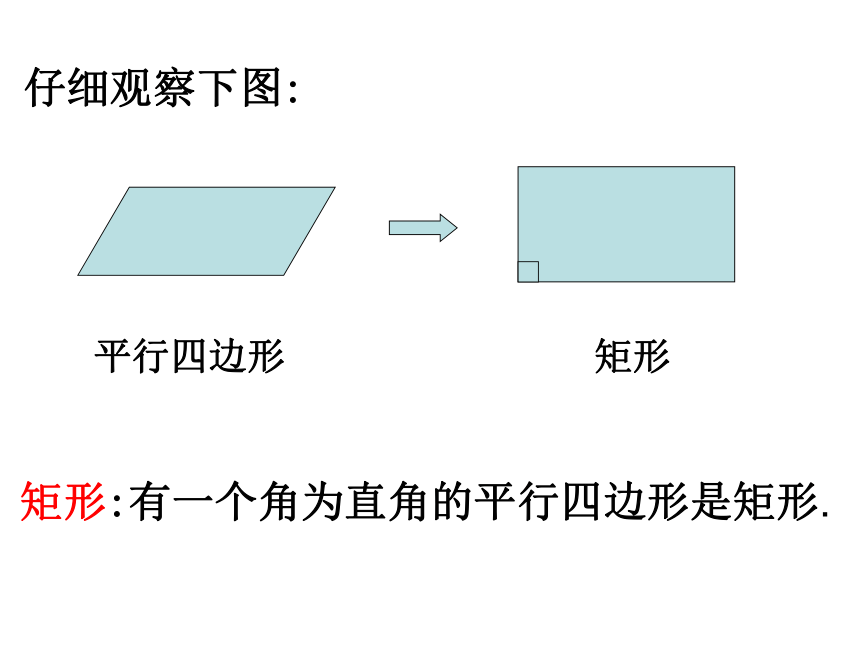
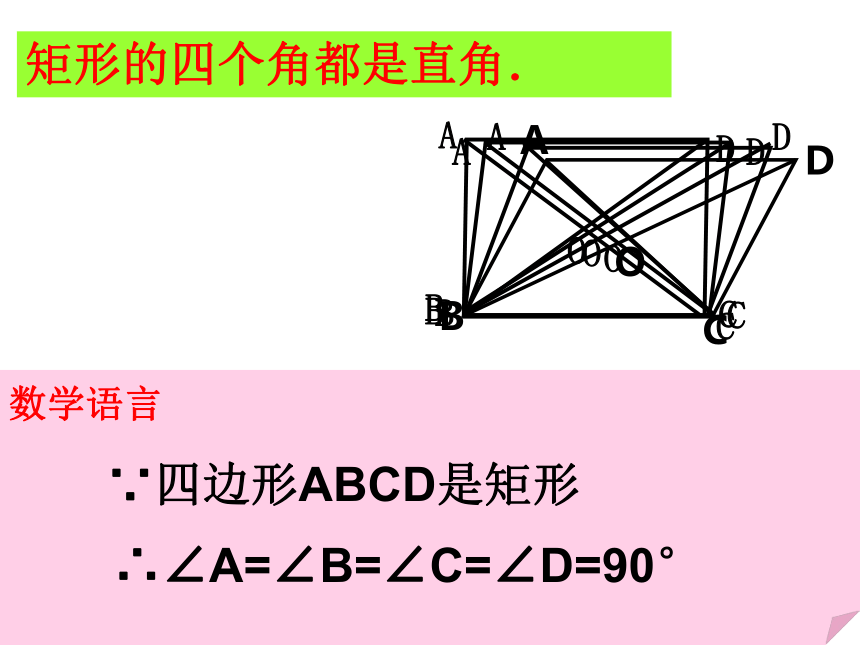
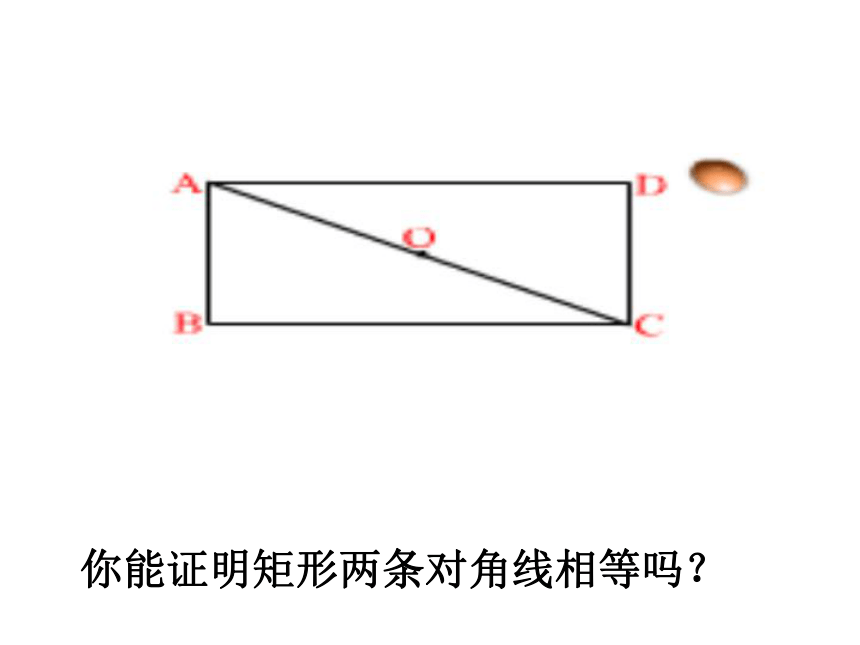
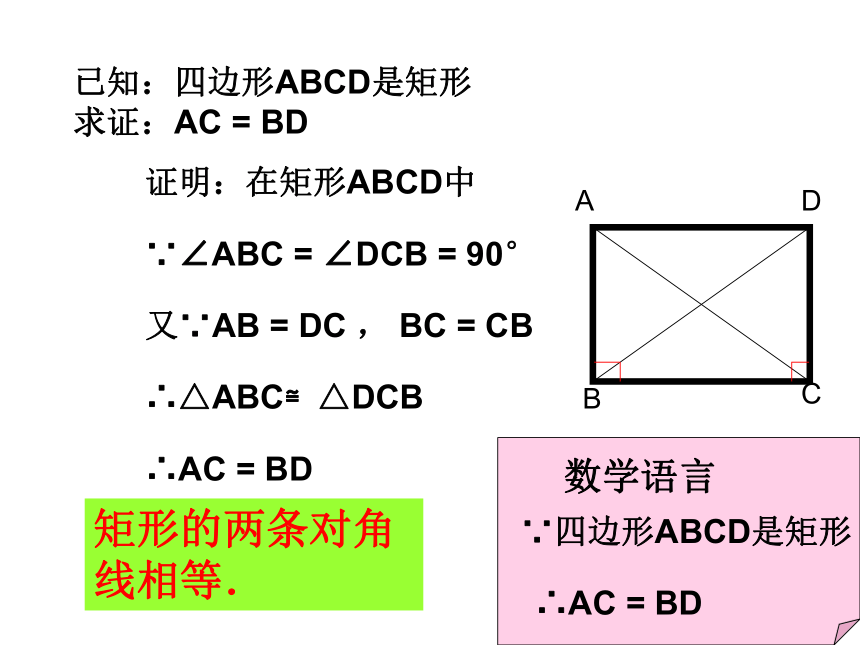
课件26张PPT。19.2.1 矩形矩形的性质Q1:四根小棒所围成的平行四边形的形状是唯一的吗?Q2:改变这个平行四边形的形状, 你能拼出面积 最大的平行四边形吗?这时它的面积是多少?仔细观察下图:平行四边形矩形矩形:有一个角为直角的平行四边形是矩形.生活中的矩形:你能举出一些生活中矩形的例子吗?矩形的四个角都是直角.数学语言∵四边形ABCD是矩形 ∴∠A=∠B=∠C=∠D=90°你能证明矩形两条对角线相等吗?已知:四边形ABCD是矩形
求证:AC = BD证明:在矩形ABCD中∵∠ABC = ∠DCB = 90°又∵AB = DC , BC = CB∴△ABC≌△DCB∴AC = BD矩形的两条对角线相等.数学语言∵四边形ABCD是矩形 ∴AC = BD角边线平行四边形的对角相等.平行四边形的对边平行且相等平行四边形的对角线互相平分矩形的对角相等,均为90度.矩形的对边平行且相等矩形的对角线互相平分且相等对称性中心对称图形角边线对称性中心对称图形,轴对称图形矩形ABCD∠A=∠B=∠C=∠D=90°AC=BDAO=CO=BO=DO在直角三角形中斜边上的中线
等于斜边的一半.ABCDO矩形的对角线把矩形分成四个等腰三角形,其中,相对的两个三角形全等.△AB0是何种三角形?矩形的面积能求吗?解:∵四边形ABCD是矩形.∴AC与BD相等且互相平分(矩形的对角线相等且互相平分)∴OA=OB又∠AOB=60°,∴ △AB0是等边三角形∴OA=AB=4(cm)∴矩形的对角线长AC=BD=2OA=8(cm)变式训练:P104-3.(1)矩形具有而平行四边形不具有的性质( )
(A)内角和是360度(B)对角相等
(C)对边平行且相等(D)对角线相等 (2)下面性质中,矩形不一定具有的是( )
(A)对角线相等(B)四个角相等
(C)是轴对称图形(D)对角线垂直(3)由已知矩形的一个顶点向其所对的对角线引垂线,该垂线分直角为3:1两部分,则垂线与另一条对角线的夹角是( )
(A)50度(B)45度(C)30度(D)22.5度DDB如图,在矩形ABCD中,AC与BD相交于点O,AB=3cm,BC=4cm 则AC= cm,
AO= cm,BO= cm. 52.5 2.54A例2:如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86cm,对角线的长是13cm,那么矩形的周长是多少?在矩形ABCD中,有AD=BC;AB=CD;AC=DB;
AO=OC=OB=OD∴AD+BC+AB+DC+2AC+2BD=86又∵AC=DB=13∴AD+AB+BC+DC=86-52=34(角)(边)(线)矩形的对角相等,均为90度.矩形的对边对平行且相等矩形的对角线互相平分且相等有一个角为直角的平行四边形是矩形本节课你有哪些收获?对角线夹角为60°或120°,其中必有一个等边三角形.本课小结矩形与平行四边形的性质对比两对角线相等且互相平分两条对角线互相平分对角线对角相等,都是90°对角相等角两组对边平行且相等两组对边平行且相等边矩形平行四边形性质开动脑筋 如图,在△ABC中,D,E,F,分别是BC、AC、AB边的中点,AH⊥BC于H,FD=8㎝,则HE=8㎝例1:如图:在矩形ABCD中,两条对角线AC、BD相交于点O, AB=OA=4cm.
求:BD与AD的长
ABOCD随堂练习1. 矩形具有而一般平行四边形不具有的性质是( ).
A 对角线相等 B 对边相等
C 对角相等 D 对角线互相平分 A2.在矩形ABCD中,
AE⊥BD于E,若
BE=OE=1,则
AC= , AB=---BCDEAO423.如图,用8块相同的长方形地砖拼成一个矩形地面,则每块长方形地砖的长和宽分别是( )
(A)48cm,12cm; (B)48cm,16cm;
(C)44cm,16cm; (D)45cm,15cm.D(2).矩形的两条对角线将矩形分成四个面积相等的等腰三角形( )(1).矩形是平行四边形( )4.矩形的短边长为3cm,两对角线所成的角是60 °,则它的另一边长是_______.5. 已知矩形对角线长为4cm,一边长为 cm,
则矩形的面积是________.6.判断题
求证:AC = BD证明:在矩形ABCD中∵∠ABC = ∠DCB = 90°又∵AB = DC , BC = CB∴△ABC≌△DCB∴AC = BD矩形的两条对角线相等.数学语言∵四边形ABCD是矩形 ∴AC = BD角边线平行四边形的对角相等.平行四边形的对边平行且相等平行四边形的对角线互相平分矩形的对角相等,均为90度.矩形的对边平行且相等矩形的对角线互相平分且相等对称性中心对称图形角边线对称性中心对称图形,轴对称图形矩形ABCD∠A=∠B=∠C=∠D=90°AC=BDAO=CO=BO=DO在直角三角形中斜边上的中线
等于斜边的一半.ABCDO矩形的对角线把矩形分成四个等腰三角形,其中,相对的两个三角形全等.△AB0是何种三角形?矩形的面积能求吗?解:∵四边形ABCD是矩形.∴AC与BD相等且互相平分(矩形的对角线相等且互相平分)∴OA=OB又∠AOB=60°,∴ △AB0是等边三角形∴OA=AB=4(cm)∴矩形的对角线长AC=BD=2OA=8(cm)变式训练:P104-3.(1)矩形具有而平行四边形不具有的性质( )
(A)内角和是360度(B)对角相等
(C)对边平行且相等(D)对角线相等 (2)下面性质中,矩形不一定具有的是( )
(A)对角线相等(B)四个角相等
(C)是轴对称图形(D)对角线垂直(3)由已知矩形的一个顶点向其所对的对角线引垂线,该垂线分直角为3:1两部分,则垂线与另一条对角线的夹角是( )
(A)50度(B)45度(C)30度(D)22.5度DDB如图,在矩形ABCD中,AC与BD相交于点O,AB=3cm,BC=4cm 则AC= cm,
AO= cm,BO= cm. 52.5 2.54A例2:如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86cm,对角线的长是13cm,那么矩形的周长是多少?在矩形ABCD中,有AD=BC;AB=CD;AC=DB;
AO=OC=OB=OD∴AD+BC+AB+DC+2AC+2BD=86又∵AC=DB=13∴AD+AB+BC+DC=86-52=34(角)(边)(线)矩形的对角相等,均为90度.矩形的对边对平行且相等矩形的对角线互相平分且相等有一个角为直角的平行四边形是矩形本节课你有哪些收获?对角线夹角为60°或120°,其中必有一个等边三角形.本课小结矩形与平行四边形的性质对比两对角线相等且互相平分两条对角线互相平分对角线对角相等,都是90°对角相等角两组对边平行且相等两组对边平行且相等边矩形平行四边形性质开动脑筋 如图,在△ABC中,D,E,F,分别是BC、AC、AB边的中点,AH⊥BC于H,FD=8㎝,则HE=8㎝例1:如图:在矩形ABCD中,两条对角线AC、BD相交于点O, AB=OA=4cm.
求:BD与AD的长
ABOCD随堂练习1. 矩形具有而一般平行四边形不具有的性质是( ).
A 对角线相等 B 对边相等
C 对角相等 D 对角线互相平分 A2.在矩形ABCD中,
AE⊥BD于E,若
BE=OE=1,则
AC= , AB=---BCDEAO423.如图,用8块相同的长方形地砖拼成一个矩形地面,则每块长方形地砖的长和宽分别是( )
(A)48cm,12cm; (B)48cm,16cm;
(C)44cm,16cm; (D)45cm,15cm.D(2).矩形的两条对角线将矩形分成四个面积相等的等腰三角形( )(1).矩形是平行四边形( )4.矩形的短边长为3cm,两对角线所成的角是60 °,则它的另一边长是_______.5. 已知矩形对角线长为4cm,一边长为 cm,
则矩形的面积是________.6.判断题
