8.3.12×2列联表独立性检验讲义--2022-2023学年高二下学期数学沪教版(2020)选择性必修第二册(含答案)
文档属性
| 名称 | 8.3.12×2列联表独立性检验讲义--2022-2023学年高二下学期数学沪教版(2020)选择性必修第二册(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 254.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 上教版(2020) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-12 20:57:20 | ||
图片预览


文档简介
【学生版】第8 章 成对数据的统计分析 (6课时)
8.3.1 2×2列联表独立性检验
学习目标
1、通过对典型案例的探究,了解独立性检验(只要求2×2列联表)的基本思想;
2、通过对数据的收集、整理和分析,增强学生的社会实践能力;
知识梳理
1、解分类变量与列表;2、理解独立性检验;
巩固练习
一、选择题
1、对于分类变量X与Y的随机变量的值,下列说法正确的是( )
A.越大,“X与Y有关系”的可信程度越小
B.越小,“X与Y有关系”的可信程度越小
C.越接近于0,“X与Y没有关系”的可信程度越小
D.越大,“X与Y没有关系”的可信程度越大
2、下面是一个2×2列联表:
X Y 合计
Y=0 Y=1
X=0 a 21 73
X=1 8 25 33
合计 b 46
则表中a,b处的值分别为( )
A.94,96 B.52,50 C.52,60 D.54,52
二、填空题
3、χ2的大小可以决定是否拒绝原来的统计假设H0,如果χ2值较大,就拒绝H0,即接受两个分类变量________关系.(填“有”或“无”)
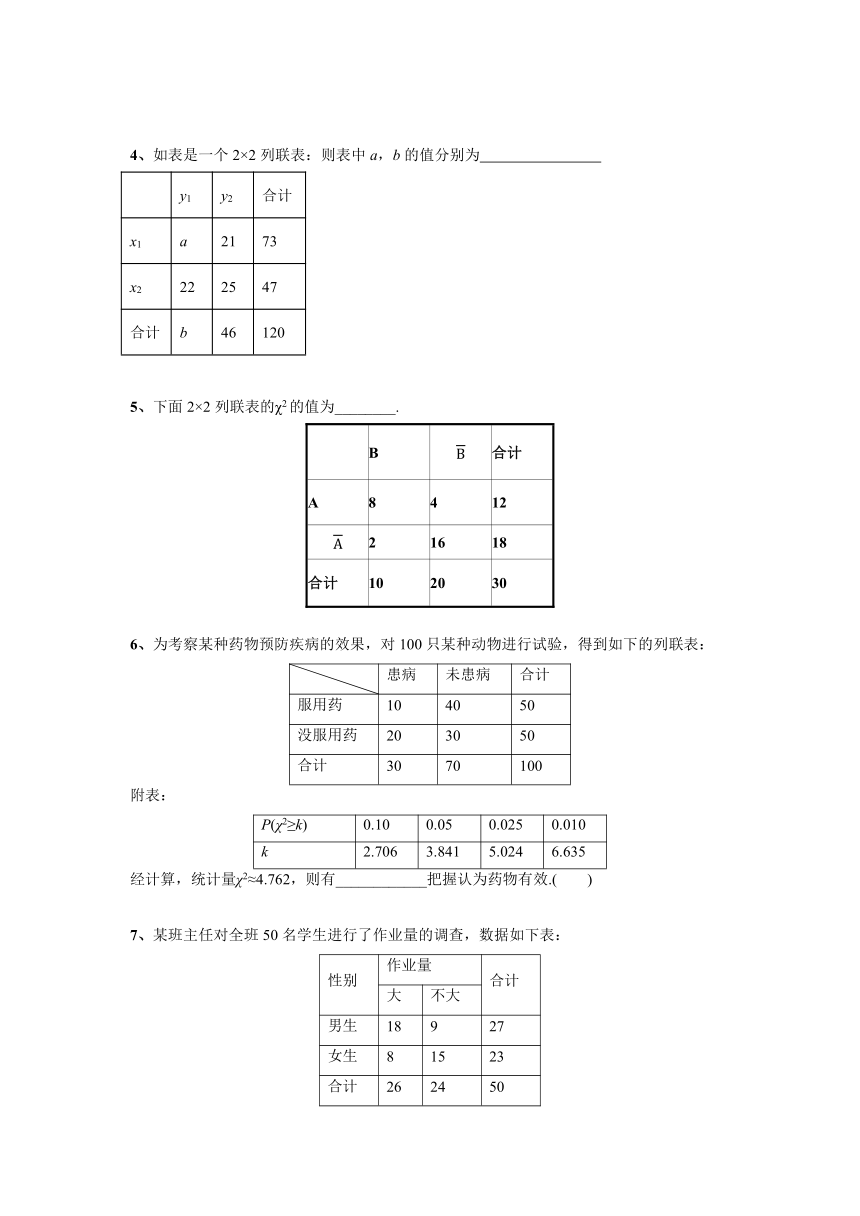
4、如表是一个2×2列联表:则表中a,b的值分别为
y1 y2 合计
x1 a 21 73
x2 22 25 47
合计 b 46 120
5、下面2×2列联表的χ2的值为________.
B 合计
A 8 4 12
2 16 18
合计 10 20 30
6、为考察某种药物预防疾病的效果,对100只某种动物进行试验,得到如下的列联表:
患病 未患病 合计
服用药 10 40 50
没服用药 20 30 50
合计 30 70 100
附表:
P(χ2≥k) 0.10 0.05 0.025 0.010
k 2.706 3.841 5.024 6.635
经计算,统计量χ2≈4.762,则有____________把握认为药物有效.( )
7、某班主任对全班50名学生进行了作业量的调查,数据如下表:
性别 作业量 合计
大 不大
男生 18 9 27
女生 8 15 23
合计 26 24 50
附表:
P(χ2≥k) 0.10 0.05 0.025 0.010
k 2.706 3.841 5.024 6.635
则推断“学生的性别与认为作业量大有关”这种推断犯错误的概率不超过
8、为考察高中生的性别与是否喜欢数学课程之间的关系.利用2×2列联表进行检验.经计算χ2=7.069.参考下表,则认为“性别与是否喜欢数学课程有关”犯错误的概率不超过
P(χ2≥k) 0.100 0.050 0.025 0.010 0.001
k 2.706 3.841 5.024 6.635 10.828
9、某学校为了制订治理学校门口,上学、放学期间家长接送孩子乱停车现象的措施,对全校学生家长进行了问卷调查.根据从中随机抽取的50份调查问卷,得到了如下的2×2列联表:
同意限定区域停车 不同意限定区域停车 合计
男 20 5 25
女 10 15 25
合计 30 20 50
则认为“是否同意限定区域停车与家长的性别有关”的把握约为____________.
10、有两个分类变量和,其中一组观测值为如下的2×2列联表:
总计
15
50
总计 20 45 65
其中,均为大于5的整数,则__________时,在犯错误的概率不超过的前提下为“和之间有关系”;附:
0.15 0.10 0.05 0.025 0.010 0.005 0.001
2.072 2.706 3.841 5.024 6.635 7.879 10.828
三、解答题
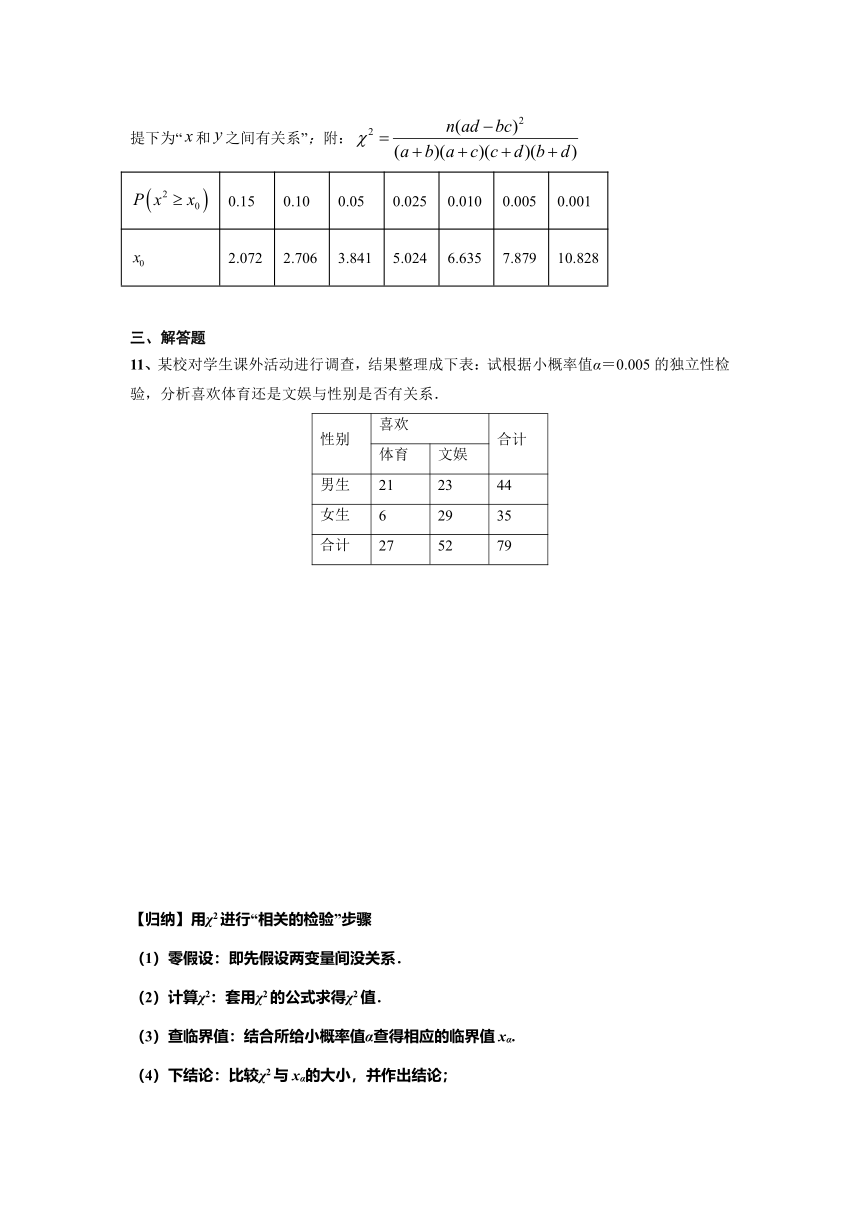
11、某校对学生课外活动进行调查,结果整理成下表:试根据小概率值α=0.005的独立性检验,分析喜欢体育还是文娱与性别是否有关系.
性别 喜欢 合计
体育 文娱
男生 21 23 44
女生 6 29 35
合计 27 52 79
【归纳】用χ2进行“相关的检验”步骤
(1)零假设:即先假设两变量间没关系.
(2)计算χ2:套用χ2的公式求得χ2值.
(3)查临界值:结合所给小概率值α查得相应的临界值xα.
(4)下结论:比较χ2与xα的大小,并作出结论;
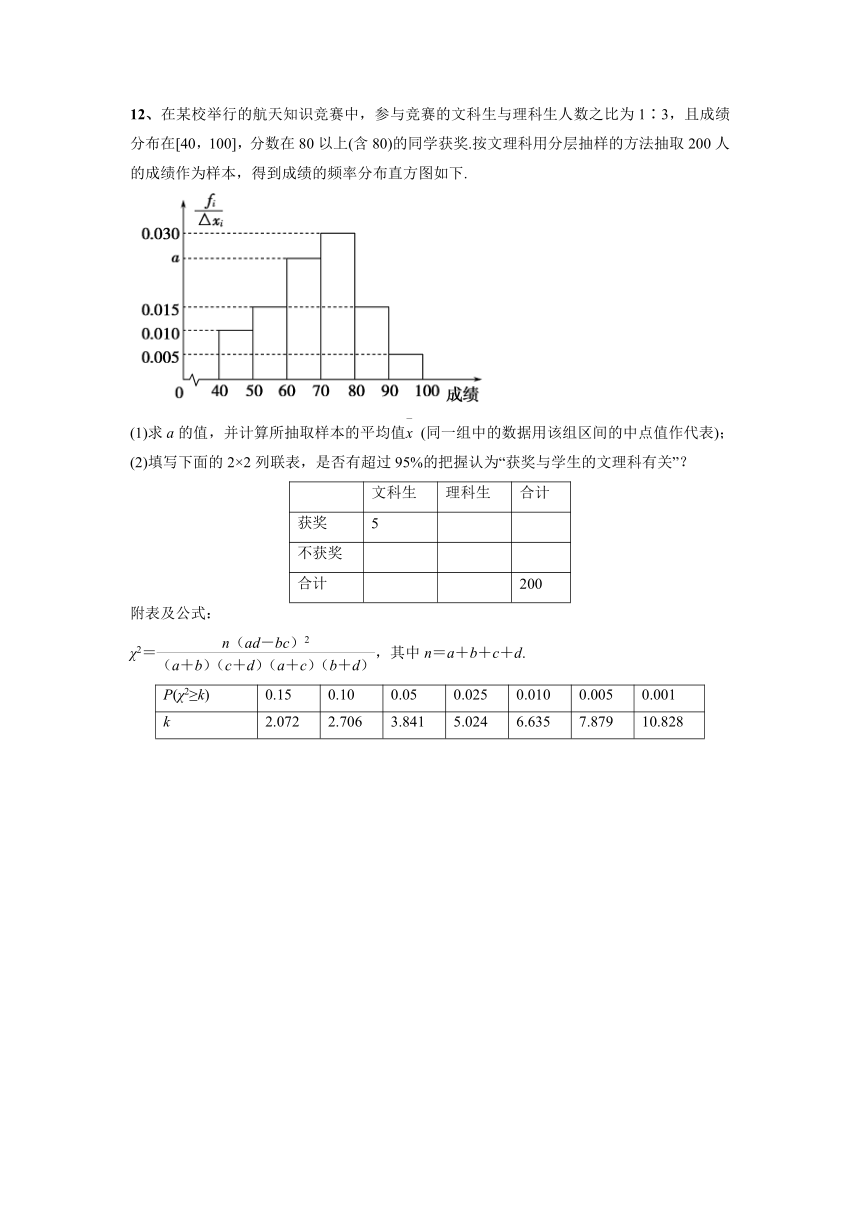
12、在某校举行的航天知识竞赛中,参与竞赛的文科生与理科生人数之比为1∶3,且成绩分布在[40,100],分数在80以上(含80)的同学获奖.按文理科用分层抽样的方法抽取200人的成绩作为样本,得到成绩的频率分布直方图如下.
(1)求a的值,并计算所抽取样本的平均值 (同一组中的数据用该组区间的中点值作代表);
(2)填写下面的2×2列联表,是否有超过95%的把握认为“获奖与学生的文理科有关”?
文科生 理科生 合计
获奖 5
不获奖
合计 200
附表及公式:
χ2=,其中n=a+b+c+d.
P(χ2≥k) 0.15 0.10 0.05 0.025 0.010 0.005 0.001
k 2.072 2.706 3.841 5.024 6.635 7.879 10.828
四、思考题
第24届冬奥会已于2022年在北京市和张家口市联合举行,冬奥会志愿者的服务工作是成功举办的重要保障.在冬奥会的志愿者选拔工作中,某高校承办了冬奥会志愿者选拔的面试工作,面试成绩满分100分,现随机抽取了名候选者的面试成绩分五组,第一组,第二组,第三组,第四组,第五组,绘制成如图所示的频率分布直方图.已知图中从左到右前三个组的频率成等差数列,第一组和第五组的频率相同.
(1)求,的值,并估计这名候选者面试成绩的中位数(中位数精确到0.1);
(2)已知抽取的名候选人中,男生和女生各人,男生希望参加张家口赛区志愿服务的人数有人,女生希望参加张家口赛区志愿服务的人数有人,补全下面列联表,问是否有的把握认为希望参加张家口赛区志愿者服务的候选人与性别有关?
男生 女生 总计
希望去张家口赛区
不希望去张家口赛区
总计
参考数据即公式:,.
0.15 0.10 0.05 0.025 0.010 0.005 0.001
2.072 2.706 3.841 5.024 6.635 7.879 10.828
【教师版】第8 章 成对数据的统计分析 (6课时)
8.3.1 2×2列联表独立性检验
学习目标
1、通过对典型案例的探究,了解独立性检验(只要求2×2列联表)的基本思想;
2、通过对数据的收集、整理和分析,增强学生的社会实践能力;
知识梳理
1、解分类变量与列表;2、理解独立性检验;
巩固练习
一、选择题
1、对于分类变量X与Y的随机变量的值,下列说法正确的是( )
A.越大,“X与Y有关系”的可信程度越小
B.越小,“X与Y有关系”的可信程度越小
C.越接近于0,“X与Y没有关系”的可信程度越小
D.越大,“X与Y没有关系”的可信程度越大
解析:根据独立性检验的基本思想可知,分类变量X与Y的随机变量的观测值越大,“X与Y没有关系”的可信程度越小,则“X与Y有关系”的可信程度越大;越小,“X与Y有关系”的可信程度越小,“X与Y没有关系”的可信程度越大,故ACD错误,B正确.
故选:B;
答案:B;
2、下面是一个2×2列联表:
X Y 合计
Y=0 Y=1
X=0 a 21 73
X=1 8 25 33
合计 b 46
则表中a,b处的值分别为( )
A.94,96 B.52,50 C.52,60 D.54,52
解析:因为,a+21=73,所以,a=52,b=a+8=52+8=60;
答案:C;
二、填空题
3、χ2的大小可以决定是否拒绝原来的统计假设H0,如果χ2值较大,就拒绝H0,即接受两个分类变量________关系.(填“有”或“无”)
答案:有
4、如表是一个2×2列联表:则表中a,b的值分别为
y1 y2 合计
x1 a 21 73
x2 22 25 47
合计 b 46 120
解析:a=73-21=52,b=a+22=52+22=74.
答案:52,74
5、下面2×2列联表的χ2的值为________.
B 合计
A 8 4 12
2 16 18
合计 10 20 30
解析:χ2==10.
答案:10
6、为考察某种药物预防疾病的效果,对100只某种动物进行试验,得到如下的列联表:
患病 未患病 合计
服用药 10 40 50
没服用药 20 30 50
合计 30 70 100
附表:
P(χ2≥k) 0.10 0.05 0.025 0.010
k 2.706 3.841 5.024 6.635
经计算,统计量χ2≈4.762,则有____________把握认为药物有效.( )
解析:因为χ2>3.841,所以有95%的把握认为药物有效.
答案:95%
7、某班主任对全班50名学生进行了作业量的调查,数据如下表:
性别 作业量 合计
大 不大
男生 18 9 27
女生 8 15 23
合计 26 24 50
附表:
P(χ2≥k) 0.10 0.05 0.025 0.010
k 2.706 3.841 5.024 6.635
则推断“学生的性别与认为作业量大有关”这种推断犯错误的概率不超过
解析:由公式得
χ2=≈5.059>3.841=x0.05,所以,犯错误的概率不超过0.05.
答案:0.05
8、为考察高中生的性别与是否喜欢数学课程之间的关系.利用2×2列联表进行检验.经计算χ2=7.069.参考下表,则认为“性别与是否喜欢数学课程有关”犯错误的概率不超过
P(χ2≥k) 0.100 0.050 0.025 0.010 0.001
k 2.706 3.841 5.024 6.635 10.828
解析:k=7.069>6.635,对照表格,则认为“性别与是否喜欢数学课程有关”犯错误的概率不超过0.01;
答案:0.01;
9、某学校为了制订治理学校门口,上学、放学期间家长接送孩子乱停车现象的措施,对全校学生家长进行了问卷调查.根据从中随机抽取的50份调查问卷,得到了如下的2×2列联表:
同意限定区域停车 不同意限定区域停车 合计
男 20 5 25
女 10 15 25
合计 30 20 50
则认为“是否同意限定区域停车与家长的性别有关”的把握约为____________.
解析:因为χ2,又,
所以我们有99.5%的把握认为“是否同意限定区域停车与家长的性别有关”.
答案:99.5%
10、有两个分类变量和,其中一组观测值为如下的2×2列联表:
总计
15
50
总计 20 45 65
其中,均为大于5的整数,则__________时,在犯错误的概率不超过的前提下为“和之间有关系”;附:
0.15 0.10 0.05 0.025 0.010 0.005 0.001
2.072 2.706 3.841 5.024 6.635 7.879 10.828
解析:由题意知:,
则,
解得:或,因为:且,,
综上得:,,所以:.
答案:9;
三、解答题
11、某校对学生课外活动进行调查,结果整理成下表:试根据小概率值α=0.005的独立性检验,分析喜欢体育还是文娱与性别是否有关系.
性别 喜欢 合计
体育 文娱
男生 21 23 44
女生 6 29 35
合计 27 52 79
解析:零假设为H0:喜欢体育还是喜欢文娱与性别没有关系.
因为,a=21,b=23,c=6,d=29,n=79,
所以,≈8.106>7.879=x0.005.
根据小概率值α=0.005的独立性检验,我们推断H0不成立,即认为喜欢体育还是喜欢文娱与性别有关;
【归纳】用χ2进行“相关的检验”步骤
(1)零假设:即先假设两变量间没关系.
(2)计算χ2:套用χ2的公式求得χ2值.
(3)查临界值:结合所给小概率值α查得相应的临界值xα.
(4)下结论:比较χ2与xα的大小,并作出结论;
12、在某校举行的航天知识竞赛中,参与竞赛的文科生与理科生人数之比为1∶3,且成绩分布在[40,100],分数在80以上(含80)的同学获奖.按文理科用分层抽样的方法抽取200人的成绩作为样本,得到成绩的频率分布直方图如下.
(1)求a的值,并计算所抽取样本的平均值 (同一组中的数据用该组区间的中点值作代表);
(2)填写下面的2×2列联表,是否有超过95%的把握认为“获奖与学生的文理科有关”?
文科生 理科生 合计
获奖 5
不获奖
合计 200
附表及公式:
χ2=,其中n=a+b+c+d.
P(χ2≥k) 0.15 0.10 0.05 0.025 0.010 0.005 0.001
k 2.072 2.706 3.841 5.024 6.635 7.879 10.828
解析:(1)由频率分布直方图,
可得a=[1-(0.01+0.015+0.03+0.015+0.005)×10]÷10=0.025,
=45×0.1+55×0.15+65×0.25+75×0.3+85×0.15+95×0.05=69.
(2)填写2×2列联表如下:
文科生 理科生 合计
获奖 5 35 40
不获奖 45 115 160
合计 50 150 200
则χ2==≈4.167>3.841,
所以,有超过95%的把握认为“获奖与学生的文理科有关”.
四、思考题
第24届冬奥会已于2022年在北京市和张家口市联合举行,冬奥会志愿者的服务工作是成功举办的重要保障.在冬奥会的志愿者选拔工作中,某高校承办了冬奥会志愿者选拔的面试工作,面试成绩满分100分,现随机抽取了名候选者的面试成绩分五组,第一组,第二组,第三组,第四组,第五组,绘制成如图所示的频率分布直方图.已知图中从左到右前三个组的频率成等差数列,第一组和第五组的频率相同.
(1)求,的值,并估计这名候选者面试成绩的中位数(中位数精确到0.1);
(2)已知抽取的名候选人中,男生和女生各人,男生希望参加张家口赛区志愿服务的人数有人,女生希望参加张家口赛区志愿服务的人数有人,补全下面列联表,问是否有的把握认为希望参加张家口赛区志愿者服务的候选人与性别有关?
男生 女生 总计
希望去张家口赛区
不希望去张家口赛区
总计
参考数据即公式:,.
0.15 0.10 0.05 0.025 0.010 0.005 0.001
2.072 2.706 3.841 5.024 6.635 7.879 10.828
解析:(1)由题意可知:,,
解得,,所以中位数等于
(2)补全列联表:
男生 女生 总计
希望去张家口赛区
不希望去张家口赛区
总计
所以有的把握认为希望参加张家口赛区志愿者服务的候选人与性别有关.
8.3.1 2×2列联表独立性检验
学习目标
1、通过对典型案例的探究,了解独立性检验(只要求2×2列联表)的基本思想;
2、通过对数据的收集、整理和分析,增强学生的社会实践能力;
知识梳理
1、解分类变量与列表;2、理解独立性检验;
巩固练习
一、选择题
1、对于分类变量X与Y的随机变量的值,下列说法正确的是( )
A.越大,“X与Y有关系”的可信程度越小
B.越小,“X与Y有关系”的可信程度越小
C.越接近于0,“X与Y没有关系”的可信程度越小
D.越大,“X与Y没有关系”的可信程度越大
2、下面是一个2×2列联表:
X Y 合计
Y=0 Y=1
X=0 a 21 73
X=1 8 25 33
合计 b 46
则表中a,b处的值分别为( )
A.94,96 B.52,50 C.52,60 D.54,52
二、填空题
3、χ2的大小可以决定是否拒绝原来的统计假设H0,如果χ2值较大,就拒绝H0,即接受两个分类变量________关系.(填“有”或“无”)
4、如表是一个2×2列联表:则表中a,b的值分别为
y1 y2 合计
x1 a 21 73
x2 22 25 47
合计 b 46 120
5、下面2×2列联表的χ2的值为________.
B 合计
A 8 4 12
2 16 18
合计 10 20 30
6、为考察某种药物预防疾病的效果,对100只某种动物进行试验,得到如下的列联表:
患病 未患病 合计
服用药 10 40 50
没服用药 20 30 50
合计 30 70 100
附表:
P(χ2≥k) 0.10 0.05 0.025 0.010
k 2.706 3.841 5.024 6.635
经计算,统计量χ2≈4.762,则有____________把握认为药物有效.( )
7、某班主任对全班50名学生进行了作业量的调查,数据如下表:
性别 作业量 合计
大 不大
男生 18 9 27
女生 8 15 23
合计 26 24 50
附表:
P(χ2≥k) 0.10 0.05 0.025 0.010
k 2.706 3.841 5.024 6.635
则推断“学生的性别与认为作业量大有关”这种推断犯错误的概率不超过
8、为考察高中生的性别与是否喜欢数学课程之间的关系.利用2×2列联表进行检验.经计算χ2=7.069.参考下表,则认为“性别与是否喜欢数学课程有关”犯错误的概率不超过
P(χ2≥k) 0.100 0.050 0.025 0.010 0.001
k 2.706 3.841 5.024 6.635 10.828
9、某学校为了制订治理学校门口,上学、放学期间家长接送孩子乱停车现象的措施,对全校学生家长进行了问卷调查.根据从中随机抽取的50份调查问卷,得到了如下的2×2列联表:
同意限定区域停车 不同意限定区域停车 合计
男 20 5 25
女 10 15 25
合计 30 20 50
则认为“是否同意限定区域停车与家长的性别有关”的把握约为____________.
10、有两个分类变量和,其中一组观测值为如下的2×2列联表:
总计
15
50
总计 20 45 65
其中,均为大于5的整数,则__________时,在犯错误的概率不超过的前提下为“和之间有关系”;附:
0.15 0.10 0.05 0.025 0.010 0.005 0.001
2.072 2.706 3.841 5.024 6.635 7.879 10.828
三、解答题
11、某校对学生课外活动进行调查,结果整理成下表:试根据小概率值α=0.005的独立性检验,分析喜欢体育还是文娱与性别是否有关系.
性别 喜欢 合计
体育 文娱
男生 21 23 44
女生 6 29 35
合计 27 52 79
【归纳】用χ2进行“相关的检验”步骤
(1)零假设:即先假设两变量间没关系.
(2)计算χ2:套用χ2的公式求得χ2值.
(3)查临界值:结合所给小概率值α查得相应的临界值xα.
(4)下结论:比较χ2与xα的大小,并作出结论;
12、在某校举行的航天知识竞赛中,参与竞赛的文科生与理科生人数之比为1∶3,且成绩分布在[40,100],分数在80以上(含80)的同学获奖.按文理科用分层抽样的方法抽取200人的成绩作为样本,得到成绩的频率分布直方图如下.
(1)求a的值,并计算所抽取样本的平均值 (同一组中的数据用该组区间的中点值作代表);
(2)填写下面的2×2列联表,是否有超过95%的把握认为“获奖与学生的文理科有关”?
文科生 理科生 合计
获奖 5
不获奖
合计 200
附表及公式:
χ2=,其中n=a+b+c+d.
P(χ2≥k) 0.15 0.10 0.05 0.025 0.010 0.005 0.001
k 2.072 2.706 3.841 5.024 6.635 7.879 10.828
四、思考题
第24届冬奥会已于2022年在北京市和张家口市联合举行,冬奥会志愿者的服务工作是成功举办的重要保障.在冬奥会的志愿者选拔工作中,某高校承办了冬奥会志愿者选拔的面试工作,面试成绩满分100分,现随机抽取了名候选者的面试成绩分五组,第一组,第二组,第三组,第四组,第五组,绘制成如图所示的频率分布直方图.已知图中从左到右前三个组的频率成等差数列,第一组和第五组的频率相同.
(1)求,的值,并估计这名候选者面试成绩的中位数(中位数精确到0.1);
(2)已知抽取的名候选人中,男生和女生各人,男生希望参加张家口赛区志愿服务的人数有人,女生希望参加张家口赛区志愿服务的人数有人,补全下面列联表,问是否有的把握认为希望参加张家口赛区志愿者服务的候选人与性别有关?
男生 女生 总计
希望去张家口赛区
不希望去张家口赛区
总计
参考数据即公式:,.
0.15 0.10 0.05 0.025 0.010 0.005 0.001
2.072 2.706 3.841 5.024 6.635 7.879 10.828
【教师版】第8 章 成对数据的统计分析 (6课时)
8.3.1 2×2列联表独立性检验
学习目标
1、通过对典型案例的探究,了解独立性检验(只要求2×2列联表)的基本思想;
2、通过对数据的收集、整理和分析,增强学生的社会实践能力;
知识梳理
1、解分类变量与列表;2、理解独立性检验;
巩固练习
一、选择题
1、对于分类变量X与Y的随机变量的值,下列说法正确的是( )
A.越大,“X与Y有关系”的可信程度越小
B.越小,“X与Y有关系”的可信程度越小
C.越接近于0,“X与Y没有关系”的可信程度越小
D.越大,“X与Y没有关系”的可信程度越大
解析:根据独立性检验的基本思想可知,分类变量X与Y的随机变量的观测值越大,“X与Y没有关系”的可信程度越小,则“X与Y有关系”的可信程度越大;越小,“X与Y有关系”的可信程度越小,“X与Y没有关系”的可信程度越大,故ACD错误,B正确.
故选:B;
答案:B;
2、下面是一个2×2列联表:
X Y 合计
Y=0 Y=1
X=0 a 21 73
X=1 8 25 33
合计 b 46
则表中a,b处的值分别为( )
A.94,96 B.52,50 C.52,60 D.54,52
解析:因为,a+21=73,所以,a=52,b=a+8=52+8=60;
答案:C;
二、填空题
3、χ2的大小可以决定是否拒绝原来的统计假设H0,如果χ2值较大,就拒绝H0,即接受两个分类变量________关系.(填“有”或“无”)
答案:有
4、如表是一个2×2列联表:则表中a,b的值分别为
y1 y2 合计
x1 a 21 73
x2 22 25 47
合计 b 46 120
解析:a=73-21=52,b=a+22=52+22=74.
答案:52,74
5、下面2×2列联表的χ2的值为________.
B 合计
A 8 4 12
2 16 18
合计 10 20 30
解析:χ2==10.
答案:10
6、为考察某种药物预防疾病的效果,对100只某种动物进行试验,得到如下的列联表:
患病 未患病 合计
服用药 10 40 50
没服用药 20 30 50
合计 30 70 100
附表:
P(χ2≥k) 0.10 0.05 0.025 0.010
k 2.706 3.841 5.024 6.635
经计算,统计量χ2≈4.762,则有____________把握认为药物有效.( )
解析:因为χ2>3.841,所以有95%的把握认为药物有效.
答案:95%
7、某班主任对全班50名学生进行了作业量的调查,数据如下表:
性别 作业量 合计
大 不大
男生 18 9 27
女生 8 15 23
合计 26 24 50
附表:
P(χ2≥k) 0.10 0.05 0.025 0.010
k 2.706 3.841 5.024 6.635
则推断“学生的性别与认为作业量大有关”这种推断犯错误的概率不超过
解析:由公式得
χ2=≈5.059>3.841=x0.05,所以,犯错误的概率不超过0.05.
答案:0.05
8、为考察高中生的性别与是否喜欢数学课程之间的关系.利用2×2列联表进行检验.经计算χ2=7.069.参考下表,则认为“性别与是否喜欢数学课程有关”犯错误的概率不超过
P(χ2≥k) 0.100 0.050 0.025 0.010 0.001
k 2.706 3.841 5.024 6.635 10.828
解析:k=7.069>6.635,对照表格,则认为“性别与是否喜欢数学课程有关”犯错误的概率不超过0.01;
答案:0.01;
9、某学校为了制订治理学校门口,上学、放学期间家长接送孩子乱停车现象的措施,对全校学生家长进行了问卷调查.根据从中随机抽取的50份调查问卷,得到了如下的2×2列联表:
同意限定区域停车 不同意限定区域停车 合计
男 20 5 25
女 10 15 25
合计 30 20 50
则认为“是否同意限定区域停车与家长的性别有关”的把握约为____________.
解析:因为χ2,又,
所以我们有99.5%的把握认为“是否同意限定区域停车与家长的性别有关”.
答案:99.5%
10、有两个分类变量和,其中一组观测值为如下的2×2列联表:
总计
15
50
总计 20 45 65
其中,均为大于5的整数,则__________时,在犯错误的概率不超过的前提下为“和之间有关系”;附:
0.15 0.10 0.05 0.025 0.010 0.005 0.001
2.072 2.706 3.841 5.024 6.635 7.879 10.828
解析:由题意知:,
则,
解得:或,因为:且,,
综上得:,,所以:.
答案:9;
三、解答题
11、某校对学生课外活动进行调查,结果整理成下表:试根据小概率值α=0.005的独立性检验,分析喜欢体育还是文娱与性别是否有关系.
性别 喜欢 合计
体育 文娱
男生 21 23 44
女生 6 29 35
合计 27 52 79
解析:零假设为H0:喜欢体育还是喜欢文娱与性别没有关系.
因为,a=21,b=23,c=6,d=29,n=79,
所以,≈8.106>7.879=x0.005.
根据小概率值α=0.005的独立性检验,我们推断H0不成立,即认为喜欢体育还是喜欢文娱与性别有关;
【归纳】用χ2进行“相关的检验”步骤
(1)零假设:即先假设两变量间没关系.
(2)计算χ2:套用χ2的公式求得χ2值.
(3)查临界值:结合所给小概率值α查得相应的临界值xα.
(4)下结论:比较χ2与xα的大小,并作出结论;
12、在某校举行的航天知识竞赛中,参与竞赛的文科生与理科生人数之比为1∶3,且成绩分布在[40,100],分数在80以上(含80)的同学获奖.按文理科用分层抽样的方法抽取200人的成绩作为样本,得到成绩的频率分布直方图如下.
(1)求a的值,并计算所抽取样本的平均值 (同一组中的数据用该组区间的中点值作代表);
(2)填写下面的2×2列联表,是否有超过95%的把握认为“获奖与学生的文理科有关”?
文科生 理科生 合计
获奖 5
不获奖
合计 200
附表及公式:
χ2=,其中n=a+b+c+d.
P(χ2≥k) 0.15 0.10 0.05 0.025 0.010 0.005 0.001
k 2.072 2.706 3.841 5.024 6.635 7.879 10.828
解析:(1)由频率分布直方图,
可得a=[1-(0.01+0.015+0.03+0.015+0.005)×10]÷10=0.025,
=45×0.1+55×0.15+65×0.25+75×0.3+85×0.15+95×0.05=69.
(2)填写2×2列联表如下:
文科生 理科生 合计
获奖 5 35 40
不获奖 45 115 160
合计 50 150 200
则χ2==≈4.167>3.841,
所以,有超过95%的把握认为“获奖与学生的文理科有关”.
四、思考题
第24届冬奥会已于2022年在北京市和张家口市联合举行,冬奥会志愿者的服务工作是成功举办的重要保障.在冬奥会的志愿者选拔工作中,某高校承办了冬奥会志愿者选拔的面试工作,面试成绩满分100分,现随机抽取了名候选者的面试成绩分五组,第一组,第二组,第三组,第四组,第五组,绘制成如图所示的频率分布直方图.已知图中从左到右前三个组的频率成等差数列,第一组和第五组的频率相同.
(1)求,的值,并估计这名候选者面试成绩的中位数(中位数精确到0.1);
(2)已知抽取的名候选人中,男生和女生各人,男生希望参加张家口赛区志愿服务的人数有人,女生希望参加张家口赛区志愿服务的人数有人,补全下面列联表,问是否有的把握认为希望参加张家口赛区志愿者服务的候选人与性别有关?
男生 女生 总计
希望去张家口赛区
不希望去张家口赛区
总计
参考数据即公式:,.
0.15 0.10 0.05 0.025 0.010 0.005 0.001
2.072 2.706 3.841 5.024 6.635 7.879 10.828
解析:(1)由题意可知:,,
解得,,所以中位数等于
(2)补全列联表:
男生 女生 总计
希望去张家口赛区
不希望去张家口赛区
总计
所以有的把握认为希望参加张家口赛区志愿者服务的候选人与性别有关.
同课章节目录
